A rigid-flexible coupling finite element model of coupler for analyzing train instability behavior during collision

Jingke Zhang · Tao Zhu · Bing Yang · Xiaorui Wang · Shoune Xiao · Guangwu Yang · Yanwen Liu,2 ·Quanwei Che

Abstract Rail vehicles generate huge longitudinal impact loads in collisions.If unreasonable matching exists between the compressive strength of the intermediate coupler and the structural strength of the car body, the risk of car body structure damage and train derailment will increase.Herein, a four-stage rigid-flexible coupling finite element model of the coupler is established considering the coupler buckling load.The influence of the coupler buckling load on the train longitudinal-vertical-horizontal buckling behavior was studied, and the mechanism of the train horizontal buckling instability in train collisions was revealed.Analysis results show that an intermediate coupler should be designed to ensure that the actual buckling load is less than the compressive load when the car body structure begins to deform plastically.The actual buckling load of the coupler and the asymmetry of the structural strength of the car body in the lateral direction are two important influencing factors for the lateral buckling of a train collision.If the strength of the two sides of the car body structure in the lateral direction is asymmetrical, the deformation on the weaker side will be larger, and the end of the car body will begin to deflect under the action of the coupler force, which in turn causes the train to undergo sawtooth buckling.

Keywords Intermediate coupler · Rigid-flexible coupling finite element model · Design buckling load · Actual buckling load · Lateral buckling instability

1 Introduction

In a train collision, a multistage energy-absorption system can significantly reduce the risk of vehicle damage and derailment [1].The intermediate coupler between rail vehicles is an important part of a multistage energy-absorption system.During normal train operation or collision, the impact force between the front and rear vehicles is primarily transmitted to the coupler mounting base through the coupler.To avoid local buckling of the car body, the maximum load on the coupler system after the maximum compression stroke cannot exceed the maximum load bearing capacity of the non-deformed area of the car body structure.

The existing static strength and crashworthiness standards [2-6] propose specific requirements for the longitudinal strength of the car body and the maximum load on the coupler system (the load of the head coupler shearing and moving backward), as shown in Table 1.However, in independent crashworthiness standards, such as EN 15227:2020,no specific provisions are provided for the dynamic performance of the coupler, and only minimum values for coupler strength are required.Therefore, it is particularly important to explore the relationship between the coupler and car body structure strength.

To simulate the collision instability of a coupler with a collapse tube, previous studies have established a theoretical model [7], multi-body dynamic models [8-11], and a rigid-flexible coupling finite element model (RFCFEM) [12]of the coupler considering only the buffer compression stage[13-16], collapse-tube collapsing stage [17-19], and rigid impact stage.Hence, the models are all three-stage coupler simulation models, in which the authors have not consideredthe instability stage after compressing the intermediate coupler to the maximum stroke.

Table 1 Coupler and car body strength requirements in each standard

Generally, the finite element model (FEM) of the coupler is established using the 6-DOF (degree of freedom)discrete beam element and mat119 material model in LSDYNA software.It can accurately simulate the longitudinal energy absorption and failure behavior of a coupler when overloaded [12].The combined use of a nonlinear torsion spring and spherical joint elements can simulate the pitch and yaw motion characteristics of the coupler device [17],and parameter optimization is common in various aspects of train-crash energy management [20, 21].The existing RFCFEMs for intermediate couplers mainly simulate the buffer compression and collapse phases of the collapse tube.However, they cannot simulate the instability phase after compressing the coupler to its maximum stroke.

As the impact force of the coupler acts directly on the car body structure, when the coupler force exceeds the maximum load that can be withstood by the car body structure, the structure undergoes local buckling deformation, leading to structural damage and train instability.For example, Bounds et al.[22] observed that a high axial force generates a large pitch moment, while a collision off-set or asymmetry of the vehicle structural strength causes a lateral offset of the coupler-force action line from the center of gravity of the vehicle, thus generating a yaw moment.These pitch and yaw moments are sufficient to lift the wheelset offthe rail, but the derailment risk can be reduced by limiting the coupler axial load.Jackiewicz[23] found that the longitudinal impact force generated during traction and braking of a train reduces the durability of the weak structure of the car body.In addition,in the train rescue condition, a large coupler force may be generated owing to longitudinal impact that damages the mechanical structure of the coupler.The coupler attitude and compression displacement significantly influence the lateral stability of the train [24].If the coupler has a pitch angle, the longitudinal compression force generated by braking generates a vertical force, which may further cause the car body to pitch, and the wheels may lift offthe rail.Simultaneously, the vertical force causes local plastic deformation of the car body [25, 26].Therefore,when designing an intermediate coupler, the strength of the car body structure should be considered in addition to the function of the coupler itself, to avoid local or lateral buckling during train collision owing to excessive stiffness and strength of the coupler.

Previously, a collision simulation model [17] of the coupler simulated the pitch, yaw, and longitudinal energyabsorption characteristics accurately within the allowable compression stroke.As an elastic-plastic rod system, after being compressed to the maximum stroke, the intermediate coupler exhibits compressive instability under the action of the longitudinal impact force.However, in the three-stage intermediate coupler model, after the coupler reaches the maximum compression stroke, the longitudinal impact force increases linearly, which cannot reflect the coupler buckling load.Therefore, it is necessary to establish a coupler model that considers the instability characteristics, in order to effectively improve the accuracy of the train collision simulation model.In addition, the mismatch between the coupler strength and car body structure strength may lead to plastic deformation of the car body structure and train derailment in a collision.Therefore, it is necessary to study the matching design of the intermediate coupler and car body structure based on such models.

This study aims to establish a four-stage RFCFEM of the coupler and reveal the mechanism of lateral buckling instability during a train collision from the perspective of the coupler buckling load and body structure strength.Additionally, we propose design elements for the coupler compression strength and car body structure crashworthiness.The main contributions of this study are as follows.

(1) A four-stage RFCFEM is established by combining the longitudinal crush characteristics of the refined finite element model, and a third-stage stiffness calculation method is proposed.

(2) The effects of different coupler buckling loads on train collision instability are investigated, and the mechanism of lateral buckling instability in train collisions is revealed.

(3) Suggestions for crashworthiness design are proposed in terms of the coupler buckling load and the structural strength of the car body.

The remainder of this paper is organized as follows.In Sect.2, we establish the refined finite element model(RFEM) and the four-stage RFCFEM.In Sect.3, a train collision finite element model is presented and four different coupler buckling loads are applied.In Sect.4, the effects of different coupler buckling loads on the longitudinal-vertical-horizontal buckling behavior of the train are analyzed.In Sect.5, conclusions are presented.

2 Finite element model of coupler

2.1 Refined finite element model of coupler

In Ref.[27], the authors established a refined finite element model (RFEM) of the coupler, which is widely used in trains.The model is shown in Figure 1.The accuracy of the model was verified using impact experiments with an intermediate coupler.Compared to the test results, the difference of the model with respect to the initial crush load, maximum longitudinal compressive displacement, minimum compressive load and the maximum compressive load was 6.54%,1.3%, 3.55%, and 6.51%, respectively.The RFEM comprised the following four subsystems: (1) a buffer, (2) connecting snap rings, (3) an expandable collapse tube assembly, and(4) rotary mechanisms.In this model, drawbar A, drawbar B, the expandable collapse tube assembly, and the rubber of the rotary mechanism were considered as deformable parts,which were modeled using an elastic-plastic finite element model.The buffer shell, connecting snap ring, and coupler mounting seat were considered as non-deformable parts and were modeled using a multi-rigid-body finite element model.

In Ref.[27], we investigated the instability behavior of the intermediate coupler under different loading conditions.Buckling instability occurred when the coupler was compressed to its maximum compression stroke.

Although the RFEM of the coupler can better reflect its elastic-plastic deformation behavior, the modeling process is complex.Therefore, in a train collision simulation analysis, generally, a rigid-flexible coupling finite element model(RFCFEM) of the coupler is developed.Currently, the threestage RFCFEM is primarily used, which cannot consider the buckling load of the coupler.A new RFCFEM must reflect the unstable behavior of the coupler.Therefore, a four-stage RFCFEM is proposed in this study.

Reference [27] focused on the instability behavior of the intermediate coupler.This study focuses on the effect of the coupler instability load on the collision attitude of a train and the matching relationship between the coupler instability load and structural strength of the car body.

2.2 Three-stage rigid-flexible coupling finite element model of the coupler

To better simulate the collapse behavior of the coupler during a train collision and study the influence of the coupler buckling load on the collision buckling behavior of the train, a four-stage RFCFEM is proposed in this paper.The model is established based on a three-stage RFCFEM.We first introduce a three-stage RFCFEM and then describe the four-stage RFCFEM of the coupler.

Figure 2 shows the three-stage RFCFEM of the coupler.Compared with the RFEM, the three-stage RFCFEM simplifies the physical model of the coupler.It can simulate the energy-absorption characteristics of the buffer and collapse tubes.Moreover, the model can simulate the rotational characteristics of the rotary mechanism.However, it cannot simulate the elastic-plastic buckling characteristics of the coupler.

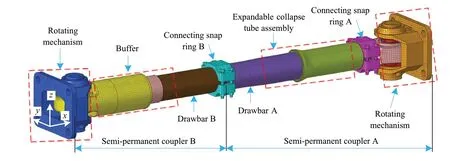
Fig.1 Refined finite element model (RFEM) of the coupler [27]

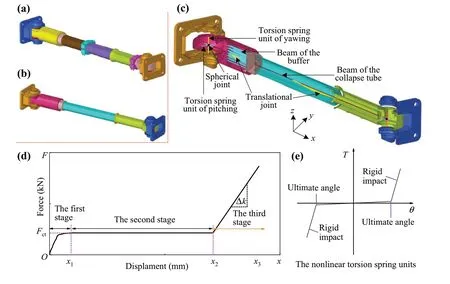
Fig.2 Three-stage rigid-flexible coupling finite element model (RFCFEM) of the coupler: a RFEM; b RFCFEM; c detailed model of RFCFEM;d input curve for the three-stage RFCFEM; e limit curve for coupler rotation angle

The beam element and #mat119 material were used to simulate the energy-absorption characteristics of the coupler buffer and collapse tube.Figure 2d presents the crush curve of the buffer and collapse tube.The deflection motion characteristics in thex-yandx-zplanes were realized using the rotating joint and spring units, and the deflection angle was limited, as shown in Fig.2e [12, 19].Thex-axis represents the train running direction, they-axis is perpendicular to thex-axis in the horizontal plane, and thez-axis is the vertical direction.

In previously established RFCFEMs of couplers,according to the load change during the longitudinal compression of the coupler, there are three stages: the buffer compression stage, the expandable collapse tube compression stage, and the rigid loading stage, as shown in Fig.2c.The first-stage buffer and second-stage collapse tube capacities (including the stroke and crushing force) are generally designed according to crashworthiness requirements.

2.3 Four-stage rigid-flexible coupling finite element model of the coupler

In the previous RFCFEM of the coupler, the third stage only provided stiffnessk.At this stage, the coupler force increased sharply as the collision progressed, resulting in a large plastic deformation of the vehicle body structure.During a collision, the coupler buckles when the load acting on it exceeds the buckling load, as shown in Fig.3a.

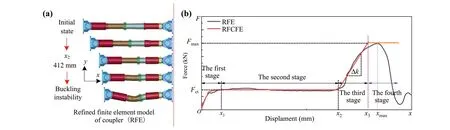
Fig.3 Input characteristic curve of four-stage rigid-flexible coupling finite element model (RFCFEM): a longitudinal compression deformation process of RFEM; b input curves for the four-stage RFCFEM

The deformation process and force-displacement curve of the refined coupler finite element model during longitudinal loading (along thex-direction) are shown in Fig.3.When the longitudinal compression displacement of the coupler exceeds the allowable maximum compression stroke, the drawbar of the coupler gradually experiences local plastic deformation until it reaches the overall buckling instability.The maximum load isFmax= 4994 kN; i.e.,the design instability load of the coupler is 4994 kN.This is not the theoretical value of the design, and 4994 kN is the longitudinal compression maximum load of the coupler without vertical and lateral deflections.The steadystate compression force of the expandable collapse tube isFct= 1500 kN.

According to the longitudinal compression process of the elastic-plastic coupler, a four-stage rigid-flexible coupling simulation method for the coupler is proposed in this study, as shown in Fig.3b.This method refers tox2-x3in the figure as the third stage, i.e., between the maximum effective compression stroke and the displacement when the maximum buckling load is reached.The fourth stage occurs after the maximum load is reached and corresponds to the horizontal line.The loading stage primarily affects the train crash response.Therefore, this study primarily considers the modeling of the coupler loading stage, and the unloading stage adopts a unified unloading stiffness curve.

The calculation methods for the stiffnesskof the third stage and the maximum loadFmaxof the fourth stage in the curve are as follows:

A linear function is used to fit the third-stage curve to the actual curve.The straight-line slope is the coupler stiffnessk, and the maximum coupler buckling load isFmax.This method requires obtaining the longitudinal compression force-displacement curve of the elastic-plastic coupler, as shown in Fig.3b, wherex2denotes the maximum allowable compression stroke of the coupler,Fmaxdenotes the coupler buckling load, andFctdenotes the steady-state crushing force of the collapse tube.

Figure 4a shows the force-time curve during longitudinal quasi-static loading at the coupler mount seat of the intermediate vehicle.Point 1 corresponds to the moment at which the underframe floor of the car body begins to deform plastically.Point 2 corresponds to the moment at which the vehicle body can bear the maximum load.Fpoint1is the force at which the car body structure begins to undergo obvious plastic deformation.

According to the force-time curve of the car body structure, when the force in the fourth stage is greater than the force of plastic deformation of the car body structure, there is a risk of plastic deformation of the car body structure.Compared with the actual coupler, the effects of the threeand four-stage rigid-flexible coupled models on the traincrash attitude response are different, and this is discussed in detail as follows.

Compared to the refined finite element model, the advantages of the four-stage RFCFEM are mainly in two aspects.

(1) In terms of modeling, the RFEM requires the creation of an elastoplastic structure containing the traction bar,expandable collapse tube assembly, and the rubber of the rubber bearing.In addition, solid units must also be used.Contact between the components must be considered.The modeling process is complex.The four-stage RFCFEM simulates the kinematic relationship between structures using hinges and the energy absorption of the coupler using beam units.The modeling is relatively simple.

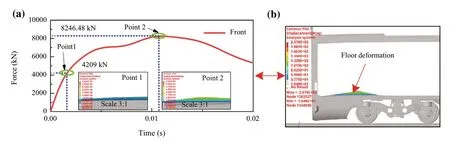
Fig.4 Intermediate vehicle distance and plastic deformation diagram: a force-time curve; b deformation of car body structure at 0.02 s

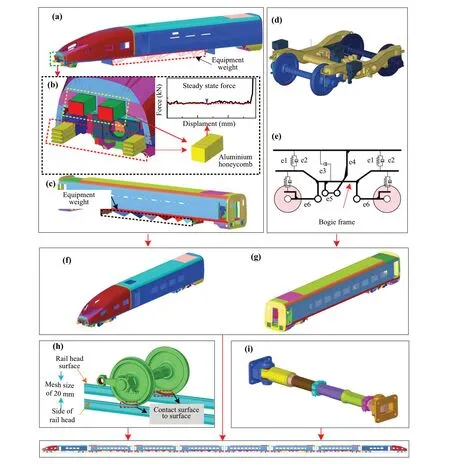
Fig.5 Collision simulation finite element model of eight marshaling trains: a head car body; b energy-absorbing and anti-climbing device; c middle car body; d FEM of the bogie; e suspension system simulation model of the bogie; f head vehicle; g middle vehicle; h wheel-rail contact model; i FEM of the coupler and draft gear (e1, air spring in the secondary suspension; e2, vertical damper of the secondary suspension; e3, lateral damper of the secondary suspension; e4, traction seat; e5, traction bar; e6, tumbler journal box; e7, journal box spring for the primary suspension;e8, vertical damper of the primary suspension; e9, elastic rubber joints and revolute joint for the wheelset)

(2) In terms of computational efficiency, as the refined finite element model uses elastic-plastic materials to simulate the plastic deformation of the coupler, smaller solid units must be used, and the computational time step must be reduced, which reduces the computational efficiency.

3 Train collision finite element model and collision scenario

According to the three-dimensional geometric model and parameters of an EMU train, a collision finite element model of eight marshaling trains is established using LSDYNA software, as shown in Fig.5.The proposed FE model mainly consists of four subsystems: (1) the head and middle vehicle model, (2) wheel-rail contact model,(3) energy absorption model including the coupler model and energy-absorbing anti-climbing device model, and (4)the rigid wall system.

The main structure of an EMU vehicle is made of an aluminum alloy, and the equipment adopts a mass unit.As shown in Fig.5a and c, the main structures, such as the wheelset, axle box, frame, and suspension system, are considered when establishing the finite element model of the bogie.The area where the wheelset contacts the rail is modeled using an elastic material and smaller-sized solid elements, whereas for the non-contact area, shell elements and a rigid material are used.The vertical, longitudinal, and lateral dynamic characteristics of the primary and secondary suspension systems are simulated using a 6-DOF nonlinear spring/damper element, as shown in Fig.5d, e, and h.A semi-permanent coupler is used in the train, as described in Sect.2.

The multistage energy-absorption system of a train includes a head coupler, energy absorption, anti-climbing,and intermediate coupler devices.The energy-absorbing device absorbs energy through the longitudinal compression deformation of the aluminum honeycomb.The total crushing force of the two energy-absorbing devices is 2100 kN,and the effective stroke is 385 mm.The two anti-climbing devices absorb energy through the inner-filled honeycomb aluminum with a total interfacial force of 900 kN.The effective stroke is 335 mm, as shown in Fig.5b.

This study uses an eight-marshaling train impacting a rigid wall with energy-absorbing and anti-climbing devices as an example, as shown in Fig.6.The collision speed is set at 25 km/h.Furthermore, the difference in the train collision response is analyzed to study the influence of different coupler models on the train collision response.

There are two train collision scenarios based on whether an impacted object can move.These include train-to-train and train-to-moving obstacles at level crossings, when the impacted object can move.The impacted object cannot move if the train impacts the surrounding buildings, station platform, or the buffer stop of the rail.When the train impacts a movable obstacle, a part of the collision kinetic energy of the train is converted into the kinetic energy of the movable object.The train and object run along the line at a certain speed.When a train impacts an immovable object, the collision kinetic energy of the train needs to be dissipated entirely, which causes a greater challenge for the energy dissipation system and occupant protection area.With the same collision kinetic energy, the collision between the train and immovable object is more dangerous.Therefore, this study considers a collision scenario between a train and an immovable rigid wall as an example.

The vehicle model and collision conditions are the same,but the coupler model differs.The third-stage stiffness andfourth-stage maximum load of the coupler are presented in Table 2.

Table 2 Stiffness and maximum load for different models

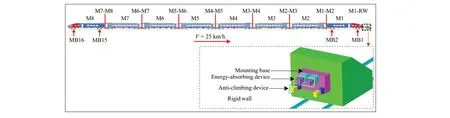
Fig.6 Train collision scenario.M1 to M8 are eight moving vehicles; MB1 and MB2 (M15 and M16) are the two bogies of M1 (M8); M1-RW denotes the collision interface between the train and rigid wall; Mi-Mj (i = 1,2,…,7; j = i + 1) denotes the collision interface between adjacent vehicles Mi and Mj.The front end of the vehicle is close to the collision interface, and the rear end is away.The energy-absorbing device and anti-climbing device installed on the rigid wall are the same as those installed on the train, and the vertical 40 mm offset is not set

(1) Train collision model 1: Refinement coupler finite element model.An elastic-plastic finite element model of the actual coupler is established, as shown in Fig.1.

(2) Train collision model 2: Three-stage rigid-flexible coupling finite element model of the coupler.The stiffness of the third stage is 41.614 kN/mm.

(3) Train collision model 3: Four-stage rigid-flexible coupling finite element model of the coupler.The stiffness of the third stage is 41.614 kN/mm, and the force of the fourth stage is the design buckling load (4994 kN) of the elastic-plastic coupler.

(4) Train collision model 4: Four-stage rigid-flexible coupling finite element model of the coupler.The stiffness of the third stage is 41.614 kN/mm, and the force of the fourth stage is the design buckling load of the elasticplastic coupler (4000 kN).

4 Analysis of train collision instability behavior

This section is primarily concerned with different analyses of vehicle attitudes under different collision models.Comparing the calculation results of the four models, the M2 car body exhibits the largest structural deformation and most severe wheelset derailment.Considering Model 2 with the largest deformation as an example, the vehicle attitude in the vertical and lateral directions is shown in Fig.7.

In the longitudinal direction, the plastic deformation at the end of M2 is larger than that at M3.The bogies of the two vehicles clearly derail in the vertical direction.In the lateral direction, vehicle buckling is mainly reflected in vehicles 1 to 4.The maximum lateral buckling displacement of M2 (993.61 mm) exceeds that of M3 (823.34 mm).In summary, with M2 as an example, it may be inferred that the lateral buckling displacement of a car body structure is the difference in lateral displacement between the coupler mounting bases at both ends of the vehicle.The main focus of this study is the process from train collision initiation to train derailment.Therefore, this study analyzes the train collision response in the time 0-0.6 s.

4.1 Longitudinal and vertical collision responses

According to the above description of the structural deformation of the car body and lateral buckling displacement,M2 is used as the analysis object, as shown in Fig.8.

Figure 8a shows the longitudinal and vertical deformations of M2 at 0.62 s.As evident from the figure, for the vertical deformation of the underframe floor relative to the underframe side beam: Model 2 (400 mm) > Model 3(84 mm) > Model 4 (50 mm) > Model 1 (40 mm).During the collision with Model 2, the excessive deformation of the front and rear ends of M2 results in a significant reduction in the occupant space.

Figure 8b shows the attitudes of the MB3 and MB4 bogies at 0.62 s and the wheelset lift curves.In the scenarios of Models 2 and 3, the lift of the wheelset is significantly larger than the allowable value of 21 mm in EN 15227 [28],and the wheelsets of both bogies are derailed.The maximum lift during the lifting process for each wheelset is listed in Table 3.Based on this analysis, compared with the calculation results of the three-stage rigid-flexible coupled finite element model, the collision response of the four-stage rigid-flexible coupled finite element model is closer to the collision response of the vehicle under the action of the refined finite element model.When the fourth-stage load in the four-stage finite element model of the coupler is considered as the critical load for the plastic deformation of the car body structure (Model 4), the train collision response attitude is basically the same as that of the refined coupler finite element model.The large buckling load of the coupler causes plastic deformation of the car body structure, reduces the space of the occupants, and leads to derailment of the wheelset.

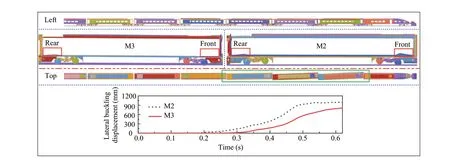
Fig.7 Train collision response attitude in Model 2 at time 0.62 s

Fig.8 Longitudinal and vertical deformation and buckling characteristics of the M2 vehicle: a longitudinal and vertical deformation of M2 at 0.62 s; b attitudes of the MB3 and MB4 bogies at 0.62 s and the wheelset lift curves.MB3-1 and MB3-2 (MB4-1 and MB4-2) denote the front and rear wheelset of the MB3 (MB4) bogie, respectively

4.2 Horizontal collision response

The lateral buckling behavior of a train collision is shown in Fig.9.As shown in Fig.9a, in the scenarios of Models 2 and 3, the train exhibits sawtooth buckling.In Models 1 and 4, the train exhibits no evident lateralbuckling behavior.Lateral buckling displacement of M2:Model 2, 993.61 mm > Model 3, 650.71 mm > Model 1,52.47 mm > Model 4, 50.74 mm.

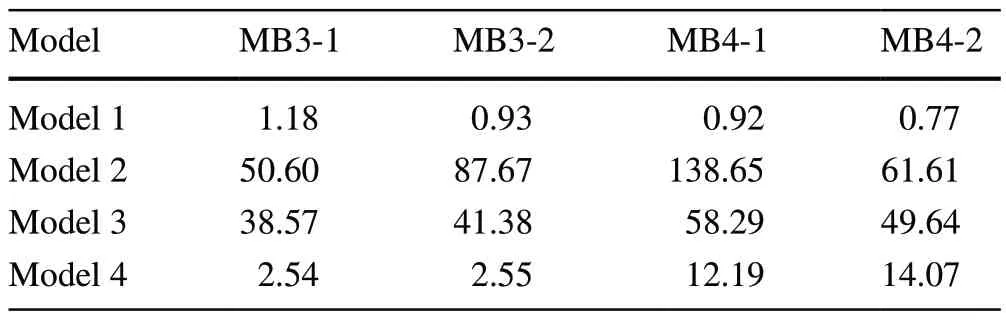
Table 3 Maximum wheelset lift for different models in lift stage(mm)

Table 4 Maximum lateral displacement of the wheelset for different models (mm)

Fig.9 Lateral buckling instability of train collision: a attitude of the train at 0.62 s and the lateral buckling displacement of M2; b lateral derailment attitude of the bogie at 0.62 s and the lateral displacement of the wheelset

Figure 9b shows the lateral attitude and wheelset lateral displacement curves of the MB3 and MB4 bogies at 0.62 s.In the Model 2 and Model 3 scenarios, the MB3 and MB4 bogies exhibit large-displacement lateral buckling.In the Model 1 and Model 4 scenarios, the MB3 and MB4 bogies continue to operate along the rails.The maximum lateral displacements of each wheelset are listed in Table 4.The maximum lateral displacement of the wheelset of Model 2, 544.48 mm > Model 3, 362.38 mm > Model 4,10.44 mm > Model 1, 8.62 mm.

Based on this analysis, when the fourth stage load is the critical load of plastic deformation of the car body structure (Model 4), Model 4 is consistent with Model 1 in terms of the train attitude, bogie attitude, and wheelset lateral displacement.During a train collision, the excessive buckling load of the coupler leads to sawtooth buckling of the train, large-displacement lateral buckling of the bogie, and derailment of the wheelset.

4.3 Mechanism of lateral buckling instability

According to the force-displacement curve in the longitudinal compression process of the refined finite element model of the coupler in Fig.3, the design buckling load of the coupler is 4994 kN.

According to Figs.8 and 9, the train in Model 1 does not appear to have lateral buckling instability during the collision.Nevertheless, the force of the fourth-stage coupler in Model 3 is 4994 kN.During the collision, the train exhibits lateral buckling instability, and the front-end deformation of the car body structure is twice that of Model 1.

As shown in Fig.10a, in the Model 1 scenario, the maximum longitudinal crushing force of the coupler during the train collision process is 3802 kN, and the buckling load at this time is the actual buckling load.Compared with the design buckling load of 4994 kN, the actual buckling load decreases by 23.87%.Figure 10b and c shows the angle change curve and buckling instability attitude of the M1-M2 coupler during collision, respectively.As the collision progresses, the pitch angle of the M1-M2 coupler gradually increases from 0° to 5°.At 0.174 s, when the coupler begins to buckle, the coupler pitch angle is 1.71° (allowable angle of 6°), and the lateral yaw angle is only 1.4° (allowable angle of 20°).

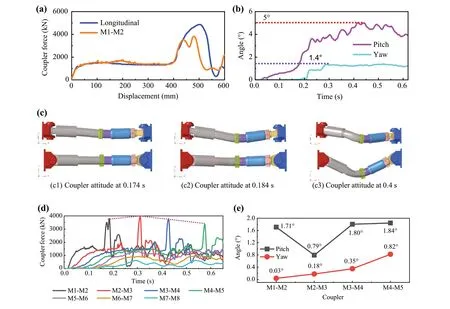
Fig.10 Buckling instability characteristics of the coupler in Model 1: a coupler longitudinal crushing force; b coupler pitch and yaw angle of M1-M2; c coupler attitude at M1-M2 interface; d coupler force-time curve of M1-M2 to M7-M8; e pitch and yaw angles for coupler buckling

Figure 10d shows the crushing force-time curve of the coupler in Model 1, and Fig.10e shows the pitch and yaw angles when the coupler starts to buckle.The coupler buckling load for M2-M3, 3947.814 kN > M1-M2, 3802.858 kN > M3-M4, 3791.128 kN > M4-M5, 3365.691 kN.The coupler pitch angle for M2-M3, 0.79° < M1-M2,1.71° < M3-M4, 1.80° < M4-M5, 1.84°.It can be observed that the changing trends of the actual buckling load of the coupler and pitch angle are opposite.For a smaller pitch angle, the actual buckling load of the coupler is greater.The vertical pitch angle reduces the buckling load of the coupler.Therefore, the coupler in Model 1 does not cause large deformations or lateral buckling instability in the car body structure.

The mechanism of lateral buckling instability during train collisions is complex.It is related to various factors, such as the vehicle type, relative state between vehicles, wheelrail state, and the matching degree of the coupler-car body structure.From the analysis of the results of the four models,it can be observed that the large actual buckling load of the coupler is an important factor in train collision instability and is also affected by the symmetry of the car body end structure.According to the previous analysis, the trains in Models 2 and 3 suffer lateral buckling instability and derail during the collision response process, with the train in Model 2 being the most dangerous.Therefore, the detailed analysis shown below is based on the calculation results of Model 2, as shown in Fig.11.

According to Fig.11a, the lateral buckling instability of the train is a gradual process during the collision.M2 first exhibits buckling instability, followed by M3 and M4.The bogie experiences a large lateral displacement and derails.M5-M8 do not exhibit lateral buckling instability.Figure 11b shows the process of lateral buckling instability and bogie derailment of M2.The process is as follows.

During a train collision, when the coupler is compressed to the maximum compression stroke, it enters the third stage and generates a large coupler force.After 0.25 s, under the action of the coupler forces, large plastic deformation occurs on the weak side of the car body structure.In this case,the load acting on both sides of the body structure is uneven.Moreover, the coupler deflects to the side with greater deformation.Under the action of the coupler force, the body structure continues to deflect toward the deformed side.When the deflection displacement of the car body structure is greater than the clearance between the traction pin and lateral stopping block of the bogie, the traction pin contacts the lateral stopping block of the frame.Under the continuous action of coupler forces, the car body structure drives the bogie to deflect continuously, resulting in wheelset derailment and sawtooth buckling of the train.

It is found that the core content has the following two aspects in the train collision instability process:

(1) The coupler has an actual buckling load greater than the plastic deformation of the car body structure, which causes the car body structure to undergo large plastic deformation before coupler buckling.

(2) The stiffness and strength of the two sides of the car body structure are asymmetric, resulting in a large deformation on the side with weak stiffness and strength.The end of the car body begins to deflect under the action of the coupler force.

According to the above analysis, the asymmetry of stiff-ness and strength on both sides of the vehicle structure leads to deflection of the car body structure during the deformation process, which subsequently causes lateral buckling of the train.To further verify that the asymmetry of stiffness and strength on both sides of the car body structure leads to asymmetric deformation of the car body structure as well as the strength difference between the two sides, the vehicle loading conditions shown in Fig.12a are formulated.

The intermediate vehicle is parked stationary on rails.The coupler mounting is statically compressed until the underframe is deformed plastically.A force-measuring spring is installed between the coupler mounting base and loading block, and the loading force at both ends of the vehicle body during the loading process of the loading block is measured using a force-measuring spring.There is a certain difference between the front and rear ends of the car body underframe floor, as shown at timet= 0 in Fig.12c.There is a noticeable hole on the right side of the rear underframe floor compared to the front underframe floor.

The force-displacement curve and chassis deformation during loading are shown in Fig.12b and c, respectively.The maximum loading force of the rear end is 7643.15 kN,the maximum loading force of the front end is 8246.48 kN,and the maximum load of the rear end increases by 7.89%.Under the same boundary conditions, floor holes reduce the bearing capacity of the underframe.During the deformation process, the rear-end underframe is deflected to the right side with the hole.The deformation of the front-end underframe is symmetrical.Therefore, the asymmetry of the underframe floor of the car body results in different bearing capacities on the left and right sides.The side with the weaker bearing capacity is deformed first, which in turn causes the entire underframe to deform and deflect toward the weaker side.Under the continuous action of the coupler force, the vehicle is deflected, which in turn causes the lateral buckling of the train.

Fig.11 Instability mechanism of train lateral buckling in Model 2: a lateral buckling instability process of train; b M1-M2 interface; c MB3 bogie; d MB3 attitude at 0.60 s; e lateral buckling data of M2

5 Conclusions

Based on previous research and the longitudinal crush characteristics of the coupler, a four-stage rigid-flexible coupling finite element model of the coupler is established.The influence of the fourth-stage coupler buckling load and asymmetry of the car body strength on the train collision buckling behavior is studied, and the following conclusions are drawn:

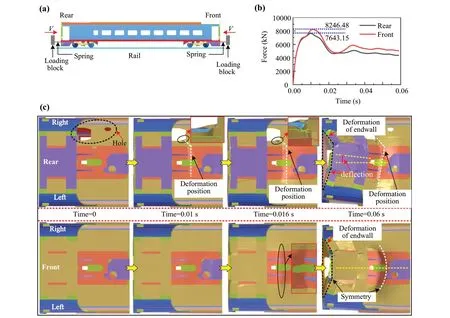
Fig.12 Loading deformation process at both ends of the car body structure: a loading condition; b loading force at coupler mounting base; c deformation process at both ends

(1) A four-stage rigid-flexible coupling finite element model of the coupler is established by combining the longitudinal crush characteristics of the refined finite element model verified by tests.A method for calculating the third-stage stiffness using the fitting method is proposed.

(2) The actual buckling load of the coupler and the asymmetry of the stiffness and strength of the car body structure in the lateral direction are important factors that cause lateral buckling during a train collision.If the stiffness and strength of the two sides of the car body structure are asymmetrical, the deformation of the weaker side is larger.The end of the car body begins to deflect under the action of the coupler forces.Sawtooth buckling of the train, large-displacement lateral buckling of the bogie, and derailment of the wheelset occur simultaneously.The asymmetry of the body structure results in a strength difference of 7.89% on both sides.The design should ensure that the stiffness strengths on both sides of the body structure are symmetrical.

(3) The design of an intermediate coupler should ensure that the actual buckling load is lower than the compressive load when the car body structure undergoes plastic deformation.The excessive buckling load of the coupler leads to the initiation of plastic deformation of the car body structure,thereby reducing the living space of the occupants.

In addition to the two factors of the actual instability load on the coupler and the lateral stiffness and strength asymmetry of the car body structure, train collision instability is influenced by a variety of factors.In future, it is also necessary to consider the influence of initial state differences between vehicles and wheel-rail state differences on train crash instability behavior to systematically summarize train collision instability behavior.

Acknowledgements This work was supported by the National Natural Science Foundation of China (No.52172409) and Sichuan Outstanding Youth Fund (No.2022JDJQ0025).

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence, and indicate if changes were made.The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material.If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.To view a copy of this licence, visit http:// creat iveco mmons.org/ licen ses/ by/4.0/.