针对标签噪声数据的自步半监督降维
古楠楠
(首都经济贸易大学 统计学院,北京 100070)
0 概述
在计算机视觉、医学数据处理、多媒体信息处理等领域通常面临很多高维数据,传统数据分析处理方法往往会遭遇维数灾难。降维是数据建模与数据挖掘的基本问题,根本任务是将样本从高维表示空间通过线性或非线性方法投影到低维本质特征空间,从而得到原高维数据的本质低维表示[1-3]。降维有利于节省数据的存储空间,在降低后续数据分析的时间代价的同时提升数据分析性能。从是否使用数据类别标签的角度可将降维方法分为无监督降维[4-6]、有监督降维[7-9]以及半监督降维[10-12]3 类。半监督降维同时利用少量有标签数据与大量无标签数据中蕴含的信息进行降维,在保持数据本质结构的同时提高所获低维表示的可分性与判别性。
基于图的半监督降维方法是一类重要且有效的半监督降维方法[10-12],已经获得了成功应用,但仍有一些尚未解决的问题,例如标签噪声问题。数据标记通常是一项乏味且主观的任务,费时费力,有时还需要专业知识背景,有些复杂数据还可能会因为具有较大的类内类间变化而增加标记难度,这些情况都会导致出现部分数据标记错误。事实上,标签噪声问题在实际应用中非常普遍,例如对于ImageNet等大规模图像数据集可能需要众包工人手工标注,由于知识受限或工作乏味,众包员工无法完全准确地注释特定任务,由此带来标签噪声[13]。当前已有一些针对噪声标签的研究[14],但在半监督降维领域,很少有专门针对具有标签噪声的数据进行处理的研究。当面对部分错误标记的训练数据时,半监督降维算法的性能可能会受到较大的影响,从而导致错误的模型预测或决策。
自步学习(Self-Paced Learning,SPL)[15]模仿人类由简单到复杂的学习方式,最开始利用简单样本训练模型以获取简单可靠的知识,然后反复地更新样本的简单度,以一种自步的方式逐渐将越来越多的从简单到复杂的样本纳入训练来学习更复杂与更专业的知识,实现对复杂事物的认知。自步学习能深层挖掘数据本质结构信息,对非凸优化问题可以避免局部最小值,提升算法性能,且对带噪声或奇异点的数据具有良好的鲁棒性[16]。
本文将自步学习机制融入用于降维的流形正则化框架[17-18],提出一个新的对标签噪声鲁棒的自步半监督降维(Self-Paced Semi-Supervised Dimensionality Reduction,SPSSDR)框架。在该框架下,设计SPSSDR 算法,基于交替优化策略,在更新降维映射函数和计算样本重要度两个步骤之间进行迭代。在计算降维映射函数时,基于流形正则化框架,考虑低维有标签数据的加权类内分散程度、降维映射的函数复杂度以及降维映射关于数据稀疏结构的光滑度。在计算样本重要度时,基于自步学习机制,计算有标签数据的低维表示与其所在类的锚点之间的距离,根据该距离进行样本重要度赋值。
1 相关工作
1.1 基于图的半监督降维
基于图的半监督降维方法通常先根据训练样本间的某种相似性度量建立一个或多个数据结构图,再在有标签数据的监督信息与结构图中隐藏的数据分布信息的协同指导下,获得数据的低维表示或高维空间到低维空间的特征映射。
SONG 等[19]提出半监督线性判别分析(Semi-Supervised Linear Discriminant Analysis,SSLDA)方法与半监督最大间距准则(Semi-Supervised Maximum Margin Criterion,SSMMC),它们在低维特征空间中最大化类间散度且最小化类内散度,同时保持数据结构图中隐藏的本质流形结构信息,以此获得降维映射函数。NIE 等[10]提出灵活的流形嵌入(Flexible Manifold Embedding,FME)方法,可以同时求出训练数据的预测标签、将数据映射到标签的线性回归函数以及两者之间的回归残差。NIE 等[11]提出基于图优化的半监督映射(Semisupervised Projection with Graph Optimization,SPGO)方法,该方法依据给定的高维数据的邻接矩阵、低维数据间的关系以及类别标签关于图拉普拉斯的光滑性,同时获得数据结构图与降维映射。WANG 等[12]针对半监督降维问题,提出一种基于结构图学习的标签传播(Label Propagation with Structured Graph Learning,LPSGL)方法,该方法同时执行标签传播、半监督结构图学习与降维,对有标签样本赋予不同的重要度来区分它们在降维映射学习中的不同影响。
1.2 自步学习
受人类和动物学习原理的启发,KUMAR 等[15]提出自步学习。自步学习引入自步参数(相当于人类的学习年龄)来控制学习的步调,从简单样本开始,不断增大自步参数(即增大学习年龄),使越来越多的从简单到复杂的样本被自动纳入模型进行训练,从而得到越来越成熟的模型。MENG 等[16]将SPL 问题归纳为如下的优化问题:
其 中:f:RD→R 是二分 类问题 的判别函数;L(zi,f(xi))为度量训练数据xi(i=1,2,∙∙∙,m)的真实标签zi和预测标签之间差异的损失函数;vi为反映训练数据xi重要度的权重;g(vi,λ)为决定学习机制的自步函数;λ是控制模型学习步调的自步参数。
目前,研究者们[20-22]已经提出了一系列自步学习方法,且已将自步学习成功应用于人脸[23]、临床疾病[24]、动作[25]等识别任务,自步学习机制对于实际应用中的复杂数据具有优越的处理能力,且对于有噪声或奇异点的数据具有良好的鲁棒性。
2 基于自步学习的针对标签噪声鲁棒的半监督降维
对于半监督降维问题,设训练数据集为{(xi,zi),xm+u,i=1,2,∙∙∙,m,u=1,2,∙∙∙,n-m},m为有标签数据的个数,n为样本总数,xi∊RD(i=1,2,∙∙∙,n)为高维训 练数据,D为高维 数据的维数,X=[x1,x2,∙∙∙,xm,∙∙∙,xn]∊RD×n为高维的训练数据矩阵,zi∊{1,2,…,C}为xi的类别标签,C为数据的类别总数。设d为低维空间的维数,yi∊Rd(i=1,2,…,n)为xi的低维表示,Y=[y1,y2,∙∙∙,ym,∙∙∙,yn]∊Rd×n为低维的数据矩阵。设高维空间到低维空间的降维映射函数为f=[f1,f2,…,fd]T:RD→Rd,则yi=f(xi)。向 量ai=[ai1,ai2,∙∙∙,ain]T∊Rn的L2 范数定义为为简便起见,将L2 范数用‖ ∙ ‖表示,向量ai∊Rn的L1 范数定义为向量ai∊Rn的L0 范数定义为ai的非零元素的个数。
2.1 针对标签噪声鲁棒的自步半监督降维框架
针对标签噪声鲁棒的自步半监督降维框架表示如下:
其中:优化变量f=[f1,f2,…,fd]T:RD→Rd为高维空间到低维空间的降维映射函数;优化变量v=[v1,v2,…,vm]∊Rm是反映有标签数据重要度的权重向量;γK和γI是两个正则化参数。
目标函数的第1 项为有标签数据的加权拟合损失项,度量了先验的指导信息yzi与通过降维映射所得的低维表示f(xi)之间的差异。L(∙,∙)是损失函数,如平方损失、Hinge 损失等。yj(j=1,2,…,C)为第j类数据的锚点,是利用某种方法预先得到并指派给第j类数据的先验低维表示指导信息。例如可以利用某种降维方法对数据进行预降维,计算每类低维数据的均值,将其作为该类的锚点。对于第j类有标签数据,使其低维表示集中在锚点yj附近。通过该方式,使降维后的同类数据尽可能靠近,异类数据尽可能分散,从而保留丰富的判别信息,使投影后的低维数据具有较大的可分性。
目标函数的第2 项为复杂度正则化项,度量了降维函数f在周围空间中的函数复杂度[17-18]。例如:若限制f属于某个再生核希尔伯特空间HK,则可以将‖f‖K定义为f在HK中的范数;若f是线性映射函数,即f(x)=WTx,则可以将‖f‖K定义为系数矩阵W的Frobenius 范数或L1 范数。
目标函数的第3 项为结构化信息正则化项,度量了降维函数f保持数据的结构化信息的能力。对训练数据构造结构化数据图,首先刻画数据间的结构化关系,例如可以构造刻画数据局部结构信息的K-近邻图,或者构造刻画数据全局结构信息的稀疏图[26]、低秩图[27]等,然后可以度量f在数据图上的光滑度,以此刻画f保持数据的结构化信息的能力。
目标函数的第4 项为自步学习正则化项,g(vi,λ)为决定学习机制的自步函数,λ是控制模型学习步调的自步参数。自步函数决定了模型学习新样本的模式,MENG 等[16]给出了自步函数的具体定义,研究者们也提出了不同的自步函数,如硬自步函数、软自步函数、混合自步函数等[15-16]。不同的学习场景与学习任务需要使用不同的自步学习机制,从而需要不同的自步函数。
在优化问题式(2)的约束项中的Ψi代表对有标签样本xi预先设定的课程,可以被视为一种先验知识。它是对有标签训练样本的权重的约束,模型在该约束下,反复调整有标签样本的权重,逐步从简单样本学习到复杂样本,得到一个成熟的模型。课程设计可以与先验、自步函数及特定任务相关,不同的样本也可以具有不同的课程。
2.2 针对标签噪声鲁棒的自步半监督降维算法
在所提的降维框架下,提出一种针对标签噪声鲁棒的自步半监督降维算法。
对于优化问题式(2)的目标函数的第1 项,即损失项,选用平方损失来度量数据的低维表示与其所在类的锚点之间的距离,如式(3)所示:
对于C类数据的锚点,利用局部保持投影(Locally Preserving Projections,LPP)[28]方法给 定。LPP 是一种经典的无监督线性降维方法,主要思想是将高维空间中邻近的点映射为低维空间中邻近的点。对于训练数据{x1,x2,…,xn},利用LPP 进行降维,得到低维表示然后对于每一类的锚点yj(j=1,2,…,C),将其设置为该类中的有标签数据的低维表示的均值,如式(4)所示:
其中:mj为属于第j类的有标签数据的个数。
对于优化问题式(2)的目标函数的第2 项,即复杂度正则化项,将‖f‖K定义为f在再生核希尔伯特空间HK中的范数。由于给定一个半正定的核函数K(∙,∙),会生成一个对应的再生核希尔伯特空间HK,因此假设fs∊HK(s=1,2,…,d),则函数f=[f1,f2,…,fd]T在HK中的范数的平方如式(5)所示,可以度量f在再生核希尔伯特空间中的复杂度。
对于优化问题式(2)的目标函数的第3 项,即结构化信息正则化项,利用f在结构化稀疏图上的光滑度来定义。数据xi的稀疏表示是指将xi用一个过完备字典中的一小部分元素的线性组合来表示。特别地,将训练数据作为字典,则xi的稀疏表示可通过如下的鲁棒L1 范数最小化问题来求解:
其 中:ai=[ai1,ai2,∙∙∙,ai,i-1,0,ai,i+1,∙∙∙,ain]T∊Rn为xi的稀疏表示系数向量;ei为考虑噪声或奇异点所设置的误差项。
然后构建结构化稀疏图[26],图的顶点集为训练数据集{x1,x2,∙∙∙,xm,∙∙∙,xn},由xj指向xi的边的权重为aij。已有理 论[29]证 明:xi的稀疏 表示系 数ai中 的非零元素自动对应xi同类的点,因此数据的稀疏图具有较强的判别性,有利于数据分类。为了使低维数据也具有同样的稀疏表示关系,可以将定义为f在稀疏图上的光滑度,以此来度量f保持数据稀疏表示结构的能力,如式(7)所示:
对于优化问题式(2)的目标函数的第4 项,即自步正则化项,将自步函数定义为硬自步函数[如式(8)所示],并将优化问题式(2)的约束项中的课程定义为Ψ[i如式(9)所示]。
在这样的设置下,所得的有标签数据的重要度为0 或1。当数据的类别标签错误时,自步学习机制会将数据的重要度赋值为0,这样就能消除错误类别标签造成的影响。当数据的类别标签正确时,自步学习机制会将数据的重要度赋值为1,此时能够充分利用数据类别标签中蕴含的判别信息,提升所得低维表示的判别性,有利于数据分类。
综上所述,在降维框架下,本文所提的针对标签噪声鲁棒的自步半监督降维算法可以表示如下:
对于自步半监督降维问题式(10),利用交替优化策略(Alternative Optimization Strategy,AOS)[15,30]进行求解。该方法将优化变量划分为k个互不相交的块,然后在迭代过程中交替优化每一个块中的变量。对于式(10),将变量分为两个互不相交的块:降维映射f与样本重要度v,并对它们进行交替求解。具体求解过程如下:
1)固定样本重要度v,优化降维映射f。此时式(10)转化为式(11):
定理1问题式(11)的最优解具有如下形式:
其中:bi=[b1i,b2i,∙∙∙,bdi]T∊Rd。
证明定理1 证明与文献[18]中定理2 的证明类似,因此不再详述。
设K=(K(xi,xj))∊Rn×n为核矩 阵,B=[b1,b2,…,bn]∊Rd×n为核函 数的系 数矩阵,A=[a1,a2,∙∙∙,an]T=(aij) ∊Rn×n为稀疏表示系数矩阵,tr(∙)为矩阵的迹,V∊Rn×n为第i(i=1,2,∙∙∙,m)个对角元素是vi、其余元素是0 的对角矩阵,I为n阶单位矩阵,YAnchor=为训练数据对应的类锚点矩阵。在式(12)的最优解表示形式下,问题式(11)可转化为关于矩阵B的优化问题:
令目标函数对B的偏导等于0,可得:
2)固定降维映射f,优化样本重要度v。此时式(10)转化为式(16):
该问题对于vi(i=1,2,∙∙∙,m)是可分离的,因此考虑如下的子优化问题:
推导得出该问题的最优解:
从式(18)可以看出,若有标签样本xi的低维表示与其对应类锚点之间的距离平方大于等于当前的年龄参数λ,意味着样本的类别标签可能是错误的或者样本是复杂难以学习的,则令其重要度。在下次迭代求降维映射f时:式(10)的目标函数的第1 项中的系数,意味着不考虑xi的类别标签zi;式(10)的目标函数的第3 项不受影响,意味着仍然考虑样本xi所刻画的数据结构信息。通过该方式,样本的错误标签会被过滤,只考虑正确的类别标签所提供的判别信息,同时无论具有正确标签还是错误标签的样本,都考虑其所刻画的数据稀疏结构信息。因此,所提算法对标签噪声具有较好的鲁棒性。
算法1针对标签噪声鲁棒的自步半监督降维算法
算法1 展示了本文所提的对标签噪声鲁棒的自步半监督降维算法。在该算法中,第1 和2 行是利用LPP 算法计算类锚点;第3 行是重要度的初始化;第4~8 行是利用交替优化策略求解自步半监督降维问题式(10),即对降维映射f与样本重要度v,每次固定一个,优化另一个。按照该优化策略,自步半监督降维问题式(10)的目标函数单调递减且具有下界,因此算法是收敛的。在算法最开始,自步参数λ被设定为一个很小的值,只考虑极少量的具有高可信度的样本类别标签。随着迭代次数的增加,λ逐渐增大,根据模型所学习到的信息,考虑越来越多具有判别性的可靠样本,而非可能具有误导性的模糊样本。通过该自步方式训练一个越来越成熟的模型,最终得到一个对噪声标签具有良好鲁棒性且具有较好判别性能的降维映射函数。
3 实验与结果分析
在公开的标准数据集上测试所提算法的性能,并与一些主流算法进行比较。实验采用的编程软件为MATLAB 2021b,操作系统为Windows 11,CPU为AMD Ryzen 7 5800H。
3.1 实验设置
在半监督降维常用的5 个数据集上进行实验:
1)YaleB 人脸数据集。该数据集中共有2 114 张图像,是38 个人分别在不同的光照条件下拍摄的脸部正面图像。每张图像都被处理为32×32 像素的灰度图并转换为1 024 维的向量。
2)CBCL 人脸数据集。使用的数据集中包含人脸图像和非人脸图像各1 000 张。每张图像都被处理为19×19 像素的灰度图并转换为361 维的向量。
3)ORL 人脸数据集。该数据集包含400 张人脸图像,是40 个人在不同的时间,通过改变光照方向、面部表情与面部细节拍摄的。每张图像都被处理为32×32 像素的灰度图并转换为1 024 维的向量。
4)USPS 手写数字数据集。该数据集包括了手写数字0 到9 的图像,每类有1 100 张分辨率为16×16 像素的图像并被转换为256 维的向量。在实验中,对于每个数字,随机选取了10%的图像进行实验。
5)CANE-9 文本数据集。该数据集来源于UCI数据集,包含属于9 个类别的共1 080 份文档,来源于一个名为“国家经济活动分类”表中的9 类巴西公司的自由文本业务描述。每个文档都被表示为一个856 维的向量,其分量表示关键词的权重,即该词在文档中出现的频率。
对比算法共计10 种,包括本文所提的自步半监督降维算法、Baseline、LPP[28]、线性判别分析(Linear Discriminant Analysis,LDA)、SSLDA[19]、SSMMC[19]、FME[10]、SPGO_KNN[11]、SPGO_sparse[11]、LPSGL[12],其中,Baseline 是指不进行降维而直接使用原始数据的算法,LPP 是无监督降维算法,LDA 是有监督降维算法,其他算法均为半监督降维算法。SPGO_KNN与SPGO_sparse 分别代表使用K-近邻图与稀疏图方法构造数据图,然后在此图上采用SPGO 进行半监督降维。与所提算法类似,LPSGL 也考虑了数据的重要度,但是从预先给定的候选集中选择样本的重要度。
对 于SSLDA、SSMMC、FME、SPGO_KNN 与SPGO_sparse 算法的 正则化参数,从{10-9,10-6,10-3,100,103,106,109}中进行选择。对于LPSGL算法,按照文献[12]所采取的策略,从{10-6,10-5,10-4,…,100,…,104,105,106} 中选择参数α与λ,从{100,101,102,103,104}中选择样本的重要度值v。对于所提算法,采取文献[18]所采取的策略,令并从{10-3,10-2,10-1,100}中选择CCK与CCI。对于基于K-近邻图的算法,按照文献[11-12]采取的策略,将邻域尺寸取为10,并利用高斯核来计算边的权重。
实验步骤具体如下:首先,利用PCA 对数据进行预处理,保持98%的数据信息;之后,随机选取占比为p的样本,赋予其错误的类别标签,即从其他C-1 个类中随机选择一个类别标签赋予该样本,利用五倍交叉验证来选择各算法的最优参数以及降维维数;随后,随机选择80%的数据作为训练数据,剩下的作为测试数据,在训练数据中随机选取30%的数据作为有标签数据,剩下的数据作为无标签数据,在训练数据上构造模型并利用所得的降维映射,获取无标签训练数据及测试数据的低维表示;最后,利用最近邻分类器来度量各算法的判别性能,即在低维空间中利用有标签训练数据构造分类器,再分别在无标签训练数据及测试数据上进行最近邻分类。
3.2 实验结果
对于每个实验数据集,将其随机进行20 次划分,得到不同的标签训练数据、无标签训练数据与测试数据,然后在每次划分上进行降维与分类。
3.2.1 分类结果
首先,计算各数据集在20 次随机划分上的平均分类准确率与标准差。所得结果如表1~表5 所示,其中,U 表示无标签训练数据上的分类结果,T 表示测试数据上的分类结果,每行的最优分类结果用粗体表示,次优结果用下划线表示(下同)。由表1~表5 可以看出,从平均分类准确率来看,所提算法具有最好的表现,尤其是对于有噪声标签的数据,在表1~表5 共计50 种情况中,只有在6 种情况下所提算法并非最优。

表1 YaleB 数据集上的分类准确率与标准差Table 1 Classification accuracy and standard deviation on the YaleB dataset %

表4 USPS 数据集上的分类准确率与标准差Table 4 Classification accuracy and standard deviation on the USPS dataset %

表5 CANE-9 数据集上的分类准确率与标准差Table 5 Classification accuracy and standard deviation on the CANE-9 dataset %
其次,计算各数据集在20 次随机划分上的平均Macro-F1 值,实验结果如表6~表10 所示。具体而言,分别计算无标签训练数据与测试数据中每个类别的分类准确率与召回率,由此得到每个类别的F1 值,然后计算所有类别的F1 值的算术平均值,即为Macro-F1 值。由表6~表10 可以看出,从Macro-F1 值来看,所提算法具有最好的表现,在表6~表10 共计50 种情况中,只有在4 种情况下所提算法并非最优,具体为CANE-9 训练与测试数据下噪声标签所占比率为0% 和10%,且在这4 种情况中,所提算法在3 种情况下为次优。

表6 YaleB 数据集上的Macro-F1 值Table 6 Macro-F1 values on the YaleB dataset

表7 CBCL 数据集上的Macro-F1 值Table 7 Macro-F1 values on the CBCL dataset
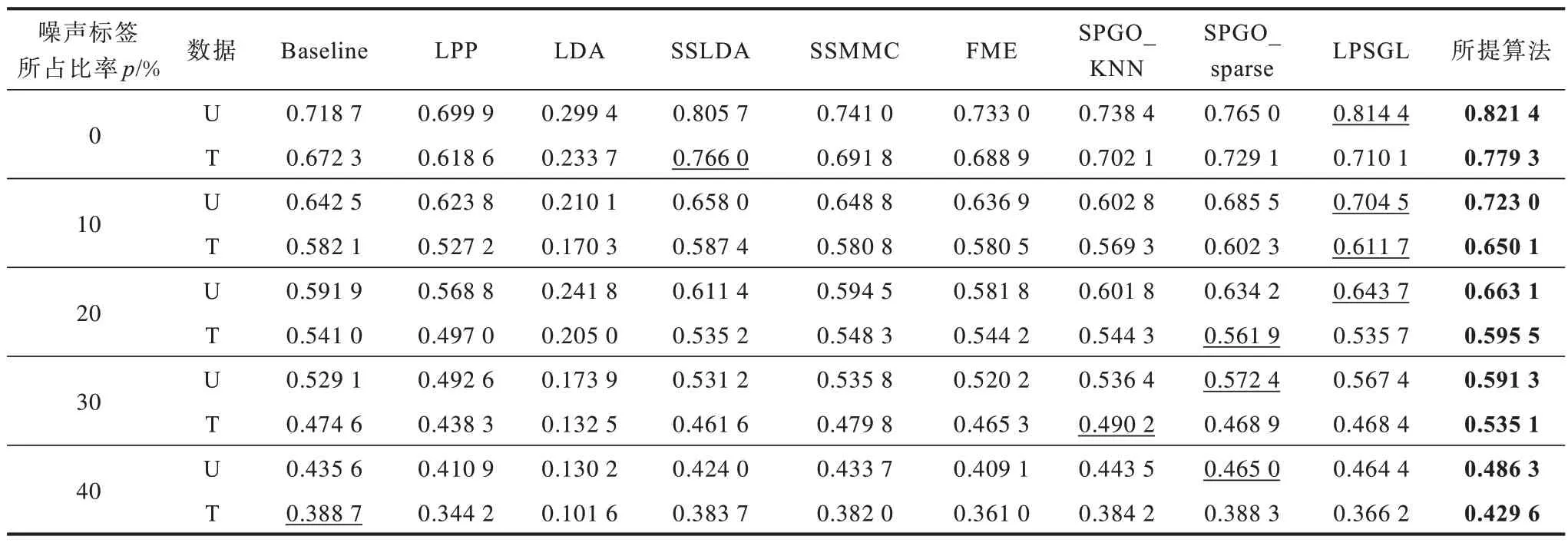
表8 ORL 数据集上的Macro-F1 值Table 8 Macro-F1 values on the ORL dataset

表9 USPS 数据集上的Macro-F1 值Table 9 Macro-F1 values on the USPS dataset
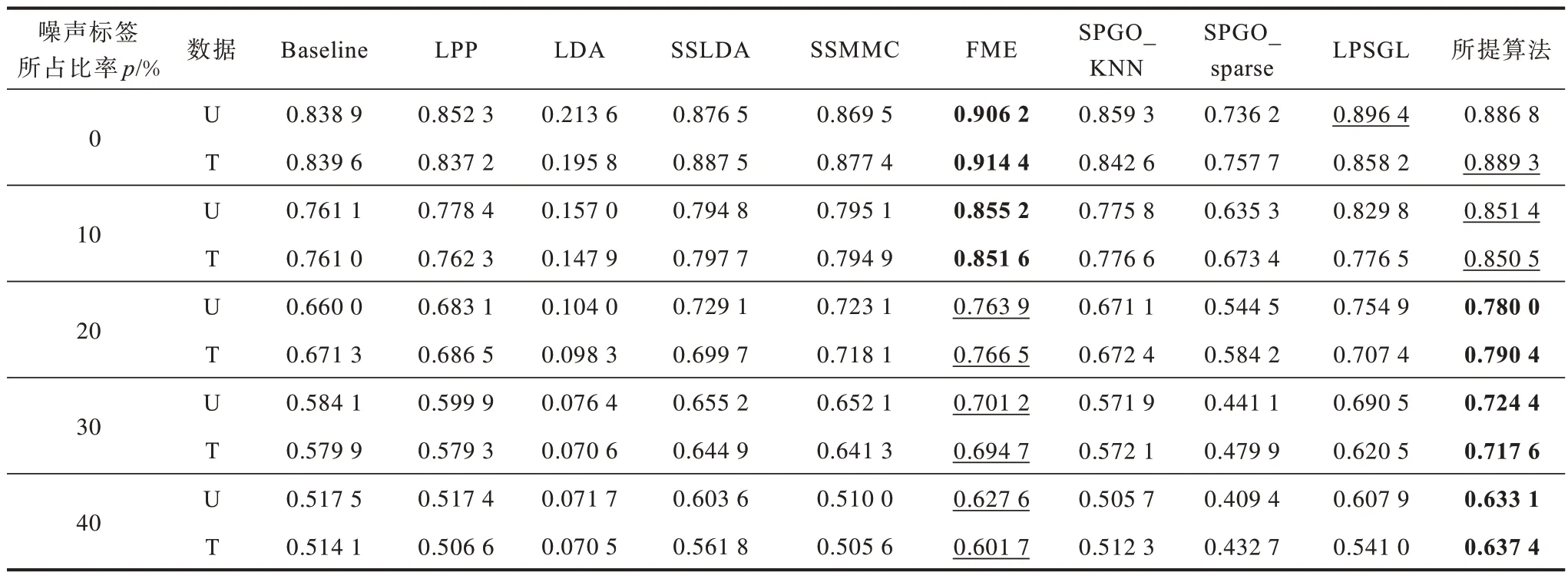
表10 CANE-9 数据集上的Macro-F1 值Table 10 Macro-F1 values on the CANE-9 dataset
从平均分类准确率与Macro-F1 值的结果可以看出,所提算法对标签噪声具有较好的鲁棒性。例如:对于CANE-9 数据集,当p较小时所提算法并非最优,随着p的增大,优势逐渐明显,成为最优算法;对于CBCL 数据集,在原始数据(p=0%)上所提算法比次优算法的分类准确率高0.4 个百分点(U)与0.5 个百分点(T),Macro-F1 值高0.004 5(U 和T);对于p=40%的噪声数据,所提算法比次优算法的分类准确率高2.8 个百分点(U)与3.2 个百分点(T),Macro-F1值高0.027 0(U)与0.031 6(T),与原始数据集相比提升幅度更大。
3.2.2 统计检验
在3.2.1 节中,从平均分类准确率与Macro-F1 值的角度验证了所提算法的有效性。为了进一步验证该有效性的统计显著性,将所提算法与其他算法的准确率进行成对T-检验。所得结果如表11~表15 所示,其中的数值表示该算法与所提算法的成对T-检验的P 值。由表11~表15 可以看出,在绝大多数情况下,T-检验的P 值小于0.01,说明从统计学意义来看,所提算法是具有显著优势的。

表11 YaleB 数据集上的T 检验的P 值Table 11 P-values of T-test on the YaleB dataset

表12 CBCL 数据集上的T 检验的P 值Table 12 P-values of T-test on the CBCL dataset
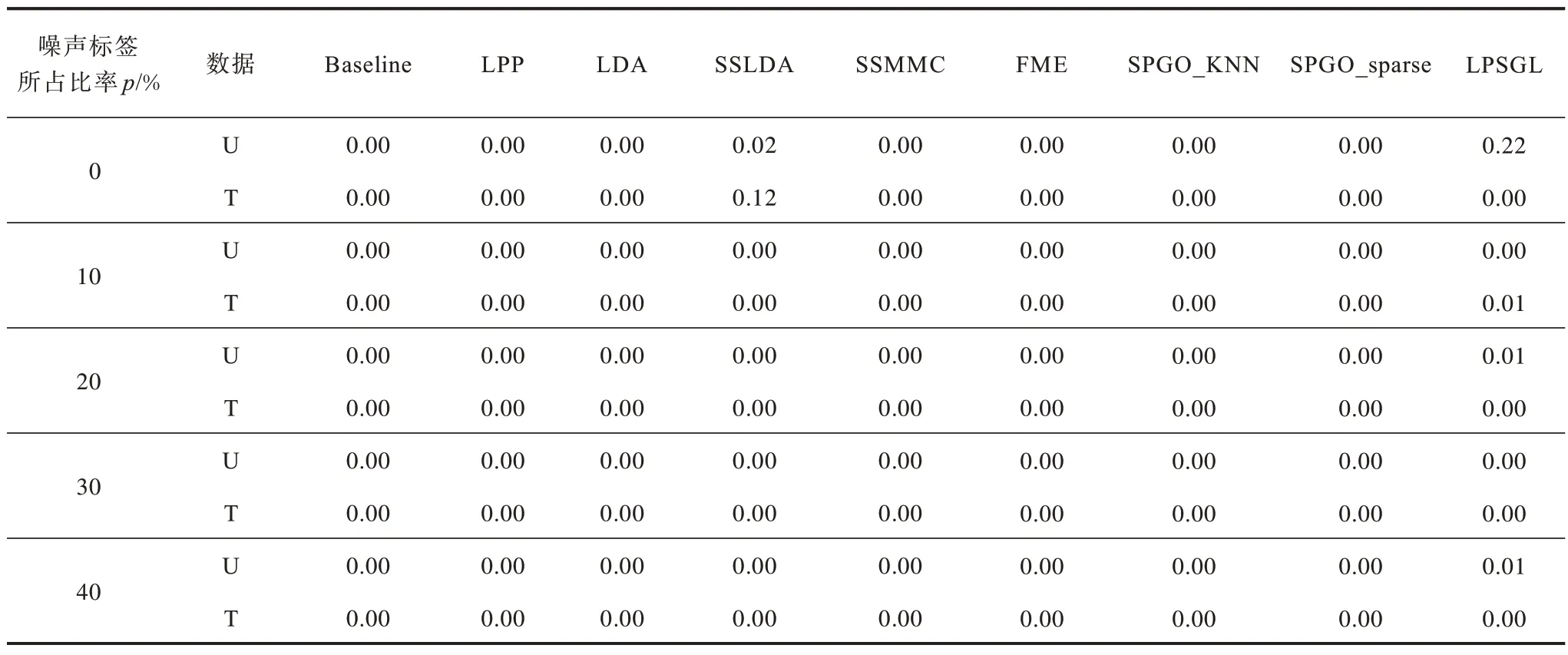
表13 ORL 数据集上的T 检验的P 值Table 13 P-values of T-test on the ORL dataset
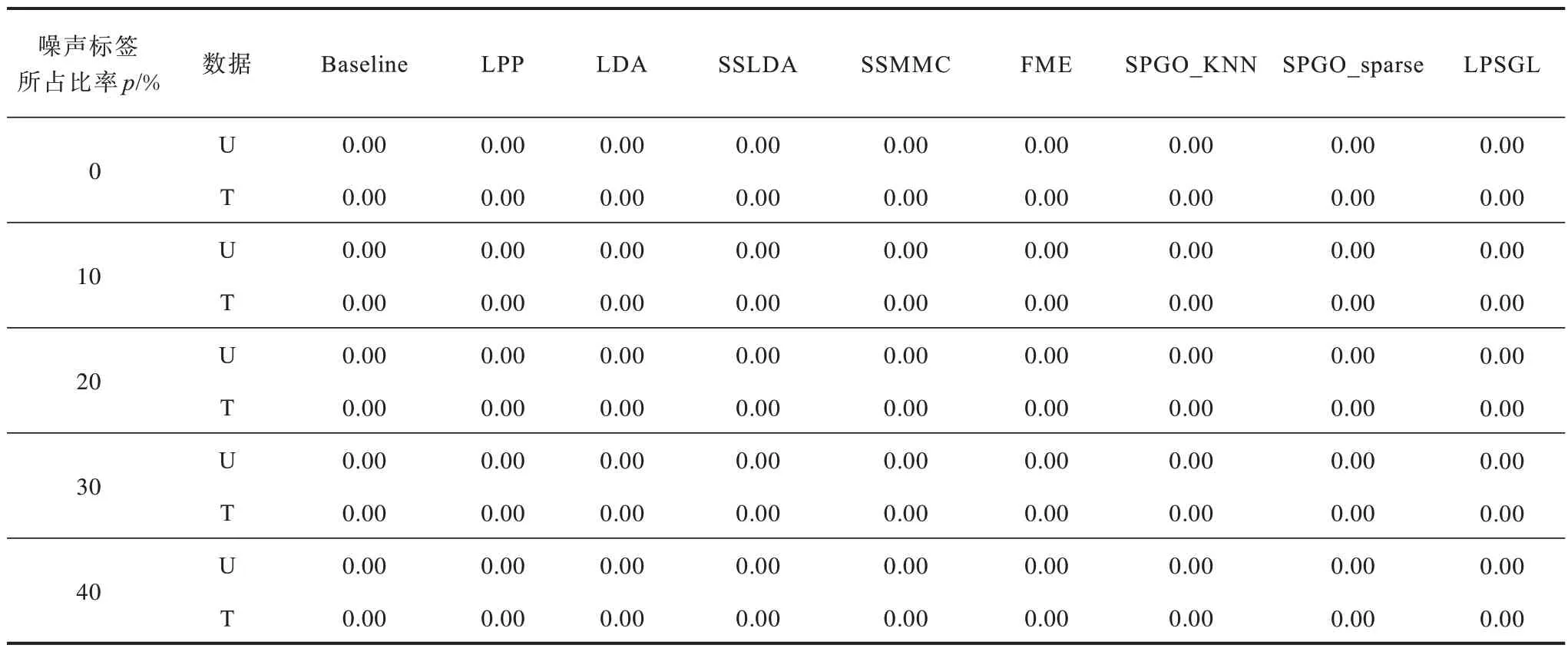
表14 USPS 数据集上的T 检验的P 值Table 14 P-values of T-test on the USPS dataset

表15 CANE-9 数据集上的T 检验的P 值Table 15 P-values of T-test on the CANE-9 dataset
3.2.3 参数敏感性分析
在本节中,对正则化参数CCK、CCI进行敏感性分析。以CBCL 与USPS 数据集为例,噪声标签所占比率p设置为20%,然后改变CCK、CCI的取值,分别计算20 次随机划分的无标签训练数据及测试数据上的平均分类准确率,实验结果如图1 所示。由图1 可以看出,当正则化参数CCK、CCI在较大范围内变化时,所提算法都具有较好的效果。

图1 在正则化参数的不同取值下所提算法的分类准确率Fig.1 Classification accuracy of the proposed algorithm under different values of regularization parameters
4 结束语
本文基于自步学习机制提出一个针对标签噪声鲁棒的自步半监督降维框架,并在此框架下设计自步半监督降维算法。该算法利用自步学习机制,自适应计算有标签样本的重要度且不断地进行更新,在此基础上逐步学习从简单到复杂的样本,因此对于噪声具有较好的鲁棒性,且可以获得具有非线性表达式的降维映射函数。然而,在所提算法中利用LPP 方法给定数据的类锚点,若类锚点设置错误则会影响后续的数据降维。另外,所提算法基于稀疏表示构建数据图,该数据图倾向于刻画数据的全局结构信息,而忽视了局部信息。下一步将构建更合理有效的数据类锚点以及能够更精确刻画数据结构信息且更具判别性的数据图。

