多个关键部件产品的破损边界
邓培畅,王志伟
多个关键部件产品的破损边界
邓培畅,王志伟*
(暨南大学 包装工程学院,广东 珠海 519070)
得到矩形冲击下具有多个关键部件产品的破损边界,并分析破损边界在线性和非线性(正切型和双曲正切型)情况下的变化规律以及影响因素。首先,使用集中质量法建立多自由度离散包装系统模型;然后,运用牛顿第二定律推导系统动力学方程,经无量纲处理后获得系统的无量纲动力学方程;最后,应用四阶龙格库塔法进行求解,获得系统的动力学响应,得到破损边界。相较于线性包装材料,双曲正切型缓冲包装材料可以扩大包装件的非破损区,而正切型缓冲包装材料则相反,且影响程度与非线性参数成正比;在特定情况下,不同关键部件的破损边界曲线存在相交情况。不同类型的冲击会导致不同关键部件的破损,实际物流过程中要考虑所有关键部件的保护。
冲击;破损边界;多自由度;非线性系统
在物流运输中,产品包装件经常因为振动冲击而破损,导致功能失效。因此,做好产品的包装防护十分重要,在进行产品的包装防护时,应该关注2个方面的内容:一是整个物流运输集装单元,二是其中的运输包装件。
在研究产品运输包装的动力学响应上,国内外学者已经取得了一定的成果。在对集装单元的研究方面,Urbanik[1]研究了多层堆码瓦楞纸箱包装在运输振动下的传递率曲线,Wolfenden等[2]、Marcondes等[3]、Jamialahmadi等[4]分别通过测力板、压力传感器、I-Scan系统测量了堆码包装的动压分布;Wang等[5-6]通过实验研究了多层堆码包装在随机振动下的动压分布和响应的统计特征;王志伟等[7]通过实验,得到了两层计算机堆码包装在随机振动下的动压分布和力水平穿越分布;王军等[8-9]建立了多层堆码包装系统动力学模型并求解,得到并讨论了脉冲幅值、材料阻尼及堆码层数对系统的冲击谱及破损边界的影响;林深伟等[10]通过实验和有限元分析研究了不同约束条件下两层堆码包装单元的随机振动响应功率谱;王志伟等[11]研究了不同约束条件下托盘堆码包装单元的随机振动响应;王志伟等[12]通过实验和有限元分析,得到了托盘运输包装单元的冲击响应。
在对单个产品包装件的研究方面,Newton等[13]在1968年提出的包装破损边界理论在评估包装防护性能方面得到了广泛的应用。Wang等[14-15]在此基础上提出了线性、非线性包装系统的跌落破损边界曲线的概念,并推广至具有关键部件的两自由度包装系统。随后,人们的对破损边界的研究开始从二维的曲线转向三维的曲面。王军等[16]以正切型包装为例,提出了考虑易损件的产品包装冲击破损边界曲面概念;王军等[17]研究了两自由度双曲正切型包装关键件的三维冲击谱特性;姜权等[18]提出了两自由度三次非线性包装系统关键部件在运输过程中的破损边界曲面评价方法;严敏等[19]构建了斜支承系统的三维跌落破损边界曲面;杜兴丹等[20]使用牛顿谐波法求解跌落冲击条件下悬挂包装系统的加速度响应近似解析解,并与四阶龙格-库塔数值解及VIM近似解相比较,验证了结果的正确性并进一步研究了该系统的破损边界曲线;李志强等[21]通过实验获得了半正弦冲击下烤箱的脆值以及破损边界曲线,为缓冲包装设计的合理性提供依据;段宁宁等[22]建立了考虑关键件的斜支承包装系统模型,使用四阶龙格-库塔法获得了系统关键件的跌落破损边界,并分析了支承角、频率比、系统阻尼比对破损边界的影响。
可以看出,学者们对包装破损边界的研究大都局限在单自由度或两自由度,但实际包装产品大多数具有多个复杂结构,产品的破坏可能出现在任何一个关键部件之中,不考虑或仅考虑一个关键部件不足以体现实际运输产品,导致结果与实际情况发生偏差。因此,建立具有多个关键部件包装系统的跌落评估方法十分有必要。本文将具有多个关键部件的包装系统建立为+1自由度系统,通过数值模拟的方法,探索多自由度线性和非线性包装系统的冲击破损边界曲线和曲面,并根据模拟过程中出现的现象得出了一些结论。
1 系统模型及方程
本文采用集中质量法[23]建立了一般化的离散包装系统模型。假设整个包装系统由一个主体部件和一系列关键部件组成,每个部件都可以看成为是一个质量块,各关键部件与产品主体之间都为线弹性材料,不存在非线性特征。此时,整个包装系统可以用一个具有+1自由度的质量-弹簧-阻尼系统表示,如图1所示(为关键部件数量)。

图1 n+1自由度离散包装系统模型

该模型可以用微分方程组(1)描述。

引入相对位移:

并转化为无量纲方程组:

其中:

则产品部件p和关键部件m的加速度响应见式(5)。

对于线性系统,有:
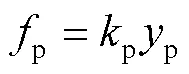
则:

对于正切型非线性系统,有:

则:

对于双曲正切型非线性系统,有:

则:
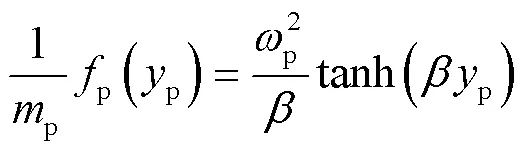


脉冲速度改变量为:

2 冲击模型破损边界的数值求解
2.1 线性包装系统

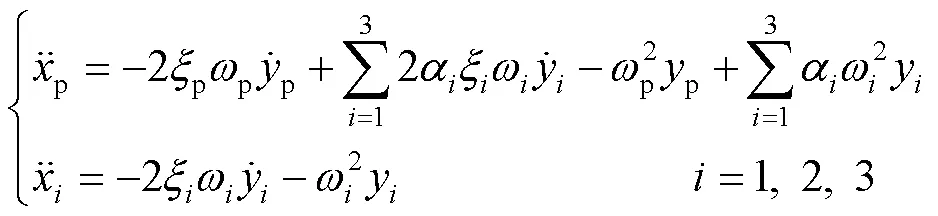
现假定系统各参数如下:
图2 线性包装系统破损边界曲面
Fig.2 Damage boundary surface of linear packaging system

2.2 正切型非线性包装系统

可以看出,与线性系统相比,其加速度响应还与非线性特征参数有关,假定=50,其他参数不变,得到各部件的破损边界曲面见图3。
从图3中可以看出,相较于线性包装缓冲材料,正切型非线性缓冲材料致使各部件的临界速度线和临界加速度线变小,导致破损区变大,各部件更加容易因为冲击而损坏。
2.3 双曲正切型非线性包装系统
将=3和式(11)代入式(5),可以得到3+1自由度双曲正切型非线性离散包装系统的主体部件p和关键部件m的加速度响应为:

3 若干数值结果分析
3.1 非线性-线性关系
通过对图2~4的对比分析可以看出,无论是产品主体还是各关键部件,相较于线性系统,正切型和双曲正切型非线性系统各部件的破损边界曲面发生显著变化,并且同一个非线性参数下,不同部件破损边界曲面所体现的非线性特征强度是不一样的。


图3 正切型非线性包装系统破损边界曲面

图4 双曲正切型非线性包装系统破损边界曲面

图5 不同非线性参数(β)下正切型非线性包装系统破损边界曲线
从图5、图6可以看出,随着非线性参数的增大,各部件的破损边界曲线相较于线性系统所产生非线性的偏移程度不断增大,非线性特征也更加明显,但偏移速率不断减小,且主体部件相较于关键部件,偏移程度更大,特征更明显。
3.2 3个系统特殊参数下的现象
3.2.1 线性系统
假定系统各参数如下,求解各关键部件的破损边界曲线如图7所示。

图6 不同非线性参数下双曲正切型非线性包装系统破损边界曲线

图7 特殊情况下线性系统各关键部件破损边界曲线
3.2.2 正切非线性系统
假设系统的各参数值如下所示,画出各关键部件的破损边界曲线如图8所示。

图8 特殊情况下正切型非线性系统各关键部件破边界曲线
p=2π×20,1=2π×40,2=2π×6,3=2π×60
=120
3.2.3 双曲正切非线性系统
假设系统的各个参数设定为以下数值,得到各关键部件的破损边界曲线如图9所示。
p=2π×20,1=2π×40,2=2π×6,3=2π×60
=120

图9 特殊情况下双曲正切型非线性系统各关键部件破损边界曲线
根据上述结果可以看出,在线性和非线性包装系统中,都存在特定参数,使得3个关键部件的破损边界曲线相交。这说明在不同类型的冲击作用下,产品的易损件是不同的,不同的冲击载荷会导致不同关键部件先一步发生损害,脆值小的关键部件在物流过程中不一定最先发生破坏。
4 结语
包装的破损边界是衡量包装防护性能的有效指标,本文使用数值模拟的方法求解了具有多个关键部件的线性和非线性包装系统的破损边界,得出以下结论:
1)一般来说,产品包装件在运输过程中受到冲击时,由于关键部件的脆值相对较低,比产品主体更容易受损。
2)相较于线性缓冲包装材料,双曲正切型非线性缓冲包装材料能有效地扩大产品的非破损区,而正切型非线性缓冲包装材料则相反,会扩大包装件的受损区。
3)关键部件的固有频率会对其本身的破损边界产生影响。当关键部件的固有频率和缓冲系统的固有频率相同时,关键部件会吸收更多的冲击能量,更加容易受损。
4)双曲正切型和正切型非线性包装系统的非线性特征参数越大,其非线性特征越明显,相较于线性系统偏移得越大。
5)不同冲击载荷会导致不同关键部件的损坏,某些情况下,大脆值的关键部件会比小脆值的关键部件先发生破损。说明在不同类型的冲击作用下,产品的易损件不同,只关注较低脆值关键部件是不够的,因此需要关注所有关键部件的保护。
[1] URBANIK T J. Transportation Vibration Effects on Unitized Corrugated Containers[M]. Madison: Department of Agriculture, Forest Service, Forest Products Laboratory, 1978.
[2] WOLFENDEN A, URBANIK T. Force Plate for Corrugated Container Vibration Tests[J]. Journal of Testing and Evaluation, 1990, 18(5): 359-362.
[3] MARCONDES J A, SCHUENEMAN H. Measurement and Analysis of Dynamic Forces within a Stack of Packages[C]// Proceedings of the 20th IAPI Symposium, San Jose, 2000.
[4] JAMIALAHMADI A, TROST T, OSTLUND S. A Proposed Tool to Determine Dynamic Load Distribution between Corrugated Boxes[J]. Packaging Technology and Science, 2011, 24(6): 317-330.
[5] WANG Z, FANG Ke. Dynamic Performance of Stacked Packaging Units[J]. Packaging Technology and Science, 2016, 29(10): 491-511.
[6] FANG K, WANG Z W. The Statistical Characteristics of Maxima of Contact Force in Stacked Packaging Units under Random Vibration[J]. Packaging Technology and Science, 2018, 31(5): 261-276.
[7] 王志伟, 戚德彬. 两层计算机堆码包装动力学试验研究[J]. 机械工程学报, 2017, 53(3): 90-99.
WANG Zhi-wei, QI De-bin. Experimental Study of Dynamic Response of Two Layers Stacked Packaging Units of Computers[J]. Journal of Mechanical Engineering, 2017, 53(3): 90-99.
[8] 王军, 王志伟. 多层堆码包装系统冲击动力学特性研究(Ⅰ): 冲击谱[J]. 振动与冲击, 2008, 27(8): 106-107.
WANG Jun, WANG Zhi-wei. Combined Shock Spectrum of Linear Stacking Packaging System[J]. Journal of Vibration and Shock, 2008, 27(8): 106-107.
[9] 王军, 王志伟. 多层堆码包装系统冲击动力学特性研究(Ⅱ): 破损边界[J]. 振动与冲击, 2008, 27(8): 108-109.
WANG Jun, WANG Zhi-wei. Combined Damage Boundary Curve of Linear Stacking Packaging System[J]. Journal of Vibration and Shock, 2008, 27(8): 108-109.
[10] 林深伟, 王志伟. 两层堆码包装单元的随机振动响应[J]. 包装学报, 2017, 9(4): 10-19.
LIN Shen-wei, WANG Zhi-wei. Response of Two Layer Stacked Packaging Unit in Random Vibration[J]. Packaging Journal, 2017, 9(4): 10-19.
[11] 王志伟, 曹燕. 托盘堆码包装单元随机振动响应的实验研究[J]. 振动工程学报, 2021, 34(6): 1187-1197.
WANG Zhi-wei, CAO Yan. Experimental Investigation on Response of Random Vibration for Pallet Stacked Packaging Unit[J]. Journal of Vibration Engineering, 2021, 34(6): 1187-1197.
[12] 王志伟, 伍炼. 托盘运输包装单元冲击响应的试验与有限元分析[J]. 振动与冲击, 2021, 40(16): 124-131.
WANG Zhi-wei, WU Lian. Experimental Study and Finite Element Analysis of Impact Response of Pallet Stacked Transportation Packaging Units[J]. Journal of Vibration and Shock, 2021, 40(16): 124-131.
[13] NEWTON R E. Fragility Assessment Theory and Test Procedure[M]. Monterey, CA: Monterey Research Laboratory, 1968.
[14] WANG Zhi-wei. On Evaluation of Product Dropping Damage[J]. Packaging Technology and Science, 2002, 15(3): 115-120.
[15] WANG Zhi-wei. Dropping Damage Boundary Curves for Cubic and Tangent Package Cushioning Systems[J]. Packaging Technology and Science, 2002, 15(5): 263-266.
[16] 王军, 王志伟. 考虑易损件的正切型包装系统冲击破损边界曲面研究[J]. 振动与冲击, 2008, 27(2): 166-167.
WANG Jun, WANG Zhi-wei. Damage Boundary Surface of a Tangent Nonlinear Packaging System with Critical Component[J]. Journal of Vibration and Shock, 2008, 27(2): 166-167.
[17] 王军, 卢立新, 王志伟. 双曲正切包装系统关键部件三维冲击谱研究[J]. 振动与冲击, 2010, 29(10): 99-101.
WANG Jun, LU Li-xin, WANG Zhi-wei. Three-Dimensional Shock Spectrum of a Hyperbolic Tangent Nonlinear Packaging System with Critical Component[J]. Journal of Vibration and Shock, 2010, 29(10): 99-101.
[18] 姜权, 王军, 卢立新, 等. 三次非线性包装系统关键部件破损曲面研究[J]. 包装工程, 2012, 33(17): 53-56.
JIANG Quan, WANG Jun, LU Li-xin, et al. Damage Boundary Surface of Critical Components of Cubic Nonlinear Packaging System[J]. Packaging Engineering, 2012, 33(17): 53-56.
[19] 严敏, 陈安军. 斜支承系统包装物体的跌落破损边界研究[J]. 噪声与振动控制, 2014, 34(1): 88-91.
YAN Min, CHEN An-jun. Study on Dropping Damage Boundary of Tilted Support Package System[J]. Noise and Vibration Control, 2014, 34(1): 88-91.
[20] 杜兴丹, 陈安军. 基于牛顿谐波平衡法悬挂系统跌落冲击动力学性能评价[J]. 振动工程学报, 2020, 33(2): 331-337.
DU Xing-dan, CHEN An-jun. Dropping Shock Dynamic Performance Evaluation of Suspension System Based on NHB Method[J]. Journal of Vibration Engineering, 2020, 33(2): 331-337.
[21] 李志强, 王羽星, 张素风. 半正弦激励下烤箱脆值及破损边界曲线试验分析[J]. 包装工程, 2020, 41(5): 165-171.
LI Zhi-qiang, WANG Yu-xing, ZHANG Su-feng. Experimental Analysis of Fragility and Damage Boundary Curve of Oven under Half-Sinusoidal Excitation[J]. Packaging Engineering, 2020, 41(5): 165-171.
[22] 段宁宁, 余立. 斜支承系统关键件的跌落破损评价[J]. 噪声与振动控制, 2019, 39(1): 186-191.
DUAN Ning-ning, YU Li. Dropping Damage Evaluation for Critical Components of Tilted Support Systems[J]. Noise and Vibration Control, 2019, 39(1): 186-191.
[23] WANG Zhi-wei, WANG Li-jun. Accelerated Random Vibration Testing of Transport Packaging System Based on Acceleration PSD: Accelerated Random Vibration Testing of Transport Packaging[J]. Packaging Technology and Science, 2017, 30(7): 621-643.
Damage Boundary for Products with Multiple Critical Components
DENG Pei-chang, WANG Zhi-wei*
(College of Packaging Engineering, Jinan University, Guangdong Zhuhai 519070, China)
The work aims to obtain the damage boundary of product with multiple critical components under rectangular impact, and analyze the change rules and influencing factors of the damage boundary under linear and nonlinear (tangent and hyperbolic tangent) conditions. First, the lumped mass method was adopted to establish a MDOF discrete packaging product system model. Second, the kinematic equations of the system were derived according to the Newton's second law, and dimensionless dynamic equations of the system were obtained through dimensionless processing. Third, the dynamic response of the system was solved according to the fourth-order Runge-Kutta method, and the damage boundary wasobtained. The results showed that compared with linear packaging materials, hyperbolic tangential buffer packaging materials could expand the non-damaged zone of the package, while tangential buffer packaging materials could expand the non-damaged zone, and the influence degree was proportional to the nonlinear parameters. In some cases, the damage boundary curves of different critical components were intersected. In conclusion, different types of impact will lead to the damage of different critical components, and the protection of all critical components should be considered in the actual logistics process.
impact; damage boundary; multiple degrees of freedom; nonlinear system
TB485.3;TH485.1
A
1001-3563(2023)21-0046-08
10.19554/j.cnki.1001-3563.2023.21.006
2023-06-09
国家自然科学基金(50775100)
通信作者
责任编辑:曾钰婵

