基于全球预报系统气温的降尺度研究
张茂林,邓小波,刘海磊,刘梦琪,陈卫星
(成都信息工程大学电子工程学院,四川成都 610225)
0 引言
气温(Ta)是区域和全球尺度辐射平衡、能量收支和水循环研究的关键参数。气温数据也是陆面过程建模的重要输入[1],如地表蒸散发估算[2]、农田监测[3]和气候变化分析[4]。获取气温的传统方法是在地面站进行测量。然而,测得的气温点不能反映大面积的温度[5]。空间插值法可将离散空间分布的地面站所测量的气温扩展到大面积,其中一个常用的因素是距离[6]。除考虑气温变化和距离的空间相关性外,进一步发展了先进的插值方法,纳入更多的因素,如海拔、纬度和经度[7],但空间插值不适用于地面站不足的地区。
气候模型已被证明是调查气候系统和气候变化的有效工具,可获全球范围的气候数据。近年来,CMIP5(coupled model intercomparison project 5)利用全球气候模型(GCM)开发了大量气候模拟[8]。随着气候模式的发展,已经生成可提供长期气温的产品,如国家环境预测中心和国家大气研究中心(NCEP/NCAR)已经生成了可供用户使用的再分析数据集和ERA5 再分析数据集[9-11]。尽管这些GCM 可以捕捉到主要的大尺度环流特征,但其在区域气候模拟中的应用研究有限,因为它们的空间分辨率从0.0625°~1°甚至更粗,无法获得区域尺度上气候特征的有用信息[11-12],特别是在地形变化剧烈的山区[13]。
为满足局部地区的应用,如何获得中高空间分辨率的气温数据已成为关注的焦点,从全球气候模型(GCM)做出的大规模气候预测中提取局部或区域尺度信息的过程称为缩小尺度,也称之为降尺度。气候变化文献中存在动态降尺度和统计降尺度两大类降尺度方法。动态降尺度方法是建立在区域气候模式(regional climate model,RCM)基础上的,GCM 为RCM 提供初边值条件,通过高分辨率区域气候模式的数值积分获得高分辨率天气气候信息[14]。RCM 采用数学物理方程描述气候系统内部的各种动力和热力学过程。随着地球生物化学等过程的引入,区域气候模式正逐渐向区域地球系统模式方向发展,这些模式可以描述大气—陆地—水—经济等过程之间的相互作用[15-16]。然而,动力降尺度需要大量的计算资源,随着区域气候模式分辨率的提高,计算量呈指数形式增长。
统计降尺度方法建立在观测的局地气候与大尺度场之间的统计关系基础上,假定上述统计关系在未来的气候情景下仍然适用,从而实现对全球模式未来气候变化预估结果的降尺度。统计降尺度有以下优点:能够以很高的计算效率由大尺度气象要素得到区域尺度的气象要素;能输出较高分辨率或站点尺度的气象要素;模型参数可以受区域下垫面特征的控制。统计降尺度能够弥补动力降尺度的一些不足,因而得到广泛应用[17-19]。
统计降尺度已被证明是提高气温空间分辨率的有效工具。Schoof 等[20]检验了回归模型和神经网络模型在气温降尺度中的表现;通过这两种模型的简化,得到了相似的结果。通过选择中欧和西欧作为研究区域,Huth[21]开发了一种统计方法,通过站点网络对每日测量的气温进行降尺度处理,引导许多科学家开始关注通过降尺度获取中等空间分辨率的气温。Pan[13]利用天气研究与预报(weather research and forecasting,WRF)模型生成了一个5 km/1 h的气温数据集,用于驱动中国黑河流域的水文模型。Hofer 等[22]利用统计降尺度方法获得了数据稀疏冰川山脉环境下的气温。Jha[23]提出了气温降尺度的地质统计学框架。
Ramírez 等[24]分别针对不同的地域,将神经网络(NN)与线性回归、CCA 等线性方法用于统计降尺度的对比研究,表明多数情形下NN 的降尺度能力更好。因此,本研究构建一个神经网络降尺度模型(DS),用于建立台站观测气温与气候模式数据,包括GFS 气温数据、海拔(ElE)数据和归一化植被指数(NDVI)数据等之间的关系。然后将该网络模型用于高空间分辨率气温制图,并通过大量实验验证其有效性和优越性。
1 区域和数据
1.1 研究区域
研究区域为中国湖南省(108.8 °E~114.2 °E,24.7 °N~30.1 °N)。作为中国的内陆省份,湖南拥有复杂的地理环境,海拔高度0~2100 m,拥有多种地貌特征,山地占全省总面积的51.22%,丘陵占15.40%,岗地占13.87%,平原占13.11%,水面占6.39%。
1.2 气象观测站点数据
台站数据被认为是地面气温的真值,被用于气温估算模型的训练和验证。使用湖南省2020年的97 个国家级自动气象站的逐小时地面气温数据进行研究(http://data.cma.cn)。这些气温数据经过了包括气候学界限值、区域界限值、时间一致性及空间一致性检查等在内的严格质量控制,可用率达98.9%[25]。湖南省的海拔和其97 个台站分布如图1所示。表1 总结了主要数据的特征,包括数据的时空分辨率和来源。
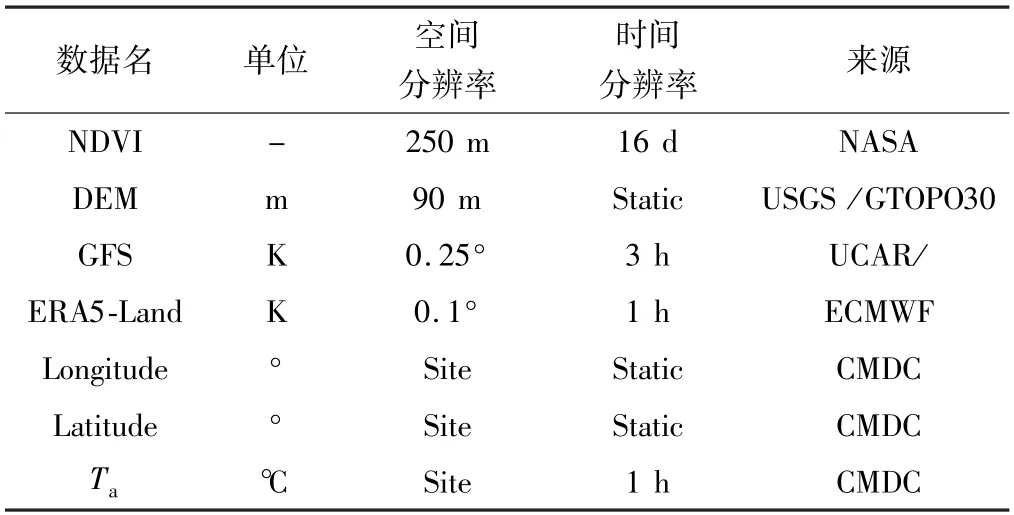
表1 数据的时空信息及来源
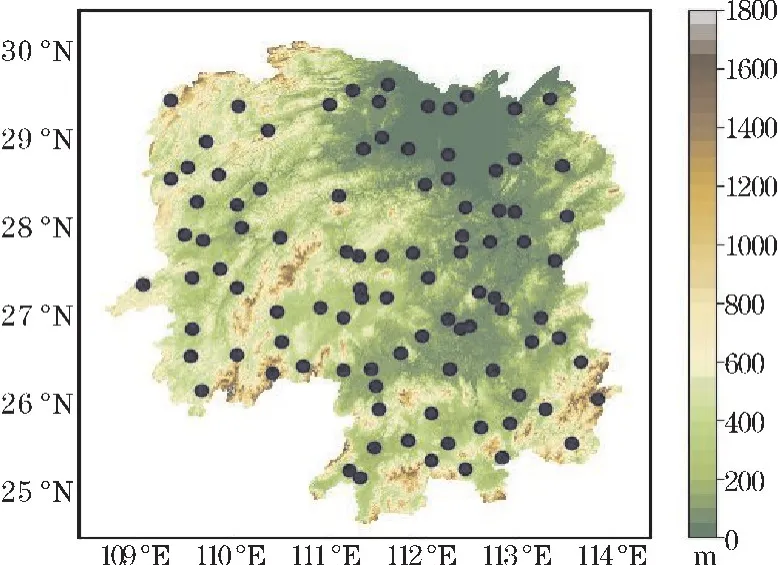
图1 研究区域海拔和气象台站位置空间分布图
1.3 GFS
美国国家环境预测中心(NCEP)运营的GFS 在全球范围内提供0.25°、0.5°和1°网格化气温数据。网格包括分析和预测时间步长,0~240 h是预测时间步长为3 h的网格数据,240~384 h是预测时间步长为12 h的网格数据,模型预测运行在每天00、06、12 和18UTC进行。
本研究使用2020年分辨率为0.25°的GFS 预测气温。美国国家大气研究中心(NCAR)的研究数据档案(RDA)拥有NCEP GFS 0.25°全球预报网格(https://rda.ucar.edu/datasets/)的完整历史档案。RDA 提供了一个子集工具,用于通过可自定义的数据请求选择变量、时间和区域,使其易于下载和使用气温预测。GFS 气温预报是通过https://rda.ucar.edu/datasets/ds084.1 使用可定制的数据请求下载的。实时GFS 气温预报可从NOAA NCEP(https://www.nco.ncep.noaa.gov/pmb/products/gfs/)获得。
1.4 ERA5_Land 数据
为更好地验证DS 模型的结果,使用ERA5-Land再分析数据进行比较。ERA5-Land 是新一代的再分析和同化数据,比以前的版本具有更好的时空分辨率和准确性[26-27]。
ERA5-Land 提供每小时气温数据,网格大小为0.1°×0.1°,通过重播ECMWF ERA5 气候再分析的土地部分而制作。通过使用物理定律,重新分析将模型数据与来自世界各地的观测结果组合成一个全球完整且一致的数据集。ERA5-Land 数据通过https://climate.copernicus.eu/the-climate-data-store 下载。
1.5 其他辅助数据
研究表明,海拔、纬度、NDVI、JD 和小时数据等辅助数据可以提高气温降尺度的精度[28-32]。使用航天飞机雷达地形任务(SRTM)的高程数据集,分辨率为3 弧秒(~90 m)。SRTM3 数据从ftp://e0srp01u.ecs.nasa.gov/srtm/version2/SRTM3/下载。
纬度和时间信息取自AGRI 地理位置数据,并使用中分辨率成像光谱辐射计(MODIS)的16 天植被指数产品(MOD13Q1)。MOD13Q1 NDVI 产品的空间分辨率为250 m。数据来自土地处理分布式活动存档中心(LP DAAC;https://lpdaac.usgs.gov/)。
2 方法
目前,一般降尺度方法都是基于大气温度垂直递减率理论(ALR)开展的。垂直递减率是气温通常随着高度的升高而下降,下降速度约为5~6 ℃/km,一般公式如下:
Ta=T-ALR×(H-H0)
式中,H0是高分辨率的海拔数据,T是低分辨气温,H是低分辨率的海拔数据,Ta是高分辨率气温。但考虑到夏季垂直递减率更为显著,对其他季节的适用性有待进一步验证。所以选用神经网络来构建气温与预测因子间的映射关系。神经网络是由多个神经元构成的非线性模型,能够更好地获取预测变量和输出变量的非线性关系,被广泛应用于气温的降尺度。神经网络能从训练数据集中学习到不同尺度下海拔(ElE)、NDVI 差异所带来的气温差,从而实现高空间分辨率气温模型的构建。DS 模型的结构公式:
Ta=f(GFS,ElE,JD,Hour,Lon,Lat,NDVI)
其中f(·)表示DS 模型需要建模的非线性估计函数。
DS 模型算法可分为3 个部分:数据处理、DS 降尺度模型建立以及降尺度结果的验证和分析。
数据处理。首先,对GFS 数据进行双线性插值处理,将0.25°×0.25°的GFS 数据插值为250 m×250 m的网格数据,再将SRTM 数据从90 m重采样到250 m。空间分辨率为0.25°和250 m的数据分别是粗分辨率和细分辨率中拟合关系的输入参数。利用2020年湖南台站的时空信息采用最近邻域法去匹配对应的GFS、海拔、NDVI 等数据,得到2020年的数据集。经过处理后,总共识别出274301 组样本。根据台站随机划分,将其中约一半的数据用于训练模型,称为训练集,而另一半数据用于验证模型,称为验证集,具体如表2。

表2 训练和验证数据集
模型的建立和应用。模型的建立如图2 红虚线部分:将训练集数据放进神经网络中进行训练,并用验证集数据去验证模型的精度,最终得到DS 模型。应用部分如图2 蓝实线部分:将实时的数据集输入DS 模型,经过模型的输出,最终得到250 m×250 m的近地面气温数据。

图2 算法流程图
降尺度结果的验证和分析。使用相关系数(R)、均方根误差(RMSE)和偏差来评估降尺度模型的准确性,如下所示:
式中,Ta是降尺度的气温,Tsta是气象站观测到的气温,N是数据样本的总数。
3 结果讨论
3.1 总体误差分析
图3 为降尺度模型验证与台站气温的二维直方图,降尺度的气温(DSTa)与台站观测气温(In-situTa)吻合度较好。DS 的均方误差为1.54 ℃,相关系数为0.982。平均偏差为-0.03 ℃,表明降尺度气温整体没有明显的高估或低估。总的来说,结果表明该模型在缩小温度数据方面表现良好。
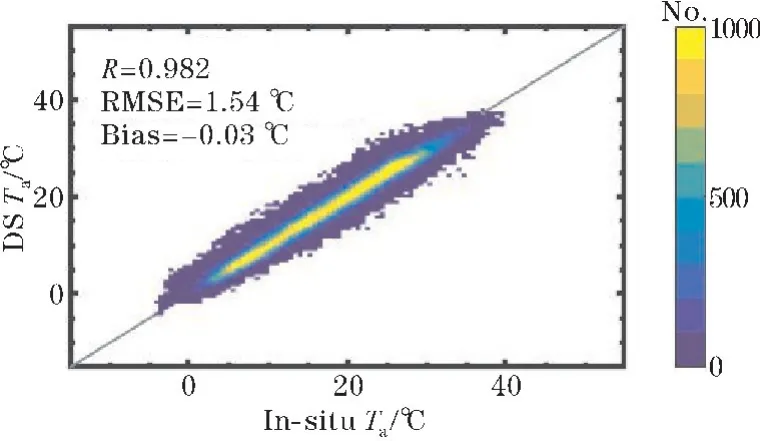
图3 DS Ta 与In-situ Ta 的二维直方分布图
图4 显示了模型的Ta降尺度误差(DS-In-situTa)的垂直分布。DSTa的误差呈正态分布,大多数误差在±2.5 ℃(>80.92%的样本)。DSTa误差小于±1.5 ℃的数据点占63.55%。这意味着DS 模型是可行的。

图4 DS Ta 和In-situ Ta 之间的差异直方图
3.2 误差时空分析
为进一步评估该模型在湖南地区的适用性,本文逐个站点评估了降尺度气温的误差。图5 为模型的R、RMSE 和Bias 的空间分布图。总的来说,模型的所有站点都表现较好。R在0.974~0.994,这表明估算气温和台站实测气温相关性较高;RMSE 在1.05 ℃~1.99 ℃,Bias 在±0.5 ℃以内,表明DS 模型有较高的精度。
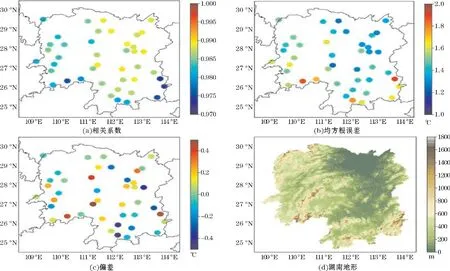
图5 模型的R、RMSE 和Bias 的空间分布图
DS 的误差展现了一定的空间分布特征。从图5可以看出,位于湖南省边界的台站展现了较大的RMSE 和较小的R,通过和湖南地形图比较,发现这些站点的海拔较高。这种误差空间分布特征可能是由高海拔地区通常地形较为复杂,导致温度垂直递减率在空间和时间上有所不同[33]。通常情况下,山区的垂直递减率比平原地区复杂[34-35]。
表3 给出了两种数据集(GFS 和DS)在不同海拔处的验证结果,可以看出,DS 在各个海拔都对GFS 数据有着很好的订正效果。GFS 数据在各个海拔上都呈现出明显的负偏差,在400~600 m的海拔范围内的Bias 达到了-1.9 ℃,而DSTa的偏差不超过±0.2 ℃。在各个海拔段里,DSTa比GFSTa有着更小的RMSE,且DSTa也比较稳定,RMSE 稳定在1.48 ℃~1.67 ℃。这意味着DS 能够很好的处理不同海拔下的气温数据。
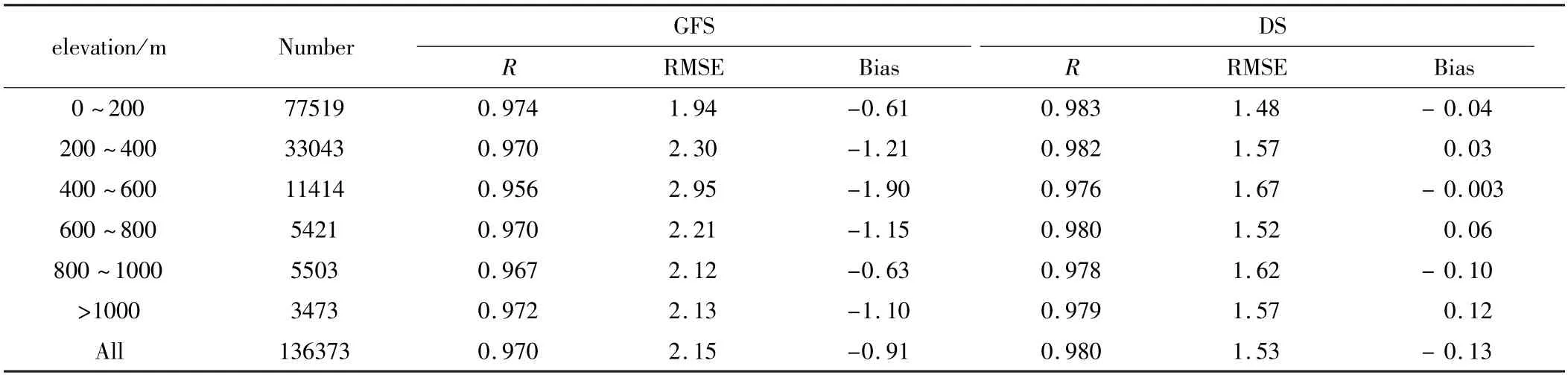
表3 不同高程间隔的GFS 和DS 的误差分析
作为示例,图6 为2021年6 天(即DOY 10、69、130、191、253、314)的GFS 原始数据、ERA5-Land 和DS 气温分布图。图6 可以发现,DSTa显示了更多关于气温的细节,尤其是在南部和西部有许多山脉,其对应位置的气温都较低。虽然GFS(0.25°)和ERA5-Land(0.1°)的气温可以呈现整个区域的气温空间模式,但粗分辨率不能满足在局部尺度上绘制气温的要求。DSTa(250 m)可以清晰地反映气温的空间分布。图6 表明,降尺度前后和ERA5-Land 的气温图像在尺度上非常相似,包括幅度和空间细节:中部和东北部因海拔较低而偏暖,而西部和南部因海拔较高而较冷(海拔见图1)。总的来说,这3 个数据集的空间分布和温度梯度非常相似,都显示出相似的季节性气温动态。但DS 空间分辨率高(250 m×250 m),相比于ERA5-Land(0.1°×0.1°)和GFS(0.25°×0.25°)能展现更多的空间细节。图7 为图6 中6 个时刻的误差散点分布图,从图7 DSTa与GFSTa和ERA5Ta对比发现,DSTa更集中,GFSTa和ERA5Ta较为发散。DSTa的RMSE 为1.674 ℃,而GFSTa和ERA5Ta的RMSE 为2.867 ℃和2.772 ℃,这表明DS 还能提高GFS 气温的精度。
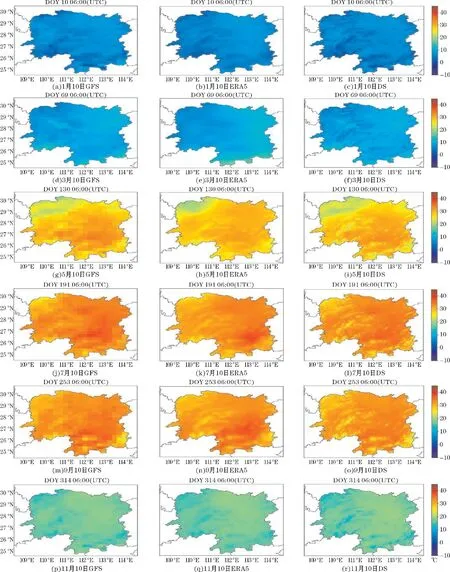
图6 2021年1、3、5、7、9、11月10日6 UTC 时刻的GFS、ERA5-Land 和DS 气温空间分布图
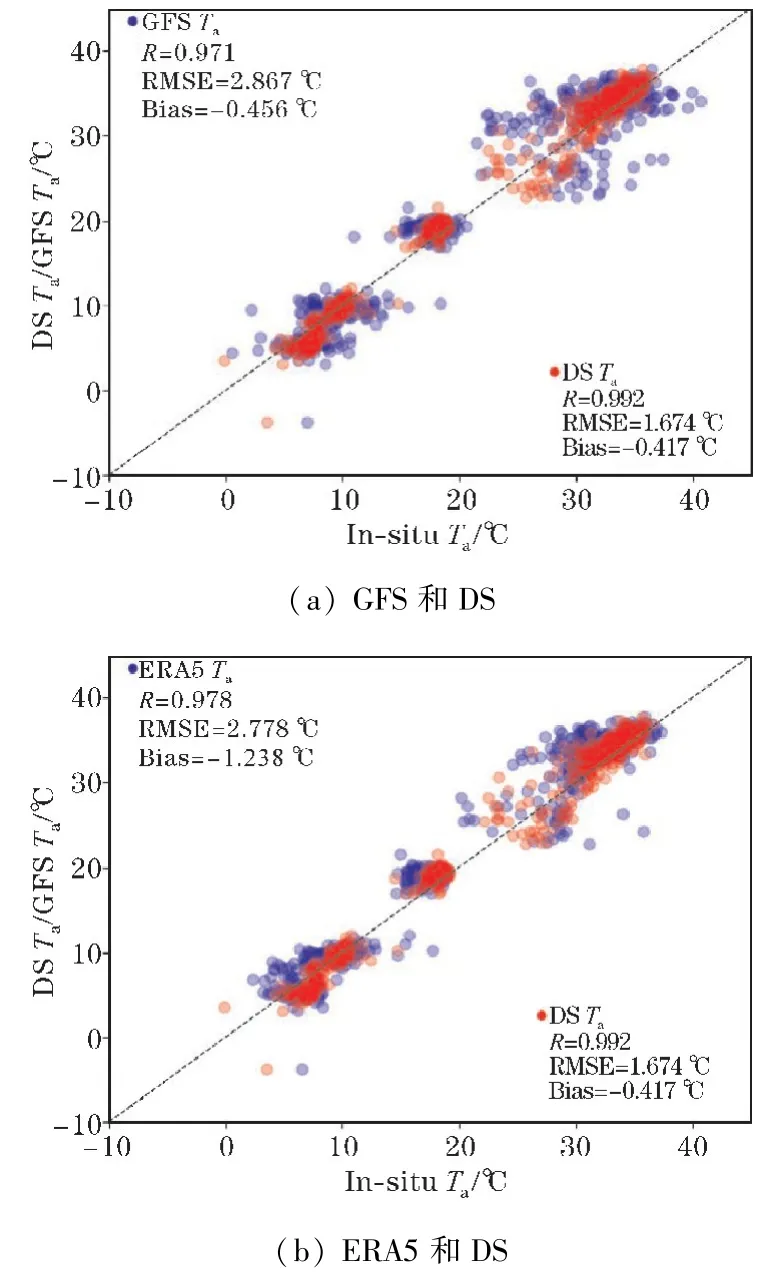
图7 6 个时刻的散点对比图
3.3 影响降尺度因数分析
本研究假设影响DS 的是地表特征和时间,如海拔和JD。基于上述97 个气象站的瞬时Ta,通过以下方法对该假设进行检验。以所有输入的因素为自变量进行网络训练模型;测试了可能因素的不同组合,包括案例1:海拔;案例2:海拔和时间;案例3:海拔、时间和纬度;案例4:海拔、时间、纬度和经度;案例5:海拔、时间、纬度,经度和NDVI。海拔被选为主要因素,因为Ta随着海拔的升高而降低,尤其是在山区。纬度和经度代表位置和太阳角,时间代表季节性和白天黑夜,使用NDVI 来参数化植被覆盖率。气温还受到其他地表特征的影响,如土壤水分和降水[36]。然而,本研究未考虑土壤水分和降水,因为当前产品具有粗糙的空间分辨率和时间分辨率[37-38],且无法满足气温的降尺度要求。各个案例的RMSE 如图8所示,案例1 和2 中的海拔和TIME 解释了整个研究区域内Ta空间变化的主要内容。当DS 模型中仅包含海拔和时间时,RMSE 的增量在0.3 ℃~1.4 ℃,因此,海拔和时间可以作为Ta降尺度的主要因素。如Li 等[39]还发现纬度也会影响Ta的空间变化。但对于97 个台站而言,纬度、经度和NDVI 对气温空间变化的贡献是可忽略的:在案例3、案例4 和案例5 中,RMSE 的最大增量<0.15 ℃。这些不同数据集组合的模型精度证实了在模型中融合多源数据在气温降尺度中实际上是有意义的。另一方面,当使用更多数据集时,映射结果将在空间上以更详细的信息进行优化。
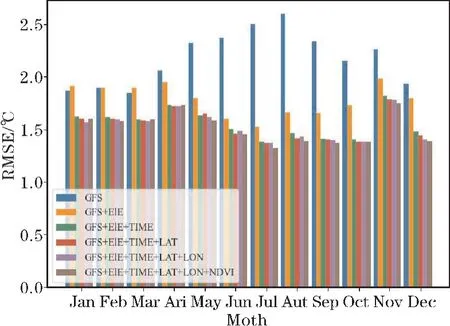
图8 Ta 与研究区不同因子线性回归中的RMSE
4 结论
在气候变化、水文、生态学等研究中,气温是一个重要的参数。然而,目前气温产品的粗空间分辨率已不能满足相关研究和应用日益增长的需求,如GFS,ERA5 等。本研究以中国湖南省为研究区域,提出一种将GFS 提供的气温数据集从粗分辨率(0.25°)降为高分辨率(250 m)的神经网络降尺度方法。
首先根据97 个气象站对DSTa的精度进行评价。结果表明:从GFS 产品降尺度后,97 个站点的气温均方根误差为1.53 K;与降尺度前的气温相比,降尺度后的气温与地面实测的气温有更好的一致性。此外,从图像质量的角度对DSTa图像进行评价,整体空间分布情况大致相同,降尺度后的气温图像具有良好的图像质量,能够清晰地反映山区气温的空间变化。与现有的气温降尺度方法相比,本文方法的机理不依赖地面实测数据,因此,可以更容易地应用于大面积地区。本研究仅使用了国家标准气象站,未来可以引入更多的区域气象站来提高降尺度精度。

