复杂下料工艺约束下的二维不规则零件优化排样方法
吴电建 张三强 杨光友
1.湖北工业大学农机工程研究设计院,武汉,4300682.湖北省农机装备智能化工程技术研究中心,武汉,430068
0 引言
二维不规则零件的下料问题属于典型的NPC问题[1-2]。目前,二维不规则零件优化排样方法已有较多的研究成果。文献[3-4]用不规则零件图形的外接包络矩形替代其外形轮廓来降低零件图形定位的计算复杂度,快速获得排样方案,但这种方法易造成大量碎化废料,导致原材料利用率不高。文献[5-6]借助图形栅格技术实现不规则零件图形的像素化表达,通过栅格占空来描述零件图形轮廓,但这种方法受限于图形轮廓大小和像素精度尺寸,且算法计算的内存开销大,难以保证时间效率。为保留零件图形轮廓特征,文献[7-8]引入临界多边形算法来实现零件图形间位置关系向点包含关系的转换,但随着零件数量和旋转角度的增多,算法复杂度增加,计算时间延长。文献[9-10]提出的零件图形间碰撞检测算法可快速完成零件定位,但算法易陷入局部优化,导致排样方案的原材料利用率波动较大。上述优化排样方法针对原材料、二维不规则零件等常见约束,寻找原材料利用率更高的排样方案,但这些排样方案中的零件杂乱排布。为满足原材料自动送料、机床连续切割、零件自动码垛等复杂下料工艺约束,需人工调整部分零件位置来构造出零件按某种规律排布的排样方案,导致现有二维不规则零件下料生产线出现原材料利用率不高、作业效率较低等问题。因此,为在提高原材料利用率的同时,保证机床连续切割和零件自动码垛的作业效率,本文针对下料生产线的复杂下料工艺约束开展二维不规则零件优化排样研究。
1 问题描述和数学建模
1.1 问题描述
图1所示为下料生产线上二维不规则零件下料的主要生产流程及优化排样方法。下料生产线通过原材料自动送料、机床连续切割和零件自动码垛,实现零件的自动分离和库存。
图1中,下料生产线的3种加工设备及其工序如下:工序1,送料整平机完成金属卷材的自动送料、拉直和整平,为后续工序提供原材料;工序2,数控切割机床在指定加工区域内连续切割,使所需零件从金属板材上分离;工序3,自动码垛机定时定点抓取已分离的零件,并将其转移到临时库存区内,实现零件的自动码垛。
上述3道工序的下料工艺约束给出了二维不规则零件下料的优化排样方法及其主要步骤:
(1)分析并提取原材料、二维不规则零件和下料工艺等约束信息和下料生产优化目标,建立下料生产线的二维不规则零件下料问题数学模型。
(2)针对该模型设计一种基于排样单元的优化排样算法,构造满足上述所有约束条件的多种排样方案,并基于最大化原材料利用率,优化得到本次送料整平机上的卷材规格和对应的排样方案。
(3)基于优选出的排样方案拆分出对应的重复单元,计算出自动码垛机抓取零件的位置点和数量等数据信息。通过优化排样方法构造的排样方案智能决策并控制下料生产线的主要生产流程。
1.2 数学建模
1.2.1符号定义
数学模型中所使用到的变量符号定义如表1所示。

表1 变量符号表
1.2.2数学模型
基于对下料生产线上二维不规则零件下料问题的描述,建立该类问题的数学模型:
(1)
s.t.Wc=Wj
(2)
Lc=Sright_x
(3)
mbi≥di
(4)
Ωu∩Ωv=∅u,v=1,2,…,n
(5)
∀Ωi∈Ω(Lc,u,Wc,u)
(6)
Lc-lleft=Lc,u
(7)
Wc-2wleft=Wc,u
(8)
Ωi+δ=Ωi,u
(9)
S=mU
(10)
其中,式(1)表示最大化原材料利用率f(S)为优化目标;式(2)、式(3)是原材料约束,分别表示本次下料生产可选的卷材宽度和所需的卷材长度;式(4)是零件约束,表示本次下料得到的每种零件量满足零件的需求量;式(5)是零件约束,表示任意2个零件的图形轮廓不能相交;式(6)是原材料和零件间的关联约束,表示所有零件图形轮廓必须在原材料区域内;式(7)、式(8)表示为保证零件从原材料的顺利切割分离,应通过预留原材料边界实现贴边零件的切断;式(9)表示机床刀具切割应预留出刀具厚度的等距量,以保证机床切割加工得到的零件尺寸精度;式(10)表示任意一种排样方案均由m个排样单元组成,通过构造重复的排样单元来满足机床连续切割加工和零件自动码垛的工艺约束。
2 优化排样算法设计
2.1 图形预处理
为满足下料生产线机床切割加工的工艺约束即式(7)~式(9),在排样设计时对当前下料卷材和零件的图形进行预处理,如图2所示。在卷材图形长度、宽度方向上分别增加留边量lleft和wleft,获得当前卷材的可排样区域即图2a中的红色区域;在每种零件图形轮廓上增加搭边量δ,得到该零件在卷材上排样时的真实图形轮廓即图2b的红色区域。
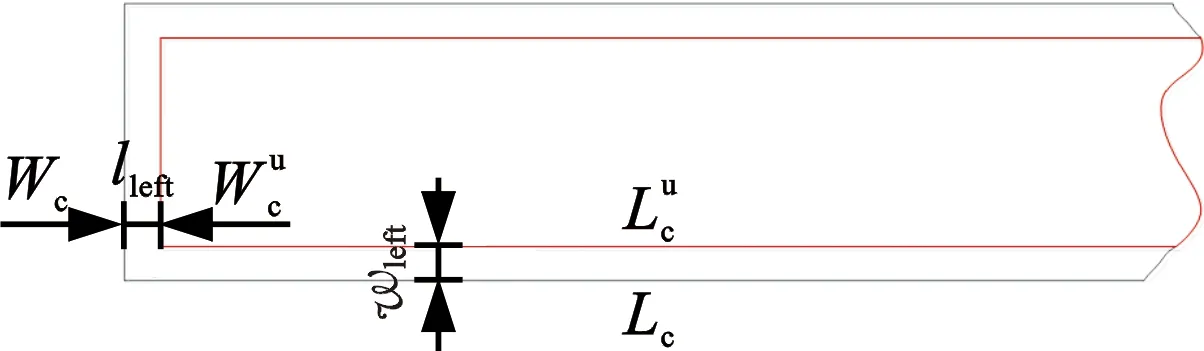
(a)卷材可排样区域
2.2 零件图形间碰撞算法
为满足零件图形互不相交的约束(式(5)),实现零件间的定位,并保证零件排样的紧密性,基于冲裁件碰撞算法[11-12]设计了一种零件图形间碰撞算法,具体流程如图3所示。算法主要步骤如下:
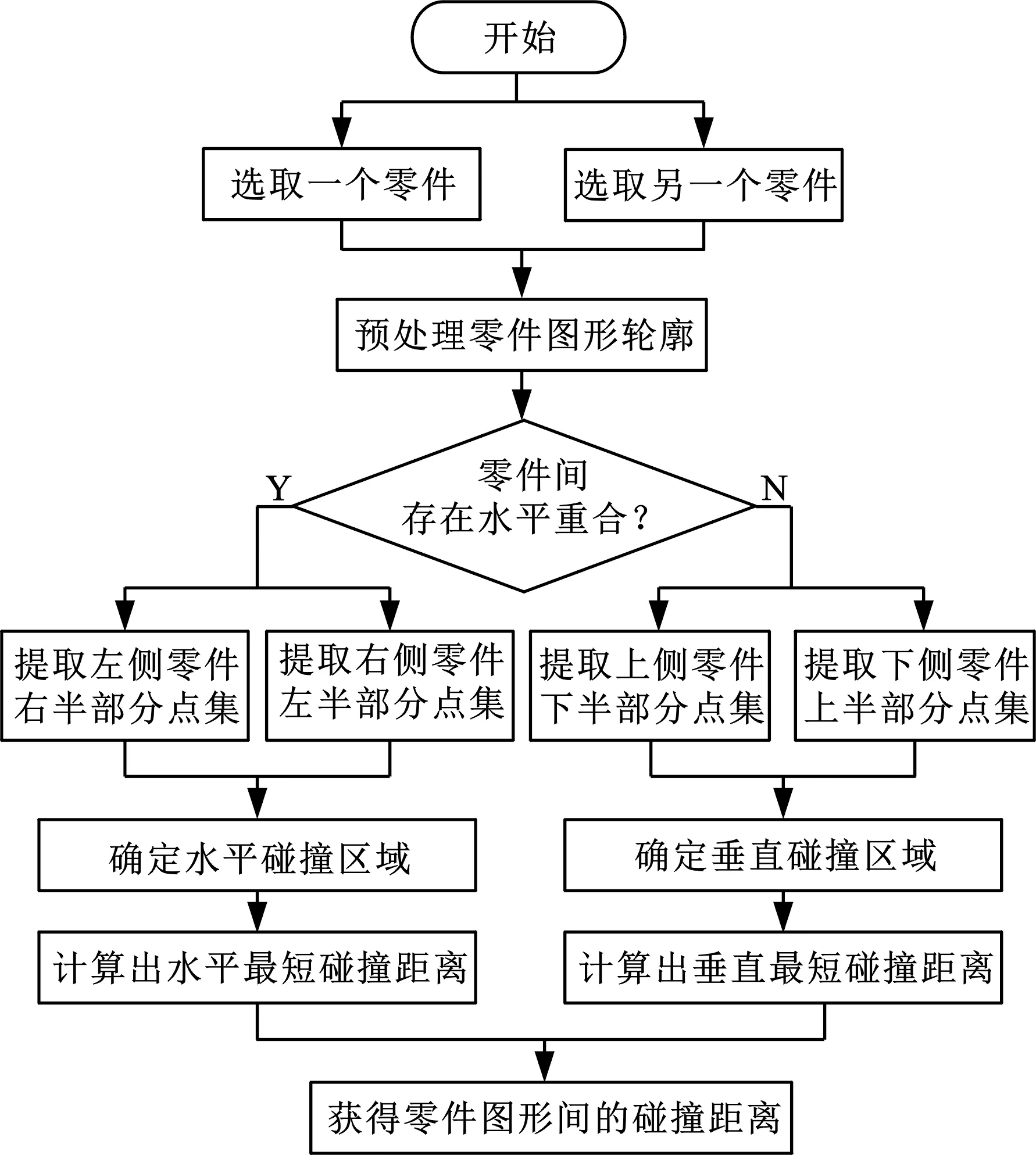
图3 零件图形间碰撞算法流程图
(1)选取2个待排样的零件,预处理它们的图形轮廓,得到其真实碰撞轮廓。
(2)基于零件的初始位置关系判断零件间是否存在水平重合,若存在,转到步骤(3);若不存在,转到步骤(8)。
(3)如图4a所示,在水平碰撞示意图中,先提取左侧零件右半部分点集{pl,1,pl,2,…,pl,n},其中,pl,1、pl,n分别为左侧零件点集中纵坐标最大的点和纵坐标最小的点。

(a)水平碰撞 (b)垂直碰撞
(4)再提取右侧零件左半部分点集{pr,1,pr,2,…,pr,n},其中,pr,1、pr,n分别为右侧零件点集中纵坐标最大的点和纵坐标最小的点。
(5)将点pl,1和点pr,1中纵坐标较小的点作为碰撞区域最高点pr,1,将点pl,n和点pr,n中纵坐标较大的点作为碰撞区域最低点pr,n。
(6)以最高点pl,1和最低点pr,n为起点,向对侧零件轮廓做水平射线,得到交点pr,e和pl,e,确定水平碰撞区域pl,1pl,epr,npr,e。
(7)在水平碰撞区域内,分别计算左侧碰撞点集{pl,1,pl,2,…,pl,e}中每个点到右侧零件轮廓的水平距离和右侧碰撞点集{pr,e+1,pr,e+2,…,pr,n}中每个点到左侧零件轮廓的水平距离,将最短水平距离作为零件间的水平碰撞距离,并转到步骤(13)。
(8)如图4b所示,在垂直碰撞示意图中,提取上侧零件的下半部分点集{pu,1,pu,2,…,pu,n},其中,pu,1、pu,n分别为上侧零件点集中横坐标最大的点和最小的点。
(9)提取下侧零件上半部分点集{pd,1,pd,2,…,pd,n},其中,pd,1、pd,n分别为下侧零件点集中横坐标最大的点和横坐标最小的点。
(10)将点pu,1和点pd,1中横坐标值较小的点作为碰撞区域最右点pu,1,将点pu,n和点pd,n中横坐标值较大的点作为碰撞区域最左点pd,n。
(11)分别以最右点pu,1和最左点pd,n为起点,向对侧零件轮廓做垂直射线,得到交点pd,e和pu,e,确定垂直碰撞区域pu,1pu,epd,npd,e。
(12)在垂直碰撞区域内,分别计算上侧碰撞点集{pu,1,pu,2,…,pu,e}中每个点到下侧零件轮廓的垂直距离和下侧碰撞点集{pd,e+1,pd,e+2,…,pd,n}中每个点到上侧零件轮廓的垂直距离,选取最短垂直距离作为零件间的垂直碰撞距离。
(13)获得2个零件图形间的碰撞距离。
2.3 排样单元构造方法
为满足下料生产线机床连续切割和零件自动码垛的约束条件(式(10)),基于2.2节提出的零件图形间碰撞算法,通过零件图形的平移、旋转、镜像等操作实现多个零件的动态组合,构造多种排样单元,如图5所示。针对待排样的零件,利用平移矩阵使零件图形水平方向平移Δx、垂直方向平移Δy后,得到由2个零件组合而成的一种排样单元,如图5a所示;零件图形平移和旋转后,得到一种排样单元,如图5b所示;零件图形平移、旋转、水平镜像、垂直镜像后,得到两种排样单元,如图5c所示。因此,通过控制零件图形平移量、旋转角度和镜像方向可得多种排样单元,不同排样单元可组合成多种排样方案。

(a)零件图形平移变换 (b)零件图形旋转变换 (c)零件图形镜像变换
排样单元处理机床连续切割和零件自动码垛等复杂下料工艺约束的实现方法如图6所示。针对卷材宽度和零件需求量两种约束,基于上述排样单元设计一种优化排样算法,计算排样单元内的决策变量(Δx,Δy,α)和排样单元间的决策变量(x,y,m),得到由排样单元组合而成的排样方案。该排样方案可拆分出机床连续切割单元,快速指导数控机床在板材上连续切割加工;计算出自动码垛每次需抓取单元的个数,控制码垛机自动抓取固定位置点上已切割分离的多个零件。基于排样单元构造的排样方案适用于机床连续切割和零件自动码垛的工艺约束,提高下料生产的作业效率。

图6 排样单元处理复杂下料工艺约束的实现方法
2.4 基于排样单元的二维不规则零件优化排样算法
为构造高利用率的卷材排样方案,并满足下料生产线的复杂工艺约束,设计了一种基于排样单元的二维不规则零件优化排样算法,其流程如图7所示。初始化多种卷材和二维不规则零件图形和数据信息,利用2.1节介绍的方法预处理待下料的卷材和零件图形后,得到卷材可排样区域和零件实际排样轮廓;结合2.2节提出的零件图形间碰撞算法和2.3节设计的排样单元构造方法,设计出多种排样单元,满足下料生产线的工艺约束,简化下料问题的复杂度;针对每种规格的卷材,以卷材左下角为排样起点,依次利用每种排样单元在卷材宽度方向进行排布,再沿卷材长度方向进行重复排列,直到满足零件需求量为止。以最大化卷材利用率为优化目标,通过设计的优化排样算法搜索、迭代和寻优后,找出一种排样方案,并确定当前下料所需的卷材规格。

图7 基于排样单元的二维不规则零件优化排样算法流程图
3 算例验证
某企业生产线常见的8种下料零件的数据如表2所示。假设卷材留边值为5 mm,零件搭边值为2 mm;该企业通常存放宽度0.8 m、1.0 m和1.2 m的卷材。通过算例对比分析不同优化排样方法构造的排样方案对应的卷材利用率来验证所提方法的可行性和有效性。

表2 8种下料零件数据信息
结合下料生产信息,分别利用本文提出的优化排样方法、文献[2]的优化排样算法和商用软件FormingSuite在指定规格卷材上进行零件优化排样设计。3种方法针对每种零件构造的排样方案的卷材利用率如表3所示。

表3 不同排样方案的卷材利用率
在表3中,加粗的数字表示本文方法的卷材利用率高于另外两种方法的卷材利用率。对比分析表3横向数据可知,本文方法在3种宽度卷材上进行零件排样时的卷材利用率多数都高于另外两种方法;分析表3纵向数据可知,本文方法在同一宽度卷材上进行零件排样设计时的卷材利用率多数都高于另外两种方法;对于所有零件,本文方法在3种不同宽度卷材的平均材料利用率均高于另外两种方法。因此,本文方法在处理二维不规则零件下料问题上具有可行性和有效性。
为更加直观地对比3种方法的排样效果,表4给出了表2中的零件1在3种宽度卷材上的排样方案。本文方法在宽度0.8 m和1.2 m卷材上的利用率均高于另外两种方法;在宽度1.0 m卷材上的利用率略低于商用软件FormingSuite,但高于文献[2]的排样算法。在排样方案上,本文方法考虑多种工艺约束,构造出更多的排样单元,增加了二维不规则零件在卷材上的排样方案,提高了排样解质量。
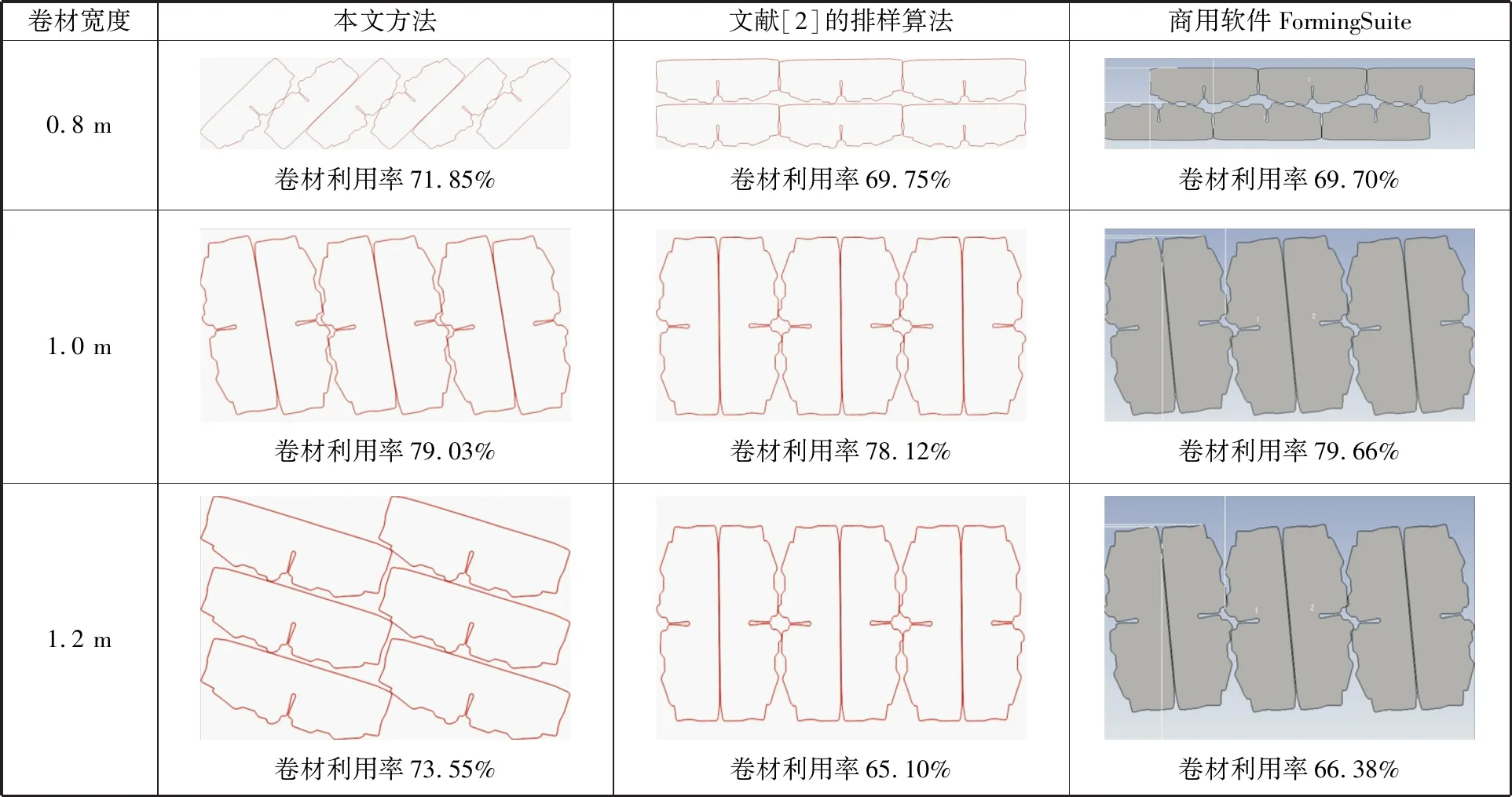
表4 零件1在3种宽度卷材上的排样方案
4 结论
(1)以图形预处理技术和零件图形间碰撞算法为基础,引入排样单元构造方法,得到了满足机床连续切割和零件自动码垛等复杂下料工艺约束的排样单元。
(2)8种二维不规则零件的优化排样算例结果表明,本文方法构造的排样方案的卷材利用率多数高于已有算法和商用软件,具有可行性和有效性。

