基于DGR 技术处治桥头跳车沉降预测研究

孙 董，谷 健

（中国市政工程西南设计研究总院有限公司，四川 成都 610081）

0 引言

运营期国省道往往交通量较大，由于桥台路基处刚性与柔性沉降不均，易产生沉降差导致桥头跳车现象产生，因此现通过宁波地区的一座桥头过渡段处采用DGR 技术（深层注浆加固抬升技术（Deep Grouting Reinforcement，以下简称DGR）[1]，

DGR 技术对于处治运营期公路的桥头跳车效果非常好，吴承霞[2]通过运用DGR 技术治理软基研究表明，治理后的软基承载力得到了一定的提升及沉降量得到相应控制。深层注浆技术后的土层形成一层帷幕，阻止水的侵蚀，同时浆液与土体形成整体地基，承载力得到大幅提升，具有较高的稳定性[3-5]。

现通过宁波镇海区K178+928 处洪家桥采用DGR 技术来进行桥头跳车处治后的沉降预测研究。

1 DGR 技术理论与应用

宁波市镇海区的G329 国道上K178+928 洪家桥，其桥头过渡段现场运用DGR 技术，如图1 所示。

图1 DGR 工艺现场注浆之实景

通过浆液的渗透、压密、填充，与土体缓和后，浆液凝固后，与土体一起成为有效的整体组合，土体的整体性与承载力得到提高，且密实性较高，有效地防止地下水的侵蚀，经过固结后，最终形成强度高、稳定性好、刚度大的复合地基，能够有效地减少路基沉降[6-9]。

DGR 技术可以在公路运营期间，避免公路大幅开挖，周期短、见效快、实用性较高。

2 DGR 技术曲线拟合法模型分析

路基沉降预测有各种各样的方法，现采用常用的双曲线模型和指数曲线模型[10]，通过相应的模型公式，结合现场沉降数据代入后获得相应参数经过公式进行沉降预测（见表1）。

表1 曲线模型表

对于检测曲线模型预测沉降的正确性，可引用相关系数来验证：

式中：yi为实测沉降值；y0为实测沉降平均值；y'i为计算沉降值。R2称为标准差，用来衡量所配的曲线与沉降观测值拟合的好坏，它的平方根R 称为相关系数。R2和R 愈大（愈接近1），则表明曲线回归效果愈好[11]。

3 DGR 技术沉降曲线模型预测

位于镇海区国道G329K178+928 处洪家桥现状为四幅路，断面如图2 所示。

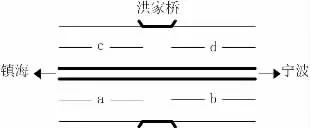
图2 洪家桥各断面位置图

在进行DGR 技术处治后，通过对现状后续的沉降数据实测得到实测沉降曲线，同时对道路中心沉降数据通过指数曲线模型和双曲线模型拟合断面a、b、c、d 的沉降曲线，如图3 所示。

图3 洪家桥断面沉降预测曲线图

经双曲线模型、指数曲线模型计算，通过拟合方程计算，同时算出相关系数，具体计算结果如表2、表3 所列。

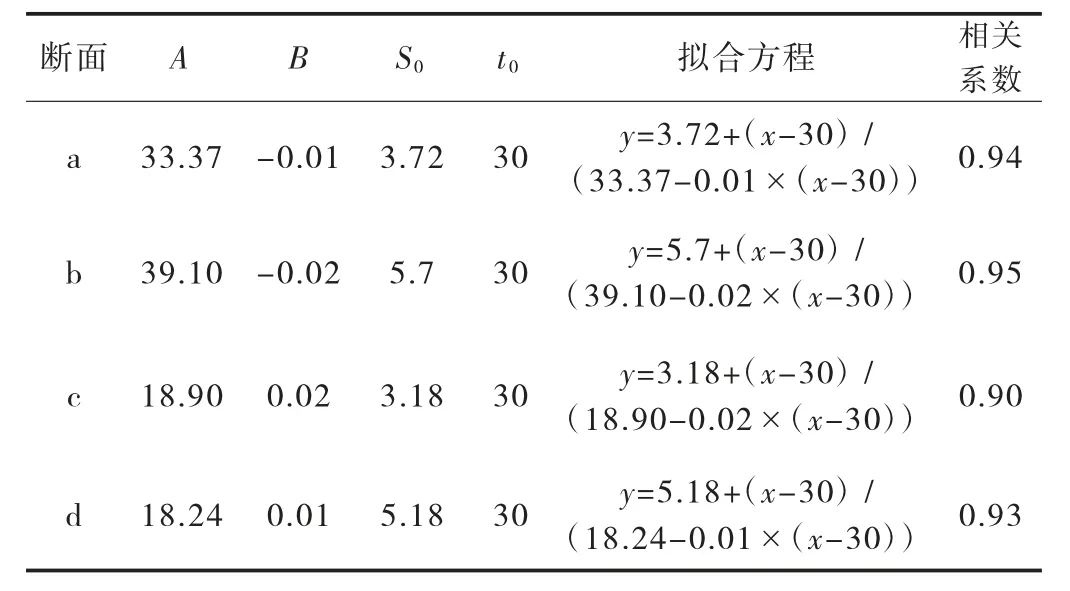
表2 洪家桥各断面双曲线模型相关参数及方程一览表

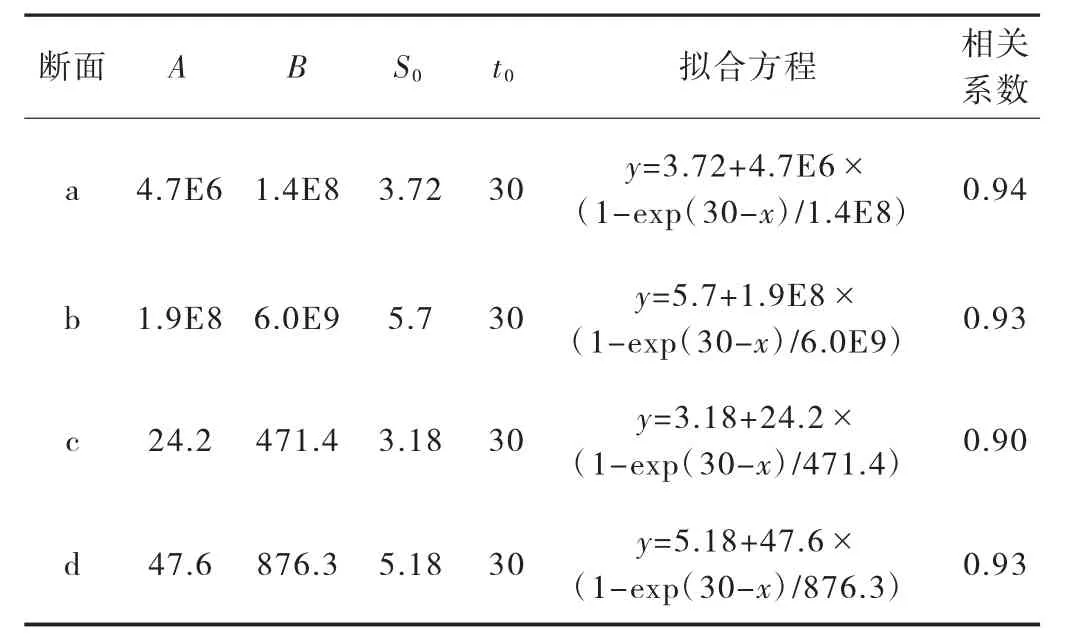
表3 洪家桥各断面指数曲线模型相关参数及方程一览表

通过计算结果可知，指数曲线模型或者双曲线模型拟合方程相关系数均大于0.9，计算结果表明这两种曲线模型均适合拟合洪家桥路桥过渡段沉降预测。

4 桥头断面沉降发展规律分析

洪家桥在经过DGR 技术处治路桥过渡段后，经过后续时间的沉降数据实测，得出所经时间与沉降关系实测关系，如图4 所示。

图4 桥头断面时间沉降关系图

通过以上各桥头断面时间沉降关系图可知，各断面沉降曲线大致相同有些许差异，总趋势大概一致，在90-120 d 时间段里沉降速度较快，后续沉降逐渐稳定，在450 d 处最大累计沉降各断面为18～24 mm 之间，总体来说沉降较小，处治效果较好。

5 DGR 方法预测沉降分析

通过前述计算参数代入双曲线模型及指数曲线模型，可得洪家桥在DGR 技术处治下的最终沉降量值，洪家桥桥头预测的最终沉降量如表4 所列。

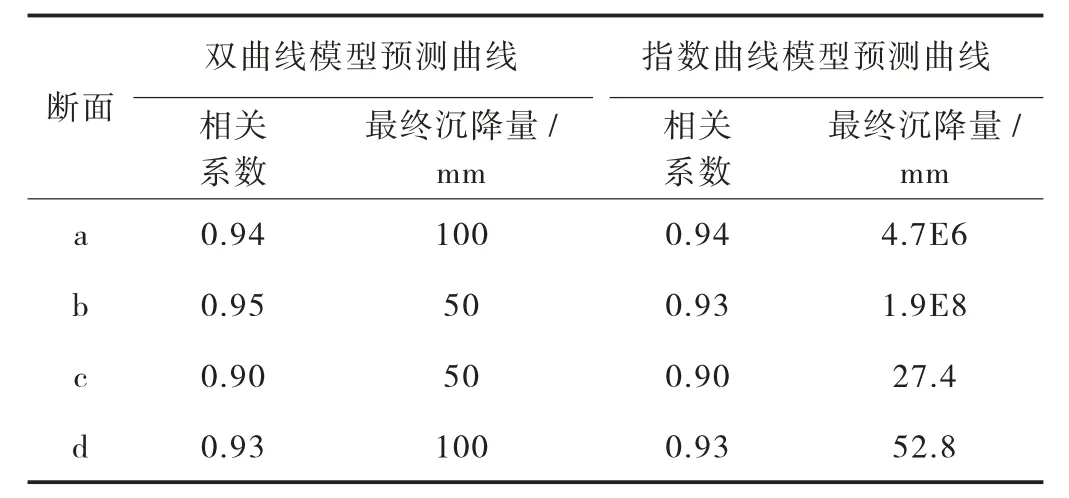
表4 洪家桥桥头预测最终沉降量一览表

从表4 可知，双曲线模型及指数曲线模型预测沉降结果差异较大，a 和b 断面的指数曲线模型预测结果明显不符合实际情况，相对来说运用双曲线模型预测沉降更为合适，经双曲线模型预测最终沉降为50～100 mm。

指数曲线模型预测最终沉降不合适可能由于在DGR 技术处治后投入运营期时，刚开始的沉降还未稳定，以及监测点较少导致。

6 结论

通过对洪家桥路桥过渡段采用DGR 技术处治后，对后续沉降采用双曲线模型及指数曲线模型进行沉降预测研究，得出以下结论：

（1）DGR 技术处治桥头跳车病害，从实测沉降数据来看治理效果较好。

（2）洪家桥桥头的实测曲线拟合与双曲线模型、指数曲线模型拟合相关系数较高。

（3）对于路桥过渡段的后续沉降预测，双曲线模型相比指数曲线模型更适合。

（4）根据沉降预测，洪家桥桥头的最终沉降量为50～100 mm。