基于无人机点云与改进RS表征法的结构面粗糙度定量分析

杨 泽,李保天,宋盛渊,秦 龙,刘殿泽,黄 迪

(1.吉林大学 建设工程学院,长春 130026;2.中铁三局集团第六工程有限公司,山西 晋中 030600;3.贵州省交通规划勘察设计研究院股份有限公司,贵阳 550081)

岩体结构面影响着岩体完整性及强度,并使岩体的物理力学性质具有各向异性、非均一性、不连续性等特点[1]。坝体、隧道、高陡岩质斜坡等岩体工程稳定性受到结构面控制,其中结构面粗糙度(JRC)又控制着结构面剪切强度[2-5]。因此,精确测量结构面真实形态并使用相关系数表征结构面粗糙度,对分析岩体稳定性具有重要的工程意义。

岩体结构面数据获取方法主要分为接触式采集和非接触式采集两类[6]。接触式采集包括单排针状轮廓尺[7]、单针自动式轮廓仪等[8-9]。接触式测量装置的精度受到人为及探针直径等因素影响,当测量对象为较软岩体结构面时测量误差较大且只能测量结构面二维剖面信息,不能完整反映结构面真实信息[10]。非接触式采集包括ATS照相量测系统[11]、三维激光扫描法[12-13]、图像摄影法[14-15]等。相比于接触式测量,非接触式采集测量速度快,精度受人为和测量设备影响较小,但在采集过程中存在选址困难、采集范围小、摄影扫描盲区大等缺点[16]。

文献[17]提出岩体结构面粗糙程度可用JRC表示后,结构面粗糙度评价方法便成为工程地质领域热门研究课题之一。目前,结构面粗糙度评价方法可分为二维评价方法和三维评价方法,常见的二维粗糙度评价方法有:起伏角表征法、Z2法、直边图解法等[18-20],然而此类粗糙度评价方法只适用于计算结构面二维剖面线或出露线状结构面,所得结果与结构面真实粗糙度相差较大,存在片面性。因此,学者们推进结构面粗糙度评价方法由二维向三维转变,使结构面粗糙度表征更接近于真实值。目前,常见的三维评价方法有Z2s表征法、RS表征法、光照百分比法(BAP)法、SRv表征法及分形维数表征法等[21-23]。上述表征方法虽可反映结构面的真实粗糙程度,但大多数三维表征法均采用三角单元作为计算基础,在求算过程中,不同的三角剖分方式所得结果存在差异。再者结构面室内重复力学试验技术尚不成熟[24-25],三维粗糙度表征系数如何与JRC建立联系还亟待解决。

岩体结构面粗糙度评价不仅局限于评价方法的研究,不同采样尺寸、采样间距所得到的结构面粗糙度结果亦存在差异。文献[26]开展研究得出结构面粗糙度随着结构面尺寸的增大而增大,并将此现象称为正尺寸效应;文献[27]通过改进后Grasselli法得出随着结构面尺寸和采样间距的增大,结构面粗糙度逐渐趋于稳定的结论,认为结构面粗糙度存在尺寸效应和间距效应;文献[28]使用Z2s法研究认为随着采样间距增大结构面粗糙度系数逐渐减小。除此之外,相关学者还提出结构面粗糙度正尺寸与负尺寸联合尺寸效应、无尺寸效应等。以上研究工作为结构面尺寸效应与间距效应研究进行了有益的探索,但尚未得出定论。

鉴于此,本文对EI-Soudani提出的RS表征法进行改进,更为准确地表征了结构面真实形态信息。在此基础上,结合无人机多角度贴近摄影测量技术,以察达地区高陡岩质斜坡结构面为研究对象求解表征结构面粗糙度的RS表征值,并深入探讨不同三角剖分方式对RS表征值的影响以及结构面粗糙度尺寸效应及间距效应规律。

1 研究区概况

本文以藏东南某铁路察达工点左岸高陡岩质斜坡结构面为例,开展结构面粗糙度尺寸效应、间距效应的研究。研究区位于西藏自治区昌都市洛隆县南部腊久乡八美村,山脉呈北西-南东走向,全区被念青唐古拉山、伯舒拉岭及他念他翁山等山脉所分隔。研究区构造区属于硕般多断裂带,新构造运动主要表现为地壳的垂直抬升。区内坡度较陡,坡体节理裂隙发育(图1(a)),在斜坡坡脚附近可见大量崩塌滚落块石,块石直径可达数米(图1(b))。研究区整体上属于高山峡谷地貌,区内地势总体呈南高北低,海拔高度为2 312～6 427 m,地形起伏大,地势陡峭,切割较深,呈现出“V”形谷(图1(c))。区内岩性主要为花岗岩,属于粗粒花岗岩,且具片麻理,受断裂活动影响,岩体结构破碎,风化程度高。区域内地下水主要赋存类型为第四系孔隙水。区内植被不发育。

研究区坡面倾向约257°,坡角约55°,斜坡岩体节理裂隙发育。其中一条规模较大冲沟切割了左岸岩体,揭示该处应该存在一条规模巨大裂隙,影响着应力分布规律。区内存在3组结构面发育,按走向分类,NW向结构面最为发育,是控制斜坡稳定性的极不利长大结构面。斜坡上方处存在孤石及松弛岩块,孤石直径最大可达数米,由于强烈风化并产生卸荷松弛岩体所形成,其余则是上部崩解掉落的岩块区内。

2 数据采集与处理

2.1 高精度三维模型构建

斜坡三维模型精度直接影响结构面粗糙度系数计算的精准性。因此本文提出基于无人机多角度贴近摄影测量技术构建高陡岩质斜坡高精度三维点云模型并获取结构面点云信息。此方法具有分辨率高,拍摄范围广等优点。利用无人机获取高精度高陡岩质斜坡三维点云模型,主要分为以下4步:1)场地勘测。根据现场地形条件,选择无人机起降的位置,应尽可能平坦开阔。此外,须对斜坡大致走向进行判断并估计拍摄范围,为后续无人机航线设计提供重要参考。2)低分辨率三维地形采集。此步骤采用无人机倾斜摄影和地形跟随飞行技术。在地面控制系统输入无人机拍摄范围,设置飞行模式为地形跟随模式,输入数字高程数据(DEM),确定方位角,设置无人机飞行速度与图像重叠,无人机航向重叠率为80%,旁向重叠率为60%。完成以上操作后便可进行无人机倾斜摄影,并进行3D建模。3)多角度航线设计。根据研究区地形特征拟合出飞行平面,并结合现场调查所得结构面发育分组情况在飞行平面上规划无人机多角度拍摄航线,最后基于步骤2对建立的低分辨率三维模型进行检查并设计拍摄角度,为消除拍摄过程中的盲区需采用多角度进行拍摄。4)全景高分辨率图像采集。将上一步设计的多角度路线输入无人机当中,本研究采用大疆M300-RTK无人机进行作业,无人机质量为6.3 kg,最大飞行时间为55 min、最大可承受风速为15 m/s,RTK垂直精准度为1.5 cm+1×10-6×距基站基线距离(m),水平精准度为1 cm+1×10-6×距基站基线距离(m),如图2(a)所示。无人机所搭载禅思P1相机如图2(b)所示,质量约800 g、相机尺寸为198 mm×166 mm×129 mm、相机4 500万像素全画幅传感器面积为35.9 mm×24 mm、镜头焦距为35 mm、工作温度为-20～50 ℃。在进行无人机多角度贴近摄影之前,首先对相机进行检校,得到相机当前标定参数文件。在无人机摄影过程中,该参数会被自动写入,以此消除畸变对影像的影响。遥控无人机进入目标区域后,无人机自动执行所规划多角度拍摄航线,当无人机作业中遇到地形复杂坡面凹凸不平且存在视角盲区的区域,需操纵无人机进行多角度拍摄,如图3(a)所示。前视避障距离需设置为无人机拍摄距离之内,最后拍摄距离设置为<80 m,从而得到毫米级坡面影像。上述操作完成后便可将影像数据导入Context Capture软件中,对影像进行校正,进一步消除影像畸变,再经过图像特征匹配提取-空中三角测量-三维模型生成等步骤即可得到斜坡高精度三维实景模型,如图4所示。

2.2 结构面点云数据处理

由于通过上述步骤建立的是高精度研究区三维点云模型,还需人工识别面状结构面并进行结构面裁剪,提取毫米级结构面点云信息。其具体步骤:1)在Context Capture软件空间概要模块中,人为圈定研究区范围,选取坐标系为WGS84,生成该区域三维网络。在此基础上,设置输出点云密度为3 mm,坐标系与上一步保持一致,获取该区域带有图像色彩数据(RGB)信息的Las格式点云文件。2)将获取的点云文件导入Polyworks软件中人为识别并裁剪出面状结构面,提取结构面的形态信息。以结构面中心为原点建立三维坐标轴并将结构面二次裁剪为正方形,使点云数据规范化,如图5(b)所示,设置输出点云文件为TXT格式,以方便后期计算。3)将获取的不规则点云文件导入MATLAB软件中,使用Griddata函数对点云进行插值处理,求取点云规则化后(x,y)坐标所对应的结构面高程z,点云间距设置为Δx=Δy,利用Delaunay三角化原理对结构面进行三角剖分,实现结构面点云网格化,如图5(c)所示。

3 RS表征法简介与改进

3.1 RS表征法

RS表征法是EI-Soudani于1978年提出的采用RS表征值以表示物体面粗糙度的方法,弥补了传统方法用节理剖面线来表示整个结构面粗糙度等缺点,考虑了结构面的真实形态。其原理是将结构面视为由很多三角微元组成,所有三角微元面积总和表示结构面表面的实际面积,RS表征值即为结构面表面积与结构面的垂直投影面积之比,以此表示结构面的粗糙程度,RS表征值可表示为

RS=At/An

(1)

(2)

式中:At为结构面表面实际面积,An为结构面投影面积,Ai为结构面单元的实际面积,如图6所示。

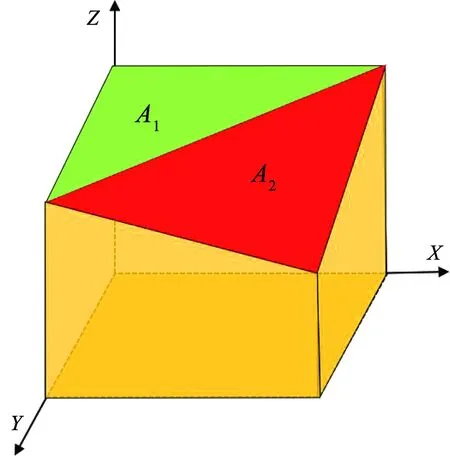
图6 RS表征法示意

3.2 RS表征法改进

使用原方法进行求解RS表征值时存在以下问题:当结构面产状不一致时,其结构面表面积可能存在差异,但却存在相同垂直投影面积,如图7所示,从而使得同一个垂直投影面积存在无数个不同产状结构面与之对应,导致所求RS表征值存在误差。

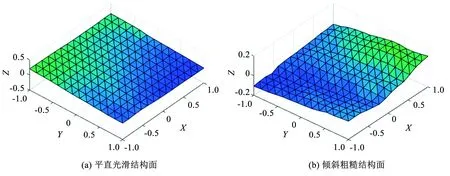
图7 不同结构面具有相同垂直投影面积

因此本文对原有方法进行改进,通过最小二乘法对结构面点云进行拟合得到唯一拟合平面,使用拟合后平面面积代替结构面垂直投影面积,如图8所示。

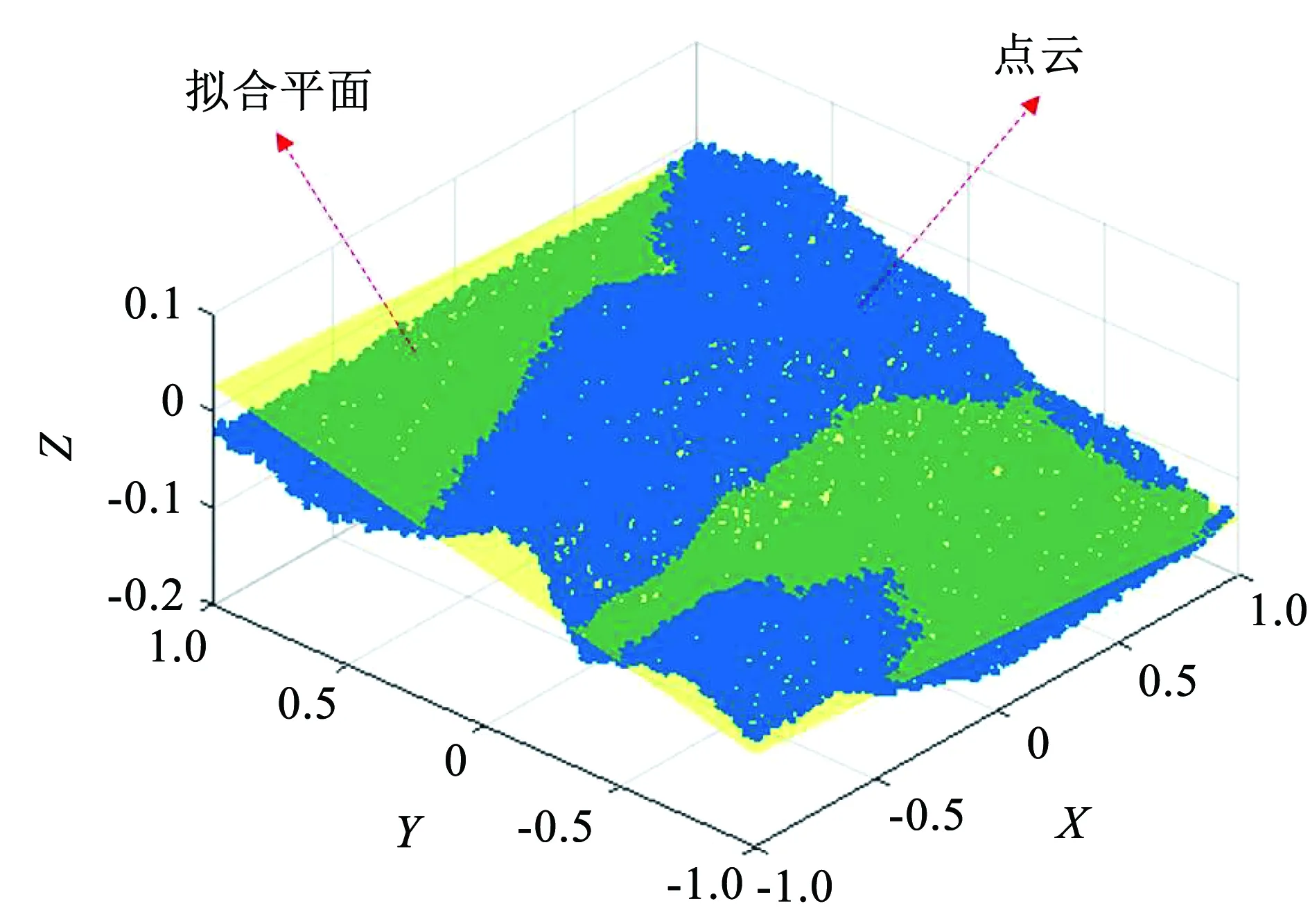
图8 结构面点云的拟合平面

建立拟合平面方程表达式

Ax+By+Cz+D=0,C≠0

(3)

将其转换为如下形式

(4)

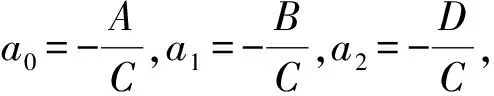
z=a0x+a1y+a2

(5)

构建最小二乘误差函数:

(6)

式中:(xi,yi,zi)为输入的三维点云坐标,i>3且不共线,当误差函数最小时,得到拟合平面。

视a,b,c为自变量,分别对方程(6)求导,可得

(7)

移项,整理可得

(8)

为方便求解,用矩阵形式表示上述方程组并转换形式得到a,b,c表达式为

(9)

将点云数据代入上式,即可求得a,b,c的值,得到拟合平面。

将(x1,y1),(xmax,y1),(x1,ymax),代入拟合平面方程中求出所对应的z1,z2,z3,利用公式

(10)

求得唯一拟合平面面积S,用此拟合平面面积代替其垂直投影面积。通过计算尺寸均为2 m的结构面RS表征值,采用垂直投影面积时得到RS表征值为1.010,采用最小二乘法拟合平面时得到RS表征值为1.074,两种情况所得结果相差较大。因此,通过此方法使得结构面与底面面积一一对应,解决了RS表征法在求解结构面粗糙度时的不确定性。

4 粗糙度定量分析

4.1 三角剖分对RS表征值的影响

在多个三角微元相互叠加求解结构面实际面积过程中,相邻4点存在两种三角剖分方式,如图9所示。不同剖分方式是否会对RS表征值产生影响,原方法没给有给出合理解释。鉴于此,本文分别在不同结构面尺寸、不同采样间距下对两种剖分方式的RS表征值进行计算,以探究剖分方式对RS表征值的影响。

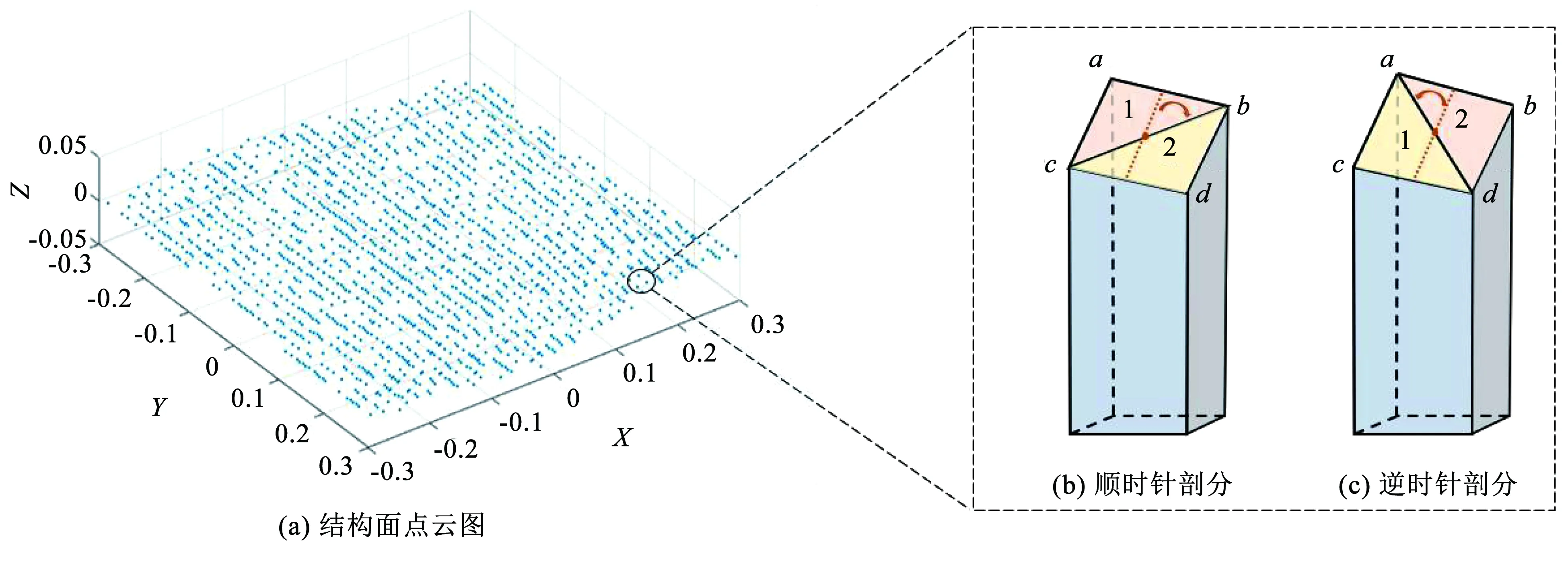
图9 不同的三角剖分方式

本文选取的结构面为5 m×5 m,研究不同采样间距下不同剖分方式对RS表征值的影响,结果见表1。结果显示:两种剖分方式得到的RS表征值差值随着采样间距增大呈减小趋势,且差值都在小数点后四位,最大差值率为0.61%,当采样间距等于0.01 m时,RS表征值差值<0.000 5,且最大差值率最小。因此在不同采样间距下剖分方式对RS表征值影响较小,仅当采样间距极小时会有所差异,其他情况下可以忽略两种剖分方式不同所引起的误差。

鉴于上述结论,本文将采样间距设置为0.01 m,结构面选取为2 m×2 m、2.5 m×2.5 m、3 m×3 m、3.5 m×3.5 m、4 m×4 m、5 m×5 m、5.5 m×5.5 m,研究在不同结构面尺寸下不同剖分方式对RS表征值的影响,结果见表2。结果显示:两种不同剖分方式所得RS表征值最大差值率均<1%。其中最大差值率为0.78%,最小值为0.17%。因此在不同结构面尺寸下剖分方式不会对RS表征值产生较大影响。

4.2 粗糙度尺寸效应

在探究结构面尺寸效应过程中,采用控制变量法,控制参数单一变化其他参数保持不变。结构面初始结构面尺寸设置为0.1 m×0.1 m,以固定步长0.1 m,正方形形心为中心向两边同时增加到最大采样尺寸,如图10所示,采样间距设置为0.01 m,其他参数保持不变,求取RS表征值。

图10 结构面采样尺寸范围划分图

为判别有效采样尺寸阈值,规定当在某一区间内,第i+1个表征值与第i个表征值差值<0.000 5时,便认定其存在有效采样区间。为直观判别有效采样区间,对上述阈值进行换算可得

Arc[(RSi+1-RSi)/D]<3.5°

(11)

式中:RSi表示某一尺寸结构面第i个RS表征值,RSi+1表示某一尺寸结构面第i+1个RS表征值,D表示采样步长。

如图11所示,对27条结构面的RS表征值研究发现,其粗糙度均存在尺寸效应:RS表征值随着结构面尺寸的变化而变化,最终趋于稳定。但变化规律与有效采样尺寸及其所对应的RS表征值存在差异,这是由于同一区域结构面的形成条件与类型不同所导致,拉张破坏形成的结构面表面相比于剪切破坏所形成结构面的表面更为粗糙,使得有效采样尺寸所对应的RS表征值较大。一些结构面(J6、J7、J14)整体上粗糙程度较为平均,起伏程度变化较缓,使得RS表征值相对稳定。而另一些结构面(J20、J23、J25)中心部分起伏度较陡,随着结构面尺寸的增大,起伏度逐渐变缓,导致RS表征值先增大后减小最后趋于稳定。还有与之起伏程度变化情况相反的结构面(J2、J3、J16),中心部分起伏度较缓,随着尺寸增大,起伏度逐渐变陡,致使RS表征值先增大最后趋于稳定。

图11 岩体结构面粗糙度评价结果随采样尺寸变化情况

在其中J2、J17等几个结构面中出现了一个结构面存在多个有效采样尺寸的现象,本文定义:同一个结构面中,把前几个出现的有效采样尺寸称为“假有效采样尺寸”,最后出现的有效采样尺寸称为“真有效采样尺寸”,以此来判别“真假有效采样尺寸”。出现此类现象的原因是:当采样尺寸较小时,任一结构面都可以找到起伏度变化相对平缓的区域;随着采样尺寸增大,会纳入一些凸起不平起伏较大的单元,导致RS表征值增大,随着采样尺寸的继续增大,当纳入凸起单元信息变化不大时,RS表征值重新趋于稳定,达到新的有效采样尺寸。此类现象多出现于大尺寸结构面中,在计算过程中要避免“假有效采样尺寸”的出现。

4.3 粗糙度间距效应

为研究结构面粗糙度的间距效应,保持采样尺寸,采样方向不变,只改变结构面采样间距。选取尺寸效应明显的7个典型结构面进行研究,如结构面J8、J10等。对结构面点云进行处理得到0.001 m的等间距点云数据并将采样间距设置如下:先从0.001 m以步长0.001 m增大到0.05 m,再从0.05 m以步长0.01 m增大到0.1 m,共设置55个采样间距。由于样本数较多,仅展示采样间距为0.03 m、0.05 m、0.1 m、0.2 m时的结构面三维网格模型,如图12所示。

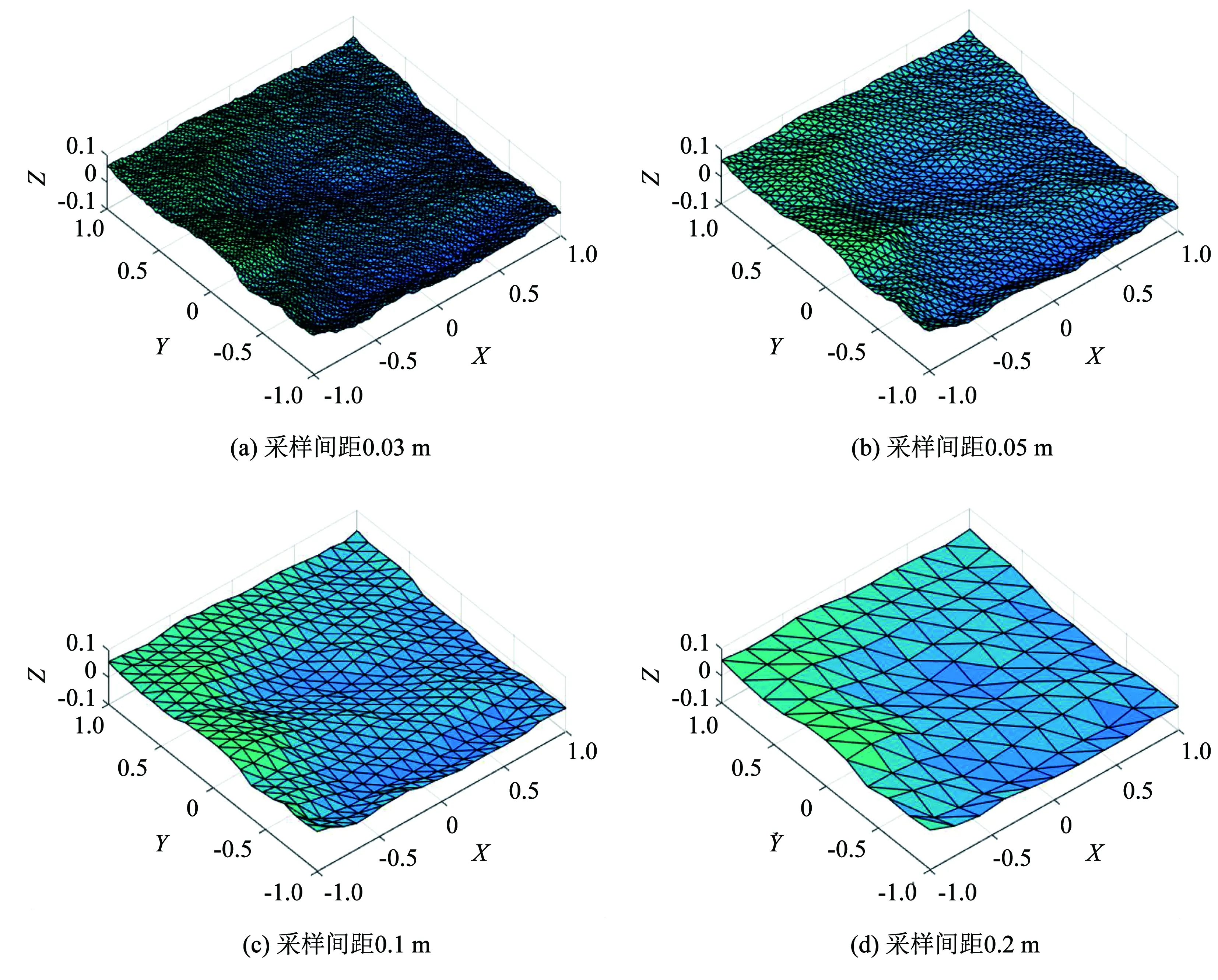
图12 不同采样间距下岩体结构面表面形态变化情况

使用改进后的RS表征法研究结构面粗糙度的间距效应,结果如图13所示。所有结构面RS表征值对采样间距十分敏感且变化趋势相近,当采样间距为0.001～0.002 m时,曲线斜率较小,RS表征值变化趋势较缓;当采样间距在0.002～0.02 m之间时,曲线变化十分明显,呈指数形式减小,RS表征值变化幅度在小数点后两位;当采样间距>0.02 m时,曲线斜率发生明显变化,变化趋势重新趋于平缓且RS表征值趋近于1,变化幅度在小数点后四位。结合不同采样间距下的结构面三维网格模型可以看出,当结构面采样间距越小时,点云分割精度更高,结构面形态越接近真实状况,更多细节被展示出来,结构面粗糙度越接近真实值。因此可以得出:当采样间距≤0.002 m时,RS表征值更能反映结构面真实粗糙程度;当采样间距>0.002 m时,RS表征值与结构面真实粗糙程度相差较大,不符合实际。确定采样间距为0.02 m为本文所研究的各尺寸结构面一阶大起伏、二阶小凸起的临界网格尺寸(采样间距),且该网格尺寸存在普适性。通过改进后的RS表征法对粗糙度间距效应进行分析,所得结果与实际观察结果相符,得出最符合结构面真实粗糙度的采样间距区间。此方法对采样间距敏感,因此较适用于求解高密度结构面点云数据下的结构面粗糙度表征值。

图13 岩体结构面粗糙度评价结果随采样间距变化情况

5 结 论

1)提出了一种无人机多角度贴近摄影测量技术,快速构建研究区高精度三维模型,从而获取毫米级结构面三维点云数据,解决了传统测量方法所建模型精度低等问题,为结构面粗糙度定量分析提供数据支撑。

2)提出了采用点云拟合平面代替垂直投影面积对RS表征法改进的新方法,并探究了不同三角剖分方式对RS表征值的影响。结果表明,改进RS表征法具有较高的准确性,同一采样尺寸与间距下,两种三角剖分方式对RS表征值的影响极小,可任选一种剖分方式求算RS表征值。

3)采用改进后RS表征法定量化研究岩体结构面粗糙度的尺寸效应与间距效应。所选取的27个结构面都表现出明显的尺寸效应,存在有效采样尺寸,部分结构面存在“假有效采样尺寸”与“真有效采样尺寸”,并提出“真有效采样尺寸”的确定方法。在进行间距效应研究时,改进后RS表征法对采样间距敏感,间距效应表现明显,得出采样间距≤0.002 m时,RS表征值更能反映结构面真实粗糙程度。此外,本文所研究结构面的一阶大起伏、二阶小凸起临界网格尺寸为0.02 m,且此网格尺寸存在普适性。