山区大跨度钢桁梁斜拉桥极限承载力分析

王泳金,任伟新,秦李冯

(深圳大学 土木与交通工程学院,广东 深圳 518061)

斜拉桥由主梁、桥塔和斜拉索组成,随着计算技术、施工工艺的不断进步,现代斜拉桥朝着跨度更大、桥塔更高、拉索更长的趋势发展。大跨度斜拉桥属于柔性超静定结构,结构组成复杂,整体结构的静力行为呈现明显的非线性,结构稳定问题突出。结构系统稳定性丧失有两种不同的临界状态:分枝点和极值点[1],对应两种完全不同的失稳问题。分枝点失稳问题,也称为第一类稳定问题,针对的是无任何初始缺陷的理想结构,结构一般处于弹性范围内,在数学上属于特征值问题,欧拉临界荷载就是一种最常见的分枝点失稳。

对于存在初始缺陷的实际结构,结构一旦承受荷载,就会产生相应的位移或变形,通过逐步加载直至结构破坏获取结构的荷载-位移曲线,曲线极值点所对应的荷载即为结构的极限承载力,称之为极值点失稳问题或第二类稳定问题,在数学上属于边界值问题。可以看出极值点失稳建立在非线性大位移理论基础上,反映结构整体极限承载能力,结构的极值点失稳极限荷载本质上就是结构的极限承载力。通过桥梁结构整体的极限承载力分析可以得到全桥整体的安全系数,可以清楚研究全桥最终的失效部位与失效路径[2-4]。

针对斜拉桥的极限承载力分析,国内外学者进行了大量的研究。文献[5]采用基于极值点失稳理论,研究了主跨605 m钢箱梁斜拉桥极限承载力,详细讨论了几何非线性、材料非线性以及双重非线性的影响,结果表明大跨度斜拉桥的极限承载力由斜拉索的材料非线性控制;文献[6]采用极值点失稳理论研究了主跨1 088 m苏通长江钢箱梁斜拉桥在不同施工阶段下的非线性稳定安全系数与失稳模态,分析加载过程中桥梁的极限状态;文献[7]研究了斜拉桥的极限行为,非线性分析中的增量迭代方法可以反映结构的变化如刚度改变、材料屈服或部分杆件的屈曲;文献[8]用非线性有限元方法研究了主跨为1 092 m沪通公铁两用长江大桥3种几何非线性行为,结果表明拉索的垂度效应对桥梁影响最大;文献[9]基于极值点失稳理论研究了主跨360 m叠合梁斜拉桥的非线性稳定的变化规律,得到了结构在加载至极限荷载过程中的失效路径及失效部位。

桥梁的设计一般基于弹性线性设计,随着跨度的增大,结构非线性效应越加明显,不同类型的斜拉桥表现出不同的非线性与极限承载力行为。针对本文云南山区主跨930 m的钢桁梁斜拉桥,该桥建成后将是世界第一大跨度山区斜拉桥,其非线性效应对结构的影响程度以及在极限荷载作用下全桥失效路径,亟需理解清楚,并分析钢桁梁构造特点对该类型桥梁极限承载力的影响。本文采用极值点失稳理论,考虑结构几何与材料双重非线性,进行稳定极限承载力分析,研究大桥在活载作用下的非线性行为和失效机制。鉴于山区风存在明显的“峡谷效应”,桥梁在施工中易受风荷载的影响,进行了最大悬臂施工状态的静风荷载的极限承载力分析,计算的结果可供同类桥梁设计与施工参考。

1 结构非线性分析

大跨度斜拉桥的极限承载力分析是研究桥梁结构逐级加载至整体失效的全过程,涉及结构的几何非线性和材料非线性,其中几何非线性包括索的垂度效应、梁与塔的压弯效应及大位移效应[10-12]。

材料非线性则取决结构各部分的材料性能。结构非线性有限元方程一般表示为

([K0]+[KL]+[Kσ]){δ}={P}

(1)

式中:[K]=[K0]+[KL]+[Kσ]为总刚度矩阵,[K0]为线弹性刚度矩阵,[KL]为大位移刚度矩阵,[Kσ]为初应力刚度矩阵,{δ}为节点位移列阵,{P}为节点荷载列阵。

结构非线性分析需要采用增量加载并选择参考构型,如果始终选取原始位置为参考构型,即采用整体的拉格朗日(TL)列式[13],则增量形式的有限元方程表示为

[KT]{Δδ}={ΔP}

(2)

式中:[KT]为单元切线刚度矩阵,{Δδ}为节点位移增量,{ΔP}为节点荷载增量。

采用增量法进行结构非线性时,在每一个增量步需要进行迭代求解,一般采用Newton-Raphson方法．结构的极限承载力对应着结构荷载-位移全过程曲线上的极值点,此时荷载-位移曲线斜率趋近于0,结构刚度趋于无穷大,为奇异点[14]。为了尽可能地得到该极值点所对应的荷载,也就是结构的极限承载力,在该极值点附件还需要采用弧长修正的方法,反复迭代。

采用增量法迭代求解结构非线性问题,每一个增量步有不平衡力收敛准则和不平衡位移收敛准则[15]。针对斜拉桥这类柔性结构体系,在非线性阶段会产生较大的位移,特别是针对极限承载力分析,要得到结构荷载-位移全过程曲线过极值点的下降段部分,一般采用位移收敛准则[16]。

斜拉桥各部位构件材料组成不同,主梁一般为结构钢,主塔为钢筋混凝土,拉索为高强钢绞线。斜拉桥材料非线性取决于组成各部分材料的非线性应力-应变关系。在进行极限承载力分析时,钢筋混凝土主塔由于变形较小,可以不考虑其材料非线性,按线弹性处理。拉索采用超高强度钢绞线,强度很高,其材料非线性按理想弹-塑性处理,不考虑屈服后的强化作用。主梁采用延性较好的结构钢,其材料非线性按考虑屈服后的强化来处理。

2 桥梁有限元模型建立与分析

以在建的云南山区大跨度钢桁梁斜拉桥为工程背景,大桥全长1 650 m,跨径分布(360+930+360)m,立面布置图如图1所示, 其中边跨拉索编号从桥台至主塔为B30～B1,中跨的拉索编号从主塔至跨中处为Z1～Z30。两主塔高度分别为330 m和385 m,桥面距山谷最深处460 m,该桥建成后将是世界第一大跨度山区斜拉桥。全桥共240根拉索,最长斜拉索长度接近500 m,边跨处各布置3组辅助墩。主跨主梁采用板桁结合钢桁梁,桁中心宽28.5 m,桁高8.5 m,边跨主梁采用钢桁-混凝土桥面板组合梁,主塔采用钻石型混凝土塔,辅助墩和过渡墩采用薄壁空心墩。

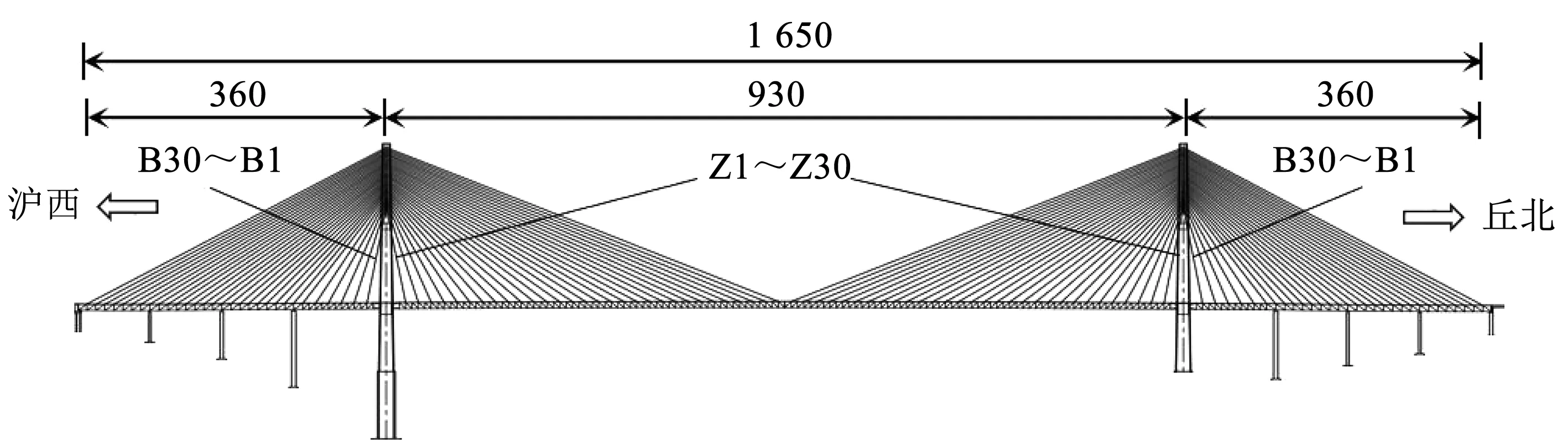
图1 全桥立面布置图(m)

结构极限承载力由结构加载直至失效全过程荷载-位移曲线得到,没解析解,目前普遍采用有限元数值求解[17]。大跨度斜拉桥结构复杂,需要采用不同单元模拟结构的不同部位。斜拉桥有限元模型采用梁单元模拟主梁全部桁架杆件及主塔;采用只拉不压的Link10杆单元模拟斜拉索,用施加单元初应变(应力刚化)的方式来考虑斜拉索的几何非线性;桥面板采用壳单元模拟以及墩台采用实体单元来模拟。主梁与桥塔的约束作用采用耦合单元来模拟,塔底和墩底采用固结的方式。建立的全桥有限元模型如图2所示,共计20 504个节点,15 480个单元。桥梁有限元模型各结构部位材料特性见表1。

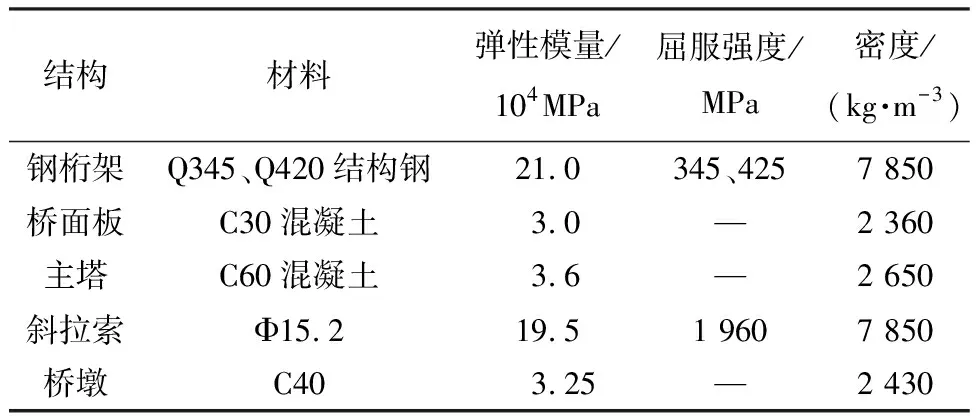
表1 结构材料特性

图2 全桥有限元模型

大跨度斜拉桥所受荷载以恒载为主,桥梁一旦合拢,在自重恒载作用下,结构构件内部存在很大的内力,全桥达到平衡,此时桥梁的平衡构型称为初始平衡构形。有限元模型主梁的初始平衡线形应尽可能地符合设计的线形,基于此,可以对所建立的有限元模型进行验证[17]。对于这一主跨930 m的斜拉桥有限元模型,在自重恒载作用下的有限元模型计算的线形与主梁设计线形的比较如图3所示,可以看出建立的有限元模型的主梁初始线形与设计线形吻合良好。

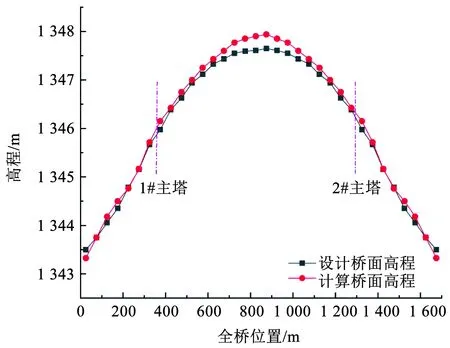
图3 主梁恒载计算线形与设计线形的比较

为确定桥梁的最不利活载荷载工况,图4给出了有限元计算的桥梁部分构件的内力、位移影响线。可以看出,当均布荷载满布于中跨,且集中荷载置于跨中时主梁挠度最大,此工况为主梁挠度最不利活载荷载工况。

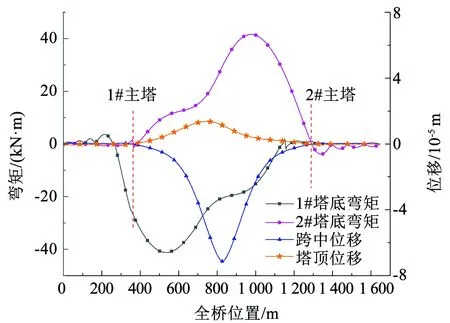
图4 位移、内力影响线

3 极限承载力分析

在几何非线性分析中,利用Link10单元的应力刚化来考虑索的垂度效应,主梁、主塔采用大位移、大转动和小应变梁单元,并打开大变形开关(NLGEOM,ON)以考虑结构的几何非线性;在材料非线性分析中,采用BKIN模型考虑钢材的塑性及Von Mises屈服准则。

进行桥梁极限承载力分析时,取自重恒载+中跨满布汽车活载工况作为后续的分析工况。采用逐级加载的方式进行极限承载力分析,将考虑车道折减的活载qk、Pk作为基准荷载。引入活载系数λ,则极限承载力计算施加的荷载为

P=λ(qk+Pk)

(3)

3.1 几何非线性分析

假定材料为线弹性,在初始平衡构形基础上研究活载作用下几何非线性对结构性能的影响如图5所示。图5(a)、5(b)分别为随着活载的增加主梁跨中、主塔塔顶的荷载-位移曲线,同时给出了线弹性结果进行比较,可以看出:1)当活载加载系数λ较小时,也就是活载较小时,几何非线性与线弹性分析计算曲线基本重合,表明在荷载较小时,几何非线性对结构行为影响较小;2)当活载加载系数λ大于20左右,几何非线性对结构行为产生明显的影响,这种影响随着荷载的增大而增加;需要说明的是活载加载系数λ大于20,已经远远大于设计荷载,也就是说在正常使用荷载作用下,几何非线性对结构行为影响较小。

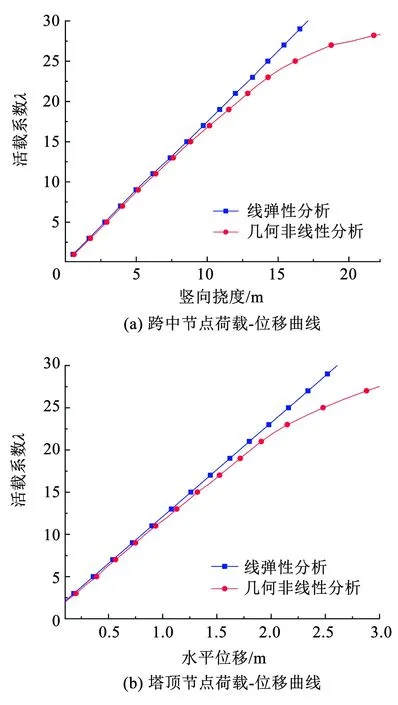
图5 几何非线性对结构的影响

3.2 几何与材料双重非线性分析

在上述的结构线性和几何非线性分析过程中,桥梁活载已经施加得足够大,结构的变形达到了非常大的量级,事实上由于结构构件材料强度的限制,实际桥梁的变形不可能达到如此之大。因此,桥梁结构的极限承载力分析必须考虑材料非线性。

斜拉桥一般由钢筋混凝土主塔、超高强度拉索和结构钢主梁组成。为了研究每一部分不同材料非线性的影响,进行双重非线性分析时材料非线性分别研究:1)斜拉索材料非线性,主塔和主梁为线弹性;2)钢主梁材料非线性,主塔和斜拉索为线弹性;3)钢主梁和斜拉索材料非线性,主塔为线弹性。4种非线性计算工况得到的主梁跨中荷载-位移曲线如图6所示,计算时主梁和斜拉索材料非线性模型为理想弹塑性模型,桥梁极限承载力结果表明:1)在加载前期,即活载较小时,4条曲线基本重合,说明几何、材料非线性对全桥影响较小;2)对比曲线2、3的极值点,看出结构在考虑索的材料非线性后极限承载力明显降低,表明索是极限承载力大小主要控制因素,是斜拉桥的主要承力构件;3)对同时考虑斜拉索与主梁材料非线性进行分析(曲线4),中跨处的Z24斜拉索率先开始屈服,应力达到1 960 MPa后发生断裂,紧接着Z25也开始屈服,斜拉索屈服顺序由中跨Z24开始向两侧延伸,此时对应位置的主梁杆件已受拉屈服。随着外荷载的增加,个别斜拉索失效,并非意味着整个桥梁极限承载力的丧失,随着主梁挠度不断增大,主梁部分区域材料进入屈服,最终全桥失去承载能力。

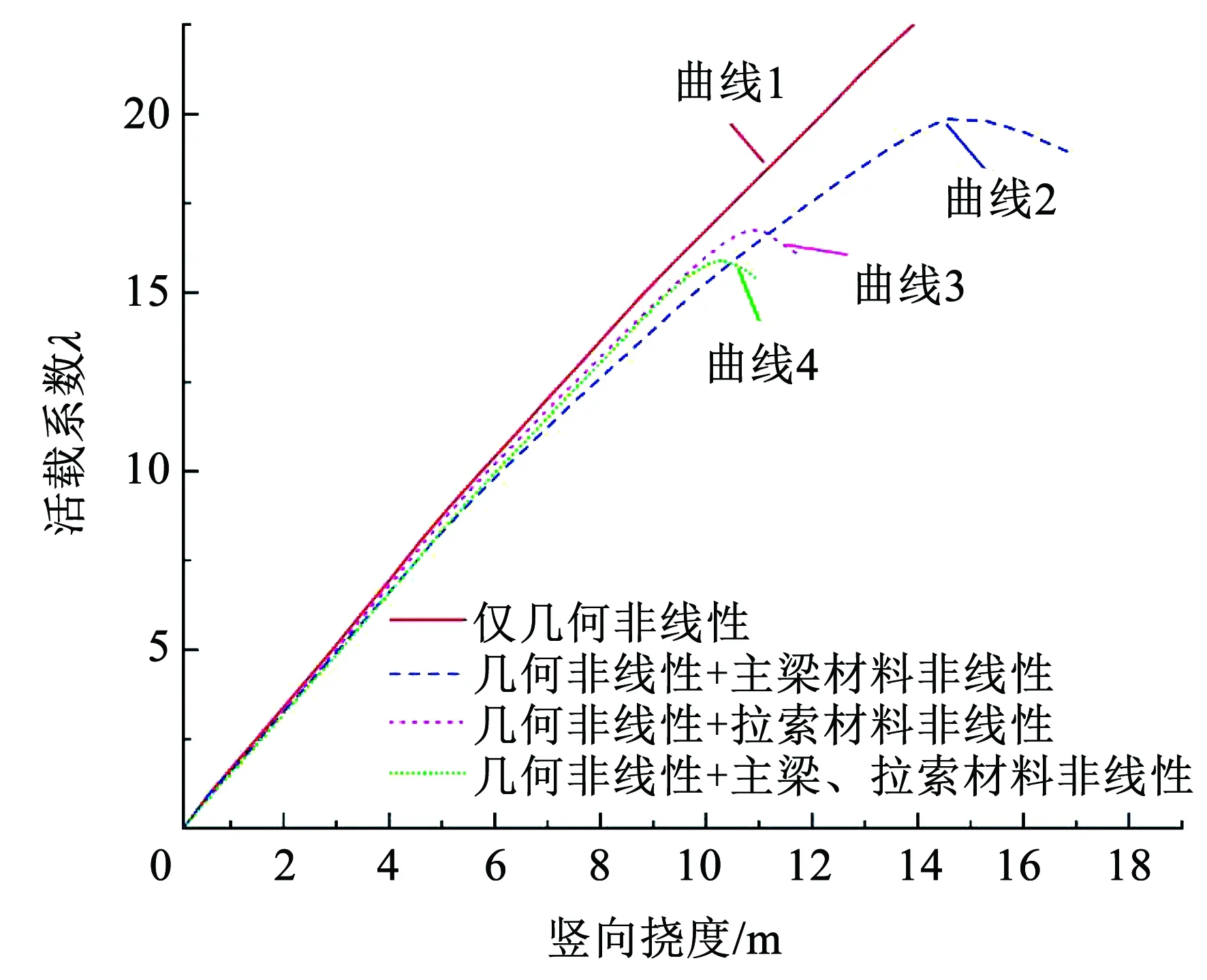
图6 主梁跨中的荷载-位移曲线

为进一步获得全桥失稳时的临界荷载,在考虑几何非线性和主梁、拉索材料非线性情况下,选取主塔、主梁部分控制点进行结构稳定分析,并画出各控制点荷载-位移曲线如图7所示,由图7可看出,当λ=16.3时,主梁、主塔上的控制点变形急剧变化,可知全桥已发生失稳破坏,此时主塔水平位移为1.8 m,主梁跨中挠度为10.2 m。

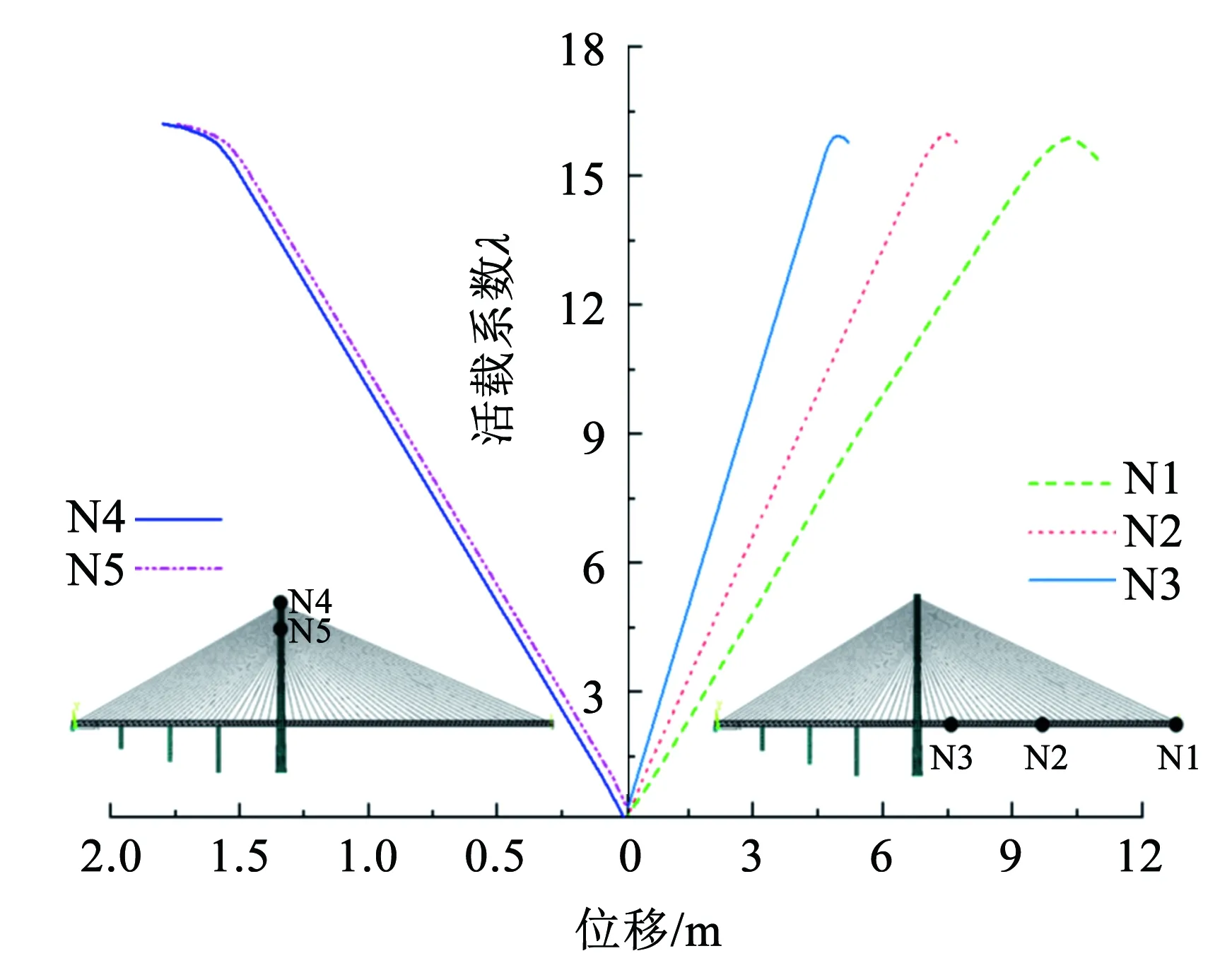
图7 控制点荷载-位移曲线

同时考虑斜拉索与主梁材料非线性时主梁失效机制与路径如图8所示,可以看出,随着活载系数λ的增大,即外活载的增加,主梁弹塑性区逐渐发展,钢桁梁主梁各杆件先后出现了4条失效路径,分别是两条受拉失效路径和两条受拉失效路径,受拉失效路径从跨中和边跨桥台侧向主塔方向延伸,受压失效路径是从主塔两侧向跨中、边跨桥台侧延伸。

4 最大悬臂施工状态横向极限承载力分析

针对本文研究的山区超大跨径斜拉桥,由于风“峡谷效应”的存在,山区深谷地区的风速较平原地区的大[19]。斜拉桥在最大悬臂施工阶段时结构轻柔、整体刚度较低,受风荷载的影响较大,是施工过程中最危险的阶段,故有必要对此阶段进行极限承载力分析,了解最大单悬臂施工状态下能承受的最大横向静风荷载。

根据《公路桥梁抗风设计规范》[20],桥梁顺风向等效静阵风荷载计算公式为

(4)

式中:ρ为空气密度,Ug为等效静阵风风速,CH为主梁横向力系数,B为主梁的特征宽度。

取斜拉桥最大悬臂施工状态作为分析对象,采用对主梁施加横向均布荷载的方式来模拟横向静风荷载对结构的作用,按比例增加式(4)给出的等效静风荷载,考虑几何与材料的双重非线性,进行横向极限承载力分析,计算得到的斜拉桥在最大悬臂施工阶段最大悬臂处横向荷载-位移曲线如图9所示。同时,将不同风速对应的风等级换算成横向荷载也标识在图9中,计算结果表明:1)大跨度斜拉桥最大悬臂施工状态时,结构在横向荷载的作用下,主梁在最大悬臂端处横向位移随着荷载的增大呈较明显的非线性趋势;2)最大悬臂施工状态横向极限承载力远大于十二级风对应的静风荷载。

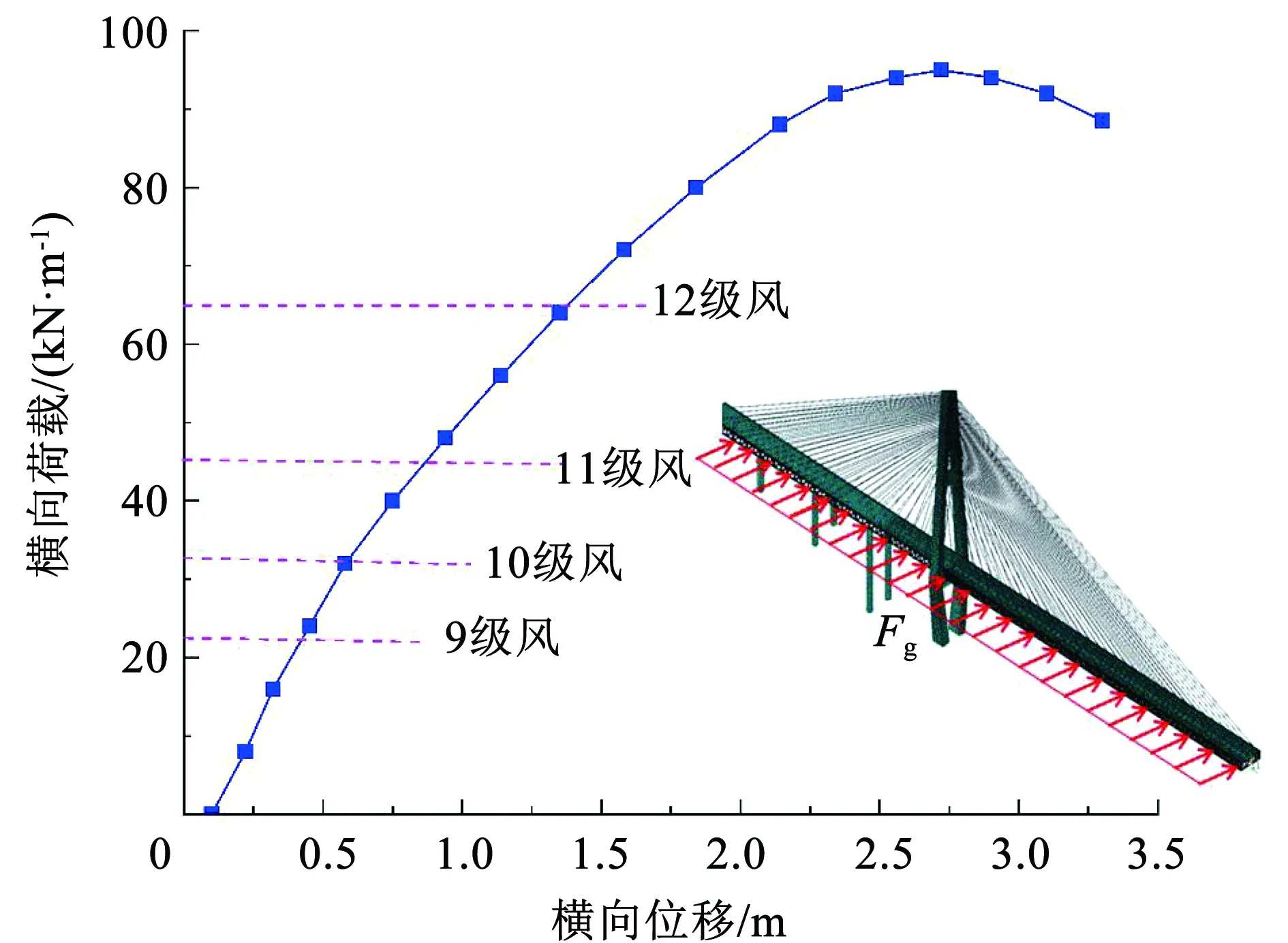
图9 最大悬臂施工状态横向荷载-位移曲线

5 结 论

本文以云南山区主跨930 m的大跨度钢桁梁斜拉桥为背景,采用极值点失稳理论,考虑结构几何与材料双重非线性,进行成桥面内和最大悬臂施工阶段横向稳定极限承载力分析,探讨了大桥的非线性行为和失效机制,结论如下:

1)在正常设计荷载作用下,几何非线性效应对桥梁结构的静力性能影响很小;斜拉桥的极限承载力由拉索的材料破坏控制,材料非线性是极限承载力的主要控制因素。

2)随着荷载的增加,个别拉索在达到其材料强度后而失效,主梁的挠度呈非线性增加,导致主梁的应力最大部位发生屈服;主梁各杆件先后出现4条失效路径,两条受拉失效路径从跨中和边跨桥台侧向主塔方向延伸,两条受压失效路径是从主塔两侧向跨中、边跨桥台侧延伸;随着主梁屈服区的扩展,全桥达到了极限承载力,此时桥塔仍处于弹性状态。

3)大跨度斜拉桥在最大悬臂施工状态整体刚度较低,在横向荷载作用下表现出较明显的非线性特性;最大悬臂施工状态横向极限承载力远大于十二级风对应的静风荷载。