非充分激励条件下路面附着系数估计算法
赵永坡,孙晖云,李 斌,李 飞,景立新,张 琳
(1.长城汽车股份有限公司,河北 保定 071000;2.同济大学 电子与信息工程学院,上海 201804;3.同济大学 汽车学院,上海 201804)
0 引言
路面附着系数对于提高车辆控制系统性能至关重要。经现有事故调查发现路面附着系数与事故发生率有关,路面附着系数越低事故发生率越高[1]。路面附着系数是计算轮胎力的关键参数之一,极大地影响了车辆底盘控制系统、辅助驾驶系统(advanced driver assistance systems,ADAS)和防抱死制动系统(antilock brake system,ABS)等控制效果[2-4]。因此,实时估计路面附着系数成为了保证车辆稳定性和安全性的关键。
现有常用的路面附着系数估计算法分为2类,分别为基于特殊传感器(声学、光学、应变片)的估计方法和基于车辆动力学模型的卡尔曼估计方法。其中基于特殊传感器估计方法在声学方面通常利用轮胎在不同路面上噪声差异判断路面类型,在光学方面通常利用摄像头捕捉实时路面照片信息进行识别,在应变片方面通常使用内嵌轮胎内部的应变片识别轮胎在不同路面上的变形量的差异。但是,在现实交通环境中变化的环境光、不平的路面、环境噪声等不确定性干扰导致上述方法存在抗干扰能力弱、输出估计分辨率低的问题[5],而基于车辆动力学模型的卡尔曼估计方法识别精度较高且采样频率较快。因此目前基于车辆动力学模型的估计方法作为一种主流的估计方法,在车辆控制系统中得到了广泛应用。
现实交通场景中驾驶员决定了车辆的运行状态,如加速、减速、换道等。现实工况的不同行为直接对应于估计算法的激励程度不同。以纯侧滑工况为例说明激励程度含义,如图1所示,A区域轮胎力处于线性段,同一轮胎侧偏角在不同路面附着系数的路面上所产生的轮胎力相差较小,这种小激励条件下估计算法的识别精度较低。由于B区域轮胎力处于非线性段,同一轮胎侧偏角在不同路面附着系数的路面上所产生的轮胎力相差较大,这种大激励条件下估计算法能够快速收敛到路面附着系数的真实值[6]。现实车辆运行工况中车辆的激励程度是随机的,完全由驾驶员的意图所决定。随机的激励程度导致估计算法的估计精度下降。目前多使用卡尔曼滤波器作为路面附着系数估计的主要方法,当激励程度较小时,若不能及时准确地对协方差参数进行修正,较小的激励条件将会导致估计算法精度降低甚至失效。同时,由于路面条件的突变是未知的,此时利用未考虑状态量扰动的标准卡尔曼滤波器算法的收敛速度慢,无法快速地跟随上路面附着系数的突变导致路面估计精度下降而不可使用[7]。
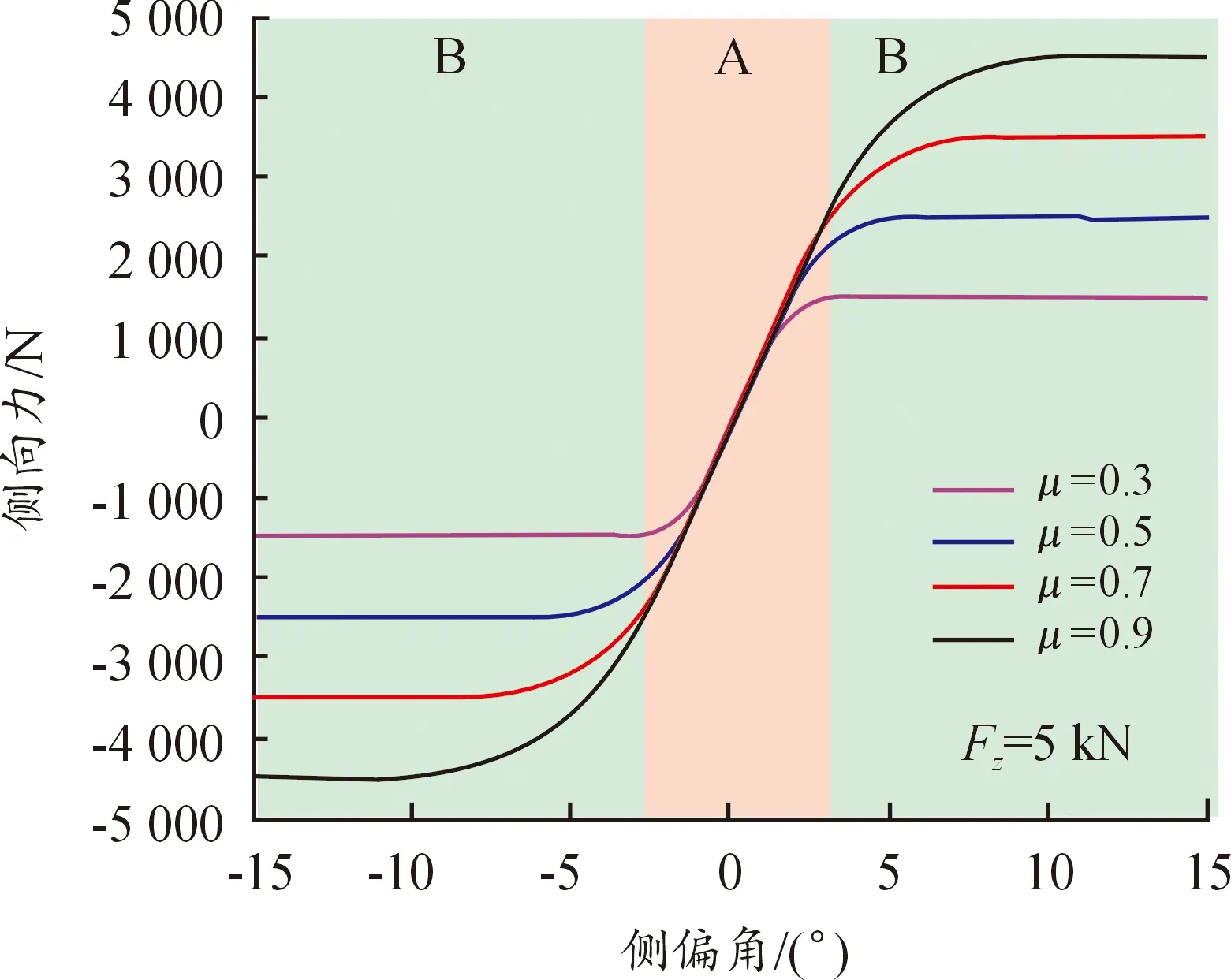
图1 纯侧滑下不同路面轮胎侧向力
国内外学者为解决上述问题进行了大量研究,有些学者针对不同工况的不同激励程度设计路面附着系数估计算法。为了适应不同激励条件,Ahn等[6]提出了一种不同激励条件算法融合方案,分别基于不同激励条件下的特性设计对应的估计算法,再根据激励程度进行切换保证不同激励条件下的精度。但是,算法切换条件的设定和平滑程度决定了估计算法的精度。针对该问题,熊璐等[8]提出了一种模糊自适应路面附着系数融合估计方法,利用模糊推理系统估计车辆的激励条件,实时调整路面附着系数估计算法,提高了算法对不同工况的估计适应能力。李刚等[9-10]提出了一种基于双容积卡尔曼滤波的联合估计方案,提高了估计算法对不同行驶状态的适应性。为了提高估计算法对路面条件不确定性的鲁棒性,一些学者使用了改进的Sage-Husa自适应滤波算法实时对系统方差和量测方法进行调整,提高了算法估计精度[11-12]。但基于次优的Sage-Husa算法导致估计算法对突变工况的收敛速度不足[13]。还有些学者使用强跟踪因子对卡尔曼滤波进行修正,保证在系统发生突变时及时调整系统方差,提高卡尔曼滤波的收敛速度[14]。Wang等[15]设计了一种基于强跟踪无迹卡尔曼滤波的路面附着系数估计器,提高了算法在路面突变时的收敛速度。但这类方法在调整系统方差时未考虑当前工况的激励条件,若在小激励条件下调整系统方差将导致算法估计精度降低甚至失效。
为了提高多种工况下路面附着系数估计算法的性能,本文在上述研究的基础上设计了一种基于模糊工况自适应强跟踪卡尔曼滤波的路面附着系数估计算法,估计方法选用强跟踪卡尔曼滤波,其中强跟踪因子能够及时调整系统方差,提高估计算法的鲁棒性。同时将强跟踪因子、车辆状态估计信息和传感器信息作为模糊推理系统的输入,模糊推理输出修正后的强跟踪因子,显著降低了小激励条件下估计值的波动幅值。采用控制器硬件在环试验台的方式对所提算法的估计效果进行了验证,结果表明:算法在保持了对突变工况的跟踪能力的同时,适应了不同工况的激励程度,显著降低了估计值的波动幅值。
1 整车动力学模型
1.1 3自由度车辆动力学模型
为了保证路面附着系数估计算法能够在多种工况下进行估计,本文建立了表征车辆纵向、横向和横摆等3个方向的动力学模型,如图2所示。基于以下假设:忽略车身与车轮间相互作用力;左前轮和右前轮等效为前轴,左后轮和右后轮等效为后轴;左右前轮转角相同;车辆是对称的等假设简化车辆模型的复杂度,提高估计算法的计算效率。
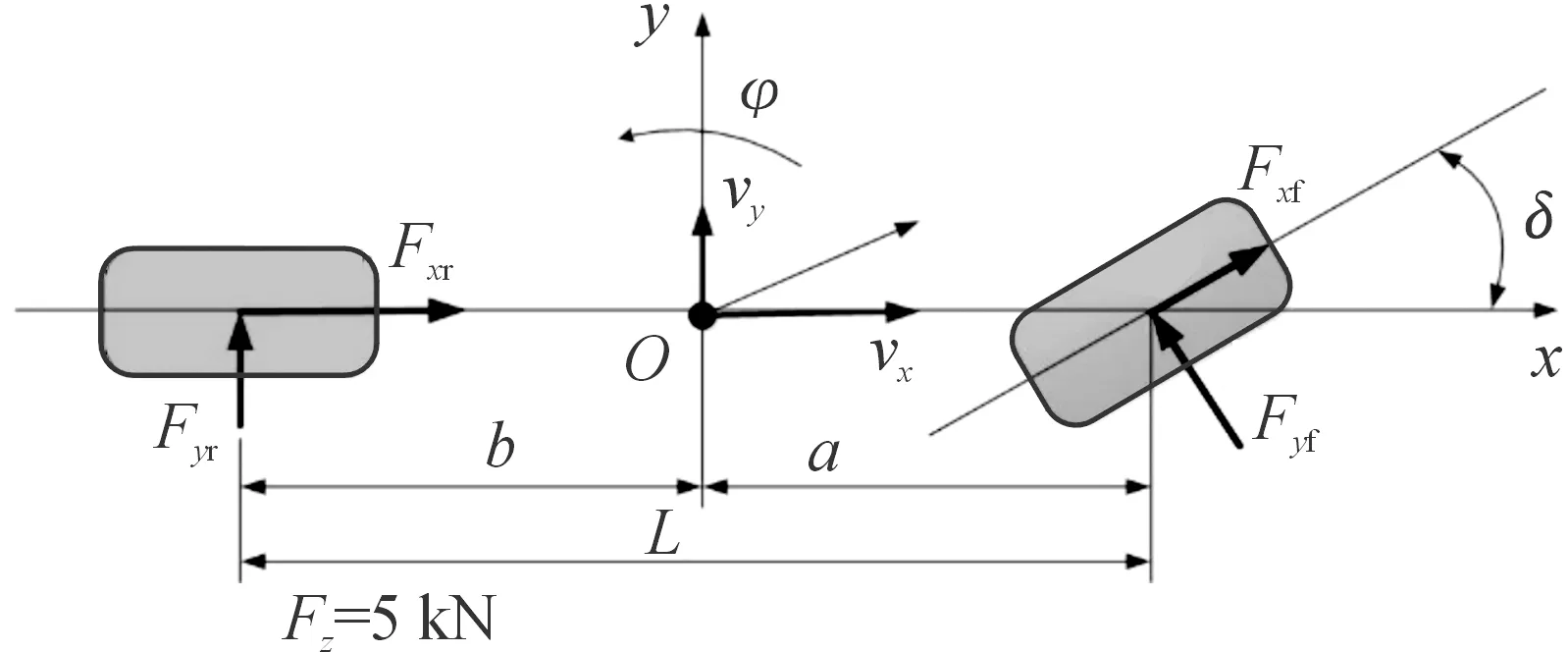
图2 3自由度车辆动力学模型
车辆纵向动力方程,图2中x轴方向:
(1)
车辆侧向动力方程,图2中y轴方向:
(2)
车辆绕z轴的横摆动力学方程
(3)
式中:m为汽车质量,kg;Fxf、Fxr分别为车辆前轴纵向力和后轴纵向力,N;Fyf、Fyr分别为车辆前轴侧向力和后轴侧向力,N;ax、ay分别为车辆纵向加速度和侧向加速度,m/s2;φ为车辆横摆角速度,rad/s;Iz为车辆的绕Z轴的转动惯量,kg·m2;La、Lb分别为质心到前轴距离和质心到后轴距离,m;δ为车辆的前轮转角,rad;Mz为车辆的横摆力矩,N·m。
1.2 修正的Burckhardt轮胎模型
如1.1节所示的车辆动力学模型,其中前后轴的纵侧向力是决定车辆运动状态的关键。考虑到估计算法在车辆纵横向工况下性能,本文采用了Burckhardt复合轮胎模型。该模型需要的参数较少,且路面附着系数的影响便于提取出来。
车辆前后轴纵侧向滑移率计算公式:
(4)
(5)
式中:sxi为前后轴的滑移率,i={f,r};rdyn为轮胎有效半径,假设左右轮胎有效半径相等,m;wwi为前后轴的轮速,rad/s;syf为前轴侧向滑移率;syr为后轴侧向滑移率。考虑到摩擦力椭圆的影响,计算复合滑移率时在纵向滑移率上加上了待标定的比例系数ks。
(6)
式中,si为车辆前轴综合滑移率。接下来给出修正的Burckhardt复合轮胎模型,由于大多数常规工况下,滑移率较小,因此忽略在轮胎力饱和阶段轮胎力的下降。该模型的公式如下所示:
f(si)=μc1(1-e-c2si)
(7)
(8)
式中:f(si)为名义轮胎力;syf为前轴侧向滑移率;syr为后轴侧向滑移率;Fzi为车辆前后的垂向载荷;c1、c2为轮胎模型中参数,该参数由轮胎特性所决定;μ为路面附着系数,由车辆行驶环境决定。
车辆前后垂直载荷公式:
(9)
式中:L为车辆前后轴之间的距离,m;g为重力加速度,m/s2;h为质心距离地面高度,m。
2 模糊工况自适应强跟踪卡尔曼滤波
2.1 路面附着系数估计算法架构分析
本文提出的基于模糊工况自适应强跟踪卡尔曼滤波的路面附着系数估计算法的流程如图3所示。通过硬件在环试验台采集车辆状态变量包含:四轮轮速、车辆纵侧向车速、前轮转角、纵侧向加速度和横摆角速度等;根据在第1章中建立的车辆动力学模型和轮胎模型计算得到前后轴的纵侧向力估计值和纵侧向加速度估计值;根据量测信号和估计值计算得到强跟踪因子输入给卡尔曼滤波算法;基于模糊推理系统模糊化车辆状态信号输出修正后强跟踪因子;基于改进后的卡尔曼滤波器估计路面附着系数。强跟踪因子和模糊推理系统的引入平衡了收敛速度和估计值稳定性之间的矛盾,显著提高了在路面条件发生突变时的估计算法收敛速度。
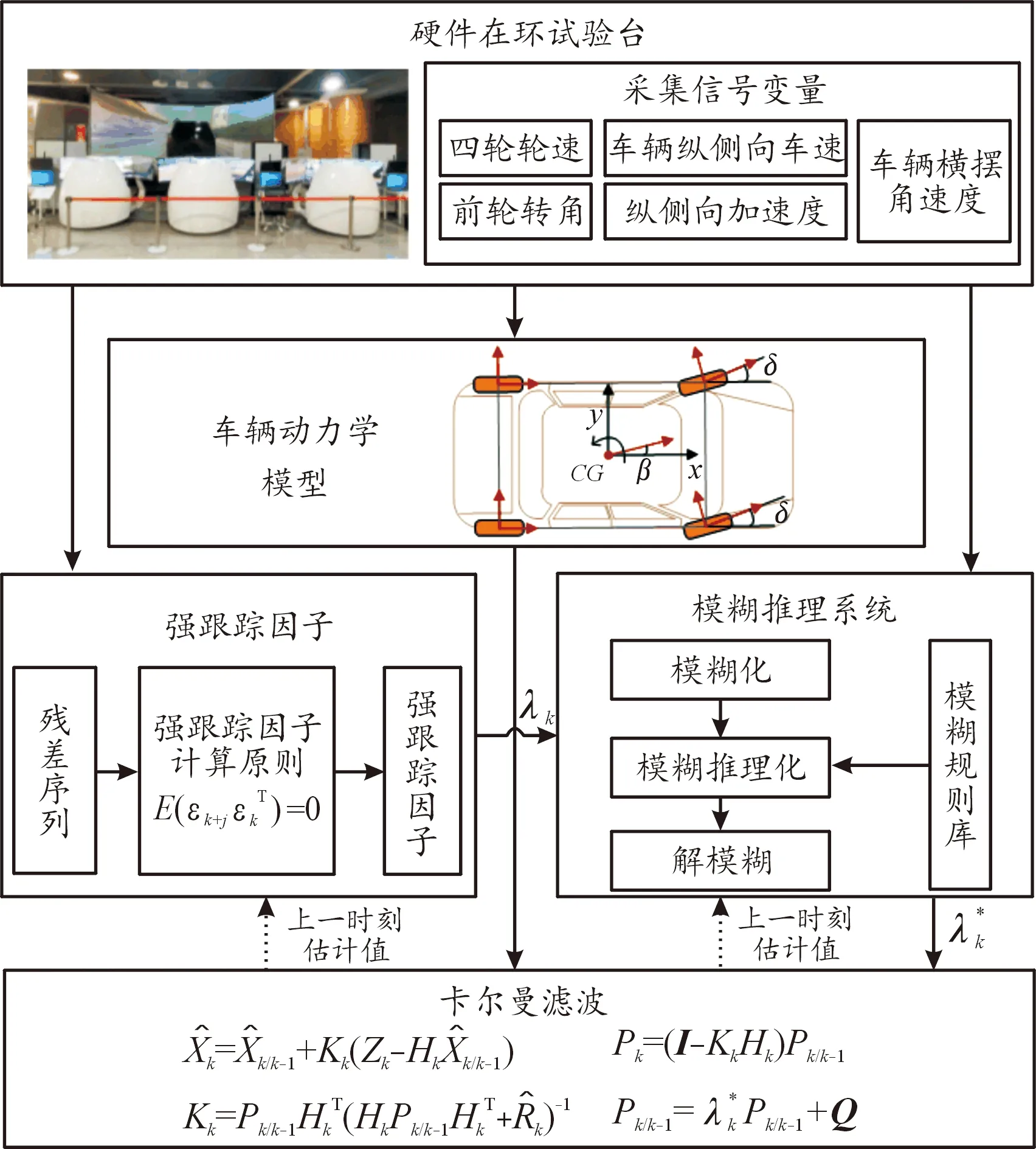
图3 路面附着系数估计算法流程框图
2.2 强跟踪卡尔曼滤波器设计
为了增强估计算法的鲁棒性,引入强跟踪因子对卡尔曼滤波中的状态预测方差进行实时调整,构造了基于强跟踪卡尔曼滤波器的路面附着系数估计方法。根据第1章中的车辆动力学模型构造卡尔曼滤波的状态方程和观测方程:
(10)
式中:Xk为系统的状态序列,表示路面附着系数;Zk为系统的观测序列,包含纵向加速度、侧向加速度和横摆角速度;Vk为系统的观测噪声;Hk为观测矩阵,矩阵中的h1、h2、h3可以由车辆动力学模型得到;关于系统的观测噪声的统计特性,进行假设如下所示:
(11)
式中:Rk为观测噪声Vk的对称正定方差矩阵;δkj为Kronecker-δ函数。
2.2.1标准卡尔曼滤波
标准算法的公式如下所示。
状态一步预测及其预测误差方差为:
(12)
滤波增益矩阵为:
(13)
更新估计误差方差为:
(14)
路面附着系数估计值为:
(15)
2.2.2强跟踪因子设计
由于路面条件的不确定可能导致路面附着系数发生突变,使得系统模型存在大量的不确定性,此时标准卡尔曼滤波中的估计误差方差将与实际系统不匹配。
因此,为了提高路面附着系数估计算法的鲁棒性,引入强跟踪因子,利用衰减记忆滤波的方案,将渐消因子引入估计误差方差中,从而降低旧数据对于卡尔曼滤波器的影响,更加关注于新数据对于估计算法的影响,使得强跟踪卡尔曼滤波器能够较好地跟踪路面条件突变所引起的路面附着系数变动。在标准卡尔曼滤波算法基础上计算强跟踪因子,并在计算状态预测方程Pk,k-1时与之相乘便是强跟踪卡尔曼滤波算法:
Pk,k-1=λk-1Pk-1
(16)
式中:λk≥1为自适应渐消因子,参考文献[14]计算方法:

(17)
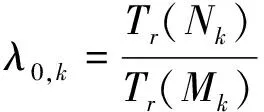
(18)
Nk=Vk-lRk
(19)
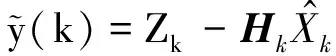
(20)
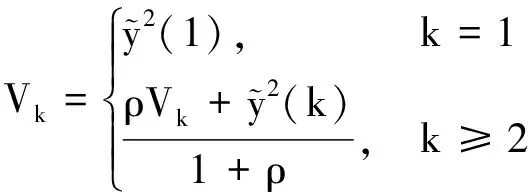
(21)
(22)
式中:0<ρ≤1为遗忘因子;l≥1为遗忘因子,取值根据实际试验具体调整。
2.3 模糊工况自适应系统设计
2.3.1模糊推理系统设计原则
设计基于模糊方法的工况激励条件自适应策略,通过车辆状态估计值和传感器测量值模糊推理出当前车辆运行工况的激励程度,而后根据2.2.2小节中提出的强跟踪因子,设计不同激励程度下对强跟踪因子的修正方法,保证估计算法在较大激励条件下强跟踪上路面附着系数的突变,并在小激励条件下降低路面附着系数估计值的波动幅值。
模糊推理系统共有强跟踪因子和工况激励因子2个输入,输出为修正后的强跟踪因子。其中工况激励因子根据下述公式计算求得:
(23)
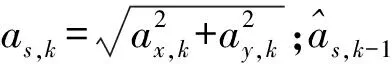
2.3.2输入模糊化
考虑到计算复杂和模糊化效果的鲁棒性,本文利用三角隶属度函数法设计模糊化函数。模糊化后的隶属度可以通过以下等式来计算:
(24)
式中:a、b、c分别为三角形隶属度函数的左底边、右底边和顶点在横轴上的坐标。图4为3种不同情况下的隶属度函数曲线。
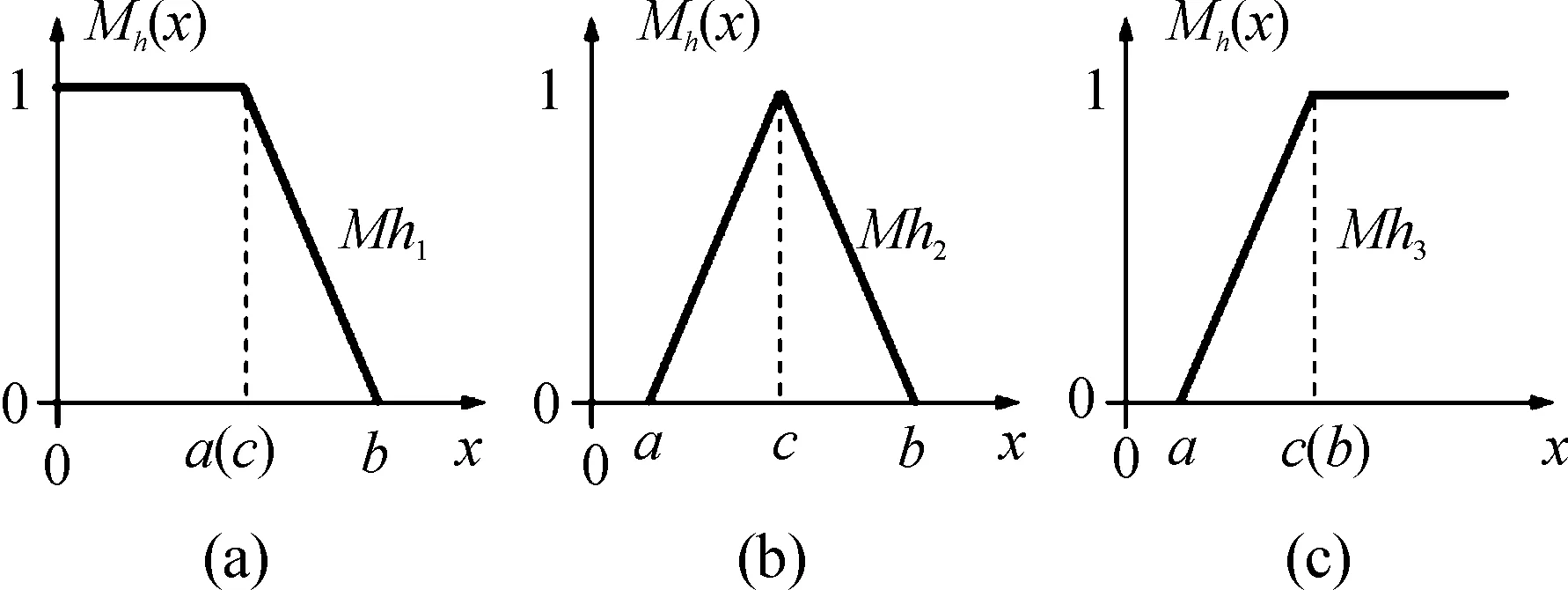
图4 三角隶属度函数的3种曲线
图5为强跟踪因子输入的模糊化隶属度函数曲线,强跟踪因子的取值范围为λk∈[1,∞),本文将强跟踪因子模糊化成为4个不同的跟踪强度的三角隶属度函数,其中γ2、γ3、γ4分别为较弱、较强和强3个函数的顶点对应的横坐标,为系统待标定参数。图6为工况激励因子输入的模糊化隶属度函数曲线,根据工况激励因子的定义可以得到其取值范围为,本文将工况激励因子模糊化为4个不同的跟踪强度的三角隶属度函数,其中分别为较小、较大和大这3个函数的顶点对应的横坐标,为系统待标定参数。
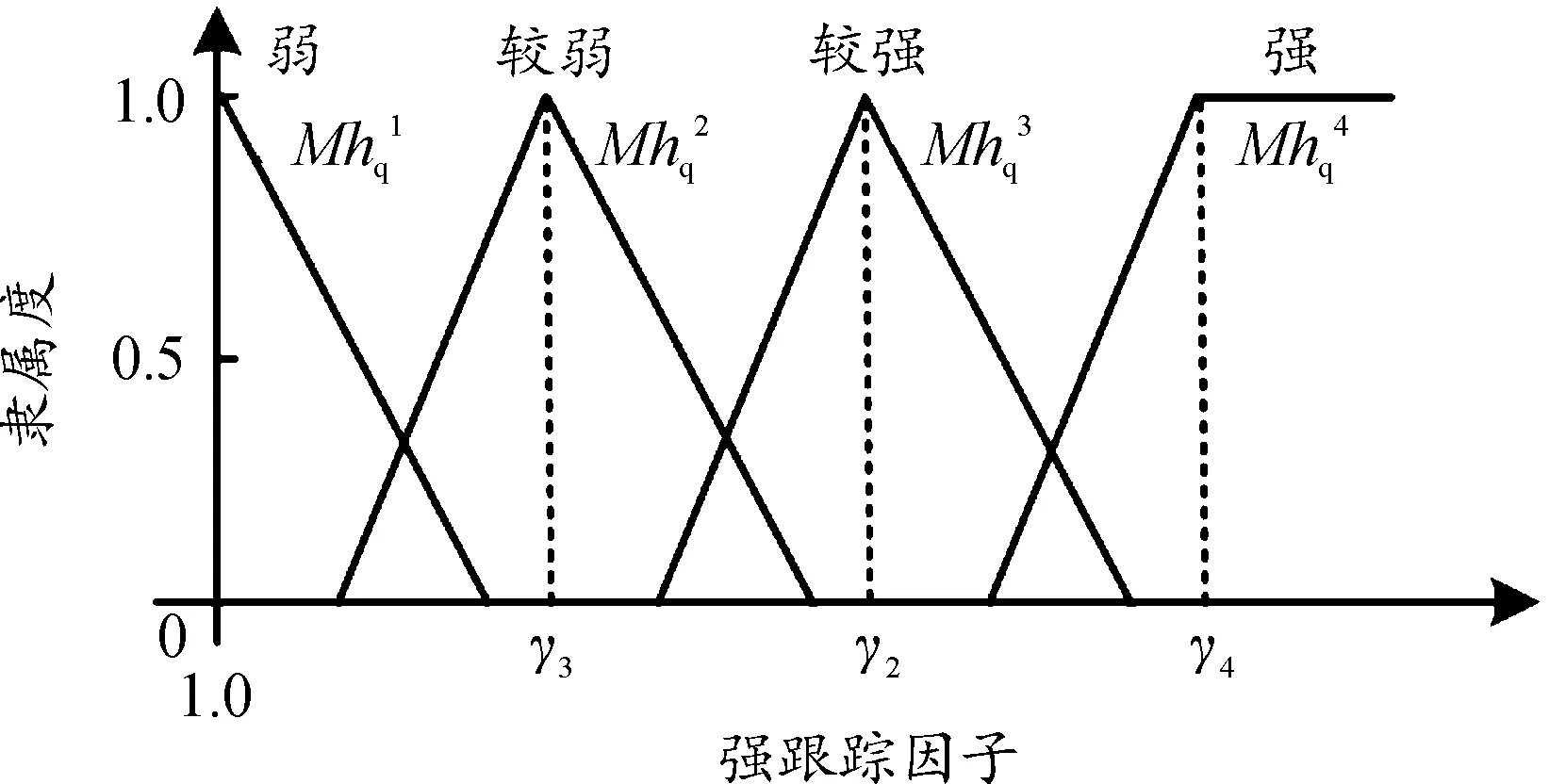
图5 强跟踪因子的模糊化隶属度函数曲线

图6 工况激励因子的模糊化隶属度函数曲线
2.3.3模糊推理规则及去模糊化
根据实际工况制定如表1所示的模糊推理规则。根据表1建立工况激励因子、强跟踪因子与补偿增益之间的映射关系。

表1 模糊推理规则
图7为输出解模糊隶属度函数,ti为不同补偿增益Ti对应的横坐标,为系统待标定参数。
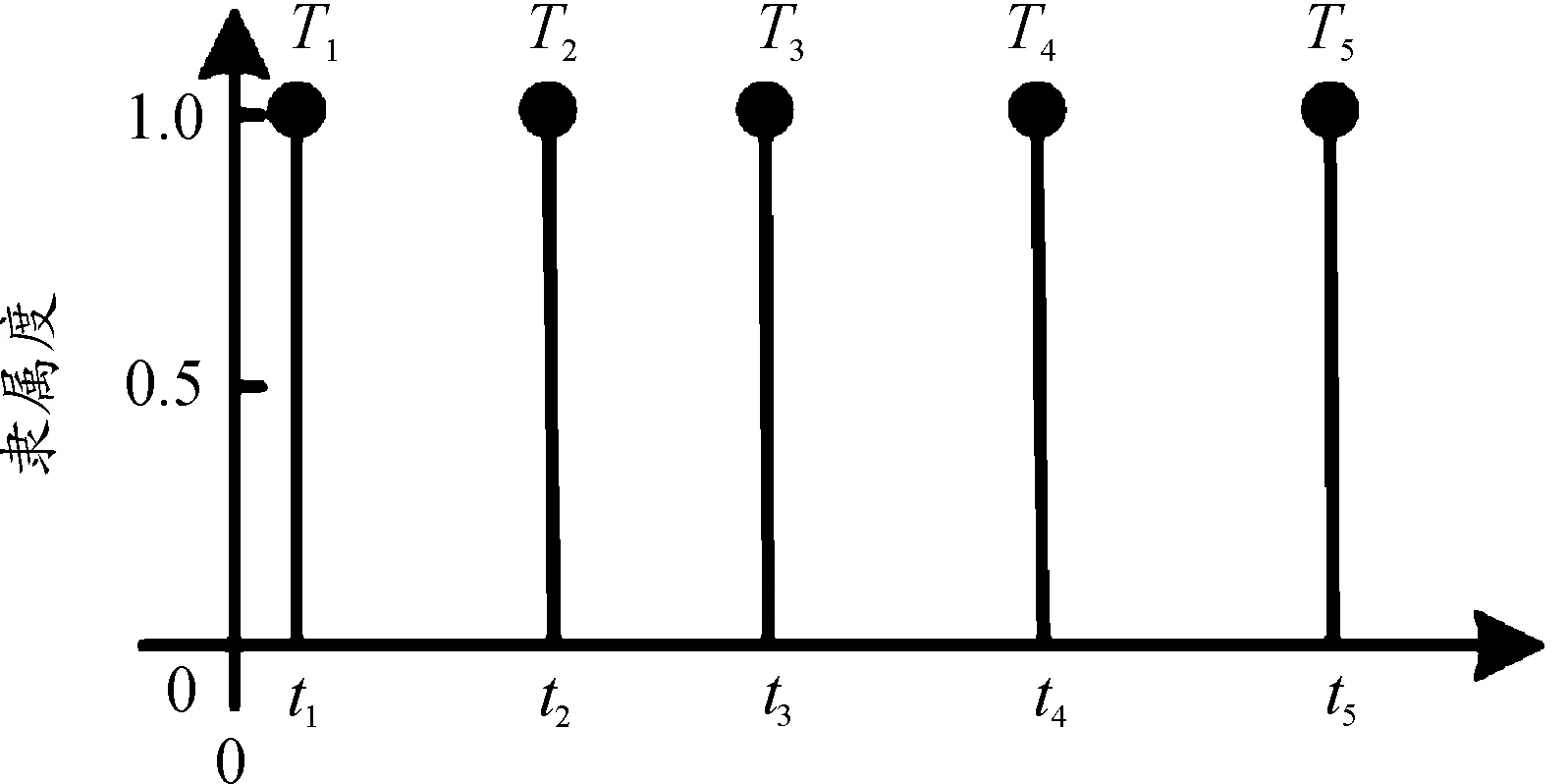
图7 输出解模糊隶属度函数
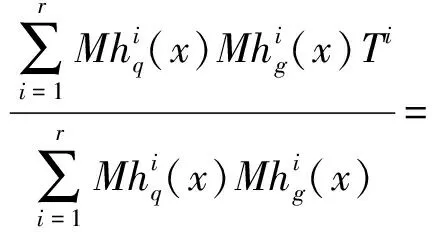
(25)

(26)
结合式(16)将强跟踪因子替换为修正后的强跟踪因子,具体公式为:
(27)
3 硬件在环实验验证
为验证提出的路面附着系数估计算法,利用控制器在环试验台进行测试。该试验台分别由180°全视镜投屏系统、6自由度平台、Car-Realtime高精度车辆模型、场景软件和控制器等多个部分组成,如图8(a)(b)所示。场景软件为驾驶员提供了高度逼真的场景,6自由度平台提供了相应的体感,利用该试验台能够较好地还原真实的测试场景,同时避免了一些危险工况在实车试验时的危险性。

图8 硬件在环试验台
测试工况设置如下:选用蛇形试验中锥桶的布置方案作为本文的测试场景,如图8(c)所示,该行驶轨迹能较好地反映车辆在侧向加速度连续变化时路面附着系数估计的响应特性,由此验证所研究的估计算法在车辆激励条件连续变化工况下的有效性和准确性。车辆行驶速度由试验台架上驾驶员决定,模拟真实交通环境。车速的变化范围约为65~90 km/h,采样步长为0.01 s。硬件在环试验台中车辆模型参数及标定关键参数如表2所示。
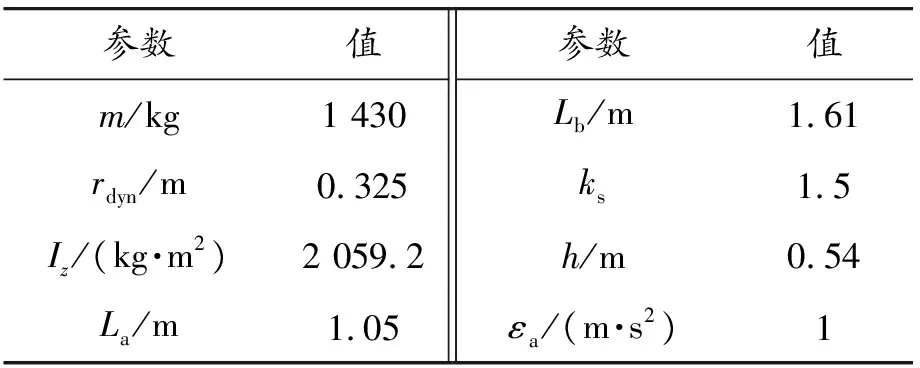
表2 算法参数
图9为整个实验过程中车辆纵向速度的变化过程。由图中可以发现:车辆在10~15 s时,从18 m/s加速到24.5 m/s;在15~35 s时,车辆近乎匀减速运动;在35~38 s时,进行加速运动。由此可知车辆在进行蛇形的时候,纵向加速度近乎为0 m/s2。识别路面附着系数的激励主要来自于车辆的侧向运动。

图9 纵向车速真实值
图10为整个实验过程中车辆横摆角速度的变化曲线,其中可以发现车辆约为从13 s附近驾驶员开始转动方向盘(见图11)进行横摆运动,同时从图10和图12中可以发现,车辆的横摆运动的侧向加速度和横摆角速度的幅值逐渐减少,对应于路面附着系数估计算法来说,车辆侧向运动的激励程度不断降低。
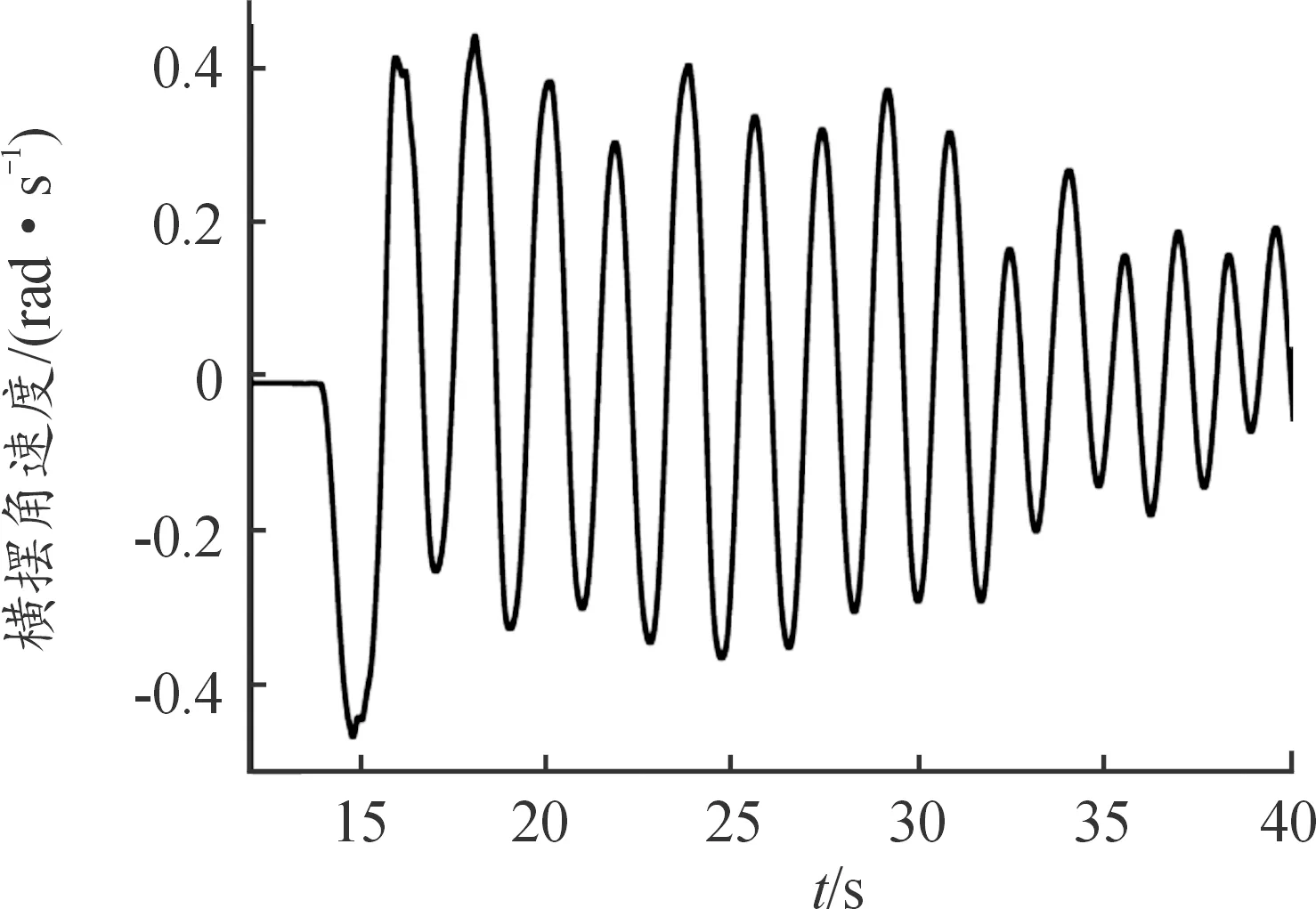
图10 横摆角速度真实值
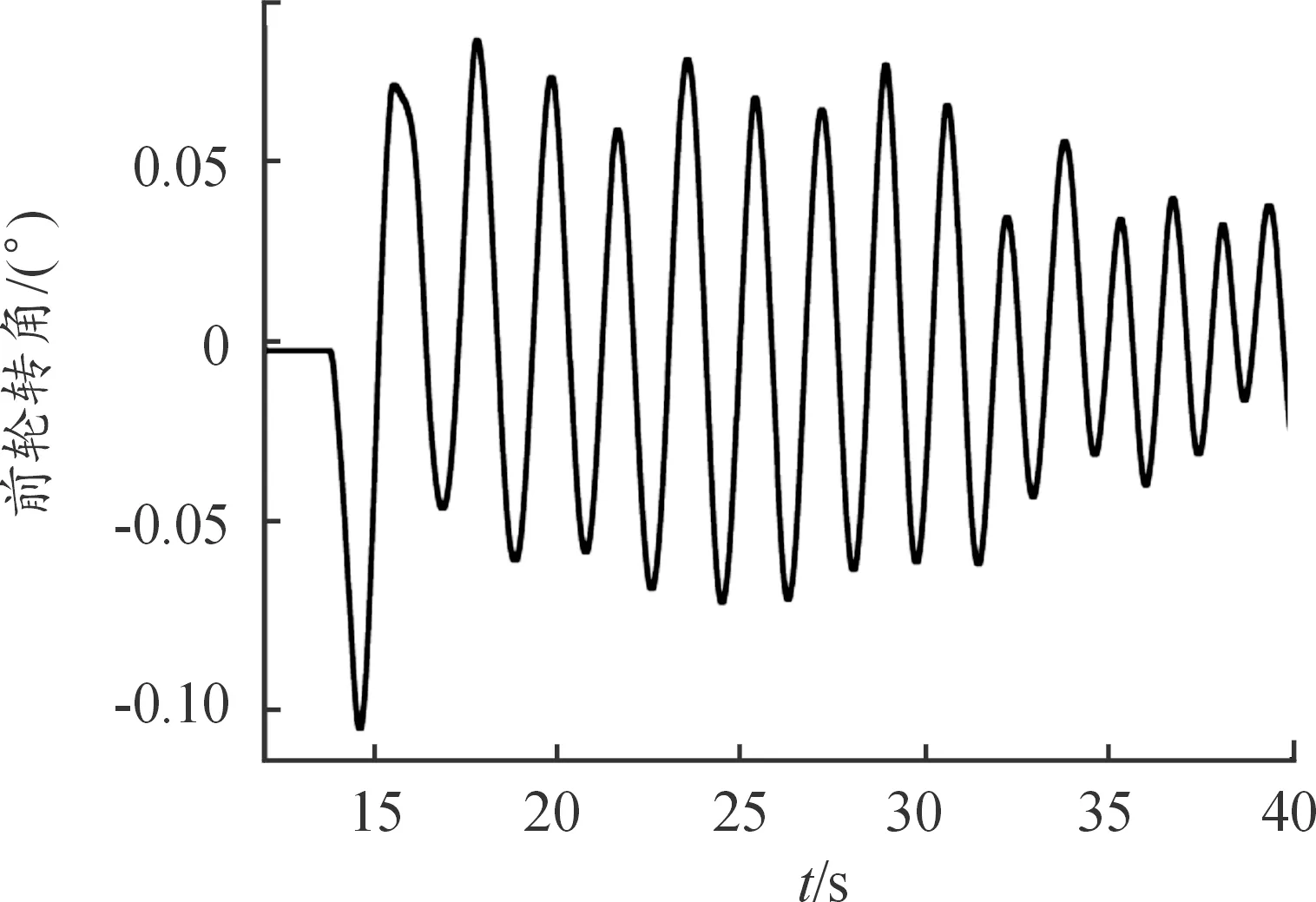
图11 前轮转角真实值
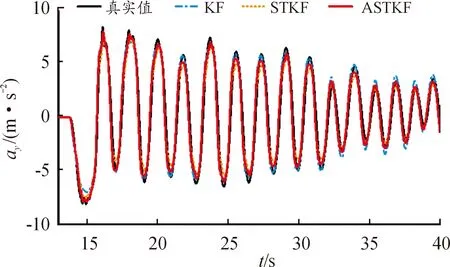
图12 侧向加速度估计值与真实值
为了验证提出算法的有效性,本文中提出的算法分别与标准卡尔曼滤波估计器和强跟踪卡尔曼滤波估计器进行了对比分析。图12—14为3种方法在上述工况下的估计效果。其中,KF表示标准卡尔曼滤波估计器,STKF表示强跟踪卡尔曼滤波估计器,ASTKF表示本文所提出的估计方法。
图13为3种不同方法估计路面附着系数的效果图,该路面附着系数的真实值为0.85。由于强跟踪因子和工况激励因子对于标准KF方法的改进使得在图中15 s处,3种方法在大激励程度下,本文所提出的算法的收敛速度最快且准确度最高,其次为STKF。然而,STKF未考虑当前工况的激励程度,强跟踪侧向加速度和纵向加速度,导致在小加速度情况下,估计算法得到的路面附着系数不准确,进而造成了STKF得到的路面附着系数估计值一直在大幅度震荡。
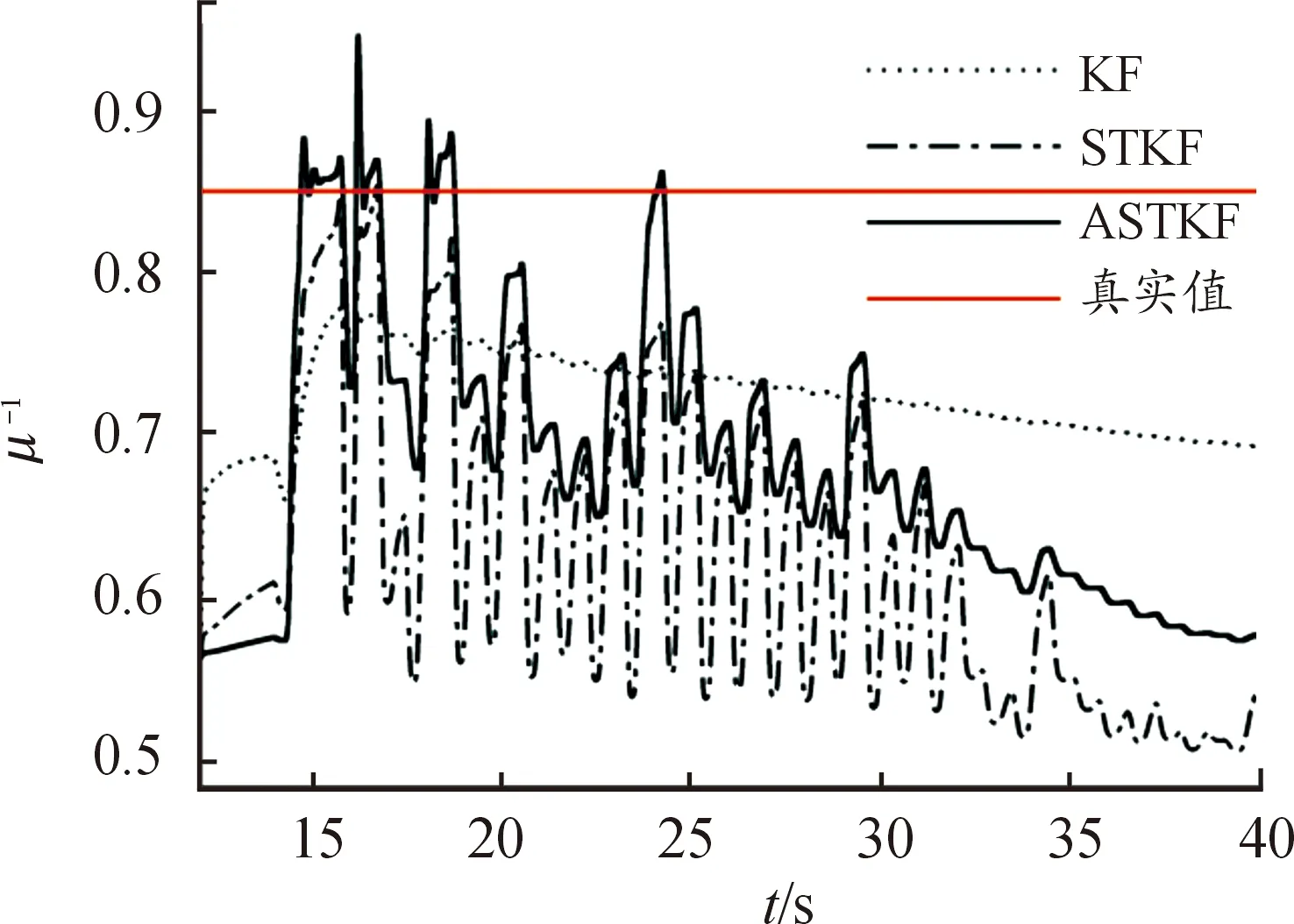
图13 路面附着系数估计值与真实值
由于ASTKF考虑了当前工况下的激励程度,并基于工况激励因子和强跟踪因子利用模糊推理系统对强跟踪因子进行抑制或增加,保证在小激励程度下估计参数的波动较小,以及大激励情况下估计参数的收敛性和准确性。同时可以发现随着车辆侧向加速度幅值的降低,3种方法得到的路面附着系数估计值都出现了一定程度的下降,发生该现象的主要原因有车辆状态激励程度的降低和车辆模型的建模误差。车辆侧向加速度与轮胎侧向力呈正相关,由图1可知,随着轮胎侧向力的降低,同一侧偏角所产生的侧向力差别不大,想要识别出准确的路面附着系数则需要更加精确的轮胎模型参数。然而,驾驶过程中轮胎模型参数受到载荷、路面条件和轮速等多方面因素影响,难以得到准确的轮胎模型参数。随着激励程度的降低,车辆建模误差对路面附着系数估计精度的影响显著增加,导致了行程后半段路面附着系数估计值误差的增加的现象。该现象表明了识别路面附着系数需要足够的激励程度才能保证识别算法的收敛速度和识别精度。
图12为3种方法估计的侧向加速度和真实值曲线,可以发现3种方法均能跟随上侧向加速度的变化,但是在大加速度情况下,ASTKF估计得到的侧向加速度的精度最高。图14为3种方法估计的纵向加速度和真实值曲线,可以发现3种方法均能跟随上侧向加速度的变化,但是在大加速度情况下,KF估计得到的纵向加速度的精度最高。从图13也可以看出,在10~15 s处KF算法估计的路面附着系数最大且接近于真实值。

图14 纵向加速度估计值与真实值曲线
仿真结果表明:提出的基于模糊工况自适应强跟踪卡尔曼滤波的路面附着系数估计算法,根据车辆状态的激励程度和强跟踪因子能够提高估计方法在大激励程度时的收敛速度,同时降低了小激励程度时估计值的波动幅值。模糊推理系统根据2个因子的推理出当前工况对于强跟踪因子的抑制程度,防止估计算法在小激励情况下估计值出现震荡的问题。相比于标准卡尔曼滤波估计器提升了估计器的收敛速度,使得估计算法能够快速跟踪上由于路面条件变化导致的路面附着系数突变。
4 结论
针对路面条件和车辆激励程度不确定性导致路面附着系数估计算法精度下降,采用模糊推理方法建立了综合考虑车辆激励条件和路面条件突变的自适应强跟踪卡尔曼滤波估计器。该估计器能够根据当前车辆状态实时修正强跟踪因子,防止在小激励条件下产生较大的强跟踪因子,避免路面附着系数出现振荡。通过硬件在环试验台上驾驶员进行的蛇形试验工况验证了该算法能够有效地提升路面附着系数估计方法收敛速度和识别精度,相较于强跟踪卡尔曼滤波(STKF),根据车辆状态激励程度对强跟踪因子进行修正,实现了估计方法的收敛速度和估计值波动幅值之间的平衡。
随着车辆侧向加速度幅值不断降低,3种方法估计的路面附着系数也随之降低。因为随着激励条件的降低,车辆模型建模误差对于路面附着系数估计的影响被放大,并且由于在轮胎线性区时路面附着系数对于轮胎力的影响较弱,进而导致了估计的路面附着系数降低。该现象说明路面附着系数估计需要足够的车辆状态激励才能逼近真实值。
采用了模糊推理系统综合考虑车辆状态激励对于强跟踪因子的影响,避免了在小激励条件下路面附着系数估计值的振荡。未来的研究方向为拓宽路面附着系数准确识别的范围,即轮胎力未饱和时提高路面附着系数的识别精度。关于该方向的建议为进一步研究如何降低车辆模型建模误差,进而降低路面附着系数所需的激励条件。

