Enhanced LSTM Model for Daily Runoff Prediction in the Upper Huai River Basin, China
Yunyun Mn, Qinli Yng,b,*, Junming Sho, Guoqing Wng, Linlong Bi, Yunhong Xu
a School of Resources and Environment, University of Electronic Science and Technology of China, Chengdu 611731, China
b Yangtze Delta Region Institute (Huzhou), University of Electronic Science and Technology of China, Huzhou 313001, China
c School of Computer Science and Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China
d State Key Laboratory of Hydrology–Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China
e Xinyang Hydrology and Water Resources Survey Bureau, Xinyang 450003, China
Keywords:Runoff prediction Long short-term memory Upper Huai River Basin Extreme runoff Loss function
ARTICLEINFO Runoff prediction is of great significance to flood defense.However, due to the complexity and randomness of the runoff process, it is hard to predict daily runoff accurately, especially for peak runoff.To address this issue, this study proposes an enhanced long short-term memory (LSTM) model for runoff prediction, where novel loss functions are introduced and feature extractors are integrated.Two loss functions (peak error tanh (PET), peak error swish (PES)) are designed to strengthen the importance of the peak runoff’s prediction while weakening the weight of the normal runoff’s prediction.The feature extractor consisting of three LSTM networks is established for each meteorological station, aiming to extract temporal features of the input data at each station.Taking the upper Huai River Basin in China as a case study,daily runoff from 1960 to 2016 is predicted using the enhanced LSTM model.Results indicate that the enhanced LSTM model performed well,achieving Nash–Sutcliffe efficiency(NSE)coefficient ranging from 0.917 to 0.924 during the validation period(November 2005–December 2016),outperforming the widely used lumped hydrological models(Australian Water Balance Model(AWBM),Sacramento,SimHyd, and Tank Model) and the data-driven models (artificial neural network (ANN), support vector regression (SVR), and gated recurrent units (GRUs)).The enhanced LSTM with PES as loss function performed best on extreme runoff prediction with a mean NSE for floods of 0.873.In addition,precipitation at a meteorological station with a higher altitude contributes more runoff prediction than the closest stations.This study provides an effective tool for daily runoff prediction,which will benefit the basin’s flood defense and water security management.
1.Introduction
Among all the natural disasters,flood is the most frequent type,and it endangers the population and property[1–3].Floods are also increasing in frequency and intensity due to climate change and human activities[4].Since ancient times,human beings have made considerable efforts to combat floods, including structural and non-structural methods [5].Structural methods are the most visible flood defense measures,such as levees,bunds,dams,and weirs.Meanwhile, the non-structural methods like flood forecasting models and systems, which facilitate disaster preparedness planning, have played prominent roles in flood risk mitigation.With the development of computer science and hydrological science in recent decades, flood prediction models have been leveraged worldwide to tackle the flood issue.However,due to its complexity and nonlinearity, flood prediction is a non-trivial task that demands advanced models and higher accuracy.
In general, runoff prediction and flood forecast models can be categorized into process-based and data-driven models [6,7].The process-based model, which dates back to the 1960s, is a mathematical formulation that explicitly represents the hydrologic state variables and fluxes.Up to the present, numerous process-based hydrological models,including lumped and distributed types,have been proposed and widely applied in runoff prediction [8].For instance, TOPMODEL is one of the models to explicitly use topographic data to reflect a basin’s hydrological response characteristics in the model formulation[9].It was used for runoff prediction in different regions [10,11].The Soil and Water Assessment Tool(SWAT)[12],a semi-distributed hydrological model,has undergone sustaining development since its establishment.Diverse modules such as radar precipitation [13], groundwater units [14], and snowmelt units [15] have been successively integrated.SWAT model performed well on runoff prediction [16,17].Australian Water Balance Model(AWBM)is a lumped hydrological model that can use daily rainfall to estimate daily runoff [18,19].Despite their widespread applications and advantage on interpretability, process-based models still have some drawbacks on flood prediction, such as over-parameterization, high complexity,a wealth of expert knowledge, and high requirements for data.
Alternatively, the data-driven models based on statistical theory can learn the relationships among influencing factors and runoff automatically, which is not only cost-effective but also highly efficient.A large number of data-driven models for runoff prediction have been proposed and applied in practices [20], including artificial neural network (ANN) [21], support vector machine(SVM) [22], neuro-fuzzy [23], adaptive neuro-fuzzy inference system(ANFIS)[24],wavelet neural network[25],and multilayer perceptron(MLP),and the like.Among them,ANN is the most popular data-driven model for runoff prediction with good generalization ability and relatively high accuracy among all the models mentioned above.However, it fails in modeling the time dependency of data sequences and predicting the peak value accurately.Time dependency refers to the autocorrelation relationship between the previous data and the current data in a time series, which are often difficult to express directly in equations[26].In comparison,the long short-term memory (LSTM) model with a gated mechanism stands out due to its excellent performance, simple architecture, and superior time dependency ability.
LSTM is a deep learning model proposed by Hochreiter and Schmidhuber [27] to solve the complexity of information storing in the long sequence backpropagation process.Because of the outstanding performance on long sequence tasks, LSTM has been widely applied in various fields since its inception,especially in time series.In recent years,LSTM has attracted much attention in hydrology[28–32].For instance,Kratzer et al.[33]studied runoff prediction using LSTM in 241 catchments in the Catchment Attributes and Meteorology for Large-sample Studies (CAMELS) data set and proved that LSTM could get good simulation results in most basins.Meanwhile,the effectiveness of LSTM in watershed-scale transformation is also verified, which shows the great potential of LSTM.However,peak flow prediction is still a challenge for LSTM[34,35].
The challenge of peak flow prediction mainly lies in two aspects.One is how to identify the important input features for runoff prediction.The other is how to optimize the model’s objective function to achieve good prediction results.Although the LSTM model can capture the temporal features of the input data series(e.g., rainfall), it ignores the spatial heterogeneity of the temporal features.Actually, in practice, the impacts of different rain gauges on runoff prediction are different.Therefore, the structure of the LSTM model needs to be modified and improved.LSTM generally takes mean square error (MSE) as the loss function regarding model optimization.However, MSE treats samples with different prediction errors equally,which fails to emphasize the importance of peak flow prediction.Ding et al.[36]used extreme value theory to design a novel loss function (extreme value loss (EVL)) in the extreme events model, whose main idea is to adjust the weights on extreme events so that the model pays more attention to extreme values in the parameter optimization process.Therefore,new loss functions can be designed for LSTM to improve its ability to deal with peak flow prediction.
Accurate flood prediction for the upper Huai River Basin is significant for flood management of the whole Huai River Basin.The Huai River, one of the seven major rivers in China, is located in eastern China between the Yangtze River and Yellow River.Due to its continental monsoon climate with a complex and variable atmospheric system,the Huai River Basin is prone to flood,suffering floods about once per two years [37].The upper Huai River Basin is the essential control basin for the upper Huai River.In the past few decades,many efforts have been made on runoff prediction in the upper Huai River Basin.For instance, Liu et al.[38]used the fully distributed model Topographic Kinematic Approximation and Integration (TOPKAPI) to predict runoff with a sixhour time step.Lv et al.[39]constructed an LSTM model for cyclic prediction and achieved good results for hourly flood forecasting.However,most existing studies are fragmented,focusing on hourly runoff prediction or flood events analysis relatively quickly but lack continuous daily runoff prediction over a long period.Furthermore, in the context of climate change, population growth, and economic development, the upper Huai River Basin has experienced significant climate change and land-use change over the past few decades [40,41].Runoff prediction in the changing environment in the upper Huai River Basin is in high demand.
This study aims to propose an enhanced LSTM model to improve the accuracy of daily runoff prediction to facilitate flood defense.The objectives are as follows: ①to explore the trends of the hydro-meteorological variables and land use in the upper Huai River Basin in the last decades;②to predict runoff and flood in the upper Huai River Basin by using a structurally improved LSTM with novel loss functions designed for peak flows; and ③to compare the improved LSTM model with different existing models to proof its outperformance on runoff prediction in the study area.
2.Study area and data acquisition
2.1.Study area
The Huai River,one of the seven large rivers in China,is located in the east of China and originates from Henan Province.The basin located in the upper stream of the Huai River above Xixian County(upper Huai River Basin) with a drainage area of 10 190 km2is selected as the study area.The basin is the subtropical monsoon humid climate zone, with an average temperature of 15.43 °C.Monsoon mainly affects precipitation,with an average annual precipitation of 1043 mm, 50% concentrated from June to September.The drainage system of the basin is distributed in a dendritic form,and the average runoff depth is about 350 mm.The basin topography is high in the west and low in the east,with an average elevation of 47 m.Most of the land in the basin is cultivated, with a small number of cities and woodland.Six meteorological stations covering the spatial heterogeneity were set up in/around the basin.Meteorological stations numbered 57285 and 57390 are located at the upstream of the basin,stations 57297 and 57298 are located in the middle reaches of the region,station 57295 is beside the northern boundary of the basin, while station 57296 is located at the outlet of the upper Huai River.
2.2.Data acquisition
Climatic data, including daily precipitation, pan evaporation,and temperature from 1951 to 2016,were collected from the China Meteorological Data Service Center†† https://data.cma.cn.‡ https://glovis.usgs.gov..Daily runoff (m3·s-1) during 1951–2016 at the Xixian County hydrometric station was provided by Henan Hydrology Bureau.The SRTM1 DEM data‡† https://data.cma.cn.‡ https://glovis.usgs.gov.with a spatial resolution of 30 m was used in this study.Landsat 5 Thematic Mapper (TM) Collection 1 Level-1 data was used for land use classification of the study area in 1987, and Landsat 8 Operational Land Imager(OLI)Collection 1 Level-1 data was used for that in 2016.
3.Methodology
The non-parametric rank-based Mann–Kendall test (recommended by the World Meteorological Organization)[42]and linear regression method are applied to identify the trends of meteorological and hydrological variables.The basic structure of the LSTM model is introduced in Section 3.1 before presenting the enhanced LSTM model(Section 3.2).For comparison with the existing methods, representative models are selected and briefly introduced in Section 3.3.In evaluating the performances of different models,specific evaluation metrics are finally presented at the end of this section.
3.1.LSTM network
LSTM is developed from the recurrent neural network (RNN)[43].Compared with RNN, LSTM adds a forgetting mechanism,which can also solve the gradient explosion problem.In the structure of LSTM(as shown in Fig.1),a particular unit called a memory cell is similar to an accumulator and a gated neuron.The next sequential step has a parallel weight and copies its state’s actual value and accumulation.The LSTM has a self-connection mechanism controlled by a multiplication gate that learns and decides when to clear the memory content by another unit.For better understanding, define time as subscript t, hidden state as h, cell state as C,input as x,the output of input gate as i,the output of forget gate as f, the output of output gate as o, and the output of the reserved portion of the original loop layer as ^C.σ is an activation function, such as sigmoid and Rectified Linear Unit (ReLU).
LSTM comprises three gates:input gate,output gate,and forget gate.Its forward propagation process can be expressed by Eqs.(1)–(3):
Input gate:
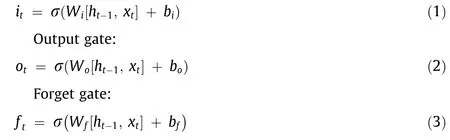
The cell information Ctand the hidden information htare updated by Eqs.(4)–(6):

Fig.1.The structure of the LSTM model.The subscript ‘‘t” here represents the current time, ht-1 and Ct-1 represent the hidden state and cell state respectively received from the previous node.In other words, C and h represent long-term and short-term changes, respectively.The rest are intermediate variables.
where W is the weight matrix and b is the bias,which are updated and optimized in the training process.
Compared with RNN, after adding the forgetting mechanism ft,the LSTM no longer passes all the historical information backward but selectively forgets part of the historical content, memorizes part of the historical context, and adds new input information to the backward transfer.Then it uses the backpropagation algorithm[44] to update the parameters and optimize the model.
3.2.Enhanced LSTM model for runoff prediction
3.2.1.Integrating feature extractor into the LSTM model
The flowchart of the enhanced LSTM model is illustrated in Fig.2.It includes four layers:input layer,feature extractor,predictor, and output layer.Unlike the original LSTM model, the enhanced LSTM model has an integrated feature extractor.The motivation of this integration is to identify the critical features for the runoff prediction task.For this current work,a separate feature extractor is proposed for each meteorological station at Xixian County hydrometric station, assuming that precipitation at different stations might contribute to different runoff generation.
A feature extractor is composed of three LSTMs.Specifically, it takes precipitation(P), conditional cumulative precipitation (CCP),and runoff with a step length (τ days) before the time t as the input features.It also takes the historical period feature’s runoff data of the same period last year.The first two LSTMs are used to extract long-term trend features and short-term change features, respectively.Then, the two parts of the extracted features are spliced together to output site features through the third LSTM.
Subsequently,the output features of each station obtained from each feature extractor and the historical runoff with a step length of τ are spliced together using a residual connection technique.Finally,an LSTM is used to predict runoff at time t.Historical runoff provides constraints for boundary conditions,breaks the network’s symmetry, and improves the characterization ability of the network [45,46].
3.2.2.Designing new loss functions to improve peak runoff prediction
The MSE is generally used as the loss function for typical regression problems.The formula is as follows:

The above formulation indicates that MSE treats runoff prediction errors equally no matter the runoff prediction error, either high or low.However,the peak runoff prediction error is a concern in flood forecasting,and the normal runoff prediction error is relatively unimportant.To solve this problem, two new loss functions are designed to increase the importance of peak loss to improve the accuracy of peak runoff prediction.
(1)Peak error tanh(PET).Since the error of the extreme value is more significant than that of the normal flow,the weight can be increased for the larger error in the MSE.Therefore,a tanh function is added alongside the MSE to amplify larger errors and reduce small errors simultaneously.The formula is as follows:

Fig.2.The framework of the enhanced LSTM model for daily runoff prediction.
Its function curve is shown in Fig.3.When the independent variable is larger, the function value is also larger;when the independent variable is smaller, the function value will correspondingly become smaller.Therefore, the purpose of amplifying large errors and reducing small errors is achieved.
(2) Peak error swish (PES).Swish is a new activation function proposed by Google [47].Swish is adapted to local response normalization, and the effect of fully connected layers above 40 is much better than other activation functions.Furthermore, it has shown better performance than the current best activation function on different data sets.The Swish function image is shown in Fig.4.
The expression of PES after fusing MSE is
3.2.3.The training of the enhanced LSTM model
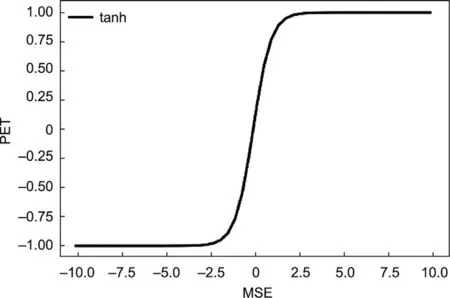
Fig.3.tanh function graph.
The enhanced LSTM model training adopts the mini-batch training technique.A batch size of 64, epoch size of 200, and the Adam optimizer are used for training the model.Three loss functions, MSE, PET, and PES are used.To keep the features of each input data within the same numerical range,the data is normalized by using Eq.(10) as follows:
where X is the variable, Xminand Xmaxare the minimum and maximum values of the variable X,respectively.Xnormrepresents the normalized data.
3.3.Selected comparative models for runoff prediction
In verifying, the effectiveness of the enhanced LSTM model on daily runoff prediction, three data-driven models (support vector regression (SVR),ANN,and gated recurrent units (GRUs))and four lumped hydrologic models(AWBM,Sacramento,SimHyd,and Tank Model) are selected for comparison.

Fig.4.Swish function graph.
SVR is an important application of SVM[22]in regression tasks.SVR works by finding a regression plane so that all the data in a set are closest to that plane.To achieve the regression task of nonlinear data,SVR can also use a nonlinear kernel to get a hyperplane to fit the data.SVR is favored for its simplicity,efficiency,and superior performance.The ANN model is an information processing system that mimics brain functions according to biological neural networks[21,48].It consists of the input layer,hidden layers,and output layer.As one of the classical machine learning models,it is also the basis for most deep learning models.Due to the high flexibility of ANN structure,suitable network structure and loss function can be designed according to the specific applications.ANN learning is robust to errors in training data and has been successfully applied to many fields.
GRU is a type of RNN [49].In many cases, it performs similarly to LSTM, but it is easier to train and essentially improves training efficiency.SVR and ANN are both widely used and representative traditional data-driven models.To verify the advance of the proposed model over the traditional data-driven methods, SVR and ANN are selected for comparison.In addition, comparing the proposed model with GRU, which has a similar effect with LSTM,can indicate the structural superiority of the enhanced LSTM.
The AWBM is a catchment water balance model that links rainfall and evapotranspiration to runoff through daily or sub-daily data[18].It calculates rainfall losses for flood hydrological models.The model contains five stores, including three surface stores, a base flow store, and a surface runoff routing store.Sacramento model is a lumped catchment water balance model with 16 parameters and performs at a daily time step[50].The runoff production can be divided into five parts: direct runoff, surface runoff, soil flow, fast groundwater, and slow groundwater.A linear reservoir simulated medium flow,fast groundwater,and slow groundwater.SimHyd is a conceptual rainfall-runoff model with seven parameters containing three stores for interception loss, soil moisture,and groundwater [51].Sugawara et al.[52] developed the tank model to explain a catchment’s water flow phenomena.It is a straightforward model, composing four tanks placed vertically in series.The precipitation is poured into the top tank, and evaporation is subtracted from the top tank downward.As each tank is emptied,the evaporation gap begins at the next tank until all tanks have been emptied.The output of the side outlets is the calculated runoff [53].The four classical lumped hydrological models have been successfully applied worldwide in catchment runoff simulation and prediction.Comparison with the selected lumped hydrological models intends to verify the superiority of the proposed model over the traditional physical models.
3.4.Evaluation metrics
To evaluate the performance of different(environmental)models,please refer to the literature published by Bennett et al.[54].In this study, the Nash–Sutcliffe model efficiency (NSE) coefficient,mean absolute error (MAE), root mean square error (RMSE), relative volume error (RE), qualification rate (QR), and NSEfloodare selected as the evaluation criteria.QR refers to the forecast flood QR [55].NSEfloodrefers to the average NSE for forecasting floods(Eqs.(11)–(16)).

4.Results and discussion
4.1.Trends of the hydro-meteorological variables
In exploring the trends of meteorological and hydrological elements in the study area, precipitation, runoff depth, temperature,and pan evaporation during 1951–2016 are analyzed on annual and seasonal scales using the Mann–Kendall method and linear regression method.The statistical results are shown in Table 1.In addition, Fig.5 illustrates the inter-annual changes of these hydro-meteorological variables.
In general, it can be seen that precipitation and runoff depth have insignificant decreasing trends on the annual scale in the upper Huai River Basin.The temperature has a clear upward trend(0.18°C per ten years),relatively lower than the average temperature increase rate (0.24 °C per ten years) in China during 1951–2018 [56].Fig.5(b) shows that the annual pan evaporation has a significant downward trend(3.96 mm per year).Similar to findings in Han et al.[57], the evaporation paradox existed in the upper Huai River Basin,which can be attributed to changes in solar radiation, relative humidity, and wind speed.

Table 1Statistical information of trend analysis for the hydro-meteorological variables on annual and seasonal scales during 1951 and 2016 for the upper Huai River Basin, China.

Fig.5.The inter-annual change of hydro-meteorological variables.(a)P and runoff depth; (b) temperature and pan evaporation during 1951 and 2016 for the upper Huai River Basin, China.
Specifically,consistent with annual precipitation,precipitation in spring and autumn shows insignificant downward trends,while precipitation in summer and winter shows insignificant upward trends.Except for runoff depth in winter(insignificant increase),the trend of seasonal runoff depth is consistent with that on the annual scale(insignificant decrease).The seasonal temperature has risen significantly except for autumn.The trend of pan evaporation on the seasonal scale is consistent with that on the annual scale, but the decreasing trend in summer(0.41 mm per year)is not significant.
In addition, the number of days for different intensities of precipitation is also studied(as shown in Table 1).The number of rainfall days (P >0) shows a downward trend at the 95% confidence level and remains consistent on the seasonal scale, especially in summer and winter.The number of days with rainfall greater than 25 and 50 mm mainly showed a downward trend on the annual and seasonal scales.The annual maximum rainfall also changed insignificantly.Therefore,extreme precipitation events in the basin did not show a noticeable change in the context of climate change.
Overall, the above results reveal that from 1951 to 2016, the temperature in the upper Huai River Basin increased significantly,the pan evaporation decreased significantly, and the precipitation and runoff were stable.Although the hydro-meteorological variables change, the hydrological status remains stable in the upper Huai River in general.
4.2.Land use change in the upper Huai River Basin
Besides climate change,land use change is another critical driving factor for the hydrological cycle.For instance, land use change may influence runoff generation and formation processes via changing the characteristics of the underlying surface.Different land change patterns (e.g., afforestation, deforestation, urbanization) exert different impacts on runoff.In recent decades, land use change in the upper Huai River Basin needs to be investigated to better understand the impact of land use on runoff change.To this end, we classified land use in the upper Huai River Basin into five types (water body, forest, residential area, farmland, and bare land).We analyzed the land use status in 1987 and 2016 based on Landsat images using the random forest algorithm.The land use classification results in 1987 and 2016 are shown in Appendix A Fig.S1, and the transfer matrix of land use change from 1987 to 2016 is presented in Table 2.
Intuitively, Fig.S1 shows that the area of farmland has decreased, while the residential area and forest cover have expanded obviously.Quantitatively,the area of farmland has been reduced by about 1100 km2in various forms, mainly converted to residential area and forest land.The residential area has expanded by about 180 km2,which increases the impervious surface area and may result in urban flooding.The decrease of farmland area and the increase of forest (about 780 km2) is consistent with the‘‘returning cropland to the forest” initiative proposed by the Chinese government.The initiative aims to protect the ecological environment while developing the economy.As forests play important roles in regulating rainfall and reducing flood peaks,the increase of the forest area may lead to more water for water conservation while less water for flooding.
4.3.Runoff prediction based on the enhanced LSTM model
As precipitation data at some meteorological stations are missing during 1951 and 1959, daily runoff during 1960 and 2016 is selected for the upper Huai River Basin prediction framework based on the enhanced LSTM model.Specifically, data during January 1960–October 2005 are used for training and the remaining data(November 2005–December 2016)for testing.To predict daily runoff at the day (d), the input data, precipitation(Pd-6, Pd-5,..., Pd-1), conditional cumulative precipitation(CCPd-6, CCPd-5,..., CCPd-1, cumulative days are two days), runoff(Rd-6, Rd-5,..., Rd-1), and runoff data at the same time last year are used.CCP means accumulated precipitation over specified days.For instance, CCPd-1with two cumulative days represents the accumulated precipitation of the day d-1 and the day d-2.The performances of the enhanced LSTM models on daily runoff prediction are listed in Table 3.It can be noticed that the NSE of overall runoff prediction based on the enhanced LSTM models all exceeds 91%.Notably, the improved LSTM model with the loss function of PET shows the best performance, achieving an NSE of 0.924, as demonstrated in Fig.6.
To further assess the performance of the enhanced LSTM model on extreme runoff(flood)prediction,QR and NSEfloodare calculated and presented in Table 3.Here,only a peak flow rate more than or equal to 1000 m3·s-1is regarded as a flood event.As a result, 13 flood events were identified in the test dataset.It can be found from Table 3 that the improved LSTM with PES as loss function performed best, achieving a QR of 92.3% and NSEflood(average NSE during the flood period) of 0.873.Based on this model, Fig.7 displays the prediction results of nine representative flood events.
In evaluating the contributions of precipitation at different meteorological stations to runoff prediction, the Pearson correlation coefficient (PCC) was calculated between the extracted sitefeature(output of feature extractor for each meteorological station in Fig.1) and the predicted runoff during the test period (November 2005–December 2016).The results are shown in Table 4.The higher the PCC is, the more influential the feature is to runoff prediction.

Table 2Transition matrix of land use changes from 1987 to 2016 for the upper Huai River Basin, China (km2).
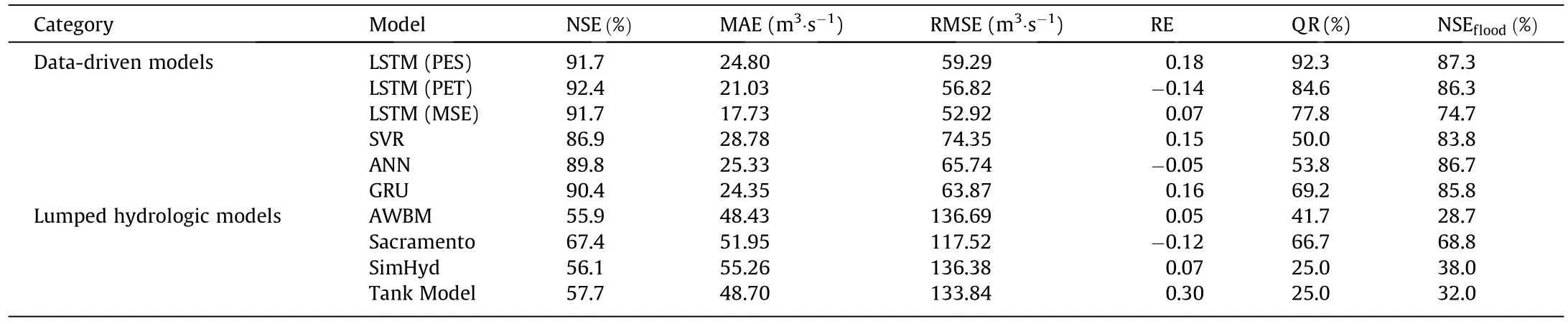
Table 3Performance comparison of different runoff prediction models.

Fig.6.The observed and predicted runoff based on the enchanted LSTM model with PET as loss function during November 2005–December 2016 for the upper Huai River Basin, China.
Table 4 indicates that the extracted site features have negative correlations with predicted runoff when the loss functions of the model are MSE and PES.In contrast, their correlations are positive when PET is used as the loss function.The absolute value of the correlation coefficient is the most crucial information,representing the correlation between the features extracted from the meteorological station and the predicted runoff.The data in bold indicates the strongest correlation.The positive and negative signs are determined by the parameter training process inside the model, working in coordination with the whole model and eliminating the effect of the sign within the model itself.It can be seen that PES significantly improves the correlation coefficient between site features and predicted runoff, with the highest PCC of -0.672 at station 57285.Besides,meteorological stations with high altitudes contribute to runoff prediction than those closer to the hydrometric station.For instance, stations 57390 and 57285, which are the first and second highest altitudes, have relatively higher PCC than those closer to the hydrometric station.
4.4.Comparison with the selected comparative models
The performances of different models are shown in Table 3.In general, the data-driven models outperformed the lumped hydrological models on daily runoff prediction.The enhanced LSTM model achieved better results than comparative models such as SVR, ANN, and GRU among the data-driven models.Although GRU has a simpler structure and higher training efficiency,its overall performance is slightly lower than the enhanced LSTM.Their discrepancy in performance is even more apparent in the flood forecasting results,which indicates that the enhanced LSTM model structure and the two loss functions(PET and PES) have improved the model’s ability to predict runoff and flood.Specifically, for the overall runoff, the LSTM model with PET as loss function exhibits the highest NSE of 0.924.However, regarding the flood peak prediction, with the highest QR of 92.3% and the highest NSEfloodof 0.873, the enhanced LSTM with PES performed much better than the other comparison models.The above results imply that the enhanced LSTM model with PES as a loss function has more significant potential for flood forecasting.

Fig.7.Performance evaluation on peak runoff prediction based on the improved LSTM with PES as loss function for the upper Huai River Basin, China.

Table 4PCC between the extracted site features and runoff predictions with different loss functions.
In the training process,data is firstly normalized.So MSE is usually between zero and one.There is no problem of output saturation for the PET loss function when there is a rapid rise stage,but the rising rate gradually decreases.One possible explanation is that PET magnifies MSE as a whole.The larger the MSE,the larger the PET (MSE is in the range of 0–1).Therefore, when the model optimizes the parameters,it is optimized as a whole,so the overall prediction result of runoff is better.When the horizontal axis is between zero and one, PES is approximately linear, but it is not.PES reduces the MSE, but the first derivative of PES gradually increases and approaches a constant value.Therefore, when the MSE is close to zero, the rising rate of PES is slower, and when the MSE is close to one,the increasing rate of PES is faster.The first derivative increasing monotonically may be why PES has a better effect on improving flood flow with more significant errors.
The floods in the upper reaches of the Huai River are concentrated from June to August,and most of them are caused by heavy rain, which brings enormous flood control pressure to the middle and lower reaches.To protect most social property and people’s safety, the middle and lower reaches of the Huai River have operated part of the flood storage areas mainly for agriculture and industry and built many reservoirs in the upper reaches.Enhanced LSTM can timely and accurately predict the arrival time of flood peak and the flow, which is significant to the operation of reservoirs and flood storage areas.On the other hand,the reservoirs also greatly influence runoff.Therefore, some of the prediction errors may be caused by the reservoirs.Future works could consider the impact of the reservoirs on runoff prediction.
5.Conclusions
To improve the accuracy of runoff prediction, this study proposed an enhanced LSTM model.Based on the original LSTM model, a feature extractor is designed for discriminative feature identification,and two novel loss functions(PET and PES)designed for flood peak prediction are also introduced.Taking the upper Huai River Basin as a case study, the enhanced LSTM model was applied and evaluated for daily runoff prediction during 1960–2016.
During the study period,the upper Huai River Basin has experienced a warmer and drier climate but a relatively stable hydrologic status.Land use has changed between 1987 and 2016,mainly from cropland to forest and residential areas.Results indicate that the enhanced LSTM performed well on daily runoff prediction(achieving the highest NSE of 0.924), outperforming the comparative models(i.e.,SVR,ANN,GRU,AWBM,Sacramento,SimHyd,and Tank Model).Regarding the flood peak prediction, the enhanced LSTM model with PES as loss function performed best with the QR of 92.3% and the NSE during the flood period (NSEflood) of 0.873.Furthermore,there is a correlation between the meteorological station’s extracted features and predicted runoff.The correlation reveals that precipitation at a station with a high elevation contributes more to runoff generation than those closer to the hydrometric station.This study provides an effective tool for daily runoff prediction, which would benefit the local basin’s flood risk management and water security.
Acknowledgments
This work was financially supported by the National Natural Science Foundation of China (52079026), the National Key Research and Development Program of China (2021YFC3201100),the National Natural Science Foundation of China (41830863 and 61976044), Sichuan Science and Technology Program(2020YFH0037),the Belt and Road Fund on Water and Sustainability of the State Key Laboratory of Hydrology–Water Resources and Hydraulic Engineering (2019nkzd02), the Open Research Fund of State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin(IWHR-SKL-201911),and the Fundamental Research Funds for the Central Universities (ZYGX2019Z014).Many thanks go to Mr.Cobbinah M.Bernard, who significantly contributed to the manuscript revision.
Compliance with ethics guidelines
Yuanyuan Man, Qinli Yang, Junming Shao, Guoqing Wang,Linlong Bai, and Yunhong Xue declare that they have no conflict of interest or financial conflicts to disclose.
Appendix A.Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.eng.2021.12.022.
- Engineering的其它文章
- Dynamic Deformation Measurement of an Intact Single Cell via Microfluidic Chip with Integrated Liquid Exchange
- The Rational Design and Development of Microalgae-Based Biohybrid Materials for Biomedical Applications
- DART Mission Shows Potential for Planetary Defense by Smashing Asteroid into New Orbit
- Electric Racers Hit the Track, but Still Catching Up
- Micro-Cantilever Electric Field Sensor Driven by Electrostatic Force
- Theory and Practice of Hydrodynamic Reconstruction in Plain River Networks

