Evaluation of the Impact of Multi-Source Uncertainties on Meteorological and Hydrological Ensemble Forecasting
Zhngkng Shu, Jinyun Zhng, Lin Wng, Junling Jin,*, Ningbo Cui, Guoqing Wng,Zhouling Sun, Ynli Liu, Zhenxin Bo, Cuishn Liu
a State Key Laboratory of Hydraulics and Mountain River Engineering, College of Water Resource and Hydropower, Sichuan University, Chengdu 610065, China
b State Key Laboratory of Hydrology–Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China
c Yangtze River Protection and Green Development Research Institute, Nanjing 210098, China
d Research Center for Climate Change of Ministry of Water Resources, Nanjing 210029, China
e School of Water Resources and Hydropower Engineering, Wuhan University, Wuhan 430072, China
Keywords:Meteorological and hydrological forecasting Uncertainty estimation Bayesian model averaging Ensemble prediction Multi-model
ARTICLEINFO Evaluating the impact of multi-source uncertainties in complex forecasting systems is essential to understanding and improving the systems.Previous studies have paid little attention to the influence of multisource uncertainties in complex meteorological and hydrological forecasting systems.In this study, we developed a general ensemble framework based on Bayesian model averaging (BMA) for evaluating the impact of multi-source uncertainties in complex forecast systems.Based on this framework,we used eight numerical weather prediction products from the International Grand Global Ensemble (TIGGE)dataset, four hydrological models with different structures, and 1000 sets of parameters to comprehensively account for the input, structure, and parameter uncertainties.The framework’s application to the Chitan Basin in China revealed that the numerical weather prediction input uncertainty in the forecasting system was more significant than the hydrological model uncertainty.The hydrological model structure uncertainty was more prominent than the parameter uncertainty.The accuracy of the numerical weather prediction dominates the accuracy of the forecast of high flows.In addition, the structures and parameters of the hydrological model and their interactions contributed to the main uncertainty of the low flow forecasts.The streamflow was more realistically represented when the three uncertainty sources were considered jointly.By accounting for the significant uncertainty sources in complex forecast systems,the BMA ensemble forecasting produces more realistic and reliable predictions and reduces the influences of other incomplete considerations.The developed multi-source uncertainty assessment framework improves our understanding of the complex meteorological and hydrological forecasting system.Therefore,the framework is promising for improving the accuracy and reliability of complex forecasting systems.
1.Introduction
The frequent occurrence of natural disasters such as floods and droughts has posed severe challenges to the sustainable development of human society[1].According to the statistics of the Emergency Events Database, from 1989 to 2018, the annual economic losses due to natural disasters worldwide were about 81.4 billion USD, among which floods accounted for 61.9% of all of the natural disaster events and the annual losses due to floods were about 24.52 billion USD.Early and reliable streamflow forecasting is critical for hazard prevention and mitigation, resource allocation, and management decisions [2–4].However, it is difficult to satisfy the needs of efficient water resource utilization and emergency management of extreme events, such as floods and droughts, due to the short streamflow forecasting period based on observational rainfall data [5,6].The forecasting period of the hydrological forecast can be extended by applying meteorological ensemble forecasting information to the forecast and early warning system for hydrology and water resources, which would provide more response time for flood control and disaster mitigation in a basin,further improving our ability to deal with natural disasters and reducing the economic losses and casualties caused by flood disasters [7,8].The uncertainty of a weather forecast is considered by means of integrating the ensemble information, which also provides a reference for the reliable probabilistic hydrological forecast[9,10].In addition, the integration of climate,weather, and hydrological multi-scale forecasts can improve our understanding of the evolution mechanisms of meteorological and hydrological processes,which is also vital to improving the accuracy of hydrological forecasts [11,12].
The complexity and nonlinearity of the meteorological and hydrological system are such that the hydrological model can only simplify the simulation of the complex system.The failure to perfectly describe the physical process inevitably causes many uncertainties,affecting the reliability of the final prediction results[13].Source analysis is an integral part of uncertainty research.Kirkby[14] analyzed the impact of the river network’s topological structure on the watershed hydrology in the 1970s.Kitanidis and Bras[15] summarized the uncertainty sources of conceptual models into the parameters, structure, input of the hydrological models,and initial state of the hydrological system.Krzysztofowicz [16]divided the sources of uncertainty into the model operation,model input, and hydrological model when Bayesian theory is used to realize hydrological probability forecasting.Maskey et al.[17]divided the sources of uncertainty into four categories: the input uncertainty(due to imperfect input information,e.g.,precipitation and evaporation); the parameter uncertainty (e.g., the parameter estimation error); the model uncertainty (e.g., the generalizations and assumptions of the real system); and the natural and operational uncertainty(due to unforeseen causes,e.g.,debris flows,glacier lake overflow, and malfunctioning of system components).Montanari et al.[18]asserted that the uncertainty of the hydrological model system mainly comes from the inherent randomness,model input,parameters,and structure.In general,for hydrological models,it is inappropriate to group the uncertainties of the model structure and parameters together because there is a huge gap in their attributes.Based on previous studies, a consensus has been reached that the input, structure, and parameter uncertainties of the model are the main uncertainties [19], and the additional uncertainties are mainly the arguments about the randomness of the factors, the initial state, and uncontrollable factors, which are difficult to quantify in hydrological forecasting.
Probabilistic forecasts and ensemble forecasts are useful means of quantifying the uncertainty of hydrological forecasting.Considering the sources of uncertainty through ensemble forecasting is an important way to reduce the uncertainty and improve the accuracy and reliability of the forecast.In practical applications, a probabilistic forecast combines the forecasting and management decision processes to assist managers in considering the potential forecast risks in a specific way and to better reflect the value of the meteorological and hydrological forecasts [20–22].Therefore,it is of vital practical significance for meteorological and hydrological forecasts to quantify and reduce the uncertainty through ensemble forecasting and probabilistic forecasting.The current uncertainty analysis methods for hydrological forecasting can be divided into two categories.The first approach is multi-source uncertainty analysis, which quantifies the uncertainties from the different sources, such as the model input, structure, and parameter uncertainties, and it further achieves hydrological probability forecasting considering the multi-source uncertainties using an ensemble method.The most representative method is the Bayesian total error analysis (BATEA) method, proposed by Kavetski et al.[23].It describes the input uncertainty by rainfall multiplier parameters, randomizes the sensitivity parameters of the model,and then applies the Markov chain Monte Carlo method to randomly sample the model parameters and deduce the posterior distribution of the streamflow [24,25].Since the uncertainty of the model structure is not well considered in this method, Ajami et al.[26]developed an integrated Bayesian uncertainty estimator(IBUNE)method based on the BATEA to comprehensively consider the uncertainties of the model input,structure,and parameters,in which the uncertainty of the model structure is estimated using the Bayesian model averaging (BMA) method.Wu et al.[27] used the hierarchical Bayesian method to assimilate the uncertainties of the model,observations,and parameters of the modèle du Génie Rural à 4 paramètres journalier(GR4J)conceptual model,and their results revealed that the estimation precision of extreme events was improved by assimilation of the soil moisture and observed streamflow.Strauch et al.[28] used ensemble precipitation and the BMA method to analyze the impact of the precipitation uncertainty on the parameters and prediction uncertainty of the soil and water assessment tool(SWAT)model.Sun et al.[29]used the BMA method to quantify the influence of the uncertainty of the satellite precipitation input on the hydrological simulation, and their results revealed that the combination of the multi-satellite precipitation ensemble and BMA improved the forecast performance.Yin et al.[30]used the BMA ensemble method to account for the model parameter uncertainty in groundwater modeling,and their results showed that explicitly quantifying the model uncertainty can provide more reliable groundwater level prediction information.
Another method is total error analysis, which quantifies the total uncertainty of the hydrological forecasting according to the forecasting error.The most typical method is the Bayesian forecasting system proposed by Krzysztofowicz [16], which determines the posterior distribution of the forecast streamflow using the linear-normal hypothesis of the likelihood function.In fact,most hydrological processes do not satisfy this hypothesis.In addition, the heteroscedasticity method of residual error models will influence the uncertainty of the streamflow forecast directly [31].There are also differences in the forecast uncertainty at different flow levels.The linear relationship of a high flow is more significant than that of a low flow, and the data for high flows are more concentrated [32].Therefore, Coccia and Todini [33] developed a model condition processor for uncertainty assessment,which uses truncated normal joint distributions to represent the relationship between the forecast and the observed value at different flow levels.Although these methods have good application prospects in real-time flood forecasting due to their high efficiency,they cannot separate the uncertainties from the different sources.
A hydrological forecast is influenced by various factors and has a vast range of uncertainty sources,so the uncertainties such as the input,model structure,and parameters should be considered comprehensively.At present, most studies on uncertainties have been carried out on the input, structure, and parameter uncertainties separately, and few studies have quantified the multi-source uncertainty in hydrometeorological prediction [34–37].In addition, many uncertainty studies were only carried out on the basis of observed rainfall combined with rainfall multipliers [38,39],and research on the uncertainty of meteorological and hydrological forecasting is still lacking [22].In meteorological and hydrological forecasting, both the precipitation forecast and the hydrological model (structure and parameters) have enormous uncertainties,which are the main sources of error in streamflow forecasting.It is valuable to effectively integrate the multi-source uncertainties and to explore the influence of multi-source uncertainties in streamflow forecasting.Such a study can enhance our awareness of the different error sources and their influences on complex meteorological and hydrological forecasting systems.In addition,it can provide a predominant reference for early and reliable streamflow forecasting.Therefore, based on the uncertainties of the model input, structure, and parameters, in this study the control numerical weather prediction (NWP) products of eight countries from the International Grand Global Ensemble (TIGGE)center (i.e., China Meteorological Administration (CMA), Centro de Previsão de Tempo e Estudos Climáticos (CPTEC), Canadian Meteorological Centre (CMC), European Centre for Medium-Range Weather Forecasts (ECMWF), Japan Meteorological Agency(JMA), Korea Meteorological Administration (KMA), the United Kingdom Met Office(UKMO),and National Center for Environmental Prediction(NCEP))were used as the ensemble input.Four structural hydrological models (e.g., the Xin’anjiang (XAJ) model, GR4J model, the simplified version of the hydrology model (SIMHYD),and the variable infiltration capacity (VIC) model) and 1000 optimal parameter sets were combined to carry out meteorological hydrological streamflow forecasting for the Chitan watershed in China, and the analysis of variance (ANOVA) method and the BMA model were used to analyze the uncertainty and influence of the meteorological–hydrological forecast from the perspectives of the model input, parameters, and structure.
The goal of this study was to address three scientific problems.The first was the construction of a comprehensive evaluation framework to reasonably evaluate the multi-source uncertainty in meteorological and hydrological forecasting.The second was determining how to quantify the uncertainties of meteorological and hydrological forecasting from different sources and which uncertainties are more influential.The third was determining the impact of multi-source uncertainty on meteorological and hydrological forecasting and how to reduce it.Section 2 presents the assessment framework for multi-source uncertainties and the case study area.Section 3 summarizes the results and discussion, and Section 4 presents the conclusions of the study.
2.Methodology and study area
Fig.1 presents the assessment framework for the multi-source uncertainties.Since the natural and operational uncertainties are difficult to consider in hydrological forecasting, we mainly focus on the three uncertainty sources of the meteorological input,hydrological model structure, and parameters in a meteorological and hydrological forecasting system.Regarding the input uncertainty, different types of models use different data sources.For example, the lumped model requires information such as precipitation and temperature data, while the distributed model also requires land use and underlying surface information.The error of the input information will have an impact on the model.As precipitation is the most directly influential factor[40],we focused on analyzing the impact of the precipitation forecast ensemble (such as the NWP products provided by the CMA, CPTEC, CMC, ECMWF,JMA, KMA, UKMO, and NCEP).
The uncertainty of the model structure can be viewed from two perspectives: different watershed models (e.g., distributed and lumped models) and different processes in the same model (e.g.,different runoff confluence equations are used in the XAJ model).The former is described by the original model’s architecture, and the difference in the structure is reflected in many aspects,including the modeling principle, modeling method, and subprocess complexity [26].The latter pays more attention to the details of the hydrological processes.Within the same model, different mathematical and physical methods are used to describe the same sub-processes, such as evapotranspiration, infiltration, runoff formation, and routing [41].In order to reflect the difference in the results of the different models, lumped models (e.g., XAJ, GR4J,and SIMHYD) and distributed models (e.g., VIC) are used as model sets.
The parameter uncertainty can be influenced by the parameter estimation algorithm, objective function, and observed discharge error used for the calibration[42,43].Due to the high dimensional nonlinearity of the parameters and the influence of the estimation methods, the concept of the equifinality phenomenon inevitably exists in hydrological models [44].At present, generalized likelihood uncertainty estimation (GLUE) and the Bayesian method are commonly used for parameter uncertainty estimation [45].Since we evaluated the uncertainty from the perspective of the ensemble, we chose GLUE as the parameter uncertainty analysis method and analyzed the impacts of the different parameters using Monte Carlo sampling.

Fig.1.Assessment framework for multi-source uncertainties in meteorological and hydrological forecasting.KGE: Kling–Gupta efficiency; SCE-UA: shuffled complex evolution optimization developed at the University of Arizona; GLUE: generalized likelihood uncertainty estimation; NSE: Nash–Sutcliffe efficiency; RE: relative error.
Finally, we selected eight numerical prediction products, four hydrological models with different structures, and 1000 sets of parameters as the basic set of the three types of uncertainties and used ANOVA and the BMA algorithm to quantitatively analyze the uncertainties of the different ensemble scenarios.In addition, the utility of the ensemble forecast was evaluated from both the deterministic and uncertainty perspectives.
2.1.Hydrological models and parameter optimization
The multi-model set includes the XAJ, GR4J, SIMHYD, and VIC hydrological models, which have different structures.The XAJ,GR4J, and SIMHYD are lumped models, and the average precipitation and evaporation are used as inputs.The XAJ model is mainly composed of three layers (soil evapotranspiration, runoff yield,and runoff separation) and linear reservoir flow routing, which can simulate the three runoff components of surface, subsurface,and groundwater flow [46].In the GR4J model, the runoff yield and flow routing are simulated using nonlinear reservoirs, and the groundwater exchange can also be considered in the simulation.The SIMHYD model contains four components, for example,interception and evaporation loss,soil moisture,runoff separation,and water storage modules[47].It considers two flow yield mechanisms,that is,runoff formation from the natural storage space and runoff formation due to input in excess of the infiltration capacity.In addition, and the lag algorithm is added to consider the flow routing.The VIC model is a large-scale distributed hydrological model, which mainly considers the physical exchange between the atmosphere, vegetation, and soil based on a sub-grid [48].In addition, the sub-grid can also consider the spatial variability of the underlying surface and the precipitation information.In this study, the grid resolution was set as 0.25°, and the grid precipitation, maximum temperature, and minimum temperature data were used as the model inputs.Since the diversity of the models is a key element for including the error in model conceptualization and structure, we included an ensemble of multiple models with four completely different structures, which can maximize the probability of encompassing the most effective way to describe the structural uncertainty [49].
The shuffled complex evolution optimization developed at the University of Arizona (SCE-UA), a global optimization algorithm,was used to optimize the parameters of the four hydrological models uniformly,and the Nash–Sutcliffe efficiency(NSE)and the relative error (RE) were used as the objective function.The SCE-UA algorithm combines the deterministic and stochastic search techniques and the principle of biological competitive evolution, so it can efficiently search for complex problems with high dimensions,nonlinearity, and discontinuity [50].It has been widely used in parameter optimization of hydrological models.We assumed that the algorithm terminates the loop when one of the following two conditions is met: ①The number of iterations reaches 20 000, or②the objective function still cannot improve the accuracy by 0.01% after ten operations.
2.2.Generalized likelihood uncertainty estimation
Generalized likelihood uncertainty estimation is a hydrological simulation uncertainty analysis method proposed by Beven and Binley[44],which was developed based on the regionalized sensitivity analysis (RSA) method.The specific steps of GLUE analysis are as follows:
(1) Determine the likelihood objective function.The likelihood objective function is mainly used to judge the effect of the streamflow simulation.In this study, the NSE and RE was used as the double likelihood objectives.
(2) Sample the parameter set and calculate the likelihood objective function.Usually, the Monte Carlo method is used to sample the parameter set according to the parameter range and prior distribution form,and then,the likelihood objective function is calculated using the model.In this study, the SCE-UA algorithm was used for the parameter optimization.In the optimization process, a series of parameter sets and objective function values involved in the iterative calculation are generated.Therefore, in order to simplify the calculations, we directly took all of the parameter samples and objective function values involved in the SCE-UA algorithm’s iterative calculation as samples in order to omit the sampling steps needed when using the Monte Carlo method.
(3) Select effective parameter sets.The most effective parameter set is identified according to the sample likelihood value and likelihood criteria.In this study, we set NSE >0.7 and RE within±20% as the effective result, and the corresponding parameter set was defined as the effective parameter set.
(4)Analyze the model parameter uncertainty.First,the NSE of the effective parameter set is normalized,and the normalized likelihood value is taken as the probability weight of the parameter set.Then, for each moment, the streamflow simulation values of the effective parameter set are sorted from smallest to largest.Finally,the cumulative probability is calculated using the probability weight of each parameter set,which is taken as the cumulative probability of the simulated flow.Then, the confidence interval of the parameter uncertainty for the simulated flow can be obtained.
In addition, according to the probability weight of the parameter sets,the Monte Carlo method is used to sample 1000 parameter sets from the effective parameter sets as the representative set of the model parameter uncertainty, which is used to analyze the interaction between the model input, structure, and parameters.
2.3.ANOVA approach
The three sources of uncertainty in hydrological forecasting,namely, the eight NWPs, four hydrological models (HMs), and 1000 parameter sets (Pars), were assessed using ANOVA, which has been proposed in hydrological climate-impact projections[51].In three-way ANOVA, the total sum of squares(SST) is calculated using Eq.(1), which can be partitioned into the sum of squares from the model input (SSTNWP), model structure (SSTHM),model parameters (SSTPar), and interaction terms of these three factors (SSTNWP–HM, SSTNWP–Par, SSTHM–Par, and SSTNWP–Par–HM).
2.4.BMA method
BMA is a statistical post-processing method based on Bayesian theory, which can consider the model uncertainty [28,52].It can effectively consider the uncertainty of the models and combine the different information to maximize the integration of the forecast results of the various models.The principle is as follows.

where k=1,2,...,K;p(fk|Y)is the posterior probability of member model fkunder the observed process Y,which reflects the matching between fkand the observed process Y.In fact,p(fk|Y)is the weight wkof the BMA model.pk(Q|fk,Y)is the posterior distribution of the forecast value Q under member model fkand observed process Y.
The forecast values of the BMA model are the weighted average of each member model.Both the member model and the observed process obey a normal distribution.The forecast values of the BMA model are as follows:
where E is the expectations of BMA forecast;g(·)is the Gaussian distribution that is defined by mean fkand variance δk2.
We chose the expectation maximization (EM) algorithm to solve the BMA model [30].The premise of the EM algorithm requires that the data obey a normal distribution, so a Box–Cox transformation should be carried out in the measurement and forecasting process before solving the BMA model [52].The specific solving steps and uncertainty estimation method are shown in Fig.2.
2.5.Evaluation metrics
2.5.1.Deterministic evaluation metrics
We selected three commonly used conventional metrics for the deterministic evaluation:the NSE, root mean square error(RMSE),and water RE.These metrics judge the effect of a deterministic forecast from the perspectives of the streamflow forecast accuracy,process, and total amount, respectively.They are defined as follows:
where Qsim,tand Qobs,tare the simulated and observed streamflow at time t, respectively.n is the length of the series.
2.5.2.Uncertainty evaluation metrics
Xiong et al.[53] defined several metrics for model uncertainty evaluation.In this study, the containing ratio (CR), average bandwidth (B), and average deviation amplitude (D) were selected to evaluate the effect of the uncertainty interval.
CR is defined as the ratio of the observed data contained in the forecast uncertainty interval.The best value for CR is 100%.
B is defined as the average of the upper and lower boundary widths of the uncertainty interval.Under the condition of a high CR, a smaller B value is better.
where qutand qltrepresent the upper bound and lower bound of the uncertainty interval at time t, respectively.
D is a metric for describing the deviation between the center line of the uncertainty interval and the observed hydrograph, and it is defined as follows:
2.6.Study area and data sources
2.6.1.Study area
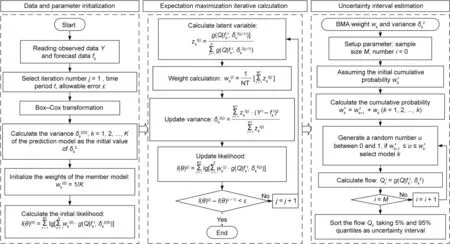
Fig.2.Flow chart of the BMA model and the uncertainty interval estimation.θ represents the BMA parameters wk and δk2.NT is the length of the observation sequence.t represents the sequence of time.
The Chitan Basin was chosen as the study area.It is located in the middle and upper reaches of the Jinxi River system in Fujian Province, China.The basin covers an area of 4766 km2, accounting for 66% of the Jinxi Basin.The Chitan watershed has a subtropical climate, with an average annual precipitation of about 1800 mm,and the total precipitation in the flood season (March to June)accounts for about 62% of the annual precipitation.Therefore, the Chitan Basin is vulnerable to typhoons and heavy rainfall during the flood season.Cold and warm air masses often meet in the Chitan Basin because of its special geographical location, so the daily precipitation often exceeds 50 mm.The annual mean rainstorm(daily precipitation >50 mm) frequency in the basin is about 3.7 times per year, and the frequency had exhibited an increasing trend (Fig.S1 in Appendix A).In addition, the Chitan Basin has a faster flood flow speed and more serious flood disasters because the basin is fan-shaped, and the terrain within the basin is very undulatory [57].Hence, advanced and accurate forecasts of the streamflow in the basin are essential for disaster prevention,early warning, and the coordinated allocation of water and power resources in the Jinxi area.
2.6.2.Forcing data
We used the daily precipitation, evaporation, and streamflow data recorded at stations in the Chitan Basin from 2012 to 2017.There are 18 rainfall stations, one evaporation station and one streamflow station in the basin,at which the evaporation is determined using a D20 evaporator pan.With a height of 10 cm and a diameter of 20 cm,the D20 pan has been widely used in the observation of water surface evaporation[54].For the XAJ,GR4J,and SIMHYD lumped hydrological models,the evaporation of a single gauge is directly used as the substitute value of the evaporation input of the model,while the precipitation at all of the stations is processed into the mean precipitation of the basinusing the arithmetic average.The VIC model also requires maximum and minimum temperature data,and we used the information of a gridded daily observation dataset over China(CN05.1)as a substitute[55].This dataset has a high quality and has been widely used in climate assessment and hydrological modeling in China[56,57].For the simulation of the VIC model,we used the inverse distance weight method to unify the site and grid data into a 0.25°computational grid.
The ensemble precipitation inputs for the hydrological models were retrieved from the TIGGE website.The precipitation control forecast products (i.e., CMA, CPTEC, CMC, ECMWF, JMA, KMA,UKMO, and NCEP) from 2013 to 2017 were selected, which have a ten-day forecast period and a spatial resolution of 0.5°.The Universal Time Coordinate(UTC)00:00 was selected as the starting time of the forecast, which is equal to China standard time 8:00(UTC +8:00).This is exactly consistent with the starting time of China’s daily meteorological observations.The TIGGE site has been providing data to researchers since October 2006 and is now widely used in meteorological and hydrological studies [58,59].At present, there are three TIGGE ensemble database hosted sites across the world, including the NCEP in the United States, the ECMWF in Europe,and the CMA in China,which contain numerical forecast products from 13 member countries and all of the data are provided free of charge.We can download the control forecast data from ECMWF website†† https://apps.ecmwf.int/datasets/data/tigge/levtype=sfc/type=cf/..
3.Results and discussion
3.1.Hydrological simulations
We selected 2012–2017 as the study period,of which 2012 was the warm-up period, 2013–2015 was the calibration period, and 2016–2017 was the verification period.In this study, the NSE was selected as the objective function of the optimal calibration of the four hydrological models, and the SCE-UA algorithm was used to calibrate the hydrological model parameters.In addition,the RE and RMSE between the observed and simulated streamflow were used as the evaluation metrics of the streamflow simulation error.The evaluation results of the streamflow simulation based on the optimal parameter set are presented in Table 1.The results show that the GR4J and XAJ models had higher accuracies and lower errors, and their performances were slightly better than those of the SIMHYD and VIC models in the Chitan Basin.In addition, the scatter density map of the observed and simulated streamflow (Fig.3) shows that there was a good consistency between the simulated and the observed streamflow scatter overall.However, we found that the hydrological models generally underestimated the maximum streamflow on a more microscopic scale, and GR4J and VIC also underestimated the extremely low streamflow.Nevertheless, the comprehensive performance of the four models in the simulation of the streamflow in the Chitan Basin was still excellent, that is, all of the NSE values were greater than 0.8 and the RE values were within ±10% [60].Overall, the results show that these four models can be adapted to meteorological and hydrological coupled forecasting in the Chitan Basin.
Table 1 shows that no one model performed significantly better than other models in all of the periods and aspects because the different models inevitably contain uncertainties due to the generalization of their structures.In addition, the model parameters also exhibited the phenomenon of different parameters with the same effect in the optimization process,and the parameter combinations with NSE of >0.7 and RE within ±20% exceeded 1000 sets.These parameter values were also distributed within the entire value range (Fig.S2 in Appendix A), especially for the SIMHYD and VIC models, which had large parameter uncertainties.Therefore, we further analyze the model parameters and structural uncertainties in the following section.
3.2.Uncertainty from the hydrological model
It should be emphasized that we only discuss the uncertainty of the hydrological model in this section.The uncertainties of the hydrological model mainly included the parameter uncertainty and structure uncertainty.In order to reflect the impact of the parameter and structure uncertainties well,the deterministic input based on the observed precipitation was used to analyze the uncertainties of the parameters and structure of the hydrological model.First, the parameter uncertainty was analyzed using the GLUE method,and the sample library of the parameter set was obtained during the parameter optimization and calibration using the SCEUA algorithm.Then, the parameter set corresponding to the resultwith NSE >0.7 and RE within ±20% of the streamflow simulation results was selected as the effective parameter set, and 1000 sets of parameters were sampled using the Monte Carlo method to analyze the uncertainty of the parameters.In addition,the uncertainty of the structure was analyzed using four hydrological models with different structures (XAJ, GR4J, SIMHYD, and VIC), and the BMA algorithm was used to estimate the uncertainty of the model structure.

Table 1Performance statistics of the different hydrological models during the calibration and verification periods.
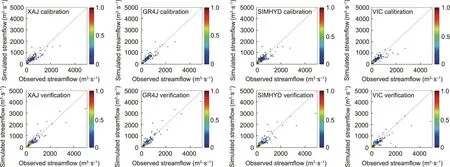
Fig.3.Streamflow simulation of the four hydrological models during the calibration and verification periods.Legend colors represent scatter density.
3.2.1.Uncertainty from hydrological model parameters
The GLUE method was used to analyze the parameter uncertainties of the four hydrological models.In addition, the CR, B,and D values of the uncertainty interval were calculated.Table 2 presents the evaluation results.In terms of CR, those of the VIC and SIMHYD were higher than the others, and that of the GR4J model was lower than the others.Furthermore, from the perspective of the B value, the SIMHYD model had the largest B value, with a greater uncertainty.Moreover, from the perspective of the D value, the SIMHYD and VIC models had the largest deviations, and the GR4J model had the smallest deviation.Overall,the parameter uncertainty of the SIMHYD model was relatively high, and that of the GR4J model was relatively small.The uncertainties of the four hydrological models were significantly lower during the calibration period than during the verification period.However, the superiorities of the different models were different, and no model had obvious advantages in all aspects.This phenomenon is consistent with the results of Clark et al.[61], who analyzed 79 model structures and showed that a single model structure is unlikely to provide the best simulation for all situations.This also demonstrates the necessity of performing ensemble forecasting by combining several model structures[41].
The influence of the model parameter uncertainty on the streamflow simulation was analyzed by comparing the flow duration curves of the observed and simulated streamflow (Fig.4).Fig.4 shows that the parameter uncertainty caused a greater uncertainty for the simulation of extreme floods with a low exceedance probability.In general,the GR4J and SIMHYD models,which consider the parameter uncertainties, estimated the extreme floods better than the XAJ and VIC models, and the parameter uncertainty intervals of these models covered more of the observed extreme floods than other models.However, almost all of the parameter sets failed to estimate the maximum observed flow, which indicates that the hydrological model has a serious underestimation problem regarding extreme floods.Although some underestimation was reduced through parameter optimization, the underestimation of extreme floods was still difficult to balance.For the low flow simulations, the GR4J model and VIC model underestimated the low flow in most of the parameter scenarios.Therefore, although parameter optimization can improve the low flow simulation, the uncertainty of the model structure still has a significant impact on it.
3.2.2.Uncertainty from hydrological model structure
In order to effectively investigate the influence of the uncertainty of the model structure on the streamflow stimulation, the BMAmodel was employed in the ensemble forecasting under the optimal parameters for the four models.Table 2 presents the evaluation results for the 90% uncertainty interval for the hydrological model structures.The results indicate that the CR of the BMA–HM forecast interval exceeded 93.88%, which was significantly higher than the CRs of the four models’ parameter uncertainties (the highest was the VIC model,and the CR was 91.23%during the calibration period).In addition,the B value from the uncertainty of the model structure was slightly higher than that of the four model parameter uncertainties(the highest was the SIMHYD model,the B value during the calibration period was 178.38 m3·s-1).This revealed that the BMA ensemble forecast considering the uncertainty of the model structure had a relatively better quality than the forecast considering the parameter uncertainty,and it obtained a higher interval coverage under the condition of a lower uncertainty at the same time.

Table 2Evaluation results of the 90% uncertainty interval for the hydrological model parameters and structure during the calibration and verification periods.BMA–HM denotes the ensemble forecast of four hydrological models based on the BMA.

Fig.4.Flow duration curve of the observed streamflow and the 90% uncertainty interval for the hydrological model parameters during the calibration and verification periods.The inset plots show the flow duration curve for the low stream flow with a 75.0%–99.9% exceedance probability.

Fig.5.95% confidence intervals for the uncertainty of the hydrological model parameters (for the VIC model) and structures (for the BMA–HM based on the optimal parameters) during 2017.
The streamflow series of the ensemble forecast and the uncertainty interval for 2017 are shown in Fig.5.In addition,the streamflow simulated by the VIC model and its parameter uncertainty interval are also depicted for comparison.We found that the results of the streamflow simulated using the ensemble forecast considering the structural uncertainty performed better than that of the VIC model considering the parameter uncertainty, and it estimated the extreme streamflow better under the close interval bandwidth of the two scenarios.This conclusion is further confirmed by the flow duration curve of the BMA–HM shown in Fig.6, which also reflects the fact that the forecast considering the uncertainty of the model structure improves the underestimation of extreme floods by the hydrological model to a certain extent[62].Further comparison with the GR4J simulation process in Fig.5 revealed that the GR4J model was the best in terms of simulating extreme floods, and the improvement of the peak forecast by considering the uncertainty of the model structure was mainly due to the contribution of the GR4J model.
The above results are all based on analysis of the optimal model parameter set considering the uncertainty of the model structure.In order to obtain a universal analysis, the BMA forecast was carried out independently for each of the 1000 parameter sets while considering the uncertainty of the model structure and then considering the NSE, RE, and RMSE of the final forecast results.Furthermore, the indicators corresponding to the 1000 sets of parameters were used as a set of violin charts (Fig.7).The results indicate that the BMA forecast considering the uncertainty of the model structural was closest to the forecast results of the optimal model among the four models,with a higher NSE and lower RE and RMSE.In addition,the violin plot of the BMA–HM was flatter than those of the other hydrological models, demonstrating that the BMA forecast that only considered the model structural uncertainty also reduced the impact of the hydrological model parameter uncertainty to a certain extent [63].
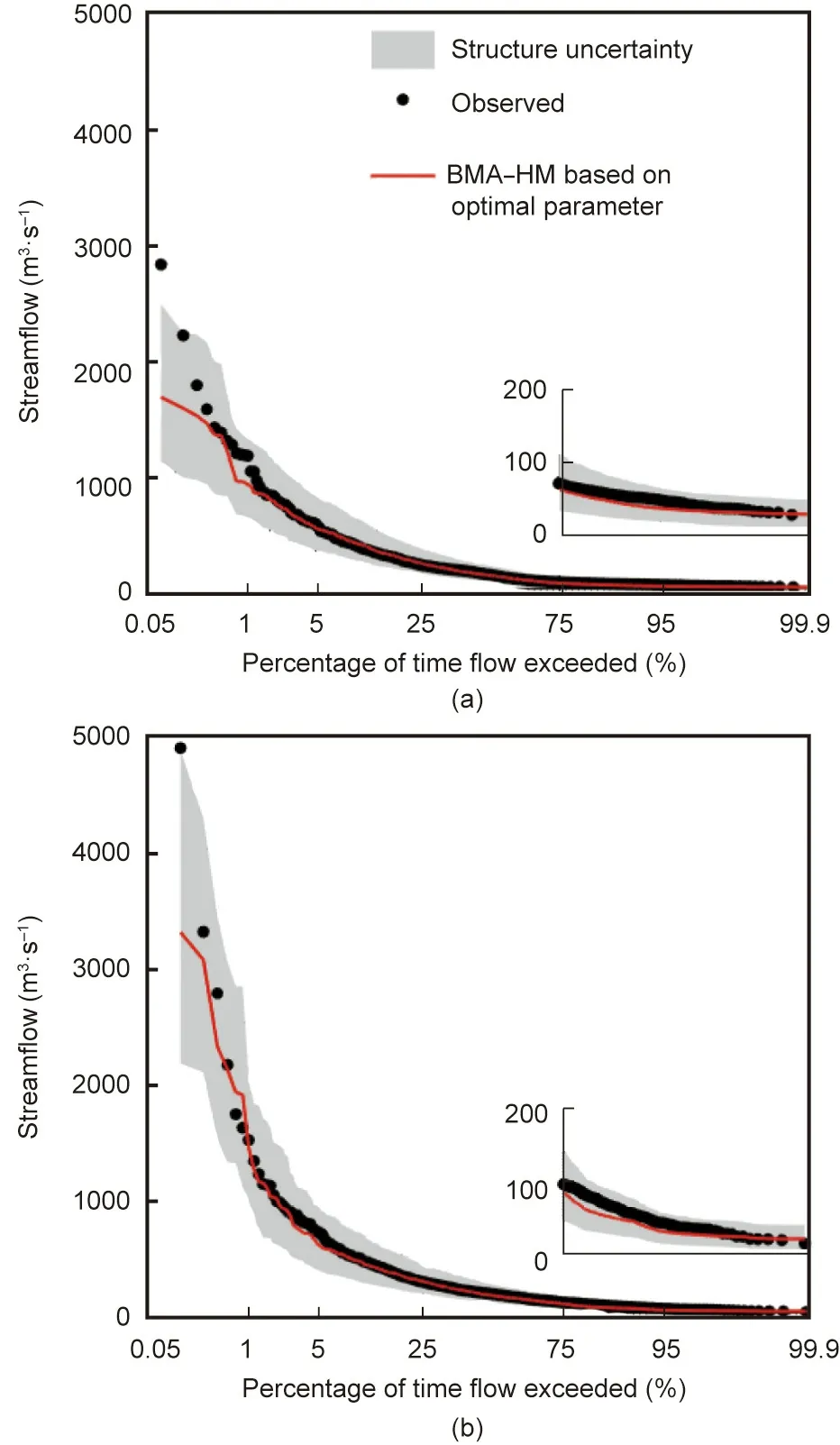
Fig.6.Flow duration curve of the observed streamflow and 90% uncertainty interval for the hydrological model structures.The inset plots show the flow duration curve for the low streamflow with a 75%to 99.9%exceedance probability.(a) BMA–HM calibration; (b) BMA–HM verification.
3.3.Uncertainty from NWP
3.3.1.Meteorological–hydrological coupled streamflow forecasting based on NWPs
The precipitation control forecast products of eight NWPs(CMA,CPTEC,CMC,ECMWF,JMA,KMA,UKMO,and NCEP)obtained from the TIGGE website were used as the input of the calibrated hydrological models(XAJ,GR4J,SIMHYD,and VIC).The input variables of the model,except for precipitation,remained unchanged.Taking a lead-time of 1–4 days as an example,the NSE,RE,and RMSE for the streamflow under different coupled forecast scenarios during the calibration and verification periods were calculated.Then, the evaluation metrics of the forecast results of the different hydrological models based on the same NWP product were visualized as a set of box plots (Fig.8).
The NSE,RE,and RMSE of the streamflow forecast results shown in Fig.8 indicate that when the hydrological model was coupled with the NCEP and ECMWF, it performed better in terms of the streamflow forecast than when it was coupled with other NWP products, and the performance of the coupled CPTEC model was the worst.These results are consistent with the results of Shu et al.[57], who evaluated the applicability of these eight NWP products in Chinese mainland and reported that the ECMWF and NCEP has a more robust performance in precipitation forecasting,while the CPTEC had a poorer performance and the JMA underestimated the heavy rainfall events.As the lead time increased, the forecasting ability of each model decreased significantly.Among them, the streamflow forecasting ability of the coupled CPTEC and CMC models decreased rapidly with a relatively large decline,while the performance of the coupled JMA model exhibited a smaller change in 1–4 days in future compared to the other models.
By further analyzing the differences between the performances of the different hydrological models in streamflow forecasting, it was found that the VIC model and the SIMHYD model performed better than the XAJ model and the GR4J model in most of the scenarios.Although the GR4J model and the XAJ model were effective in terms of the streamflow simulation based on the observed precipitation,this does not mean that they were also advantageous in terms of meteorological and hydrological coupled streamflow forecasting, which may be related to the parameter uncertainty, the model error, and the complexity of the model structure.In addition,the forecast abilities of the different hydrological models varied with the lead time, indicating that when the streamflow forecast for a one-day lead time was carried out, the differences between the forecast performances of the four hydrological models under the same NWP product was not obvious.However, the differences between the models expanded significantly as the lead time increased, especially when coupled with the CPTEC, CMC,and CMA models.When coupled with the JMA model, this difference had the smallest change compared to the other models.In summary,the precipitation input had a crucial effect on the hydrological forecasting.Tuo et al.[64]pointed out that the uncertainties in hydrological simulations driven by different NWP products propagate to processes such as erosion and contaminant transport,and this will likely result in uncertainty in watershed water management.Therefore, the uncertainty caused by the precipitation input must be considered in complex forecast systems.

Fig.7.Violin charts of the NSE,RE,and RMSE of the four hydrological models and the BMA ensemble forecast.The violin diagram consists of 1000 sets of evaluation indicators corresponding to the model parameters.(a) Calibration; (b) verification.
3.3.2.Ensemble forecast accounting for the uncertainty from the NWP input
Under the four hydrological models and fixed parameter sets,the BMA algorithm was used to ensemble forecast the streamflow process of the coupled eight numerical forecast products.In addition, the deterministic and uncertainty metrics (NSE, RE, RMSE,CR,B,and D)of the streamflow series in the next ten days predicted by the 1000 sets of parameters were calculated.The forecasted streamflow during the calibration period is illustrated in Fig.9.Each box plot in the figure is composed of 1000 sets of forecast metrics for the model parameters.
In terms of the deterministic evaluation of the forecast,the NSE of the streamflow forecast results obtained using the various models is depicted in Fig.9.Fig.9 shows that the box plot of the SIMHYD model was the longest,followed by the XAJ model,which indicates that the parameter uncertainty had a greater impact on these models.In addition, the forecast performances of the four hydrological models decreased with increasing lead time.In general, it can be concluded that the ensemble forecast considering the uncertainty of the NWP input significantly improved the accuracy of the future streamflow forecasting compared with the single-process forecast results (Fig.8).
Specifically,the variation in the RE in Fig.9 shows that most of the relative error was still less than zero despite the greater impact of the parameter uncertainty,and the amount of water was generally underestimated.In addition, the flow duration curve of the streamflow series (Fig.10) indicates that the coupled forecast also universally underestimated the extremely high flows.For the simulation of the low flows,the underestimation of the low flows was obvious when coupled with the VIC model.Further comparison with the RE of the single-process forecast (Fig.8) revealed that the streamflow forecasted by most of the NWP products was also severely underestimated, which indicates that most of the models in the ensemble forecasting underestimated the streamflow.This general underestimation phenomenon was not significantly improved in the BMA ensemble forecast considering the input uncertainty.Consequently, in terms of the NSE and RMSE, the ensemble forecasting effect based on the VIC model was better,but it seriously underestimated the streamflow,which was closely related to the underestimation of the numerical forecast products(Fig.8) and the calibration results of the VIC model itself (Fig.4).
From the perspective of the evaluation of the forecast uncertainty, as the lead time increased, the CR value of the uncertainty interval for the four models slightly decreased (Fig.9).For a oneday lead time, the GR4J model had the highest CR, while the VIC model had the highest CR for the other lead times.Notably, the B and D values of all of the models gradually increased with increasing lead time, and the uncertainty also increased significantly.Among them, the average bandwidth of the SIMHYD model was relatively low, and the uncertainty was also low.In summary,the ensemble forecasts had a higher CR at low flows, but the coverage of the high flows was obviously insufficient based on the relatively large forecasting uncertainty.Although the different hydrological models and parameter combinations reduced some of the underestimations, the large input error of the NWP led to greater uncertainty in the final streamflow forecast results.
3.4.A triple-ensemble forecast accounting for the uncertainties from the model structure, parameters, and inputs
In this section, eight NWP products, four hydrological models,and 1000 sets of parameters were chosen.Then, the BMA method was used for the ensemble forecasting based on 8×4×1000 types of streamflow series.When considering the model input,structure,and parameter uncertainty scenarios, the accuracy evaluation metrics (NSE, RE, and RMSE) and uncertainty evaluation metrics(CR, B, and D) of the forecasting streamflow in the next ten days were calculated.The results are shown in Fig.11.
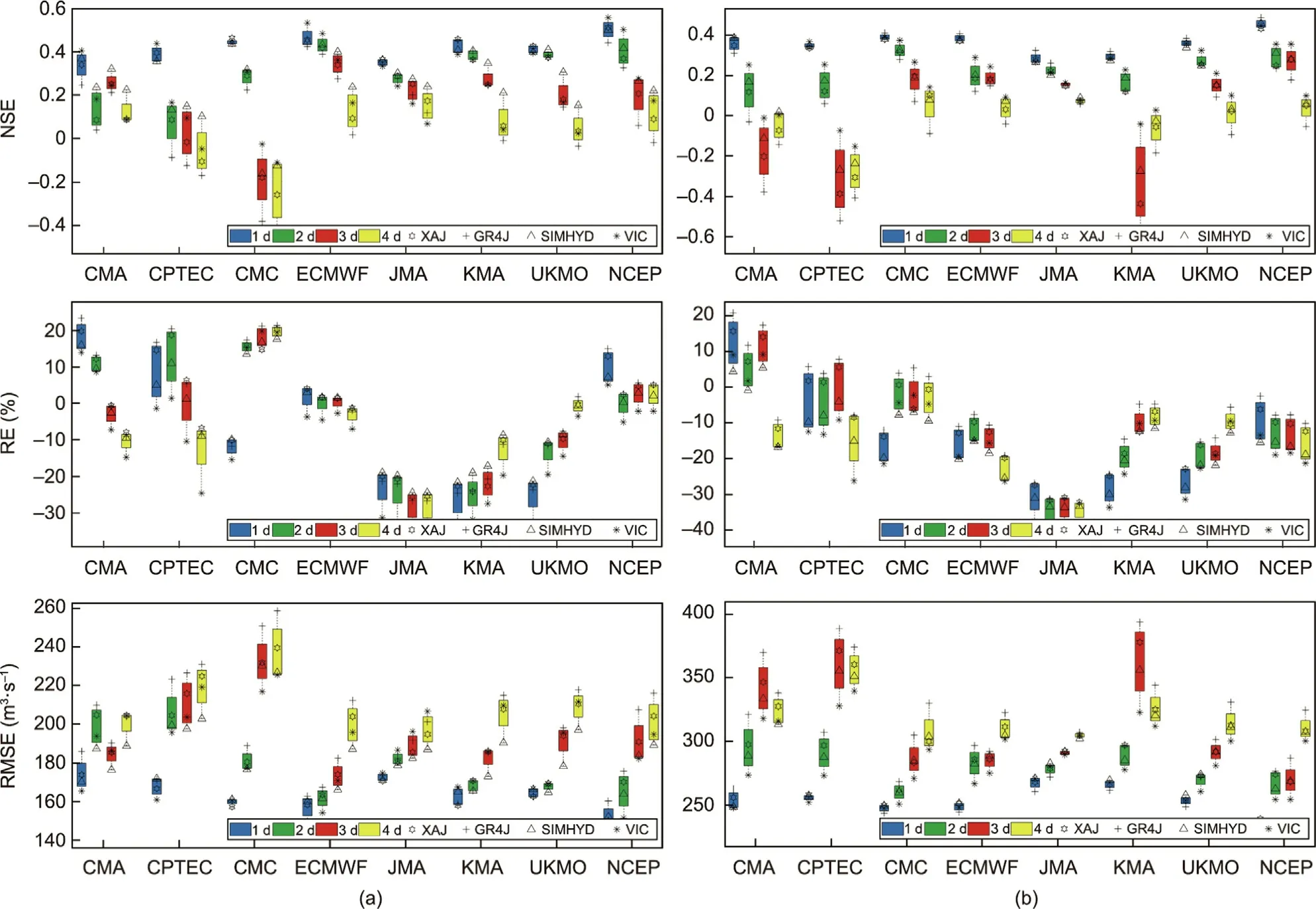
Fig.8.Accuracy of the streamflow forecast coupled with different numerical products during the(a)calibration and(b)verification periods for various lead times(1,2,3,and 4 days).

Fig.9.(a)Deterministic and(b)uncertainty assessment of the BMA ensemble forecasting considering the NWP input uncertainty for the four hydrological models during the calibration periods for various lead times (1, 2, 3, and 4 days).

Fig.10.Flow duration curve of the observed streamflow and 90% uncertainty interval for the NWP input with a one-day lead time.The inset plots show the flow duration curve for the low streamflow with a 75%–99.9% exceedance probability.
In terms of the deterministic evaluation of the streamflow forecasts, for 1- to 4-day lead times, the NSE values of the BMA ensemble forecasts considering the uncertainties of the input, structure, and parameters were all greater than 0.1, and they were better during the calibration period than during the verification period.Nevertheless, the performance of the BMA ensemble forecast decreased rapidly with increasing lead time.The NSE ranged from 0 to 0.2 in the next 6–10 days, and the forecast accuracy slowly decreased.Compared with the forecast results of the single-model without considering any uncertainty(single coupling; Fig.8), the ensemble forecast considering the NWP input and the uncertainty of the hydrological model obviously improved the forecasting accuracy of the streamflow in the next 1–10 days.In particular, in the long-term forecast period after the next four days, the NSE of the ensemble forecast was greater than 0, so it effectively improved the forecast quality of the streamflow.
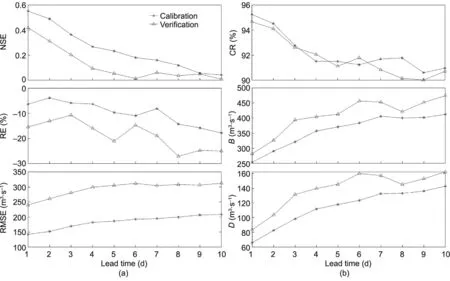
Fig.11.(a) Deterministic and (b) uncertainty assessment of the BMA triple-ensemble forecast accounting for the NWP input, model structure, and parameter uncertainties during the calibration and verification periods for various lead times (1–10 days).
Similarly, from the perspective of the RE of the water volume over the streamflow forecast, the RE values of the ensemble forecasts were all less than zero;the RE gradually became increasingly negative with increasing lead time; and the underestimation phenomenon became more and more serious.Furthermore, based on the RMSE of the streamflow forecast, the forecast error gradually increased with increasing lead time.In addition, compared with the forecast results for the single-model without considering any uncertainty (single coupling; Fig.8), the RMSEs of the ensemble forecasts considering the NWP input and the hydrological model uncertainty were reduced by approximately 20–60 m3·s-1for each lead time, and thus, the quality of the streamflow forecast was effectively improved.
In terms of the uncertainty evaluation of the forecast, from the perspective of the CR,in the next 1–4 days,the CRs of the ensemble forecasts mostly fluctuated between 91.5% and 96.0%, and the coverage rate rapidly decreased with increasing lead time.After the next five days, the CR fluctuated between 90% and 92% during the calibration period, and the coverage rate of the uncertainty interval decreased slowly with increasing lead time.Based on the B and D values of the streamflow forecast, both deviation and D gradually increased with increasing lead time,and the uncertainty also increased significantly.In general,it can be seen from the flow duration curve of the streamflow forecasting process(Fig.12)that the ensemble forecast had a higher CR at low flows.However, the coverage of the high flow was obviously insufficient,and the interval width of the high flow part was evidently larger, so the forecasting uncertainty was relatively large.
3.5.Quantifying and reducing the uncertainties of the hydrological forecast
3.5.1.Contributions of NWP, structure, and parameters to the uncertainty of the hydrological forecast
In order to efficiently quantify and compare the different uncertainty sources, ANOVA was conducted to describe the proportions of the different uncertainty sources and reveal the main uncertainty components of the meteorological and hydrological forecasting system [51].The variance proportions of the different scenarios in the different streamflow quantiles based on a threeway ANOVA are shown in Fig.13.
Fig.13 shows that the contributions of the different uncertainty sources to the total ensemble uncertainty change considerably from the low quantiles to the high quantiles during the calibration and verification periods.In the low quantiles below 35%, the NWP is the dominant source, accounting for about 80% of the total uncertainty during the calibration and verification.In the high quantiles above 85%, the HM and Par are the main contribution sources, followed by their interaction HM–Par.The structural uncertainty of the hydrological model had a significant effect on the low flow (Figs.4 and 10).Therefore,the ensemble forecast accounting for the structural uncertainty had an obvious improvement effect on the low flow forecasting(Figs.6 and 12).In general, as the quantile increases, the influence of the NWP gradually decreases, and the influence of the hydrological model gradually increases.This phenomenon means that the accuracy of the NWP plays a key role in the prediction of the high flow, while the hydrological model mainly dominates the prediction of the low flow.
3.5.2.Accounting for uncertainties from multiple sources simultaneously using ensemble forecasting
Based on the above analysis, the performance of the meteorological and hydrological ensemble forecasting considering the different uncertainty sources is further summarized in this section.The B and D values of the uncertainty interval were used as the uncertainty indicators to quantitatively evaluate the performance of the ensemble forecast, and the results are presented in Fig.14.In addition, in order to better analyze the interactions between the different uncertainty sources,the results of the dual and triple source ensemble forecasts, such as HM–Par, NWP–HM, NWP–Par,and NWP–Par–HM, were further calculated.
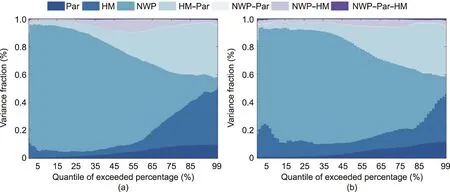
Fig.13.Variance decomposition of the uncertainties in the different streamflow quantiles for a one-day lead time.(a)Calibration;(b)verification.The uncertainty sources are the Par, HM,NWP,HM–Par,NWP–Par, NWP–HM,and NWP–Par–HM.The joint effects are considered for four sets of scenarios, namely, HM–Par(parameter and structure),NWP–HM (input and structure), NWP–Par (input and parameter), and NWP–Par–HM (input, parameter, and structure).
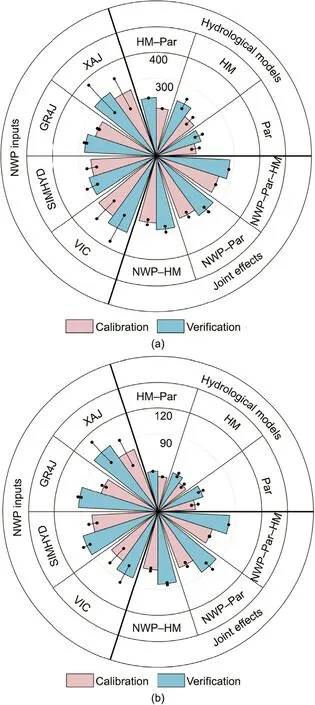
Fig.14.Quantitative assessment of the uncertainty intervals from the different sources during the calibration and verification periods.(a) Average band-width B(m3·s-1);(b)average deviation amplitude D(m3·s-1).The column length represents the mean value of the dataset,and the line represents the standard deviation of the dataset, where the dataset consists of the set result estimates from the other uncertainty sources.
Under the observed precipitation conditions,the B value during the verification period when only considers the model parameter uncertainty was 183.2 m3·s-1, and the standard deviation of the estimated results of the four hydrological models was 15.6 m3·s-1(Fig.14).Among them, the parameter uncertainty of the SIMHYD model was the largest (Table 2), and the uncertainty was significantly greater during the verification period than during the calibration period.Moreover, the uncertainty bandwidth during the verification period was 230.1 m3·s-1when only considering the uncertainty is the model structure,and the standard deviation of the 1000 sets of parameter estimation results was 20.6 m3·s-1.In addition,when considering the uncertainties of the model structure and parameters,the bandwidth of the verification period was 227 m3·s-1, and the average deviation amplitude was 47.4 m3·s-1,which were both smaller than those of the HM and Par scenarios.Thus, it can be concluded that the uncertainty of the model structure was greater than the uncertainty of the parameters, and the BMA ensemble forecasting that considered both the structure and the parameter uncertainties performed better than that which only considered the parameter uncertainty.Poulin et al.[65]reported that the uncertainty in the model structure is more significant than the parameter uncertainty and provides more diverse information.Therefore,hydrological models with different levels of complexity and multiple sets of parameters should be considered to quantify and reduce the uncertainty of the hydrological simulation.
Under the conditions of the precipitation forecast, when only the uncertainty of the NWP inputs was considered, the interval bandwidth of the forecasted streamflow for a one-day lead time during the verification period was 271.6–316.2 m3·s-1, the standard deviation of the 1000 sets of parameters and the four hydrological model estimation results was 5.1–71.9 m3·s-1(Fig.14).In addition, the bandwidth of the forecast uncertainty gradually increased with increasing lead time (Fig.9).Moreover, through comparison of the single-source uncertainty of the model input,parameters, and structure,it was found that the input uncertainty of the NWP products significantly influenced the meteorological and hydrological coupled forecasting process (Figs.13 and 14),and the quality of the NWP products directly determined the accuracy of the final streamflow forecast [66,67].Dahri et al.[48] also pointed out that improving the meteorological input is fundamentally necessary for accurate hydrometeorological analysis.In addition, the uncertainty of the model input evidently increases with increasing lead time,while the multi-input BMA ensemble forecast can obviously improve the accuracy and reliability of the streamflow forecasting [57,68].
By comparing the results of the joint effects of the multi-source uncertainties,it was determined that the bandwidth when considering the input and structural uncertainties during the verification period was(284.4±11.7)m3·s-1,while it was(282.3±12.3)m3·s-1when considering the input and parameter uncertainty.These two values were slightly smaller than when the model input uncertainty was considered separately.This indicates that the model input uncertainty occupied a larger proportion of the entire model chain,and that increasing the ensemble of the structure or parameter uncertainty could further reduce the forecast uncertainty.When considering the model input, parameter, and structural uncertainties at the same time, the interval bandwidth of the ensemble forecast during the verification period was 285 m3·s-1,which was smaller than the highest interval bandwidth when a single source (input) and dual source (input + structure, input +parameter) were considered.Therefore, these results indicate that the BMA ensemble forecast that considers the uncertainty of the entire process can further reduce the effect of not fully considering the other sources of uncertainty compared to the ensemble forecast that only considers a single source or dual sources.
Based on the deviation amplitudes and accuracies of the ensemble forecasts, the accuracies of the single-model, single-source ensemble, dual-source ensemble, and three-source ensemble streamflow forecasts were further compared.We found that the BMA ensemble forecasts that considered the uncertainty improved the accuracy of the future streamflow forecasts more than the single-model forecasts did.Compared with the single-source ensemble forecast (only the input uncertainty was considered),the standard deviation of the deviation amplitude during the calibration period of the dual-source NWP–HM and NWP–Par scenarios were 1.8 and 2.6 m3·s-1, respectively.While in the singlesource ensemble forecast that only considered the input uncertainty, the model parameter and structure had a greater impact,and the standard deviation of the average deviation amplitude during the calibration period was 2.5–16.3 m3·s-1.Thus,it can be concluded that the influences of the other sources in the single source process was reduced by considering the uncertainty of the dual sources, and the credibility of the streamflow forecast was further improved.This conclusion is similar to the findings of Yen et al.[60], who analyzed multi-source uncertainties in watershed modeling and showed that the calibration can be improved by considering the uncertainties from all of the possible sources in complex and large-scale watershed simulations.
However, for the dual-source ensemble forecast that considered the input and parameter uncertainties, the impact of the model structure reached 0.1 NSE in the next three days, and the impact was also greater than that of the dual-source ensemble forecast that considered the input and structure uncertainties(the impact of the parameter was approximately equivalent to 0.05 NSE).In summary, by comprehensively analyzing the accuracy and reliability of the final streamflow forecast,it can be concluded that the performance rankings of the multiple combination scenarios are as follows: the ensemble forecasts that consider the input and hydrological model(structure + parameter) uncertainties; the ensemble forecasts that consider the input and structure uncertainties;the ensemble forecasts that consider the input and parameter uncertainties;the ensemble forecasts that consider the input uncertainty; and the single-model forecasts.
4.Summary and conclusions
Understanding the multi-source uncertainty of the meteorological and hydrological forecast chain is the basis for providing accurate and reliable forecast information, which can better guide hydrological operational forecasts.In this study, a comprehensive multi-source uncertainty assessment framework based on Bayesian model averaging was developed.In its practical application to the Chitan watershed in China, which is prone to floods,we carried out meteorological and hydrological coupled streamflow forecasts using combinations of eight NWP products (CMA,CPTEC,CMC,ECMWF,JMA,KMA,UKMO,and NCEP)from the TIGGE dataset, four hydrological models, and 1000 sets of parameters.In addition, the uncertainty and its influence on the complex prediction systems were investigated from the perspectives of the model input, parameter, and structure.
We found that the XAJ model and GR4J model had better comprehensive performances in the hydrological simulations, while the SIMHYD model and VIC model had greater parameter uncertainties.However, the use of a variety of evaluation metrics revealed that the hydrological models with different structures had different performances in simulating streamflow series, and no one model had obvious advantages in all of the periods and aspects.The four hydrological models selected reproduced the streamflow series in the Chitan Basin reasonably well, which indicates that they can be applied to meteorological and hydrological coupled forecasting.
In the meteorological and hydrological coupled streamflow forecasting, we found that the streamflow forecast performance based on the different NWP models was consistent with the precipitation forecasting effect.For example, when the hydrological models were coupled with the NCEP and ECMWF, the effect of the streamflow forecasting was significantly better than those of the other scenarios.The streamflow forecast coupled with the CPTEC model had a poor effect due to its poor precipitation forecast performance.When coupled with the JMA model, which seriously underestimates heavy rain events, the deviation of the underestimation of the streamflow forecasts was also larger.Moreover, the accuracy of the meteorological and hydrological coupled streamflow forecasts decreased gradually with increasing lead time,while the error increased gradually, but the relative error did not significantly change.
The uncertainty of the model input in the meteorological and hydrological ensemble forecasting was obviously greater than the uncertainty of the hydrological model, and the quality of the NWP forecast basically determined the accuracy of the high-flow forecast.Regarding the structural and parameter uncertainties of the hydrological model, the structural uncertainty was slightly greater than the parameter uncertainty.The structures and parameters of the hydrological model and their interactions contributed to the main uncertainty of the low flow forecasts.BMA ensemble forecasting considering the uncertainty of the model structure estimated the hydrological model’s uncertainty better under the condition of the deterministic input,and it reduce the influence of the parameter uncertainty.Moreover,the BMA ensemble forecast considering the multi-source uncertainty improved the accuracy and reliability of the streamflow forecasts more compared with the streamflow forecast considering a single source or a single model scenario.In general, the comprehensive performances of the various scenarios were as follows:the ensemble forecasts that considered the input and hydrological model (structure + parameter)uncertainties; the ensemble forecasts that considered the input and structure uncertainties; the ensemble forecasts that considered the input and parameter uncertainties; the ensemble forecasts that considered the input uncertainty; and the single-model forecasts.
The preprocessing and post-processing steps of a meteorological and hydrological forecast system are important to improving the streamflow forecast [69].The results of this study show that the uncertainty of the precipitation forecast in the meteorological and hydrological system is significantly greater than the other uncertainties, which also indicates that we need to prioritize the selection of the preprocessing solutions to reduce the input errors in order to more efficiently improve the quality of the streamflow forecasts.However, this does not mean that the improvement of the streamflow forecasting performance only requires the efforts of meteorologists.We also found that the structure and parameters of the hydrological model and their interaction are critical for low flow forecasts, and the hydrological model with a better performance in streamflow simulation may not perform well in meteorological and hydrological forecasting.There may be an offset or superposition effect between the precipitation forecast error and the hydrological model error, which will increase the uncertainty of the prediction results.However, it is clear that when coupled to a better hydrological model, the standard deviation caused by the other factors will be smaller.That is,a hydrological model with a poorer performance will increase the uncertainty of a complex system.Therefore, the post-processing of hydrological forecasts is particularly important in the entire complex system, which also indicates that the improvement and optimization of meteorological and hydrological models is also an essential step in improving the forecasting ability of complex systems.Sharma et al.[70]reported that preprocessing and post-processing can reduce the forecast error in two aspects, that is, reducing the input errors and controlling the output errors, and the coexistence of the two schemes can maximize the accuracy and reliability of the meteorological and hydrological forecast.
Another challenge is the improvement of the prediction model of extreme processes from a model optimization and statistical processing perspective.We found that most of the NWP models underestimated extreme storms, which led to serious underestimation of the streamflow forecasts.Although our ensemble framework improves the underestimation to a certain extent, the effect is still not significant.This is due to the insufficient consideration of the physical processes in the meteorological and hydrological models.It is also related to the deficiencies of the postprocessing methods, such as the ensemble averaging method,which may neutralize extreme values.Therefore,the improvement of a complex system to predict extreme processes requires the joint effort of meteorologists and hydrologists.However, current statistical treatment schemes are mostly based on the overall sequence, which also proves that incorporating conventional preprocessing and post-processing schemes can add additional uncertainties to complex systems [43,69].Therefore, we also need to fully determine the effects of the processing schemes on complex systems and develop more appropriate processing schemes for typical processes in order to better improve the accuracy and reliability of meteorological and hydrological systems in predicting extreme events [33].
Acknowledgments
We gratefully acknowledge the funding provided by the National Key Research and Development Program of China(2021YFC3200201), the National Natural Science Foundation of China (52121006, U2240203, and 51779144), the Second Tibetan Plateau Scientific Expedition and Research (2019QZKK0203), the Fundamental Research Funds for the Central Universities of China(B210204015 and B210204014), and the Consulting Research Project of Chinese Academy of Engineering (2020-ZD-20 and 2021-ZD-CQ-2).
Compliance with ethical guidelines
Zhangkang Shu, Jianyun Zhang, Lin Wang, Junliang Jin, Ningbo Cu, Guoqing Wang, Zhouliang Sun, Yanli Liu, Zhenxin Bao, and Cuishan Liu declare that they have no conflicts of interest or financial conflicts to disclose.
Appendix A.Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.eng.2022.06.007.
- Engineering的其它文章
- Dynamic Deformation Measurement of an Intact Single Cell via Microfluidic Chip with Integrated Liquid Exchange
- The Rational Design and Development of Microalgae-Based Biohybrid Materials for Biomedical Applications
- DART Mission Shows Potential for Planetary Defense by Smashing Asteroid into New Orbit
- Electric Racers Hit the Track, but Still Catching Up
- Micro-Cantilever Electric Field Sensor Driven by Electrostatic Force
- Theory and Practice of Hydrodynamic Reconstruction in Plain River Networks

