基于高频注入的带式输送机SPMSM无传感器控制研究

杨京东,李大伟,杜贤弈,吴 康,任丽霜

(山西大同大学 煤炭工程学院,山西 大同 037003)

矿用带式输送机因其可长距离、连续性地运输大量矿用物料等优点被广泛应用于煤矿井下,目前主要采用异步电机+减速机的驱动方式,但是异步电机的能量转化率低,可调速性不好,大大增加了应用成本[1-2]。PMSM相比异步电机易于实现多极调速,电机轴直接与带式输送机的滚筒相连,提高效率的同时使得系统复杂度减小、维护难度降低,减少了系统的故障点,总损耗可降低40%～60%.

PMSM根据转子结构可分为表贴式永磁同步电机(SPMSM)和内置式永磁同步电机(IPMSM)。由于带式输送机的主滚筒直接嵌套在永磁电动机的外转子上,组成带式输送机直驱型滚筒。这种结构可以简化传动机构,提高传动效率和可靠性,同时,由于外转子直径大,增大了刹车半径,减小了刹车力,从而可提高刹车的可靠性[3]。因此具有外转子结构的SPMSM更适用于带式输送机系统。

由于煤矿井下环境复杂,需要采用无速度传感器控制算法获取转子位置和速度信息。在矿用带式输送机中高速运行时,一般的检测方法通常能够保证控制精度,但当带式输送机低速运行时,SPMSM有用信号的信噪比较低,提取转子信息困难,导致带式输送机不能安全稳定的运行[4]。为保障带式输送机低速稳定运行,采用高频注入法进行低速区间无速度传感器控制。

高频注入法通常有两种:脉振高频注入法和旋转高频注入法。由于SPMSM的凸极率极小,通常适用于脉振高频注入法[5]。脉振高频注入法即在d轴上注入基于高频注入电压幅值Umh和频率ωh的高频余弦电压信号Umhcos(ωht),使SPMSM转子凸极磁场饱和,且SPMSM的参数变化对脉振高频注入法的影响很小,因此在零低速时可以准确地从q轴分量中获得转子的位置信息。

1 三相PMSM的基本数学模型

SPMSM的物理模型如图1所示。

图中ABC为自然坐标系;α-β为静止坐标系;d-q为同步旋转坐标系;ωe为转动速度,vad/s;θ为转动角度,°;N和S表示SPMSM的永磁体磁极;UVW和XYZ分别为三相绕组的首端和尾端。

为使方案更易分析,要假定下列几种情况[6]:

1) 不计电机磁饱和;

2) 忽略电机磁滞损耗;

3) 转子无阻尼绕组。

根据坐标变换理论原理,运用Clark和Park变换可得:

1) 变换的电压方程:

(1)

2) 变换的磁链方程:

(2)

3) 变换的电磁转矩方程:

(3)

式中:pn为磁极数;ψf为永磁体磁链;iq、id为定子电流的交直轴分量;Lq、Ld为定子电感的交直轴分量。

对于SPMSM满足Ld=Lq,公式(3)可简化为:

(4)

式中:pn和ψf均为常数,即iq与Te呈线性的数学关系,可通过iq直接控制Te.

2 脉振高频注入法原理

要对SPMSM进行精准高频注入控制,首先需建立如图2所示的坐标空间位置关系。

定义实际转子与估计转子的夹角为估计误差:

(5)

根据图2,可得转换矩阵为:

(6)

再由公式(1)和式(2)得:

(7)

由于注入SPMSM的信号频率远大于式(7)中的电机角频率,所以SPMSM近似于R-L负载,即:

(8)

式中:p为微分算子;udh、Rdh、Ldh和idh分别为d轴在高频注入时的注入电压量、电阻、电感和电流响应;q轴同理。注入高频信号后可得:

(9)

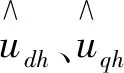
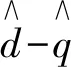
(10)

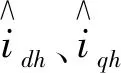
(11)

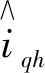
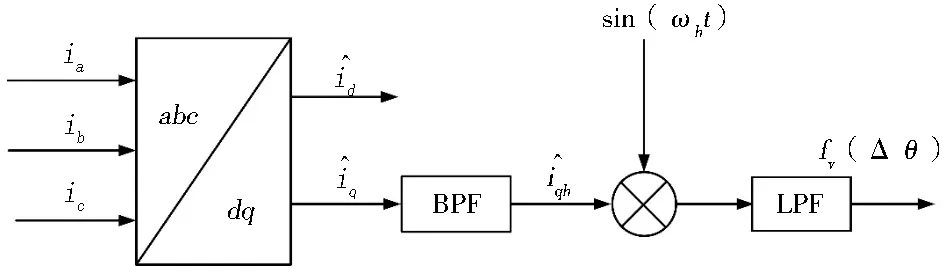
图3 提取估计误差

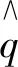
(12)

其中:

(13)

图4为提取估计误差信号后进行转子估算的过程,即通过位置跟踪观测器直接输出转子电角度,对其积分后得出转子估算信息。

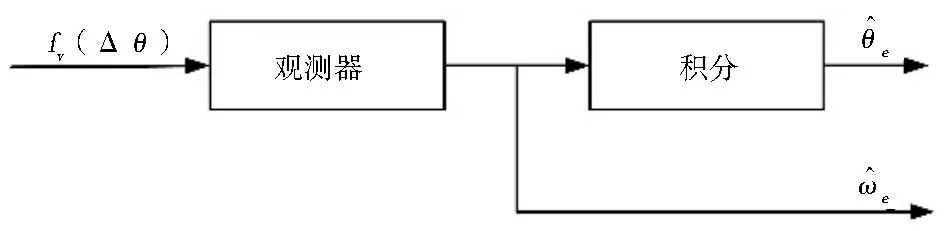
图4 转子估算

3 注入频率和观测器的设计

3.1 选择注入频率

选择注入信号频率时,若频率太高,则因信噪比低导致高频附加噪声大;若频率太低,则LPF带宽降低,电流环带宽也相应降低,影响系统稳定性[7]。

由于负反馈系统要求kv>0,且此时SPMSM近似于R-L负载,则在高频电压激励下,满足0 <ψd<ψq<π/2.综上,在考虑一定余量的情况下,使π/4<ψd<ψq<π/2,即d-q轴的阻抗为ωhLq>ωhLd>R,此时高频注入信号的最低频率为:

(14)

注入频率还需保证在信号提取时能与电机的基波频率相分离,因此需要计算允许的最高频率。在以上最低频率和允许的最高频率范围内取值,才能保证电机的观测器高性能控制。一般在工程中,对高频注入法中的注入频率取值是根据逆变器的开关频率决定的[8],考虑到逆变器中的六个功率开关管频繁切换以及PWM调制技术等因素,高频注入信号的最高频率要小于功率管切换频率的1/6,结合公式(14)可得高频注入信号的频率范围为:

(15)

式中:fs为逆变器在工作过程中功率管的切换频率。

(16)

式中:Ibase为基波电流。

根据式(15)和式(16)给出的注入信号频率和幅值选取范围,选择高频信号的频率为1 kHz,选择信号幅值为80 V.

3.2 设计龙伯格观测器

龙伯格状态观测器为全阶观测器,通过输入变量u及输出变量y对无法直接测量的状态重构以实现对系统状态的观测。对基于电磁角速度和角度的电机状态方程分析可以设计龙伯格状态观测器如下:

(17)

(18)

因此,基于SPMSM速度观测的龙伯格状态观测器结构框图如图5所示。由图5可知,龙伯格状态观测器的精度由式(19)所描述:

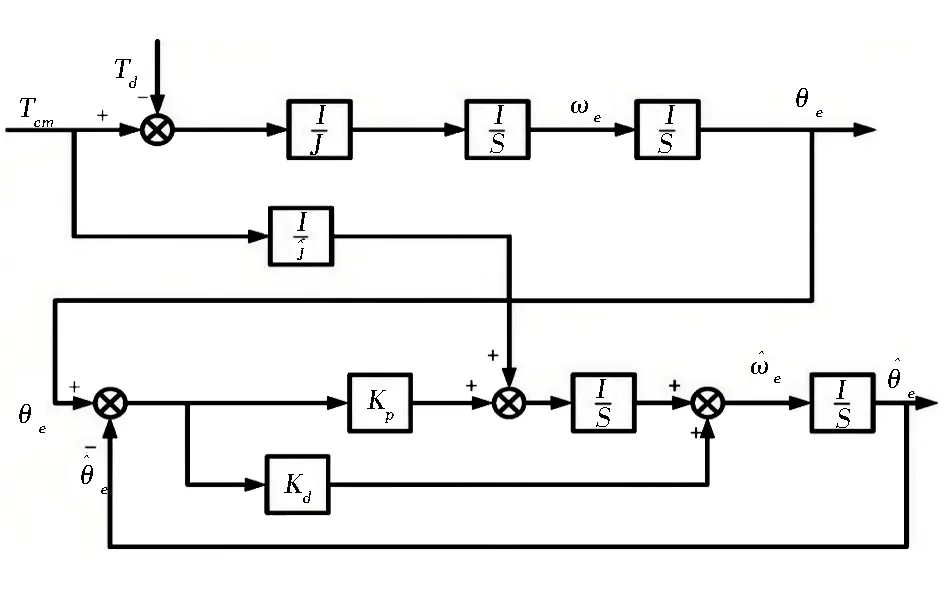
图5 基于SPMSM的龙伯格状态观测器结构

(19)

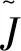
根据上述理论设计基于高频注入法SPMSM无速度传感器控制系统框图如图6所示。

根据图6搭建如图7所示的控制系统仿真模型。

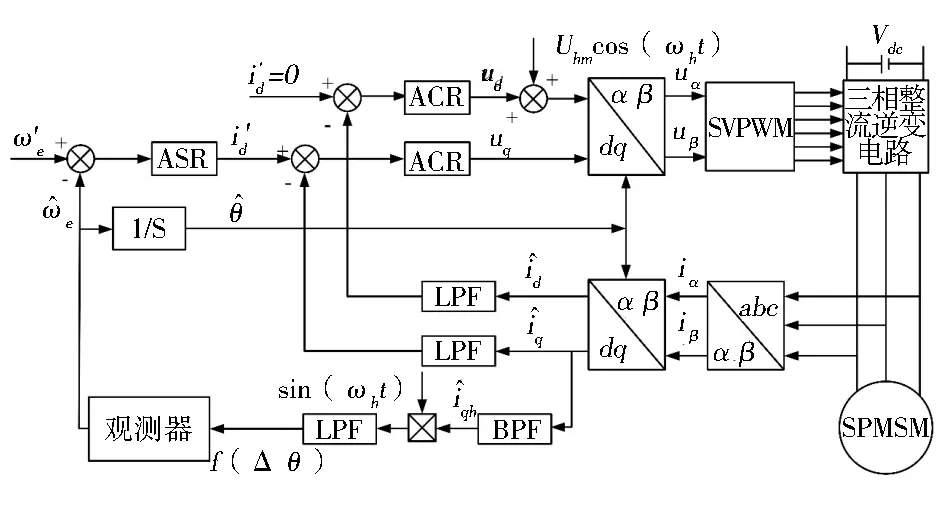
图6 控制系统框图

图7 控制系统仿真模型

4 仿真建模与结果分析

为验证上述理论的可行性,对基于高频注入法的SPMSM无速度传感器控制系统进行仿真验证。仿真参数如表1所示。

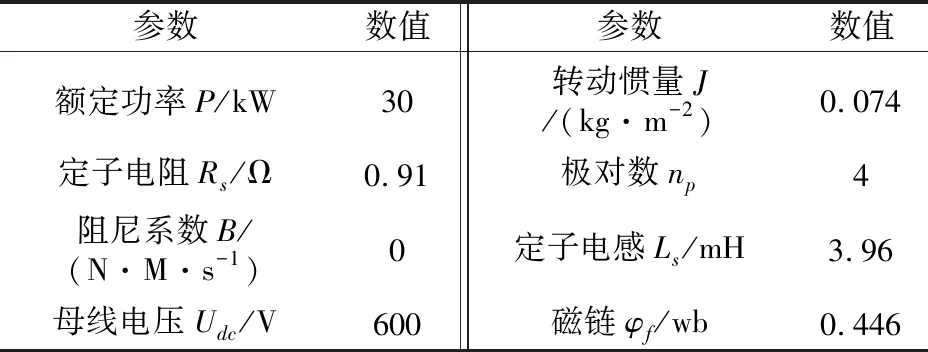
表1 SPMSM仿真参数

仿真设定矿用带式输送机SPMSM启动后转速逐渐升至150 r/min,当系统运行到2 s时,设定转速逐渐上升至300 r/min;当系统运行到5 s时,突加持续2 s的负载转矩TL=6 N·m,系统仿真结果如图8～图12所示。

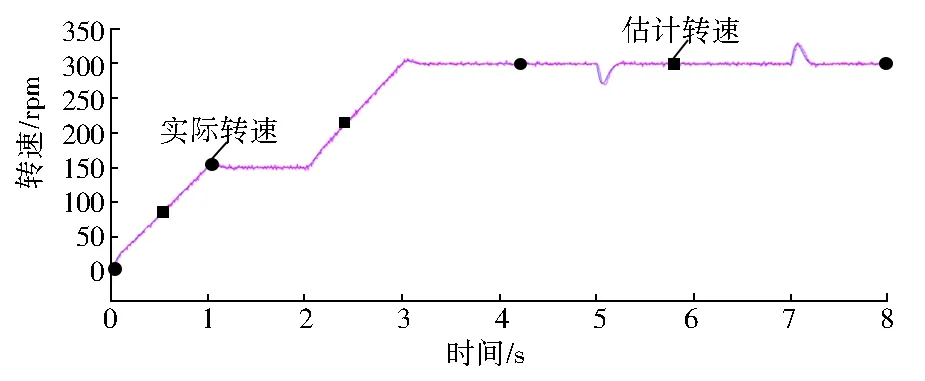
图8 实际转速与估计转速

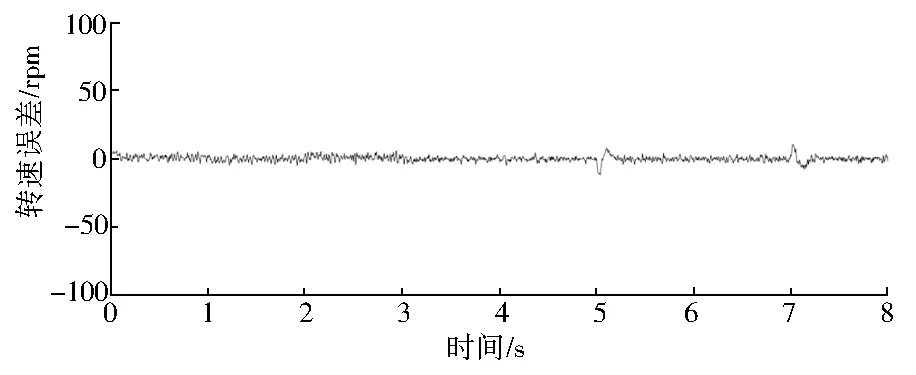
图9 转速误差

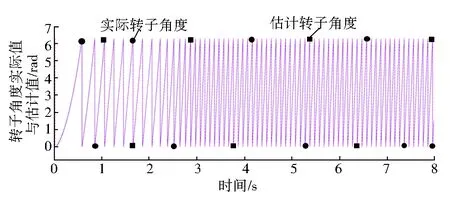
图10 实际转子角度与估计转子角度

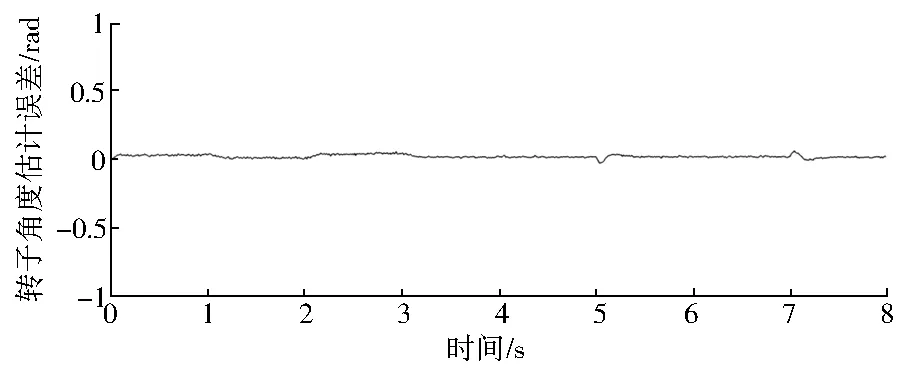
图11 转子角度估计误差

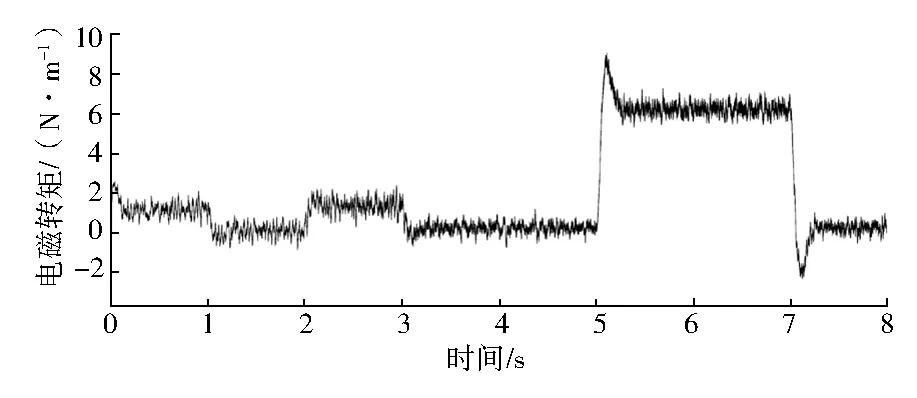
图12 电磁转矩

通过控制系统仿真结果可知,当参考转速改变或突加负载转矩时SPMSM能够快速响应并跟踪设定参考值,实际转子与估计转子的误差也能稳定在0值附近,验证了所设计的基于高频注入的带式输送机SPMSM无传感器控制系统的鲁棒性。

5 结 语

矿用带式输送机在低速运行时电机转子信息难以检测,为此提出一种基于高频注入的控制方案。该方案建立了信号激励下的SPMSM数学模型,设计了基于高频注入的转子信息观测器,并在MATLAB/Simulink中进行了验证,仿真结果验证该方案的有效性和可行性,可满足矿用带式输送机在低速运行时的控制要求。