应用于电弧增材制造技术的变层厚分层切片算法
刘帅旗,刘仁培,李忠民,杜心伟,沈泳华
(1.南京航空航天大学,南京,210000;2.天润工业技术股份有限公司,威海,264413)
0 序言
电弧增材制造是利用电弧沉积丝材的方式进行失效构件修复、生产制造新构件的常规手段,目前的电弧增材制造技术以机器人电弧堆焊为主,机器人电弧堆焊成形效率高、焊接性能稳定、增材成形良好,适用于大型复杂构件的修复和制造[1-2].
电弧增材(再)制造时,沉积层厚的控制是影响增材制造性能的关键因素,如果模型切片层厚设置高于实际沉积高度,则机器人在制造过程中易产生脉冲极限、撞枪等机械故障或者产生咬边等缺陷;如果模型切片层厚设置低于实际沉积高度,则在增材制造过程中易产生未达到尺寸要求、未熔透、局部熔覆填充不足和凹陷等缺陷.因此,对电弧增材(再)制造过程的层厚的准确控制十分重要.
目前,对于电弧增材制造的模型切片算法主要有两种,一种是等厚分层[3],即每一层的切片厚度都是一个定值;另一种是根据结构件的分型面而确定的自适应层厚切片算法[4-6].这两种方法各有优劣,前者方法简单,但会产生较大的加工余量,造成浪费,后一种算法保证了结构件的轮廓,但对结构件的外形依赖较大,且算法复杂,易产生偏差.
实际生产中,电弧增材制造的层厚确定方法通常根据经验获得,需要在平面基板上对一组工艺参数进行大量的试验,从而确定单道焊接层高[7],再根据不同情况下的焊道搭接率取其平均高度,即可得到切片厚度.但是对于复杂构件,由于包络圈形状的不同和包络圈与填充部分的比例不同,会导致包络圈路径与内路径的搭接率也随之变化,这种情况会导致在实际堆焊过程中,单层堆积厚度并不会严格遵守由平板堆焊试验所得到的厚度.因此,对分层切片时厚度参数的精准把握,是对实现高质量电弧增材(再)制造控形与保性的基础前提.
文中提出了一种变层厚的模型分层切片算法,基于对模型处理后的每个分层面的面积和对应片层下的路径长度,在特定的焊接参数下求得片层的实际层高,并通过算法的迭代,将片层厚度误差保证在一定范围内,得出其影响层厚的规律,并将其应用于离线编程系统中,以期为实现电弧增材制造过程中的精准层厚控制提供计算方法和理论依据.
1 算法流程
大型复杂构件电弧增材(再)制造时,通常采用包络圈路径与Zigzag(往复型)内部填充路径相结合的复合填充方法[8].这种复合式方法具有包络圈路径的成形精度,同时兼具Zigzag 扫描路径的算法简单、易实现的特点.但是在实际生产中,由于包络圈和结构件内壁间距、包络圈与内路径之间的距离相较于内路径之间的搭接距离难以把握,使得单层堆焊中出现边缘与内部填充高度不均或出现边缘缺肉等问题.为了解决这些问题,提出了模型变层厚切片的算法,结合复合式填充路径,实现对修复过程中的精准成形,具体流程如图1 所示.

图1 变层厚分层切片算法流程Fig.1 Flow chart of variable layer thickness slicing algorithm
算法首先通过对模型的处理,获得要堆焊部分的3D 模型,然后通过单道焊接试验确定合适的焊接参数,测量最优焊道的熔宽和余高.利用获得的焊道余高对模型进行单次切片,熔宽结合适当的搭接率对切片层进行复合路径规划,计算对应切片层沿厚度方向的平均面积.通过上述确定的焊接参数计算实际切片层厚,并与单道焊试验余高进行误差计算,进一步确定该切片层的实际层厚.通过对模型逐层计算切片层厚,并将切片层的路径保存,从而实现对模型的精准切片.
算法中,单焊道成形参数决定了切片层厚度及路径规划的标准;模型前处理关系到结构件3D 模型的精度;对模型实际切片层厚的计算(变层厚分层切片算法)是实现精准切片的基础.针对上述3 个关键问题进行具体的叙述.
1.1 单焊道成形参数
单焊道成形试验对指导实际生产制造具有重要意义.对于电弧增材(再)制造来说,针对不同尺寸下的工件,通常会根据实际情况确定采用的焊接方法、焊接材料、焊丝直径、焊接电流、电弧电压、送丝速度和焊接速度.
采用Fronius 焊机对单道焊成形进行试验,这种焊机具有参数一元化调节特性,即焊接电流取决于送丝速度.试验在不同焊接速度、送丝速度下,探究两者对焊道成形的影响,如图2 所示.从图2 可以看出,随着送丝速度的增大,焊道的熔宽和余高均有所增大,其中熔宽的变化更加明显;而焊接速度对焊道成形的影响则呈现随着焊接速度的增大熔宽和余高减小的规律.
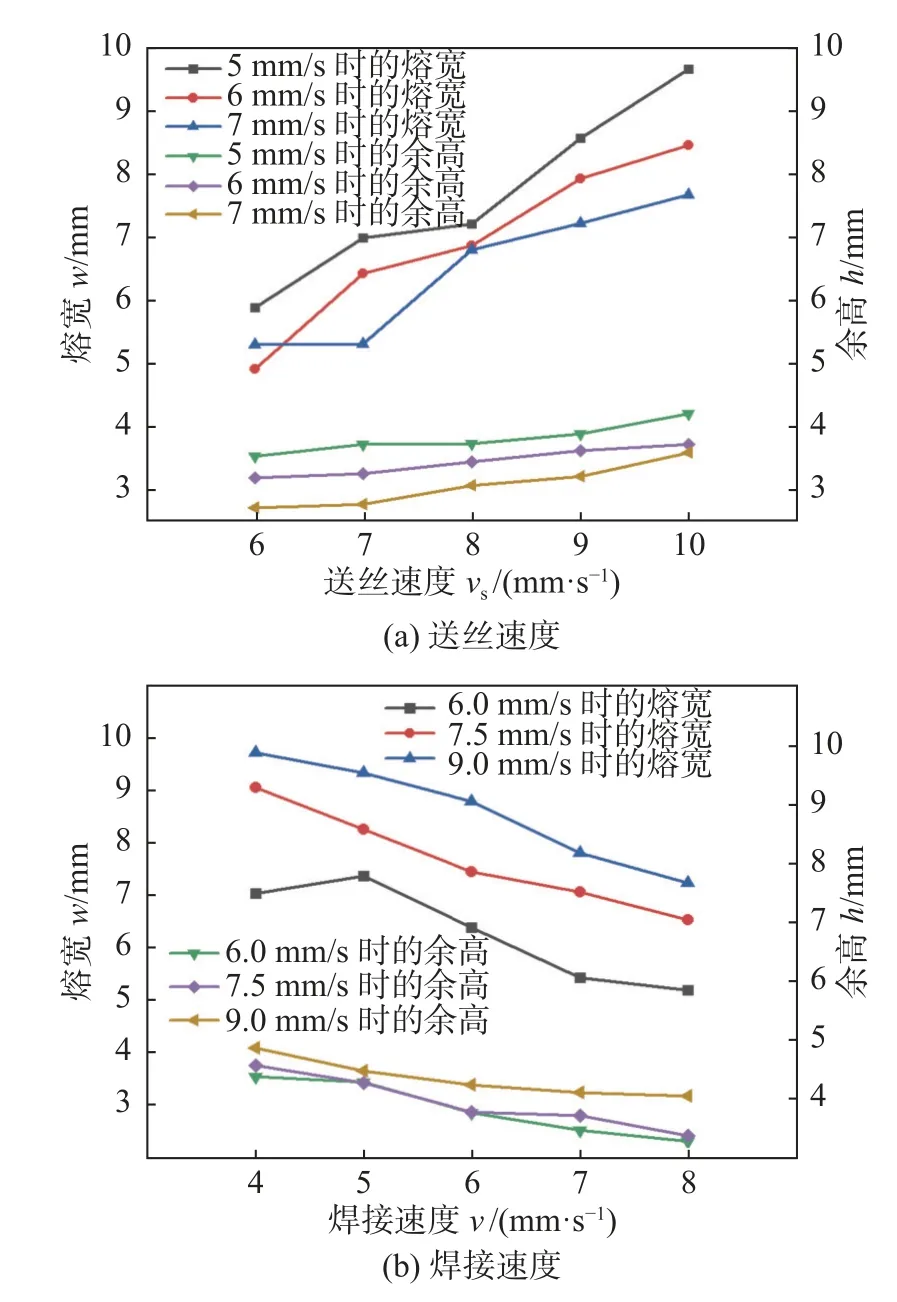
图2 焊接参数对焊道熔宽与余高的影响Fig.2 Influence of welding parameters on weld bead width and reinforcement.(a) wire feeding speed;(b) weding speed
其余焊接参数对于焊道成形尺寸影响规律不作研究.试验中根据不同的结构件采用相对应较为成熟的工艺参数,在特定工艺参数下,通过计算得到焊接过程中有效熔覆量V,即
式中:η为熔覆效率;vs为送丝速度;v为焊接速度;l为焊接路径总长度;m0为单位长度焊丝质量;ρ为熔融金属密度.
电弧增材(再)制造过程中,相邻焊道的搭接率对于零件的堆积成形同样十分重要,这个数值决定了路径规划中的相邻焊道的间距.国内外学者[9-10]建立了焊道的3D 模型,通过计算得出最佳的焊道搭接率为0.738,并进行了试验验证.因此,文中的算法对于模型切片层的路径规划,采用的搭接率在0.5~0.7 的范围内进行调整,以实现对修复件失效部位的完全填充.
1.2 模型前处理
大型复杂结构件在长期服役的环境下会不可避免地发生失效损坏,对其失效部位进行修复前,需要对该构件进行处理,具体操作如图3 所示.首先,对失效结构件进行处理,包括去除裂纹、疲劳层、清理油污和氧化层等操作.然后利用三维扫描仪获取结构件的点云数据模型,即原始数模,如图3a 所示.通过对点云数据的精简、降噪,得到精准曲面化后的结构件模型,即扫描模型,如图3b 所示.将扫描模型与结构件原始数模进行布尔求差运算,即可得到待修复区域的增材模型,如图3c 所示.最后通过对待修复模型进行切片及路径规划.

图3 模型处理Fig.3 Model processing.(a) original model;(b) scanning model;(c) additive model
1.3 变层厚分层切片算法
电弧增材(再)制造技术中通常采用等厚或者是自适应层厚算法对模型进行切片处理.这两种方法对于大型结构件来说受到一定的限制,会造成成形缺陷.文中提出的变层厚分层切片算法,可以在一定程度上减少这些缺陷,具体实现过程如图4 所示.
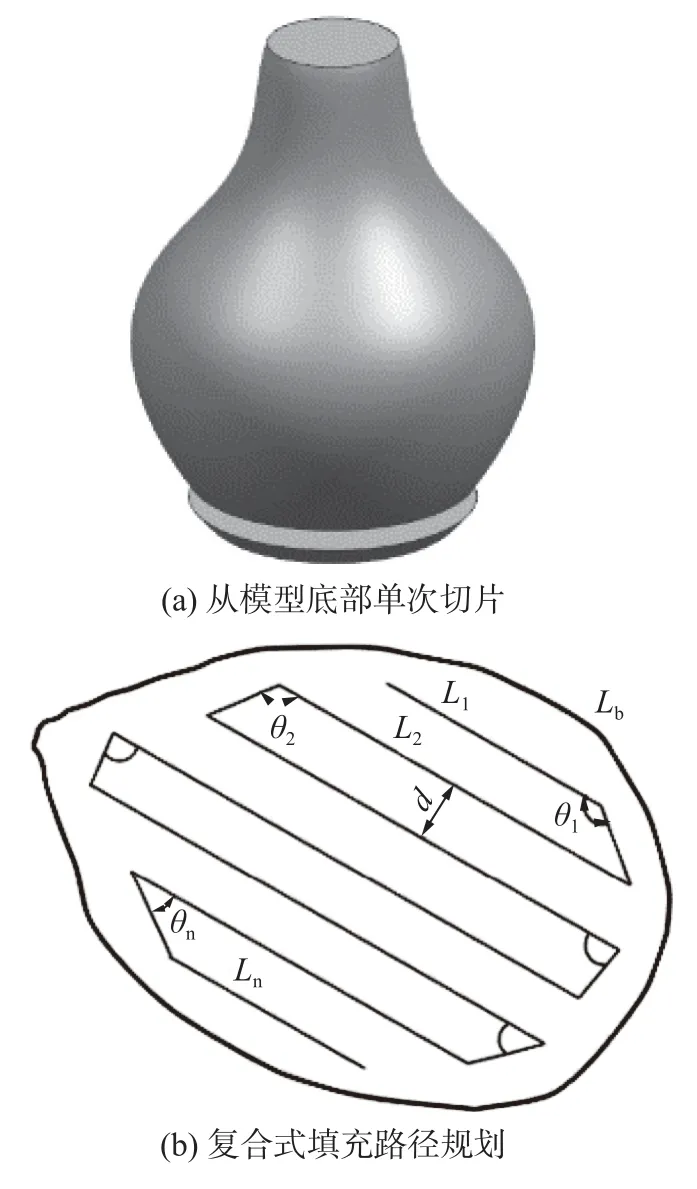
图4 模型切片及路径规划Fig.4 Model slicing and path planning.(a) single slice from the bottom of the model;(b) compound filling path planning
将之前处理好的模型,以单道焊成形试验所获得的焊道余高作为分层厚度,从模型底部对其进行单次切片,得到单个切片层,如图4a 所示.采用复合式填充路径对切片层进行路径规划,如图4b 所示.在片层的路径中,通过测量得到每一条路径的长度、包络圈路径长度和相邻路径下短路径和长路径之间的夹角.
一般来讲,应当逐层对模型进行切片以及路径规划,即每一层对应一种切片厚度以及相应的路径.但是,在完成对切片层的路径规划后,并不能直接按照该路径进行修复,否则可能会造成前文所述焊接缺陷,影响工件使用性能.解决的办法是,计算熔覆丝材的总量和切片层的体积,进行比较.利用式(1)完成相应片层熔覆过程中丝材沉积总量实际体积Vr的计算,而切片层的体积Vt为
式中:Sz为切片层沿Z轴的厚度,是一个随Z轴高度和切片层轮廓变化的值;a,b分别为该切片层的上、下表面的z值.
通常来讲,结构件修复过程中,应保证一定的加工余量,因此上述计算结果中,实际熔覆体积Vr应当大于真实片层体积Vt,反之,应重新对相应片层进行路径规划.此外,加工余量占比真实片层一定的体积分数,即
式中:e和f分别为对加工余量要求高低的上、下限.e和f均为大于0 的数,f过低可能会出现填充不足、零件尺寸偏小的问题;e过大则会导致丝材熔覆过多,造成浪费.因此,应当根据实际生产需要进行范围界定.
为了进一步确定切片层的厚度h,需要计算出切片层的平均面积.根据切片层的模型特征以及相应切片层的路径规划,也有两种计算方法.其中一种方法是利用式(2)计算所得的切片层体积计算对应切片层的平均面积,即
这种计算方法适用于切片层外轮廓曲率变化不明显或上、下面面积相差不大的模型,否则对切片层平均面积的计算将毫无意义.此外,这种计算方法仅能表示切片层模型的面积均值,而对于电弧增材(再)制造这种精度相对较低的技术来说,实际的熔覆层面积要略大于模型的实际数值.因此,这种计算方法并不适用于文中提出的变层厚算法.
另一种方法则是根据路径数据对路径所在平面进行计算,根据图4b 的标注,即
式中:S为当前切片层的面积;li为每一段长路径的长度;θj为短路径和长路径之间的夹角;lb为包络圈路径长度;w为单道焊接试验中的熔宽;d为焊接路径的搭接距离;ζ为焊道搭接率,可看作为焊接路径间距修正系数,其数值范围为0.5~0.7.
如图5 所示,cotθj项之前的负号表示当夹角为钝角时,相邻三角形未进行计算,则应当加上三角形的面积;而当夹角为锐角时,则是多计算了相邻三角形的面积,应当减去.

图5 面积计算详细Fig.5 Details of area calculation
为了计算方便,可对式(5)进行简化.对于不规则图形来说,从整体上来看,相邻路径之间拐角处的θ角中钝角和锐角的数量相近;而且对于电弧增材(再)制造这种大尺度的技术来说,拐角处三角形的面积可以忽略不计.因此,不妨假设cotθj项合计为0,即不参与计算.此外,对于切片层轮廓变化不明显的模型,轮廓线路径一般是固定的,最后一项可看做是一个常数,即k=.因此式(5)化简为式(7),即
式中:l为包络圈路径和内部填充路径长度之和.
获得切片层面积后,即可利用式(1)和式(7)计算实际熔覆层厚h.
通过式(7)和式(8)可以看出,由于路径总长度l与搭接距离d呈负相关,故层厚h与搭接距离也呈现出负相关,因此,通过调节搭接距离d可以修正切片层厚.而搭接距离d是随搭接率ζ变化的,因此通过修正搭接率就可以计算出合适的切片层厚度.最后,将该值进行误差计算,即
式中:h0为单道焊接试验中的焊道余高,n一般为5%.
如果式(9)成立,则采用h0作为该切片层层厚对模型进行单次切片;否则的话,令h0=h,即以h作为切片层层厚对模型进行处理,并重复上述步骤,对模型重新进行切片,以及上述算法中后续步骤的计算,通过迭代,将切片层厚的误差控制在n以下.
完成对模型的单次切片层厚校正后,将该层的切片层模型以及相应的路径Li保存至集合Ω,并将该片层从原始模型中去除,保证每次切片均从模型底部开始进行.重复上述步骤,得到集合即Ω={L1,L2,···,Ln},就是模型所有的增材制造工艺路径.
通过对模型逐层切片以及对各切片层厚的修正,即可实现电弧增材(再)制造中对模型的变层厚切片.
2 变层厚切片算法模拟验证
为了验证上文中的算法,采用3 种模型对其进行试验,所选模型如图6 所示.模型1 为有曲率变化的花瓶,模型2 为带有一定角度且内部中空的结构体,模型3 为不规则结构.
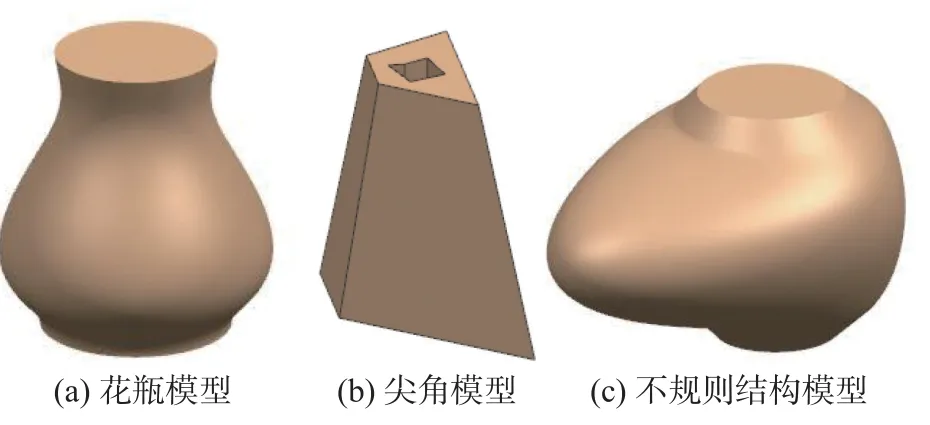
图6 3 种不同模型Fig.6 Three different models.(a) vase model;(b) sharp angle model;(c) irregular model
采用焊接工艺参数的送丝速度为6.7 mm/s,焊接速度为10 mm/s,焊道成形的熔宽为9.9 mm,余高为3 mm,搭接距离在5.0~7.2 mm 之间进行调节.将上述参数作为依据对模型进行单次切片,以及相应的路径规划,通过上文提出的变层厚切片算法对实际切片层厚与切片参数相差较大的进行调整,其结果如图7、图8 和图9 所示.从图7b、图8b和图9b 可以看出,对于外轮廓含有圆弧特征的模型,初次切片结果往往是与长路径平行的区域存在未填充或填充不足的情况,根据式(8)的计算结果也验证了实际层厚较小.从图7c、图8c 和图9c 可以看出,减小搭接距离,可以有效解决未填充或填充不足问题.而对于尖角模型边缘区域出现了过填充的现象.根据上述分析,可以通过增加搭接距离,解决这一问题.重复上述步骤,并将每层的切片模型及相应的路径进行汇总,结果如图10 所示.

图7 花瓶模型切片结果及路径调整Fig.7 Slicing results and path adjustment of vase model.(a) slice position;(b) before slice thickness correction;(c) after slice thickness correction

图8 尖角模型切片结果及路径调整Fig.8 Slicing results and path adjustment of sharp angle model.(a) slice position;(b) before slice thickness correction;(c) after slice thickness correction

图9 不规则模型切片结果及路径调整Fig.9 Slicing results and path adjustment of irregular model.(a) slice position;(b) before slice thickness correction;(c) after slice thickness correction

图10 变层厚分层切片算法完整切片结果Fig.10 Complete slicing results of variable layer thickness slicing algorithm.(a) vase model;(b) sharp angle model;(c) irregular model
3 电弧增材制造试验验证
为了进一步验证文中变层厚切片算法的可行性,对棱台模型使用变层厚切片算法,采用弧焊机器人实现棱台结构的电弧增材制造,观察和测量其成形精度与成形质量.棱台模型如图11 所示.

图11 熔覆模型(mm)Fig.11 Cladding model
采用文中提出的变层厚切片算法对模型逐层计算实际层厚,并按照计算得到的层厚对模型进行分层,然后用对应的搭接距离对切片层进行路径规划.焊接过程中各层的焊接参数均相同,即焊接电流为340 A,电弧电压为30 V,焊接速度为10 mm/s.应用上述得到的模型整体路径进行实际的熔覆得到的10 层熔覆结果如图12 所示.

图12 各层路径规划及对应的熔覆结果Fig.12 Path planning of each layer and corresponding cladding results.(a) path of second layer;(b)result of second layer cladding;(c) path of seventh layer;(d) result of seventh layer cladding;(e) overall path;(f) overall cladding result;(g) cross section of the fused forming prism
焊接过程中,每层结束后,均对当前熔覆层的几何尺寸、当前层高等数据进行多次测量,得到熔覆过程中的层高变化与各熔覆层的绝对层厚均值.每一层的工艺参数与成形尺寸如表1 所示,将上述测量得到的高度数据与对应切片层计算得到的层厚进行比较,将数据绘制如图13 所示.
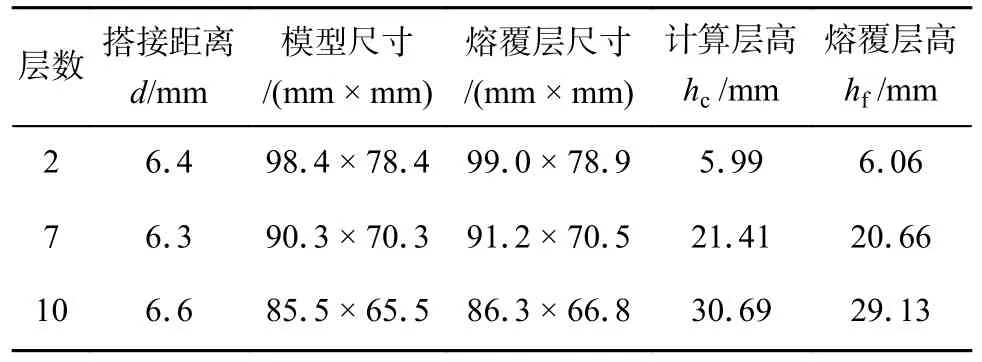
表1 熔覆层几何尺寸与层高数据Table 1 Geometric dimension and layer height data of cladding layer

图13 熔覆过程测量层高与计算层高对比Fig.13 Comparison of measured and calculated layer height during cladding.(a) height of each cladding layer;(b) height of all cladding layers
从图13 可以看出,熔覆过程中各熔覆层表面较为平整,无明显起伏波动、局部熔覆填充不足或过堆积等缺陷.通过测量值与文中提出的变层厚切片算法计算的层厚的对比可以发现,实际熔覆层厚与计算值极为接近,但从第6 层开始出现较大的偏差,这是由于熔覆过程中的热积累现象,后续熔覆层温度过高,导致实际熔覆层厚低于计算值.因此,在实际的熔覆过程中,应当保证充分的层间冷却时间.
通过上述分析,文中提出的变层厚切片算法能够较为精准地把握实际熔覆层.此外,当熔覆层数量较多时,应当考虑到层间冷却时间与熔覆层高的关系.
4 结论
(1) 针对电弧增材制造技术,提出了一种基于搭接率对实际熔覆层厚影响的变层厚切片算法,并详细给出了算法的流程,实现对模型的精准切片,可用于解决实际生产过程中因搭接率不合适而导致的缺肉、过堆积、层厚偏差等问题.
(2) 采用变层厚切片算法对棱台模型进行分层,利用弧焊机器人进行电弧增材制造试验.试验结果表明,所提出的算法成形精度高,计算结果与实际熔覆层厚极为接近,并有效解决成形不良等问题.

