基于CFD仿真的跳台滑雪空中飞行姿态优化及其验证研究

廖章文 ,周义翔 ,于经伦 ,张胜年 ,魏书涛 ,张成蛟 ,姜 峰*

(1.华侨大学 制造工程研究院,福建 厦门 361021;2.脆性材料产品智能制造技术国家地方联合工程研究中心,福建 厦门 361021;3.华侨大学 机电及自动化学院,福建 厦门 361021;4.上海体育学院,上海 200438;5.三六一度(中国)有限公司,福建 厦门 361009;6.南通大学 安全防护用特种纤维复合材料研发国家地方联合工程研究中心,江苏 南通 226019)

跳台滑雪是冬奥会重要的赛事之一，整个过程主要分为4个部分：助滑、起跳、空中飞行和着陆.运动员在起跳后0.5 s的时间内就可达到稳定飞行姿态，之后将基本保持姿态不变完成空中飞行，因此，空中飞行过程的升阻比和运动员姿态的稳定性直接决定了最终的跳跃距离[1-2].空中飞行主要受到空气流体的影响[3]，通过优化运动员飞行过程中周围的流场[4]，来获得更大的升力、更小的阻力，延长飞行距离，可以获得更好的成绩.目前对跳台滑雪空中飞行的研究方法包括风洞试验[5-6]、高速视频摄像[7-8]、传感器检测[9-10]、实地测量[11-12]以及数值分析[13]等方法进行研究.Virmavirta等[6]采用风洞试验与真实雪板相结合的方法探究在30°迎风角下，滑雪板的V型夹角和内翻相对倾角的影响，结果表明，V型夹角从0°增加到15°时，升力系数得到提高，同时滑雪板内翻相对倾角的角度变化敏感性也在增加.Seo等[14]利用高速视频摄像发现左、右脚滑雪板叉开呈V型姿态的飞行方式可以增加运动员初始的前倾角度，提升飞行过程中的气动性能.除了左、右脚滑雪板叉开呈V型姿态可以改善滑雪运动员飞行过程中的气动性能，左、右脚滑雪板内翻形成一定的相对倾角对气动性能的提升也有帮助.Bessone等[15]结合惯性传感器技术通过对来自10名运动员的100个样本进行统计分析，发现左、右脚滑雪板内翻的相对倾角范围在90°～180°之间，较小的雪板相对倾角能够改善运动员在飞行过程中的空气动力学特性.

近年来，计算流体动力学(CFD)仿真已经逐渐在跳台滑雪研究领域被使用，并且在气动特性研究方面已有相关的文献[16-19].Marqués-Bruna等[20-21]基于航空学和空气动力学的理论基础，对跳台滑雪的静态和动态、横向和定向气动稳定性机制进行探究，结果表明，滑雪板V型夹角30°和迎风角10°的飞行姿态能提高惯性阻尼和气动稳定性.Zhang等[22]通过计算流体动力学(CFD)计算全尺寸跳台滑雪的空气动力学，并与试验数据具有较好的一致性，同时解释了滑雪板的迎风角、V型姿态和内翻的相对倾角对气动性能的影响，结果显示V型角度的加入可以增强升力的产生.Lee等[23]采用有限体积法对雷诺时均方法Navier-Stokes方程进行离散分析，结合克里金模型对空中飞行过程中的稳定性进行研究，数值结果表明，迎风角、身体与滑雪板夹角、身体上部和腿之间的角度以及滑雪板内翻角度对空气动力稳定性和升阻比有影响，相对于其他角度来说，迎风角的角度变化对升阻比更为敏感，其中，最优姿态(迎风角：9°～15°，身体与滑雪板夹角：22°～28°，身体上部和腿之间的角度为160°，滑雪板内翻角度：35°)的升阻比比参考姿态提高了28.8%.

综上所述，跳台滑雪空中飞行阶段气动特性存在多因素的影响，如迎风角、身体与雪板夹角、V型夹角以及雪板间相对倾角等.目前飞行阶段的气动特性多采用CFD进行研究，主要进行身体位姿与滑雪板姿态的单因素影响分析，而对上述两者之间多因素耦合关系的研究较少.本研究将建立人/板系统的三维几何模型，采用雷诺时均方法进行模拟，选取3个主要影响因素：雪板间相对倾角、身体与雪板夹角和V型夹角.对3个因素进行正交试验，获得相应的升阻比和仰俯力矩，综合分析运动员的复杂飞行姿态与气动特性/稳定性的内在关系.

1 方法

1.1 研究对象与建模

本文中的研究对象为跳台滑雪项目中运动员与板结合的人/板系统.将人/板系统作为研究对象，通过三维软件建立实体模型，对运动员的身体特征，如滑雪护目镜、手指、面部及身体肌肉特征等进行精细化建模，如图1所示，根据Müller等[5]分析统计的结果，选取身高的平均值，即身高177 cm，滑雪板则采用京禧公司最新研发的跳台滑雪板，其长：250 cm，宽：11.32 cm，建立1:1实体模型.

Fig.1 Refined model diagram of human/board system图1 人/板系统精细化模型图

人/板系统计算区域的尺寸大小为宽2.5 m、高7 m、长度为模型前间隔4 m，后间隔9 m，如图2所示，采用该湍流模型进行外流场仿真，在长度方向上是对称边界条件，不是固定边界条件.运动员身体周围布置较细的网格单元，更精准的捕捉运动过程中的变化，为了减少计算量，采用半模进行仿真，网格总数大约为330万个左右的网格数量，如图3和图4所示.

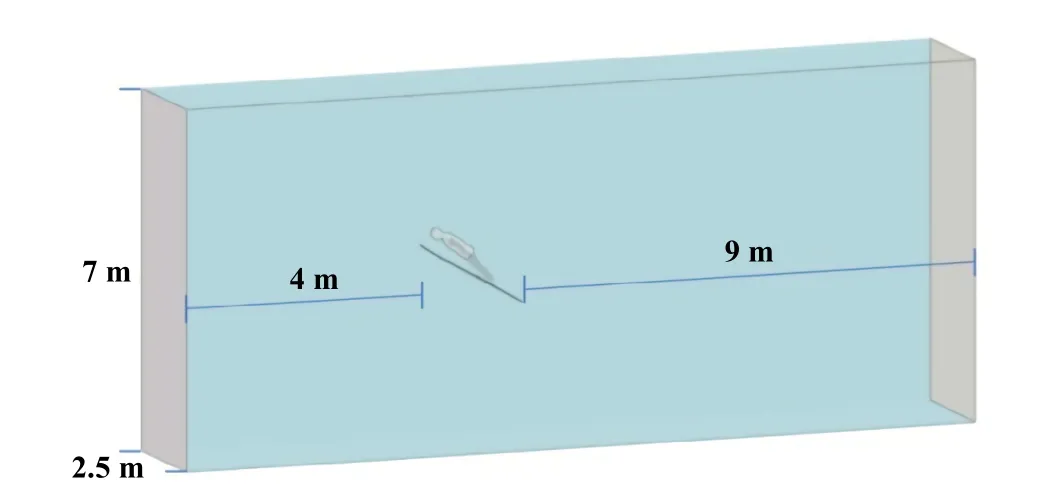
Fig.2 Calculation area diagram图2 计算区域示意图

Fig.3 Calculation area grid distribution diagram图3 计算区域网格分布示意图

Fig.4 Diagram of grid distribution of human/board system图4 人/板系统网格分布示意图

为了满足计算的要求，针对不同网格密度进行无关性验证，这里选取4种网格密度类型200～1 500万，验证结果列于表1中.结果显示，网格密度的变化并不影响最终计算结果的准确性，同样都能预测跳台滑雪的人/板系统气动特性.

表1 网格密度无关性验证结果Table 1 Grid density independence verification results

1.2 控制方程

本文作者采用雷诺时均方法进行模拟，可实现滑动界面上的复杂外部流动模拟.使用k-ε模型与k-ω模型[24]，其中，k-ε模型是1个半经验公式，需要求解模型公式中的湍动能与耗散率方程，适用于完全湍流的流场模拟；k-ω模型主要应用于壁面束缚流动和自由剪切流动.其控制方程如下：

质量守恒方程如式(1)：

动量守恒方程如式(2～4)：

其中，ρ是流体密度；p是压力；常数μ是动力黏度；u、v、w是流体在t时刻，在x、y、z方向上的速度分量；Su、Sv、Sw是广义源项，式(2)、(3)、(4)又称Navier-Stokes方程，简称N-S方程，忽略黏性的N-S方程即为欧拉方程.

能量守恒方程虽然是流体流动与传热问题的基本方程，但是对于不可压缩流动，若热交换很小以致可以忽略，可不予考虑，仅联立连续方程和运动方程求解即可.

力矩与阻力：

①表面上绕轴力的力矩(M)定义如式(5)：

②表面上的力计算如式(6)：

③表面上的力计算如式(7)：

其中，pf为面静压，af为面网格面积矢量，pref为参考压力.根据定义，流体将在表面上施加此力.

④表面上的剪切力计算如式(8)：

其中，Tf为面f上的应力张量，此剪切力通过流体施加在表面上.

1.3 边界条件与计算工况

边界条件为进口流速设定28 m/s (100 km/h)；出口压力设置为海拔1 700 m处的大气压；其他壁面为无滑移边界条件；气体为不可压缩空气，温度为-5 ℃；重力常数设置为g=9.807 m/s2.

跳台滑雪运动员在空中飞行阶段的姿态参数涉及到迎风角α、雪板间相对倾角σ、身体与雪板夹角θ以及V型夹角λ等，如图5和图6所示.参考Müller等[5]及Bessone等[15]的研究成果，结合视频解析法确定了雪板间相对倾角范围：90°～180°，身体与雪板夹角范围：18°～30°，V型夹角范围：28°～40°.

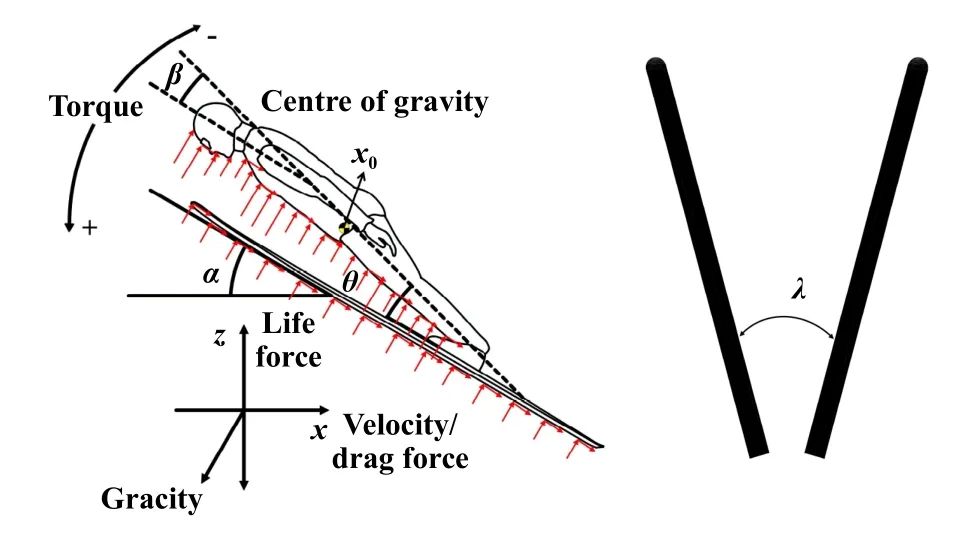
Fig.5 Air flight phase parameter diagram图5 空中飞行阶段参数示意图

Fig.6 Schematic diagram of relative inclination between skis图6 雪板间相对倾角示意图

本研究中采用正交试验设计的方法分析跳台滑雪多因素耦合关系下的流体仿真.其中，雪板间相对倾角σ分别取值为90°、120°、150°和180°，身体与雪板夹角θ分别取值为18°、22°、26°和30°，V型夹角λ分别取值为28°、32°、36°和40°，同时迎风角α为30°、上半身弯曲的角度β=18°、质心和支点x0、速度V=28 m/s (100 km/h).根据上述的参数完成流体仿真需要的正交表，对正交表的每个组合进行人/板系统模型的建立，之后进行仿真.运动员在飞行过程中主要受到升力和阻力，这里以升阻比r为目标函数来衡量气动特性的优选，如式(9).同时这些力多数相对质心x0都有一定距离，会产生不同的力矩，因此将人/板系统所受到的力矩分为2类：“+”俯力矩表示力矩作用整体逆时针旋转，“-”仰力矩表示力矩作用整体顺时针旋转.

其中，L表示升力；D表示阻力；CL为升力系数；CD为阻力系数.

升力系数与阻力系数的定义分别如式(10)和(11)：

其中，ρ表示密度；V表示入口的速度；a表示参考面积，即模型在垂直于流体方向的投影面积.

2 正交试验设计方案

本次研究涉及到跳台滑雪的多因素耦合分析，选取其中的3个主要因素，通过CFD仿真方法进行三因素四水平的仿真试验，试验的模型达到43=64个，模型量较大，因此，采用正交试验设计方法进行仿真试验.对数值结果进行处理，先分析出单目标的优水平组合，再确定出多目标因素耦合时的最优水平组合，最后将得到的优水平组合再进行建模仿真，确定最终人/板系统位姿角度三因素耦合的优水平组合.利用2022年北京冬奥会实际比赛中运动员的位姿角度进行验证.正交试验是1种利用正交表来安排与分析多因素之间的交互作用.本试验将分别对人/板系统与雪板2个方面进行升阻比和力矩的影响分析.不考虑各个因素之间的交互作用，因此，选用L16(44)正交表，将模型减少至16个，进行16个模型的仿真试验，分析雪板间相对倾角、身体与雪板夹角以及V型夹角的最优位姿角度.因素水平表列于表2中.

表2 因素水平表Table 2 Factor level table

3 结果处理与分析

为探究3个试验因素耦合后不同水平的平均值对总升阻比μ、滑雪板升阻比η、身体力矩ϕ、滑雪板力矩ψ等飞行过程中气动特性的影响，根据仿真结果进行后处理，获得平均性能参数完成指标趋势图的绘制，并进行理论分析(注：升阻比越大表示气动特性越好；力矩越小表示运动员更容易保持飞行姿态稳定).

3.1 直观分析法

运用正交试验数据处理方法中的直观分析法计算数值结果的每个因素水平对应的影响.

首先以A因素的4个水平对应的总升阻比μ为例说明计算过程.A因素的1水平，命名为A1，依次雷同.

由附录A可以看到，A因素水平的A1对空中飞行性能参考指标影响在第1～4号试验中体现，A2的影响在第5～8号试验中体现，A3的影响在第9～12号试验中体现，A4的影响在第13～16号试验中体现.其中：K表示某一水平下，对应因素的试验结果之和；k表示K的平均值.

A因素的第1、2、3、4水平所对应总升阻比之和分别为

因此，A因素的第1、2、3、4水平所对应平均总升阻比为

其他因素水平对应的空中飞行性能参考指标按照此例依次进行计算，此处将不再赘述.

3.2 趋势图分析

3.2.1 雪板间相对倾角影响分析

图7所示为不同滑雪板间相对倾角对飞行过程的影响情况.图7(a～b)所示为不同滑雪板间相对倾角对升阻比的影响，总升阻比与滑雪板升阻比有着相同的变化趋势，在90°时为最小值，随着角度的增大，呈现先增大后减小的趋势，在120°时达到最大值.雪板间相对倾角过小产生的升力不足，角度过大则产生的阻力增加，从而造成升阻比的降低.图7(c～d) 不同滑雪板间相对倾角对力矩的影响，随着角度增加受力面积增大，呈线性趋势.身体受到的是仰力矩，随角度增加力矩值呈线性增大的趋势，主要受到滑雪板的受力面积变大影响，但力矩值变化的幅度较小.滑雪板力矩在90°时，为仰力矩，大于90°时，为俯力矩，随角度增加呈增大的趋势，力矩值变化的幅度较大.

Fig.7 Effect of different relative inclination between skis on flight process图7 不同雪板间相对倾角对飞行过程的影响

3.2.2 身体与雪板夹角影响分析

图8所示为身体与雪板夹角对飞行过程的影响情况.图8(a～b)所示为身体与雪板夹角对升阻比的影响，总升阻比与滑雪板升阻比都随着身体与雪板夹角增大呈先增大后减小的趋势，在26°左右范围内升阻比达到最大值.图8(c～d)所示为身体与雪板夹角对力矩的影响，滑雪板力矩在小于26°时，主要受到俯力矩，随着身体与雪板夹角的增大，呈现递减的趋势，在30°时，主要受到仰力矩.身体力矩则主要受到仰力矩，随着角度增大呈先减小后增大的趋势，在26°达到最小值，力矩值变化的幅度较小.身体与雪板夹角在18°和30°时，升力虽然增加，但是阻力增大的幅度大于升力，使得升阻比降低.身体力矩变化幅度不大，但滑雪板力矩变化较大，由于角度增加滑雪板后端与身体的距离增加改变了流体状态，进而使得力矩发生改变.

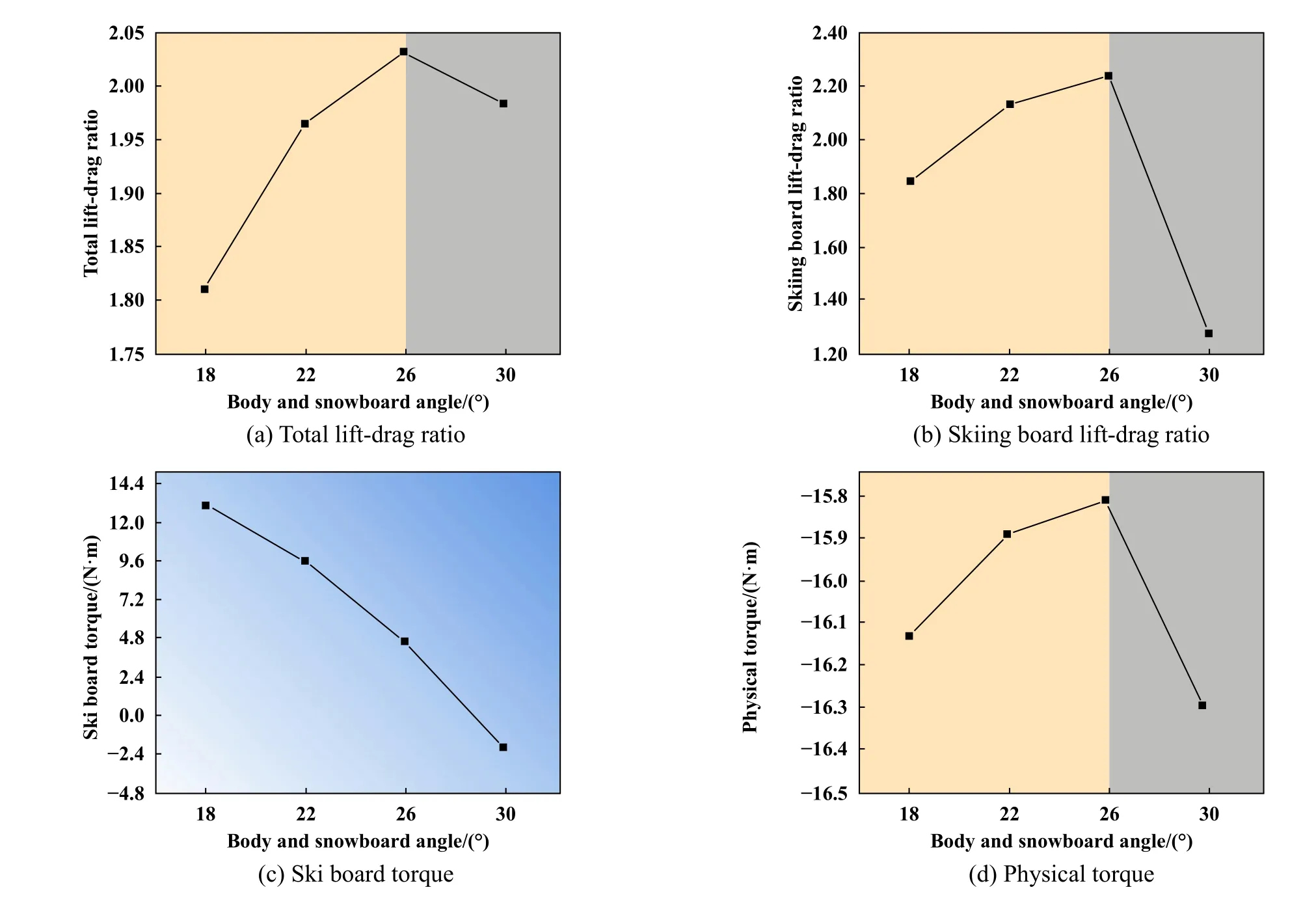
Fig.8 Effect of different body and snowboard angle on flight process图8 不同身体与雪板夹角对飞行过程的影响

3.2.3 V型夹角影响分析

图9所示为不同V型夹角对飞行过程的影响.如图9(a)所示，总升阻比随着V型夹角的增大，呈现减小的趋势，但是28°与32°的升阻比值相差不大.由图9(b)可知，滑雪板升阻比则随着V型夹角的增加先增大后减小，在32°时达到最大值.图9(c～d)所示为不同V型夹角对力矩的影响，由图9(c～d)可知，滑雪板力矩主要为俯力矩，随角度增加呈现先增大再减小，在28°时为最小值.身体力矩主要为仰力矩，随着V型夹角的增加，呈线性增大趋势，在28°时为最小值，身体仰力矩大于滑雪板俯力矩为主要影响.V型夹角在28°时的升阻比与32°相差不大，随角度增大到40°滑雪板的阻力增加明显，使得升阻比较低，间接拉低了总升阻比的值.角度增加滑雪板与身体重合度减小，从而使力矩值产生一定的增大.

Fig.9 Effect of different V-shaped angle on flight process图9 不同V型夹角对飞行过程的影响

3.3 确定单目标优化的优组合

根据正交表的仿真计算结果，分别比较各因素4个水平对应的平均飞行过程中的气动特性，可以确定单目标最优水平组合.下面以因素A的总升阻比为例进行阐述.

由正交试验设计的数据处理方法可知，根据kA1、kA2、kA3和kA4的大小可以判断A1、A2、A3和A4对总升阻比μ的影响大小.kA1>kA2>kA3>kA4，所以可以断定A1即为总升阻比而言的最优水平.

其他试验因素对应各优化目标的优化水平筛选过程与以上类似，不再单独赘述.通过筛选得到以总升阻比μ、滑雪板升阻比η、身体力矩ϕ和滑雪板力矩ψ为优化目标的最优水平组合，具体列于表3中.

表3 单目标优化的最优水平组合Table 3 Optimal level combination for single objective optimization

根据前面对趋势图的分析，可以得到雪板间相对倾角与身体与雪板夹角的最优水平组合为A2 (120°)与B3 (26°)，其中V型夹角通过分析趋势图发现C1(28°)与C2 (32°) 2个角度的优选不能直观看出.因此，针对V型夹角则同时选取2个优水平组合A2B3C1和A2B3C2，这2个优水平正好出现在单目标优化所得4个最优水平组合中，因此，只需对4组最优水平组合进行仿真.

图10所示为4个优水平组合的人/板系统压力分布图.从人/板系统中运动员的人体来说，4个优组合的分布规律也较为相似，主要的高压力区集中在前额、前胸、胯关节、踝关节以及脚趾前端等部位，低压区域主要集中在身体侧面.

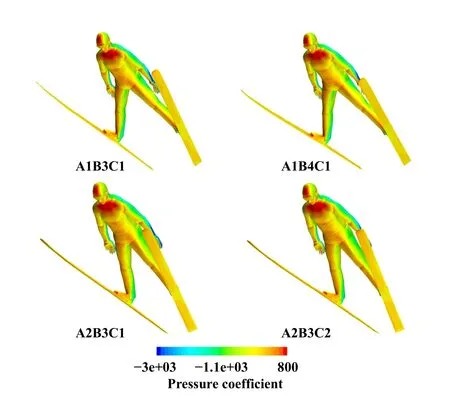
Fig.10 Human/board system pressure profile for optimal level combination图10 优水平组合的人/板系统压力分布图

图11所示为4个优水平组合的滑雪板压力分布图.不难看出，滑雪板主要的压力集中在滑雪板靠内侧的前端位置和运动员固定器脚踏部分的前端位置，滑雪板尾部以及滑雪板的板面背部的压力较小.

Fig.11 Pressure distribution diagram of ski with optimal level combination图11 优水平组合的滑雪板压力分布图

图12所示为4个优水平组合的人/板系统流场与涡量强度分布图.从侧面视角可以看到，在滑雪板与运动员的身后有多个回流涡的存在，回流涡会改变流速的方向产生一定的压力损失，加快能量耗散.在人/板系统中滑雪板下半部分的后方气流速度流线相对平滑均匀，与身后的气流速度流线的紊乱形成对比，身后的涡量强度相对较大.针对不同角度耦合的优水平组合，滑雪板产生回流涡的位置并没有明显的改变，但是强度有一定的差别，涡产生的位置主要是在滑雪板上表面的前端与脚后跟固定器的后端.运动员身后所产生的回流涡主要集中在头颈部后方和腰与胯部位的后方，可以看到优水平A2B3C2组合后方产生的回流涡强度较小，流线的分散性较好，另外3个优水平组合的涡量强度较大，所损失的能量更多.

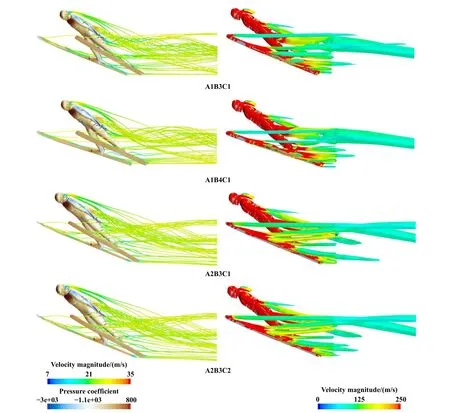
Fig.12 Flow field and vorticity intensity distribution diagram of optimal horizontal combination图12 优水平组合的流场与涡量强度分布图

从图13中我们可以看到A2B3C2组合的总升阻比与滑雪板升阻比优于A2B3C1组合，身体力矩小于A2B3C1组合，滑雪板力矩1.205 N/m略微高于A2B3C1组合的0.193 N/m.同样A2B3C2组合与A1B3C1组合相比，在升阻比方面，虽然A2B3C2组合的滑雪板升阻比2.570略高于A1B3C1组合的2.536，但总升阻比A2B3C2组合的2.153远高于A1B3C1组合的1.812，在力矩方面，A1B3C1组合主要受到仰力矩，A2B3C2组合同时受到仰力矩与俯力矩，A2B3C2组合的滑雪板俯力矩1.205 N/m略小于A1B3C1组合的仰力矩1.655 N/m，而A2B3C2组合的身体仰力矩16.051 N/m略大于A1B3C1组合的15.335 N/m，二者在力矩方面相差不大.A1B4C1组合的升阻比都远小于其他3个优水平组合，因此综合来看最优水平组合为A2B3C2，即雪板间相对倾角为120°、身体与雪板夹角为26°以及V型夹角为32°.

Fig.13 Effect of optimal level combination on flight process图13 优水平组合对飞行过程的影响

3.4 讨论

本研究中所得出的仿真结果与Bessone等[15]的研究结果相似.采用惯性传感器技术通过对10名运动员选取了100个样本进行统计分析，结果显示，较小的雪板相对倾角能够改善运动员在飞行过程中的空气动力学特性.从图7的仿真结果表明，小角度的雪板间相对倾角需要克服的力矩更小，运动员越好保持稳定飞行，升阻比更高，气动特性更好.当角度达到90°时，虽然滑雪板力矩与身体力矩需要克服的力矩依旧在减小，但是总升阻比与滑雪板升阻比却出现大幅度减小的趋势，气动特性明显降低.因此，雪板间相对倾角在三因素耦合的作用下并不是越小越好，而是在120°左右可以达到最优位姿角度，此时的升阻比达到最大值，能提供更大的升力，获得更为有利的气动特性，力矩相对较小，对稳定飞行更为有利.

针对身体与雪板夹角和V型夹角的影响分析，则是通过视频分析的方法，获得运动员在比赛过程中各方面的角度数据.这里以2022北京冬奥会的标准台(男)选手为研究对象，在央视网冬奥专题内下载比赛视频，视频帧率50 fps，分辨率3 840×2 160.选取中国、日本和欧洲运动员跳跃距离最远的一跳，将视频转码导入德国Simi Motion运动捕捉分析软件，所有视频由1名经验丰富的技术人员进行手工数字化，以减小手工带来的误差，解析获得稳定飞行人/板系统的位姿角度，如身体与雪板夹角、V型夹角以及平均跳跃距离等参数，如图14所示.由表4结果可知，欧洲与日本的运动员身体与雪板夹角偏小，变化范围在25.78±3.48°与26.18±0.96°之间，中国的运动员偏大，变化范围在29.15±4.17°之间.同样，V型夹角对比欧洲与日本选手的角度偏大一些，在33.55±4.71°和35.08±5.30°范围内，中国运动员则相对较小一些，变化范围在30.29±1.70°之间.

表4 标准台(男)研究对象基本信息Table 4 Basic information of subjects in standard desk (male)

Fig.14 Schematic diagram of video parsing图14 视频解析示意图

图8所示为身体与雪板夹角对气动特性的影响，总升阻比与滑雪板升阻比随着角度增加，先增大再减小，在26°左右达到最大值，有利于气动特性的提升.同时，滑雪板力矩随角度增加由俯力矩转变为仰力矩，身体力矩主要为仰力矩，呈先减小后增大趋势，在26°达到最小值，其中身体力矩在稳定飞行中占据主要地位.结合视频分析关于身体与雪板夹角的结果很直观地可以看出仿真结果的26°与欧洲与日本优秀选手比赛中的平均角度接近，是优选结果.同时从仿真结果来看，空中飞行过程中身体仰力矩占主要影响地位，对稳定飞行有重要作用，视频解析结果显示中国选手在比赛中位姿角度变化幅度较大，稳定性不佳，间接影响跳跃的距离，因此，优选的角度也需要运动员稳定的发挥，才能达到提升成绩的效果，后续运动员在训练中应该提升对角度姿态稳定性的控制.图9呈现了V型夹角对飞行过程的影响.从图9中并不能直观地观察分析出28°与32°哪个为最优角度.因此在确定雪板间相对倾角与身体与雪板夹角的最优水平组合为A2 (120°)和B3 (26°)后，分别对2个优水平组合A2B3C1和A2B3C2进行仿真，结果如图13所示，V型夹角32°的升阻比大于28°，拥有更好的空气特性.结合视频分析结果，可以看到各个运动员在V型夹角的变化幅度较大，但是均值也在32°附近浮动，在多因素耦合的影响下可以确定32°为优选角度.

根据单目标优化获得4个最优水平组合以及综合分析得到的最优水平A2B3C2组合分别进行仿真，结果如图13所示，人/板系统的压力在多因素耦合的作用下，如图10所示，整体的分布区域变化不大，主要集中在上半身，因此上半身的稳定控制直接影响整体的飞行稳定性.如图11所示的滑雪板压力图，可以看到滑雪板上板面的压力较小，高压区主要集中在运动员固定器脚踏部分的前端位置，而滑雪板靠内侧前端位置的高压区偏大，这也是滑雪板俯力矩较小的原因.根据不同因素耦合的优选组合，人/板系统后端所形成的速度流场存在回流涡现象，加速了能量的耗散.如图12所示，对人/板系统整体来说，优水平A1B3C1、A1B4C1和A2B3C1组合后的回流涡强度更大，更加紊乱，因此总升阻比、滑雪板升阻比都偏小；观察到优水平A2B3C2组合后的回流涡强度更小，流速的分离程度小，总升阻比和滑雪板升阻比都偏大.在多因素耦合作用下，单因素的最优水平并不一定能达到最优的气动特性以及稳定性，3个角度因素耦合后的综合最优选择更接近实际情况，更能提升运动员的气动特性以及稳定性.

4 结论

运动员竞技过程是多因素角度的耦合作用，单因素的优水平无法确保在其他位姿角度变化后也能达到最优角度，仿真结果表明主要参数的耦合关系对人/板系统的总升阻比、滑雪板升阻比、身体力矩以及滑雪板力矩均会产生影响，并能间接的影响到运动员空中飞行过程中的气动特性以及姿态稳定性.本研究采用正交试验设计的方法对人/板系统的气动特性及稳定性影响进行仿真建模与分析，并应用正交试验设计的数据处理方法结合理论分析表明了主要参数耦合的不同水平对气动特性及飞行稳定性的影响，最后通过分析得到人/板系统的最优组合为雪板间相对倾角为120°，身体与雪板夹角为26°，V型夹角为32°.获得最优水平组合后展开验证，发现较小的雪板相对倾角能够改善运动员在飞行过程中的空气动力学特性.身体与雪板夹角与V型夹角的结论，则是以2022北京冬奥会的标准台(男)选手为研究对象，通过视频解析的方法，获得稳定飞行人/板姿态的身体与雪板夹角、V型夹角以及平均跳跃距离等参数，统计得出的结果验证了本研究结果的可靠性.

附录A