Refined Spatialization of 10-Day Precipitation in China Based on GPM IMERG Data and Terrain Decomposition Using the BEMD Algorithm

Xiaochen ZHU, Qiangyu LI, Yan ZENG, Guanjie JIAO, Wenya GU, Xinfa QIU, and Ailifeire WUMAER

1 School of Applied Meteorology, Nanjing University of Information Science &Technology, Nanjing 210044

2 Key Laboratory of Transportation Meteorology, China Meteorological Administration, Nanjing 210041

3 Jiangsu Institute of Meteorological Sciences, Nanjing 210041

4 Nanjing Joint Institute for Atmospheric Sciences, Nanjing 210041

5 School of Environmental Science and Engineering, Nanjing University of Information Science &Technology, Nanjing 210044

6 School of Mathematics and Statistics, Nanjing University of Information Science &Technology, Nanjing 210044

7 School of Geographical Sciences, Nanjing University of Information Science &Technology, Nanjing 210044

ABSTRACT Continuous high spatial-resolution 10-day precipitation data are essential for crop growth services and phenological research.In this study, we first use the bidimensional empirical mode decomposition (BEMD) algorithm to decompose the digital elevation model (DEM) data and obtain high-frequency (OR3), intermediate-frequency (OR5), and low-frequency (OR8) margin terrains.Then, we propose a refined precipitation spatialization model, which uses ground-based meteorological observation data, integrated multi-satellite retrievals for global precipitation measurement (GPM IMERG) satellite precipitation products, DEM data, terrain decomposition data, prevailing precipitation direction (PPD) data, and other multisource data, to construct China’s high-resolution 10-day precipitation data from 2001 to 2018.The decomposition results show mountainous terrain from fine to coarse scales; and the influences of altitude, slope, and aspect on precipitation are better represented in the model after topography is decomposed.Moreover, terrain decomposition data can be added to the model simulation to improve the quality of the simulation product; the simulation quality of the model in summer is better than that in spring and autumn, and is relatively poor in winter; and OR5 and OR8 can be improved in the simulation, with better OR5 and OR8 dynamically selected.In addition, preprocessing the data before precipitation spatialization is particularly important.For example, adding 0.01 to the 0 value of precipitation, multiplying the small value of precipitation less than 1 by 10, and performing the normal distributions transform (e.g., Yeo-Johnson) on the data can improve the simulation quality.

Key words: bidimensional empirical mode decomposition (BEMD) algorithm, 10-day precipitation, terrain decomposition, digital elevation model (DEM), integrated multi-satellite retrievals for global precipitation measurement (GPM IMERG)

1.Introduction

Precipitation is an important climatic resource, and multi-temporal and spatial-scale precipitation data are indispensable inputs in studies of the hydrological cycle,water balance, climate, basin water resources, watershed management, and terrestrial ecosystems (Xie and Arkin,1997; Luo et al., 2008; Sun et al., 2010; Guan et al.,2018).Terrain, monsoon, and land factors such as land surface temperature (LST) and the normalized digital vegetation index (NDVI) are important reasons for the uneven distribution of precipitation in time and space (Daly et al., 2003; Ma et al., 2017a, b; Chang et al., 2019;Huang et al., 2019).At present, the spatial simulation quality of monthly-scale precipitation data is excellent,and the model coefficients are relatively stable.However,as the timescale decreases, the performance of the model will decrease, and the model coefficients will be unstable (Chen et al., 2022).

Ten-day-scale meteorological elements, such as precipitation, temperature, and humidity, are closely related to the growth period of crops and can be directly used for monitoring and early warning of crop growth (Susandi et al., 2015).At present, there are still many ways to improve the simulation quality of spatial precipitation data.There are calibrations (Ma et al., 2020, 2022) and merging techniques (Liu et al., 2019; Lyu et al., 2021; Zhu et al., 2022) to improve the quality of precipitation products, which is a method to correct the precipitation product error of a single satellite through multisource data.Interpolation methods are also commonly used to improve the quality of precipitation simulations.For example, Chen et al.(2010) used five interpolation methods, including ordinary nearest neighbor, local polynomial interpolation (LPI), radial basis function (RBF), inverse distance weighting (IDW), and ordinary kriging (OK), to realize the spatial distribution of precipitation, and noted that OK has a small error in precipitation interpolation,which is suitable for the whole region of China.Wang et al.(2014) used IDW, global polynomial interpolation(GPI), LPI, RBF, OK, and universal kriging (UK) to interpolate historical precipitation data and future precipitation data, and believed that LPI was the best among the listed methods.The interpolation method can solve the problem of spatialization, but the interpolation results cannot reflect the terrain and local characteristics, for example, it cannot reflect the characteristics of more precipitation on the windward side than on the leeward side(Zhu et al., 2018).Another spatialization method of precipitation data is to use multiple linear regression(MLR) methods to build a precipitation simulation model through multiple precipitation influencing factors.Researchers are committed to introducing new physical factors to improve the quality of precipitation simulations.Daly et al.(2002, 2003, 2008) introduced a new factor (the distance to the sea), and Zhu et al.(2018) introduced the prevailing precipitation direction (PPD) to precipitation spatialization simulation and optimized the effect of precipitation simulation.

These studies rely on real-time weather station observation data and require a dense distribution of weather stations, and the spatial distribution of weather stations directly affects the simulation quality.Recently, an increasing number of studies have adopted artificial intelligence methods in the spatialization of precipitation.Many factors, such as those influencing precipitation, terrain, and other factors, are added to the input items, and the machine model is allowed to achieve the function of modeling spatialization.Regression forest, random forest, support vector machine (SVM), boosting tree,long short term memory network (LSTM), and neural networks are widely used, and appropriate machine learning methods are selected through different approaches to improve the simulation quality (Pang et al.,2017; Bhuiyan et al., 2018; Fan et al., 2018; Ferreira et al., 2019; Shin et al., 2019; Miao et al., 2020; Zhang C.J.et al., 2020; Derin et al., 2021; Yin et al., 2021; Zhang L.et al., 2021; Zheng et al., 2021).However, certain problems, such as unclear physical mechanism, uncertainties in simulation, and weak interpretability have been raised.Better precipitation data can usually reflect local topographic features, with good simulation quality, good physical interpretability, and stable model parameters.The distribution of precipitation is greatly affected by terrain.For example, the windward slope has more precipitation than the leeward slope, but the large terrain has a blocking effect on precipitation, which can change the distribution of precipitation and cannot be reflected by MLR or artificial intelligence methods (McGovern et al.,2017).In addition to the windward slope, the slope and aspect of the large terrain also have a certain impact on the precipitation simulation, and different scales of terrain have different effects on precipitation simulation(Yang and Chen, 2008).

At present, many studies have focused on the spatialization of rainfall in complex terrain at the monthly scale(Marquínez et al., 2003; Geng et al., 2017), and good simulation results have been obtained, but research on the spatialization of precipitation under complex terrain over a finer temporal scale is still rare.However, the 10-day dataset is closely related to the growth of crops, and the production of a set of 10-day datasets can serve and guide the work of fine agriculture.Therefore, a model based on physical mechanisms is needed to fully consider the influence of terrain factors to simulate 10-day precipitation.

Bidimensional empirical mode decomposition (BEMD) is a smoothing algorithm used to decompose complex terrain.Huang et al.(1998) proposed the empirical mode decomposition (EMD) method, which is a datadriven adaptive nonlinear time-varying signal decomposition method.The EMD method decomposes the signal according to the temporal characteristics of the data itself, without presetting any basis functions (Meng et al.2019).BEMD algorithm can well decompose the altitude, slope, and aspect in the digital elevation model(DEM) data to obtain terrain decomposition under different conditions.Gu et al.(2021) used the BEMD method to test the monthly precipitation in Fujian Province,China, and found that BEMD achieved better results in the spatialization of monthly precipitation.

Global satellite mapping of precipitation (GSMaP Gauge) products outperformed other precipitation satellite products in most Chinese mainland areas on annual and daily timescales, such as Global Precipitation Measurement (GPM) and Tropical Rainfall Measurement Mission (TRMM), although the product overestimated precipitation events (Huffman et al., 2007; Shi et al., 2015;Deng et al., 2018; Lu and Yong, 2018; Salles et al., 2019;Shi et al., 2020).Xu et al.(2022) and Li et al.(2021)evaluated the performance of the most advanced satellitebased and model-based precipitation products and reanalysis data, including the integrated multisatellite retrievals for GPM IMERG, GSMaP, TRMM, Climate Prediction Center Morphing Technique (CMORPH), China Merged Precipitation Analysis (CMPA), ERA5, and ERA5-Land.They found that GPM IMERG Final product performed best in terms of precipitation events on a monthly scale, while GSMaP-Gauge overestimated the duration of precipitation.Tang et al.(2020) indicated that the IMERG Final product performed better than other products in measuring several typhoon events.In this study, we use GPM IMERG Final as the source data of precipitation, which has specific errors in various parts of the world (Murali Krishna et al., 2017; Islam, 2018; Anjum et al., 2019; Bhuiyan et al., 2020; Moazami and Najafi, 2021).For example, the error in northern China is notably large (Chen and Li, 2016), the number of precipitation events detected in lowland areas is more uncertain than that in highland areas, precipitation values in cities, water areas, and coastal areas are more uncertain than inland areas (Sui et al., 2020), and precipitation in southeastern China is relatively overestimated (Zhu et al.,2021).The reason for the large error in northern China is that satellite sensors fail to identify precipitation occurrences when surface lands are covered by snow and ice,and snow coverage in northern China is larger in winter due to its higher latitude.Therefore, it is necessary to use the data of meteorological stations to correct the satellite product.This study uses precipitation data from the China national stations (approximately 2500 stations) to correct the GPM IMERG data to obtain improved quality of the precipitation data.

In this study, we considered the impact of physical mechanisms on precipitation, and selected terrain and PPD as the factors of physical mechanisms for modeling.We used the BEMD algorithm to process DEM data with a spatial resolution of 1 km in China, and obtained elevation, slope, and aspect data at different scales (high, medium, and low frequencies).Then, we use these terrain decomposition, elevation, slope, and aspect data to construct a 10-day precipitation under complex terrain simulation, which not only provides 10-day precipitation data with higher spatial resolution, but also proves the feasibility of the physical mechanism model based on the BEMD algorithm in the mesoscale precipitation simulation of complex terrain.

2.Data and methods

2.1 Data

In this study, we select China as our study area, and the data include geographical, satellite product, and meteorological observation data.

Geographical data include administrative boundary data, spatial distribution data of meteorological stations,and DEM data.The satellite product data are the daily precipitation products of the GPM satellite product in China from 2001 to 2018 (Kidd and Huffman, 2011;Tapiador et al., 2012; Hou et al., 2014; Liu et al., 2017;Skofronick-Jackson et al., 2017).The GPM IMERG family products include IMERG Early, IMERG Late, and IMERG Final (Guo et al., 2016; O et al., 2017; Maghsood et al., 2019), and we select GPM IMERG Final as the model input.The meteorological observation data are the daily observation data of precipitation from 2001 to 2018 via more than 2400 national weather stations in China.

Figure 1 shows the spatial distribution of meteorological stations in China.Ten percent of them are randomly selected from more than 2400 stations as the model verification stations, and the nonverification stations participate in the model simulation and parameter determination.Basic information and downloads of the data are shown in Table 1.

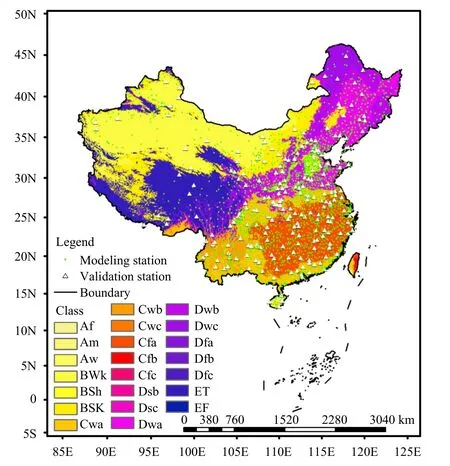
Fig.1.Distribution map of China’s meteorological precipitation simulation stations and validation stations (the meanings represented by different letter abbreviations are shown in Table 2).

Table 1.Summary of data

The daily ground observations and GPM data are processed into 10-day increments.The data include 10-day precipitation at weather stations, 10-day precipitation according to GPM, and slope, aspect, and altitude data at different decomposition scales.In this study, when the precipitation is at 0, the extremely small data less than 1 produce extra errors in nonlinear processing, and 0.01 is added to the precipitation value of 0.In addition, we use the Yeo-Johnson transformation to normalize the variables involved in the fitting due to the high skewness of 10-day precipitation to make the data meet the normality requirements of MLR.The Yeo-Johnson transformation is a nonlinear transformation and is widely used in hydrological data processing (Strazzo et al., 2019; Zhao et al., 2019).

2.2 Methods

2.2.1BEMD algorithm

The terrain data at different scales are extracted from the DEM terrain data, and the terrain data at differentscales cause certain changes to the terrain altitude, slope,and aspect data.In this study, we use the BEMD method to decompose the DEM data to obtain multiple eigenmode functions from high to low frequencies and the corresponding margins.At present, the algorithm has been widely used in the fields of image fusion, image denoising, image compression, and image enhancement(Linderhed, 2002; Nunes et al., 2003, 2005; Qin et al.,2008; Looney and Mandic, 2009).Compared with the traditional absolute height and relative height classification method (Gao, 2004) or the landform classification based on altitude and relief (Li et al., 2013), the BEMD algorithm can retain geographic information at different scales and obtain macroscopic terrain feature division without subjective influence (Gu et al., 2020).The decomposition method is:

Table 2.Köppen-Geiger climate classification

wherexis the row coordinate,yis the column coordinate, BIMFiis the microtopographic component, and Res(x,y) is the margin.The specific steps are as follows:

(1) Determine the initial DEM data fromh0(x,y)=DEM(x,y).

(2) Perform a 3 × 3 window on the DEM data to calculate the maximum and minimum values, which are upperk(x,y) and lowerk(x,y), respectively.The average of the maximum and minimum data is M ean(x,y).In addition, computehkfromhk(x,y)=hk-1(x,y)-Meank(x,y).

(3) Calculate the standard deviation (SD) based on thehkvalue.

(4) Repeat steps (1)-(3) and determine whether the SD meets the termination condition.

(5) Repeat steps (1) and (2) and determine whether the SD meets the termination condition.

The SD is an empirical value, which is generally 0.2 to 0.3 and is taken as 0.3 in this study.

(6) When SD < 0.3, obtain the first layer two-dimensional eigenmode function BIMF1, and subtract the first layer modal function from the original image to obtain the first layer margin.Repeat steps (1)-(3) for the first layer margin to obtain theN-layer two-dimensional eigenmode function and theN-th layer margin in sequence.The calculation flow for BEMD is shown in Fig.2.

The DEM, aspect, and slope are processed by the BEMD method to obtain the original, high-frequency margin terrain (OR3), intermediate-frequency margin terrain(OR5), and low-frequency margin terrain (OR8) altitude,slope, and aspect.In this research, we focus on analyzing the original DEM, OR3-scale topography, OR5-scale topography, and OR8-scale topography.

Fig.2.Flow chart of the application of the BEMD algorithm in DEM data decomposition.

2.2.2Multisource data modeling method

The magnitude of precipitation is mainly affected by weather conditions, topography, and land factors, and the topography is mainly represented by factors such as altitude, slope, aspect, and geographic location.Precipitation spatialization methods include the MLR approach and the construction that considers physical mechanisms including refined terrain decomposition.In this study, we try to compare the differences between the two methods.The MLR method constructs a model by selecting multiple factors that affect precipitation, without terrain decomposition, as follows,

whereP1is the estimated precipitation, andP0is the 10-day precipitation retrieved by the GPM IMERG Final product,his the altitude, α is the slope, β is the aspect,lon/lat is the ratio of longitude to latitude, anda0-a5are the model coefficients.

The construction with physical mechanisms including maximum precipitation increment direction and so on, is an important topic that has being extensively studied.Such a precipitation spatialization model proposed by Zhu et al.(2018) is as follows:

where PPD is the dominant precipitation direction, and its calculation method can be found in Zhu et al.(2018);b0-b5are the model coefficients.

Based on Eq.(4), the current study proposes an improved model that considers terrain decomposition at varied scales using the BEMD described above, as follows:

wherePm,n,Nis the estimated 10-day precipitation, which is from the observation results of precipitation at ground stations during parameterization;P0m,n,Nis the 10-day precipitation retrieved by the GPM IMERG Final product;hm,kis the altitude, PPDm,k,iis the dominant precipitation direction, αm,k,iis the slope, and βm,k,iis the aspect;a1m,N,a2m,N,a3m,N,a4m,N, anda5m,Nare the coefficients obtained by the model; εm,n,Nis the residual,which is obtained by subtracting the predicted value of the model from the 10-day precipitation data accumulated from the original ground station observations, that is, the part of precipitation that cannot be predicted by the model.In the parameters,mis the meteorological station number (m= 50136, 50246, …, 59954 for the 2390 meteorological observation stations),nis the serial number of 10 days (n= 1, 2, …, 36 in theN-th year),Nis the year (N= 2001, 2002, …, 2018), andkis the topography scale (k= DEM, OR3, OR5, OR8).

The selected 239 sites are excluded from the subsequent interpolation for the quality inspection of the algorithm and model.The parameters and residuals are interpolated to a grid with a resolution of 0.025° through inverse distance weighting (IDW), the interpolated parameters and residuals are extracted at the verification site location, the original model is applied to the new parameters, and the residual effect is added to obtain the final 10-day precipitation estimate.

According to different terrain decomposition data,four models are built.The model using the original DEM data is called the raw DEM model, the model using OR3 terrain decomposition is called the OR3 model, the model using OR5 terrain decomposition result is called the OR5 model, and the model using the OR8 terrain decomposition result is called the OR8 model.

2.2.3Verification metrics

In this study, we use the mean absolute error (MAE),mean relative error (MRE), and root mean square error(RMSE) to test the quality of the post simulation data.The MAE is the average of the absolute value of the difference between the simulated value and the real value.The MRE is the average of the ratio of the absolute value of the difference between the estimated value and the true value to the true value.The RMSE reflects the discrete level between the estimated value and the true value, for which the range is [0, 1], and the optimal value is 0.The RMSE is related to the value of the statistical variable, and a lower RMSE represents a smaller extreme deviation.The calculation formulas are as follows:

where MRE is the mean relative error,yiis the simulated value,xiis the observed precipitation, RMSE is the root mean square error, KGE is the original Kling-Gupta efficiency,ris the Pearson coefficient, δsis the covariance of the simulated value, δois the covariance of the observed value, β is the bias term,ais the ratio of the coefficient of variation, µsis the arithmetic mean of the simulated value, and µois the arithmetic mean of the observed value.

2.3 Process

In Fig.3, we show the overall process of this research,which contains (1) data preprocessing, (2) data extraction to sites, (3) building the model, (4) parameter calculation, (5) parameter spatialization, (6) precipitation spatial projection, and (7) model validation.In step (1), the BEMD algorithm is used to process the original DEM data to obtain three decomposition results, including the OR3, OR5, and OR8 scales.We used the precipitation data of the site to train the precipitation models based on the physical mechanism in step (3).We also spatially processed the parameters, obtained the high-resolution precipitation data affected by the terrain nationwide, and evaluated the simulation effect of the models in steps (5),(6), and (7).

3.Results

3.1 Analysis of the relationship between precipitation and terrain

Terrain is a factor affecting precipitation, and therefore, we studied the impact of terrain on precipitation.We select typical mountainous areas in China and analyze the distribution of GPM IMERG Final 10-day precipitation in mountainous areas in terms of slope, aspect,and altitude.The mountain ranges include the Tianshan,Qilian, Himalaya, Ailao, Wuyi, Tianmu, Tai, Changbai,Daxinganling, Xiaoxinganling, and Taibai Mountains,among others.The distribution and direction of the mountains are shown in Fig.4.The figure shows that the mountainous areas in western China are mostly in the northwest-southeast direction, and in the eastern part of China, they are primarily in the northeast and southwest directions.

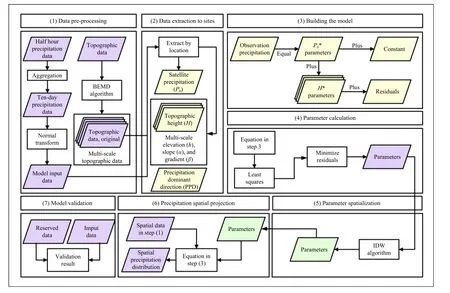
Fig.3.The technology roadmap of high-resolution spatialized precipitation simulation.

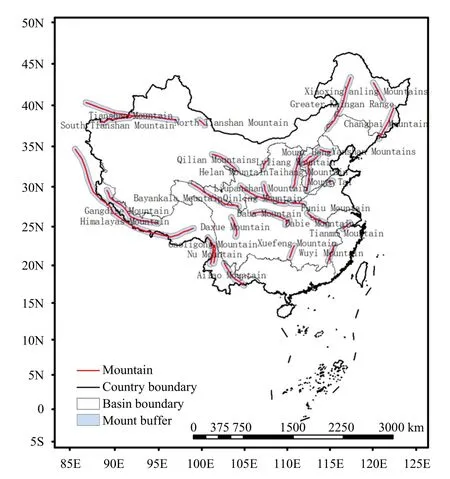
Fig.4.Distribution map of the typical mountains in China.

There are specific topographical rules in the distribution of meteorological elements, such as temperature.The southern aspects of mountains have higher temperatures than the northern aspects.The spatial distribution of precipitation has specific topographical characteristics.Fu (1992) proposed that the prevailing wind direction,slope, and aspect are related to the precipitation distribution.We selected all the typical mountainous areas in the country, including the Dabie, Wuyi, Ailao, and Qinling Mountains, to analyze their precipitation slope characteristics in GPM IMERG Final.Figure 5 shows that the aspect characteristics of precipitation across the country are not obvious, but a single mountain has obvious aspect characteristics.All aspects of the Wuyi Mountains have balanced precipitation, and the aspect characteristics are not obvious.The precipitation in the Dabie Mountains is mainly concentrated on the southeast aspect, the precipitation in the Qinling Mountains is concentrated on the northeast aspect, and the precipitation in the Ailao Mountains is also concentrated on the northeast aspect.This also shows that the preservation of large topographic features through topographic decomposition can reflect the distribution of precipitation.

3.2 Analysis of terrain decomposition

According to the BEMD algorithm, the DEM data of China with a spatial resolution of 1 km × 1 km are decomposed many times, and margins of 1-8 times are obtained.The BEMD method is a process in which small terrain is continuously discarded and the large terrain is retained.Figure 6 shows the results of the original DEM and the 3rd, 5th, and 8th margins.Figure 6a shows the original DEM data with the most detailed information.The original DEM data whose elevation values are all true values show that China’s tall terrain is mainly in the southwest region, namely the Qinghai-Tibetan Plateau region.Figure 6b shows the OR3-scaletopography.Some terrain details have been discarded,and the mountain boundaries have become blurred.Figure 6c shows the OR5-scale topography.The terrain details are further discarded.Figure 6d shows the OR8-scale topography.Compared with the original DEM, the topographic features retain only the original large topographic features, while the less undulating mountains or hills are replaced by smoothing, especially on the OR5 and OR8 scales.

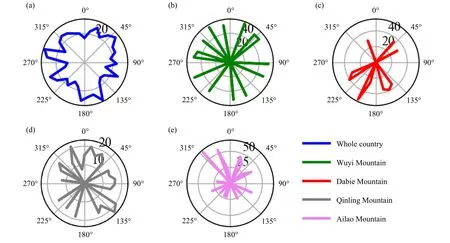
Fig.5.Wind rose diagram of the distribution of precipitation in all directions of China.

Based on the aspect data at different scales, we analyze the regularity of the weather stations and GPM IMERG precipitation of the aspect, as shown in Fig.7.Figure 7a shows the precipitation distribution characteristics of the original aspect, and the precipitation extremes are concentrated near the northwestern slope.Figure 7b shows the precipitation distribution of OR3.Precipitation is concentrated on the western, southwestern, and northwestern slopes.Figure 7c shows the precipitation distribution of OR5.Precipitation is concentrated near the southern, southwestern, and northwestern slopes.Figure 7d shows the precipitation distribution of OR8.The precipitation is still concentrated near the northwestern slope.The precipitation of GPM IMERG is generally larger than the precipitation of the meteorological station observations.The GPM IMERG precipitation aspect distribution characteristics are similar to the observation station distribution characteristics.Based on the analysis of the four scenes, the regularity of precipitation concentrated near the western slope is basically maintained, and the volatility of precipitation is gradually weakening.The terrain decomposition process is the process of retaining large terrain, and the volatility of the terrain is gradually weakening.The topographic features of OR3 and OR5 are better preserved, and the impact on precipitation is better preserved.

Fig.7.Map of 10-day precipitation changes with aspect under the decomposition of different terrains in China.(a) Original aspect, (b) OR3 scale, (c) OR5 scale, and (d) OR8 scale.

3.3 Error analysis of the simulations

In this study, we selected three evaluation indicators MRE, RMSE, and KGE to evaluate the simulation quality of the spatial products of the second 10-day precipitation in January, April, July, and October of the terrain model under different decomposition scales and MLR model.Ten percent of the weather stations across the country are randomly selected to not participate in the model parameter simulation, and these stations are used to verify the accuracy of the models, whose spatial distribution can be obtained in Fig.1.

The error analysis results are shown in Table 3.Table 3 shows that using terrain decomposition can effectively improve the accuracy of the model simulation.The 10-day precipitation quality of GPM IMERG Finaland four simulation models was compared by MRE,RMSE, and KGE.Although the MRE value of GPM IMERG Final is smaller with an average value of 0.21,the KGE value is higher than that of the other models,which means that the instability of 10-day precipitation of GPM IMERG Final is higher than that of the other models.In the four simulation models, the OR5 and OR8 models have the minimum and the second minimum values of MRE, the minimum values of RMSE and the maximum and the second maximum values of KGE; therefore, their simulation effects are better than that of the raw DEM and OR3 models.

Table 3.Error analysis of simulating 10-day precipitation by using topographic decomposition results of different scales and the MLR model (RAE, KGE, and RMSE; unit: dimensionless)

In different seasons, the simulation effect is better in summer than in April and October with smaller MRE and RMSE being smaller and higher KGE, and the simulation effect of models is the worst in January with MRE,RMSE, and KGE (0.26, 1.57, and 0.51, respectively), because the precipitation in winter is less than that in summer, which leads to many case of precipitation 0.01 in training, making the simulation results poor.

In the comparison between the 10-day precipitation simulation models based on physical mechanisms and the traditional MLR model, although the absolute error of MLR is smaller and its stability is lower, because its KGE value is lower than that of OR5 and OR8, or even lower than that of OR3, which means that the models based on physical mechanisms, especially the OR5 and OR8 scale models, are better in 10-day precipitation modeling considering the influence of complex terrain.When generating the dataset in this study, we dynamically select the best of the OR5 and OR8 models according to the evaluation quality of different 10-day precipitation periods.

3.4 Analysis of precipitation characteristics under topographic decomposition

Based on the physical mechanism models, we analyze the precipitation characteristics of the 1st-36th 10-day periods under different decomposition situations.Figure 8a shows the precipitation distribution characteristics of the original aspect.The 1st-12th and 24th-36th 10-day periods have less precipitation throughout the year.The 13th-23rd 10-day period has more precipitation throughout the year.Figures 8b-d show the precipitation characteristics under the decomposition of OR3,OR5, and OR8.Precipitation is mainly concentrated in summer, followed by spring and autumn, and the least precipitation occurs in winter.This characteristic is still maintained under different topographic decompositions.The process of terrain decomposition involves preserving the large terrain and retaining the precipitation characteristics.In terms of aspect characteristics, the southern slope has more precipitation, followed by the eastern and western slopes, and the northern slope has less precipitation.Extreme precipitation mainly occurs near the southern aspect.

Based on the physical mechanism models, we analyze the precipitation characteristics of the 1st-36th 10-day period under different decomposition elevations.Figure 8a shows the precipitation distribution characteristics of the original elevation.Figure 9 shows that precipitation is more concentrated in low altitude areas.Altitude has an impact on precipitation throughout the year.Summer precipitation is not greatly affected by altitude,mainly because it is affected by local precipitation.Winter precipitation is greatly affected by altitude,mainly because it is affected by the large-scale weather system.Precipitation is mainly distributed in low- and mid-altitude areas.The main extreme values occur in areas below 700 m.With the decomposition of the terrain, precipitation characteristics can still be retained.In the comparison of different figures, it can be found that the precipitation value in the 10th-20th 10-day period is higher in the low latitude area, due to the lower altitude and higher precipitation in the southeast of China.The precipitation in the 10th-20th 10-day period is mainly from spring to autumn in China, and the precipitation in this period is more concentrated.Therefore, the final precipitation model has good physical interpretation.

Based on the physical mechanism models, we analyze the precipitation characteristics of the 1st-36th 10-day period under different slope decomposition situations.Figure 10 shows that terrain decomposition has a serious effect on slope reduction, especially OR1-OR3.Precipitation is mainly distributed on low slopes.Slopes less than 30° impact precipitation throughout the year.Slopes less than 15° affect winter precipitation.Summer precipitation is distributed on slopes of 0-30° and lack obvious distribution characteristics.The extreme precipitation area mainly occurs when the slope is approximately 20°.As the terrain slopes are decomposed, the precipitation characteristics can still be retained.

3.5 High spatial resolution dataset of 10-day precipitation in China

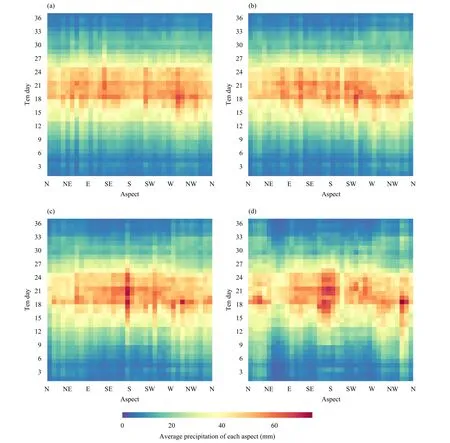
Fig.8.Aspect characteristics in mountainous regions of China’s 10-day precipitation over time.(a) original aspect, (b) OR3 scale, (c) OR5 scale, and (d) OR8 scale.

The daily GPM IMERG data are accumulated in 10-day increments to obtain a set of 10-day datasets from 2001 to 2018.We choose 2018 for display, comparing the original GPM with the simulation results.Figure 11 shows the spatial distributions of the second 10 days of January, April, July, and October in 2018.Figure 11c shows the most precipitation in summer, followed by spring and autumn, and finally, Fig.11a shows the least precipitation in winter, and Fig.11a shows that the precipitation in the second 10-days of January was mainly concentrated in southeastern China, including the middle and lower reaches of the Yangtze River and the Pearl River basin.It can be seen that the winter precipitation is too concentrated in southeastern China.Figure 11b shows the distribution of precipitation in the second 10-day of April.It can be seen that areas with more precipitation are distributed in the middle and lower reaches of the Yangtze River, the Huanghuai River basin, the Pearl River basin, and the southeast part of Qinghai Tibet Plateau.Moderate precipitation is distributed in the Huaihe River basin, the middle reaches of the Yangtze River,and the western Pearl River basin, while other areas have less precipitation.Figure 11c shows the precipitation distribution in the second 10-day of July.It can be seen that the summer precipitation represented by Fig.11c has less precipitation in the turpan basin in northwest China, and the precipitation in other regions is larger and more evenly distributed.Figure 11d shows the precipitation distribution in the second 10-day of October.The precipitation level in autumn is similar to that in spring.Nevertheless, the areas with more precipitation are different,concentrated in the middle reaches of the Yangtze River basin, Taiwan, and Hainan.

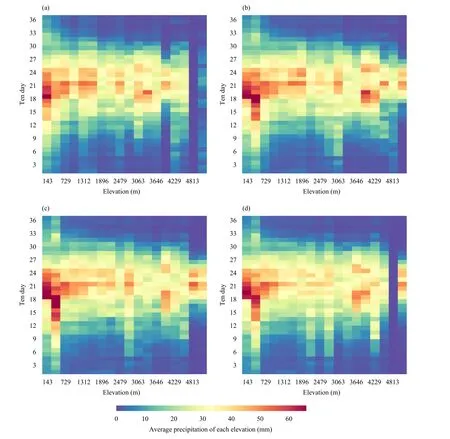
Fig.9.As in Fig.8, but for elevation.

We used the methods in this study to generate a precipitation dataset of 36 10-day per year from 2001 to 2018 in China’s first-level river basin.Figure 12 shows a precipitation dataset based on the OR5 scale with a spatial resolution of 1 km in the 2nd 10-day period of January, April, July, and October 2018.According to the previous verification results, the dataset has a higher spatial resolution and smaller error than the original GPM dataset.Based on the precipitation data of GPM IMERG Final, the spatial distribution of precipitation can be displayed more accurately and in detail.The download address of the dataset is https://github.com/GISmeteorology/BEMD_precipitation_dataset.The dataset includes the 10-yr precipitation data obtained by the original GPM IMERG statistics, the fine 10-yr precipitation data obtained by the original DEM, the fine 10-yr precipitation data obtained by OR3, the fine 10-yr precipitation data obtained by OR5, and the fine 10-yr precipitation data obtained by OR8.

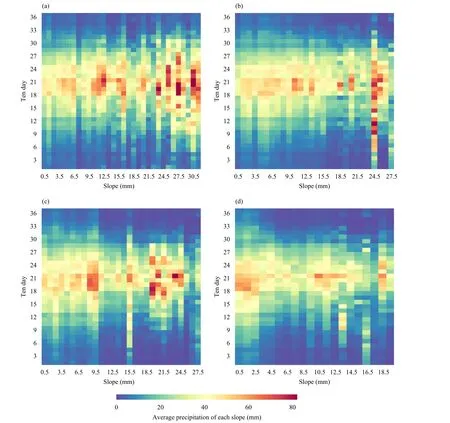
Fig.10.As in Fig.8, but for slope.

4.Discussion

In this study, a series of methods to improve the accuracy and resolution of the precipitation simulation model are found.These methods include increasing the impact factors, preprocessing the data, considering the residuals of the model, and processing the data with the Yeo-Johnson transformation.First, we add the dominant precipitation azimuth and the terrain decomposition factor, which can certainly improve the accuracy of the model simulation.Second, because small data produce additional errors during nonlinear processing, 0.01 is added to the value of 0 precipitation, the value of the smaller winter precipitation value less than 1 is multiplied by 10, and finally the simulation is restored after it is completed by preprocessing the precipitation data.The Yeo-Johnson transformation is used in nonlinear processing to preprocess the data, making the data meet the normality requirements of multiple linear regression.Finally, we add residual items, which can compensate for the simulation factors that are not considered, thus affecting the model error and improve the model accuracy.A quantitative study of the residual error in the model can reveal the proportion of the precipitation data that can be explained in the total precipitation data, and then provide a deeper understanding of the cause of precipitation.

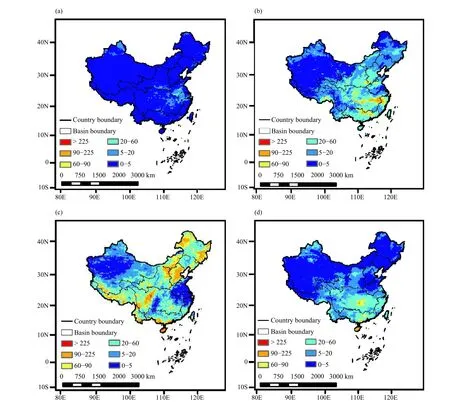
Fig.11.Spatial distributions of precipitation in China based on GPM IMERG data in the 2nd 10-day period of (a) January, (b) April, (c) July,and (d) October 2018.

This study uses the residual error of the precipitation divided by the precipitation to calculate the precipitation data that the model cannot explain by partial quantification and the difference between it and 1 represents the interpretable rate.Figure 13 shows that the residual error in July is relatively small and has a small effect, and it increases greatly in spring and winter.Figure 13a shows the interpretability of the model after adding the residual term, and reveals that when estimating 10-day precipitation based on satellite precipitation products, the residual term can improve the estimation results.In the 1st-7th and 27th-36th 10-day periods, the residual item can significantly improve the quality of the precipitation dataset by 20%.However, in the 10-day period when there is more precipitation, the addition of the residual term enhances the quality of the precipitation dataset less, by approximately 10%.Figure 12b shows the interpretability of the model with no residual term.The quality of the model without residual items is approximately 5% better than that of the original satellite precipitation product.

There are some uncertainties in this study, which largely affect the final simulation accuracy.First, the zero value of precipitation observations affects the simulation results.Second, there are many negative values in the fitted data, which is also an abnormal situation.Because it is impossible for precipitation data to have negative values, certain treatment methods need to be taken to avoid negative values.Finally, some parameters of the model are monthly values, such as the dominant precipitation direction, which also affect the construction and accuracy of the model.Different methods, such as zone modeling, single station modeling, and geomorphological modeling, also affect the model simulation results.

Fig.12.As in Fig.11, but for 10-day precipitation at 1-km resolution on the OR5 scale, simulated by using the improved model [cf.Eq.(5)].The entire dataset can be downloaded at https://github.com/GISmeteorology/BEMD_precipitation_dataset.

5.Conclusions

In this study, we introduced a terrain decomposition algorithm to construct a precipitation spatial model based on multisource data such as BEMD decomposition data,altitude, slope, aspect, and GPM IMERG Final precipitation data.We generated continuous 10-day precipitation data with a spatial resolution of 1 km in China from 2001 to 2018.We obtained the following conclusions.

(1) The terrain decomposition process shows the decomposition results for mountainous terrain from fine to coarse, micro to macro, and small to large scales.

(2) The details of elevation, slope, and aspect change with terrain classification, but precipitation is still affected by large-scale terrain features.

(3) Preprocessing the data before spatialization of precipitation can effectively improve the quality of the simulation, such as adding 0.01 to the 0 value of precipitation, multiplying the smaller winter precipitation value by 10, and using the Yeo-Johnson transformation on the data.

(4) The addition of terrain decomposition data to the simulation method can improve the quality of the precipitation simulation.Both OR5 and OR8 can better improve the simulation than GPM IMERG Final product.The better OR5 and OR8 models are dynamically selected during the simulation.

Fig.13.Analysis of precipitation interpretability of the models (a)with and (b) without residual error.

Continuously high spatial-resolution 10-day precipitation data can provide refined data support for refined agrometeorological services.Many factors affect the temporal and spatial distributions of precipitation in China,and the rules are extremely complex.We have not fully considered the impact of ground factors on precipitation.Future work will focus on reducing the influence of other factors and improving model simulation accuracy.