基于自适应滑模控制的城际列车精确停车方法研究

何兴隆

0 引言

城际轨道交通是一种大运量、快速准时、节省能源、污染少、安全可靠的出行方式，在当前的公共交通体系中扮演着重要的角色。近年来，列车自动运行系统（Automatic Train Operation，ATO）在理论研究和工程实际中都受到了广泛关注，其能在保证列车运行安全的同时使乘客出行更加舒适[1-2]。其中，列车停车精度是衡量ATO系统的重要指标之一，其目标是保证列车在设定的位置以设定的速度完成精确安全停车。列车停车控制算法不仅影响列车运行的安全性和稳定性，还会对乘客上下车的便利性和舒适度产生影响。因此，列车精准停车算法研究具有重要的理论意义和实践意义[3]。

为了使列车停车更加精确，列车停车控制系统常采用“制动曲线生成-跟踪”的控制模式[4]。在该控制方式下，ATO系统先根据列车当前位置、速度以及停车点位置等信息生成制动速度曲线，然后通过停车控制算法使列车实时跟踪该制动曲线实现精确停车。现有的ATO系统多采用PID控制（比例积分微分控制）[5]跟踪预定的制动速度曲线，实现停车控制。PID控制在控制精度以及响应时间上大致可满足停车要求，但其控制算法在控制过程中调整次数较多，稳态误差较大，影响乘车舒适度。

随着对现代控制理论研究的不断深入，一些现代控制算法被应用到ATO系统中，如自适应控制、模糊控制、滑模控制、预测控制等。文献[6]针对列车模型参数变化情况，提出自适应精确停车控制算法，并通过仿真验证了所提算法的有效性。文献[7]将模糊控制和预测控制相结合，提出了一种模糊预测控制算法。文献[8]采用鲁棒模型预测控制方法提高对外部干扰的鲁棒性，引入自触发控制策略，以进一步减少控制输出的频繁切换，提高停车过程的舒适度。文献[9]应用自适应终端滑模控制原理设计列车停车控制算法，并引入扰动观测器，仿真结果表明算法具有良好的自适应性和鲁棒性。

滑模控制因其具有响应速度快、鲁棒性强以及对扰动不敏感等优点而在工业控制领域得到越来越广泛的应用。针对常规线性滑模控制稳态性能较差的问题，本文提出一种基于自适应滑模的控制器，用自适应控制对滑模控制器的趋近律增益进行自校正调节，并将其应用于ATO系统中精确停车控制，最后通过仿真验证所设计的控制器具有良好的动态性能和稳态特性。

1 列车动力学模型

在列车运行控制的理论研究和工程设计中，常根据研究问题的复杂度和需求对列车模型进行适当的近似。单质点模型是列车自动运行控制问题中最常用的模型，典型的单质点列车动力学模型可表示为[10]

式中：M为列车总质量，t表示时间，v(t)为列车速度，F(t)为列车牵引力，B(t)为列车制动力，Rb(t)为列车基本运行阻力，Rc(t)为列车附加阻力，x(t)为列车的距离。

基本运行阻力主要由空气阻力和轮轴摩擦阻力组成，影响因素复杂，难以根据其机理建立模型，可用Davis公式表示：

式中：m0、m1、m2为阻力系数。

附加阻力主要由坡道阻力和曲线阻力组成，与列车位置相关，实际控制方法设计时可以通过线路电子地图等预先获取到。

制动过程会存在延时的现象，该过程可被近似描述为一阶延时环节，列车制动的数学模型可表示为[10]

式中：ac(t)表示由制动系统产生的加速度；at(t)为目标加速度；ar(t)表示列车运行阻力产生的加速度，其值可表示为ar(t) = [Rb(t) +Rc(t)]/M；τ和Td分别表示时间常数和时延。

由于延时环节不便于计算，可采用帕德逼近来处理式（3）中的延时环节，将ac(t)改写为

式中：λ为采用帕德逼近时引入的常数。λ与Td的关系如下：

式中：s为拉普拉斯算子。

目标加速度通过ATO的控制指令产生，在列车停车控制过程中，可近似作为线性函数处理，即

式中：c为固定系数，u(t)为控制指令计算式。

综上所述，列车制动模型可由图1表示。

图1 列车制动模型

2 自适应滑模控制器

列车停车控制过程的动态模型可以用以下状态空间方程表示：

定义误差状态方程为

式中：e1为列车位置误差，e2为列车速度误差，xr为列车参考位置，vr为列车参考速度。

列车停车过程中，需要对参考位置和参考速度进行准确的跟踪，滑模函数定义为[9]

对式（9）求导得

式中：c1为滑模面系数。

滑模趋近率采用等速趋近率：

式中：ξ为趋近律系数。

根据式（7）可得：

联立式（10）、式（11）和式（12）可得ATO精确停车系统控制律为

由于列车附加阻力Rc是有界的，因此其一阶导数和二阶导数均有界。另外，运行基本阻力Rb也有界，令

则有Q≤Qmax，则可将式（13）改写为

在实际的滑模控制中，通常选择较大的ξ来保证系统有较快的响应速度以及较好的系统稳定性，但这样会恶化系统稳态性能，产生较大的抖振。为了加快系统动态响应速度，同时保证系统稳态精度，设计了关于ξ的自适应律：

将上述自适应律与滑模控制相结合，则基于自适应滑模的ATO精确停车系统控制律可表示为

3 仿真分析

为了验证所提出的自适应滑模停车算法的有效性，在MATLAB/Simulink环境中搭建列车停车系统仿真模型，分别使用PID控制和自适应滑模控制对停车性能进行仿真验证。列车运行基本参数如表1所示。

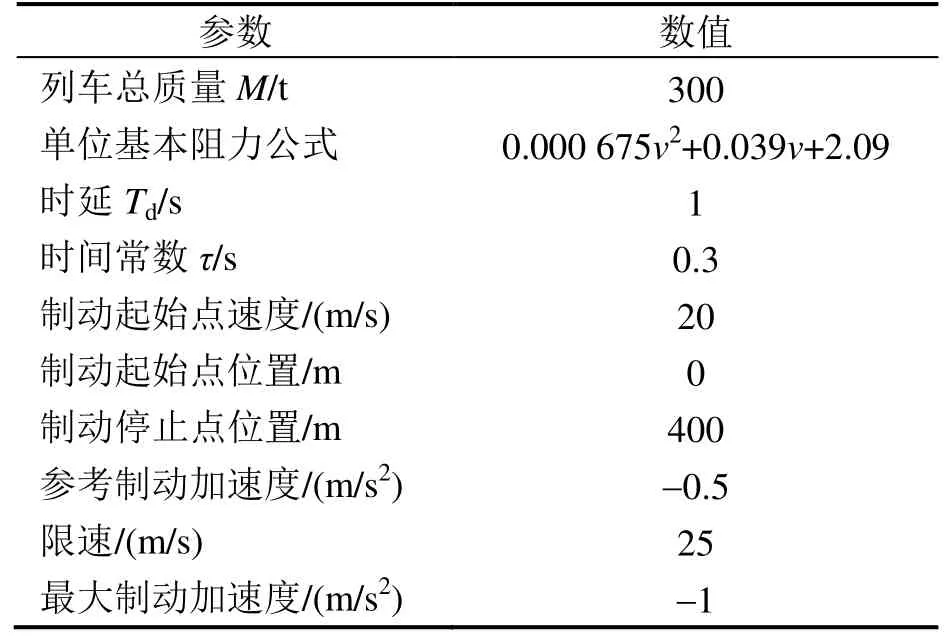
表1 列车运行基本参数

制动曲线跟踪性能对比情况如图2所示：列车开始制动时，由于制动系统中机电装置具有延时性，列车无法立即跟随参考制动曲线；经过控制器作用后，速度逐渐趋于跟随参考制动曲线。从仿真结果可以看出，自适应滑模控制可以更快地跟踪参考速度曲线，且最终达到高精度的停车效果。PID控制虽然也能跟踪参考速度，但其响应速度较慢，并且最终停车位置存在较大的误差。列车速度误差曲线如图3所示，可以看出，自适应滑模控制器在控制过程中速度误差更小。

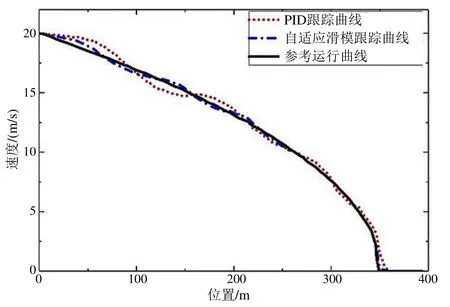
图2 速度曲线跟踪性能对比

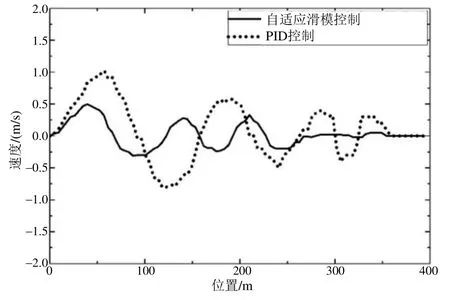
图3 速度误差曲线

两种控制器的目标加速度曲线如图4所示，PID控制在调节目标加速度时需要较长时间，整个过程中加速度变化较大。而本文所提出的自适应滑模控制，加速度仅在刚开始制动时有较大变化，然后迅速趋于稳定，加速度变化较为平稳，可保证列车较高的舒适度。

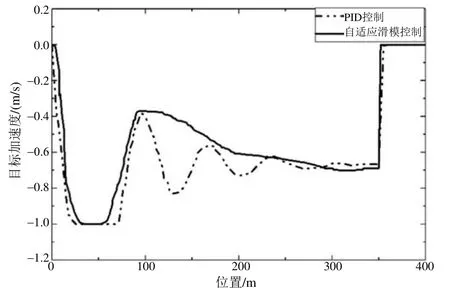
图4 目标加速度曲线

4 结语

本文提出了一种基于自适应滑模控制的列车精确停车控制方法。结合列车制动系统模型，在线性滑模控制器的基础上，为改善系统动态响应速度和稳态误差，采用自适应控制对趋近增益进行校正，并通过仿真验证了算法的有效性。通过与传统的PID控制方法进行比较分析，基于自适应滑模控的制停车算法不仅能提供快速稳定的速度跟踪以及较高的停车精度，而且在停车过程中能保证列车较高的平稳性和舒适度。