碳达峰约束下的运输结构优化研究
孙佳,孙启鹏,高捷,张士行,乔佳璐,李弢
(1.长安大学 运输工程学院,陕西 西安 710064;2.长安大学 经济与管理学院,陕西 西安 710064;3.交通运输部规划研究院,北京 100028)
气候变化问题是当今人类社会所面临的重大挑战之一。国家主席习近平在第七十五届联合国大会一般性辩论上明确提出了我国的双碳目标。国家发改委的相关数据表明,2019 年我国交通运输碳排放量约占全国碳排放总量的10%,是碳减排重点关注的领域。国务院于2021 年10 月印发了《2030 年前碳达峰行动方案》(下文简称《方案》),运输结构调整是该《方案》中实现碳达峰的重要内容和路径。而且,从大量文献研究及综合交通运输实践来看,运输结构是影响交通运输碳排放的重要因素,铁路和水运占比的增加有助于交通运输行业碳排放量的减少,而公路和民航占比的增加会导致交通运输行业碳排放量的增长[1],优化运输结构具有较大的碳减排潜力[2]。综述发现,运输结构调整优化研究主要分为两类,孙启鹏[3]根据经济学、系统科学等多学科理论,提出了优化综合交通技术结构、提高综合交通运输组织效率、政府引导与市场相结合等结构优化宏观对策;陈淑玲等[4]通过比较分析欧法美日的运输结构调整政策,建议我国发展以铁路为骨干的多式联运。以上学者在优化运输结构时采用了定性方法,而其他学者采用了定量方法,QIANG 等[5]提出了能源消耗最小化的运输结构优化模型,该模型既能减少碳排放又能最大限度地降低城市交通的能源消耗;尚玲宇[6]利用线性规划优化了2020 年广东省运输结构,该结构在满足了高效用的同时兼顾了低碳排的要求。
运输结构调整优化是理论和实践中长期关注的问题,现有研究已取得了丰富成果,但在碳达峰目标约束下,其约束条件和优化方法需要重新思考,成为当下该领域关注的热点新问题。本文首先构建交通运输业STIRPAT 模型,并以2000—2019 年作为研究区间进行岭回归探究影响交通运输碳排放的因素。基于以上模型,以2030 年碳达峰为约束条件来求解最优运输结构,为合理优化运输结构提供理论参考。
1 交通运输碳排放影响因素分析
1.1 交通运输碳排放STIRPAT模型
IPAT 和STIRPAT 模型以分解公式和指标体系对碳排放进行指标分解,主要应用于国家尺度。EHRLICH[7]等构建了IPAT 模型,用来探究人口规模、富裕程度和技术水平对环境的压力,该模型在生态经济学领域运用广泛;YORK 等[8]在IPAT 模型的基础上提出了STIRPAT 模型,认为任何对环境有影响的因素都可以纳入STIRPAT 模型中,其模型表达式为:
式中:I、P、A、T分别为环境压力、人口规模、富裕程度和技术水平;α为模型系数;b、c、d分别为人口规模、富裕程度、技术水平的指数;e为模型随机误差扰动。STIRPAT 模型允许对各影响因素适当分解,可以根据自身研究目的对模型进行扩展[9],因此该方法在交通运输碳排放影响因素研究中成为学者们比较偏好的方法。当前交通运输碳排放影响因素主要是从技术水平(能源利用效率、能源强度)、经济水平(人均GDP)、交通规模(客、货运周转量)来考虑[10-11],而调整运输结构作为实现碳达峰的重要手段之一,其对交通运输碳排放的影响亦不容忽视。据此,本文对以往模型进行改进,构造STIRPAT 模型如下:
实际分析时,通常对等式两边取对数进行降幂处理:
式中:因变量C(吨二氧化碳)表示我国交通运输业碳排放量。自变量PGDP是人均GDP(元),代表我国经济发展水平,即原模型中的富裕程度;客运周转量KY、货运周转量HY代表交通规模,单位分别为人公里、吨公里,对应原模型中的人口规模[10];E(吨标准煤/万元)是能源强度,即交通能源消耗量与国民生产总值的比值,代表原模型中的技术效用。运输结构是由公路(G)、铁路(T)、水路(S)、航空(H)运输周转量在总周转量中的占比反映的(管道运输周转量仅占我国运输周转量少量份额,故不作考虑)。另外,为避免严格多重共线性,模型中去掉了水路运输占比。因为同一种运输方式的客运和货运周转量不可直接加和,需要进行客货换算,故采用国家统计制度规定的公路、铁路、水路、航空运输客货转换系数1/10、1、1/3、1/13 进行换算。参数α为常数项,β1、β2、β3、β4、β5、β6、β7为弹性系数,表示当各自变量变化1%时,将分别引起碳排放量C的β1%、β2%、β3%、β4%、β5%、β6%、β7%的变化。
1.2 普通最小二乘法回归
选取2000—2019 年作为研究区间,人均GDP(以2000 年不变价计算)、交通能源消耗量、客货运周转量、公铁水航四种运输方式周转量等数据均来自《中国统计年鉴》,交通运输业碳排放数据取自CEADS 数据集。为了尽可能精确地把握各个影响因素与交通运输碳排放量之间的关系,先用SPSS25.0 软件对STIRPAT 模型进行普通最小二乘法回归,结果如表1 所示。回归方程总体显著性较好(F值=2 981.481、总体Sig.值=0.000),且具有很高的拟合优度(调整R2=0.999)。但模型t 检验结果不通过且lnHY、lnG、lnH的系数与预期不符,这可能是由于变量之间存在多重共线性。利用VIF值来诊断模型的共线性,VIF值均远大于10,说明模型确实存在严重多重共线性的问题。因此,必须消除模型的多重共线性才能保证模型的精确性。综上,后面采用岭回归方法进一步分析。
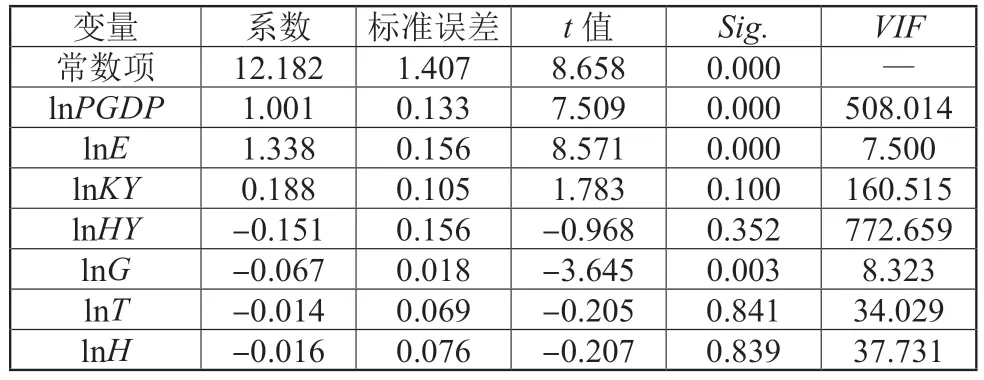
表1 普通最小二乘回归结果
1.3 岭回归分析
岭回归本质上是由最小二乘法改进得到的,相比于最小二乘法的无偏性估计,它是一种有偏性的回归方法,以部分信息的损失及精度的降低为代价拟合出更可靠的回归系数。基于SPSS25.0,设定岭回归系数K的取值范围为(0,1),数据间隔为0.01,运行程序逐一进行模型系数估算,得到岭回归K值与相应系数的变化结果(表2)。当K=0.35 时,各项自变量的系数变化逐渐趋向稳定,回归方程总体显著性较好(F值=97.99、P值=0.000),且具有很高的拟合优度和解释力(调整R2=0.973)。
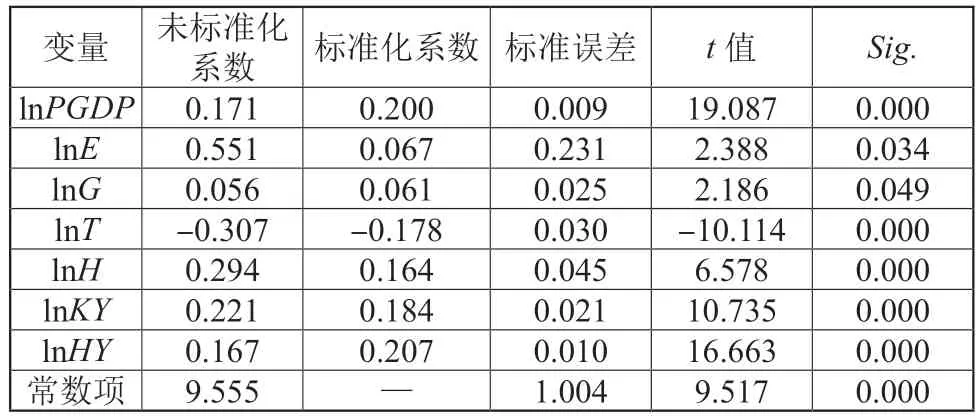
表2 岭回归结果
各因素对交通运输碳排放的影响程度大小分别为:货运周转量(0.207)、人均GDP(0.200)、客运周转量(0.184)、铁路运输占比(-0.178)、航空运输占比(0.164)、能源强度(0.067)、公路运输占比(0.061)。可以看出运输结构影响着交通运输碳排放,铁路、航空运输占比对交通运输碳排放的影响程度甚至大于能源强度的影响,公路运输占比、航空运输占比与交通运输碳排放量正相关,铁路运输占比与交通运输碳排放量之间呈负相关关系。
为了验证模型回归效果,用历史数据进行模拟,历史值与模拟值对比见图1,我们进一步计算了模型的平均相对误差为1.04%,平均绝对误差为4.82%,模型整体拟合效果比较好。
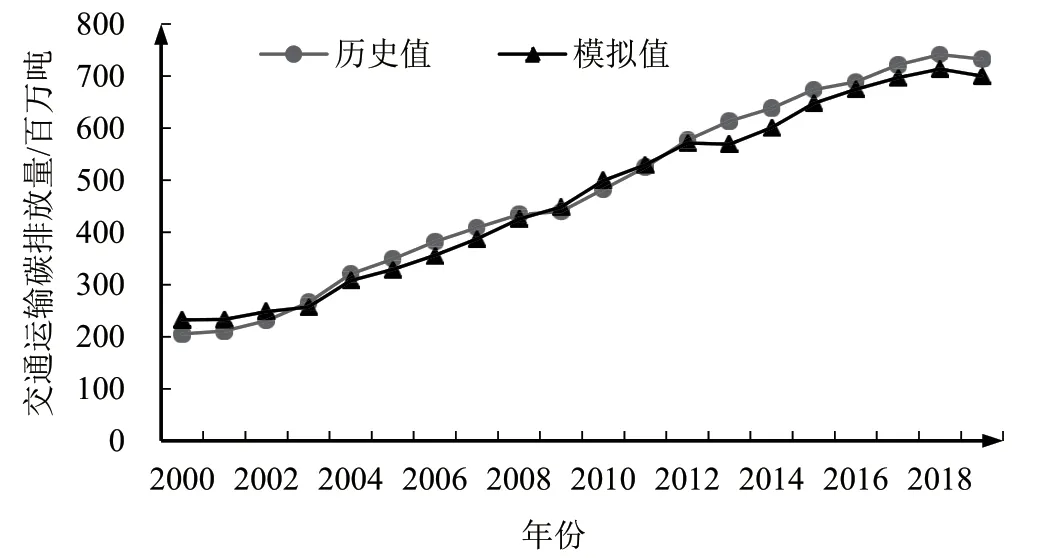
图1 交通运输碳排放量模拟值与历史值对比
2 运输结构的优化
2.1 问题描述
在前文讨论的交通运输碳排放主要影响因素中,运输结构的变动对交通运输能耗影响显著且相对容易调整,运输结构成为降低交通运输能耗、实现碳达峰的突破口。李晓易等[12]指出2021—2030 年推进运输结构优化是实现碳达峰的重要路径,运输结构优化具有较大的碳减排潜力。现有研究多是采用情景分析并加以行业判断来设定运输结构占比以实现碳达峰,但运输结构调整过程中常常会面临着为了降低交通能源消耗而导致社会运输需求得不到满足、发展低碳运输方式而忽略其他运输方式存在的价值等问题。综上所述,本文的研究问题可以归纳为:在碳达峰约束下如何优化运输结构,以保证能源消耗最小化的同时实现运输周转量最大化,本文试图给出2030 年碳达峰时的最佳运输结构。
2.2 模型假设
(1)运输方式分为公路、铁路、水路、航空运输四种(由于管道运输专用性强,与其余运输方式的相互替代性弱,运输结构优化未将其包含在内),不同运输方式提供的位移服务是可以互相替代的,乘客和货主对于不同运输方式提供的服务没有明显偏好。
(2)运输结构优化只是针对不同运输方式周转量占比的调整,暂未考虑交通运输布局。
(3)不同文献预测碳达峰的具体时间不同,多数预测在2030 年前后实现碳达峰,结合国家给出2030 年碳达峰的目标,本文不再探讨碳达峰的具体时间,而是假设2030 年我国实现碳达峰。
2.3 模型建立
本文所研究模型的变量及参数设定为:i为运输方式,取值为1~4 分别指公路、铁路、水路和航空运输;ei为第i种运输方式的单位周转量能耗;xi为第i种运输方式的周转量,为模型决策变量;Q1为最低运输周转量;Q2为最大运输周转量;C为交通运输碳排放约束值;Li为第i种运输方式的平均运输距离;Si为第i种运输方式的线路长度;αi为第i种运输方式的线路合理利用率;bi为第i种运输方式的现有占比。
构建运输结构优化模型,具体可表示为:
式(4)、式(5)分别代表运输能源消耗量最小(优化目标1)和运输周转量最大(优化目标2);式(6)为总运输周转量约束,Q1、Q2分别是2030 年经济社会发展所需的最低运输周转量和运输能力制约下的最高运输周转量;式(7)为2030 年交通运输碳排放约束,优化后的运输结构应满足2030 年碳达峰时交通运输碳排放量要求,由上文交通运输碳排放影响因素回归模型拟合出的2030 年交通运输碳排放量应不大于碳达峰时交通运输碳排放约束值C;式(8)为各运输方式的最低线路利用率约束,确保优化后的运输结构要使交通基础设施物尽其用;式(9)、式(10)则是运输结构调整的政策约束,根据《方案》“公转铁、公转水”的政策倾向,现有运输结构中的公路运输占比会下降,铁路、水路运输占比会上升,因此2030 年公路运输占比应不大于现有公路运输占比b1,铁路和水路运输占比应不低于现有铁路和水路运输占比b2、b3。
2.4 实证分析
2.4.1 参数设置
单位周转量能耗值ei:由于能源技术突破较困难,运输方式单位换算周转量能耗值采用2019 年的取值,公路、铁路、水路、航空的能耗值分别为0.170 0、0.039 4、0.025 9、4.193 4 万吨标准煤/亿吨公里,数据来源于《2019 年交通运输行业发展统计公报》《2019 年铁道统计公报》以及《2019 年中国民航行业发展统计公报》。
2030 年最小运输周转量Q1、最大运输周转量Q2:考虑新冠疫情影响,参考王靖添等[13]对客货运周转量的预测值并进行换算,本文设定2030 年运输周转量最小为257 585 亿吨公里、最大为300 600 亿吨公里。
交通运输碳排放约束值C:LI 等[14]通过文献综述了我国2030 年碳达峰时的CO2排放量,而我国交通运输碳排放量约占全国碳排放总量的10%,推断2030 年碳达峰实现时交通运输碳排放约束值在10 亿吨左右,这一取值同周伟等[15]的研究基本一致。
人均GDP:基于国际货币基金组织IMF 对中国GDP 增速的预测,设定2030 年我国人均GDP 为67 045元(以2000 年不变价计算)。
能源强度E:鉴于2030 年实现社会整体碳达峰之前能源技术进步的潜力比较小,考虑洪竞科等[16]参考情景下的2030 年交通运输业能源强度年均增长率,这里假设能源强度的变化仍延续“十三五”期间的趋势,2019 年基本情景下能源强度为0.08 吨标准煤/万元,后续能源强度年增长率为-3.2%,计算得到2030 年能源强度为0.056 吨标准煤/万元。
线路合理利用率αi:借鉴尚玲宇[6]的研究,用不同运输方式运量占比和线路里程占比之比度量,即αi=wi/zi,其中wi代表不同运输方式的客货运量占总运量的比重,zi代表不同运输方式线路里程占总里程的比重。根据《中国统计年鉴》可计算得到公路、铁路、水路、航空运输的线路合理利用率向量为:αi=(1.675 3,7.940 9,4.250 4,0.013 8)。
不同运输方式平均运输距离Li、线路长度向量Si:依据2000—2019 年的《中国统计年鉴》可计算得到Li=(94.88,615.73,911.15,2 266.48)公里,由于该值历年波动较小,因此设为固定参数;Si=(501.25,13.99,12.73,948.22)万公里。
b1、b2、b3:经计算,2019 年公路、铁路、水路运输周转量占比分别为28.74%、21.32%和49.39%。
2.4.2 模型求解
模型求解属于双目标非线性优化问题,优化目标不能同时达到最优,只能得到均衡两个优化目标的帕累托最优解集。本文采用NSGA2 遗传算法优化,该算法是带有精英保留策略的快速非支配多目标优化算法,可有效解决非线性优化问题[17]。设定算法种群数量为200,迭代次数为500 次,交叉概率为0.9,变异概率为0.1,采用Matlab 求出帕累托解集,结果如图2 所示。
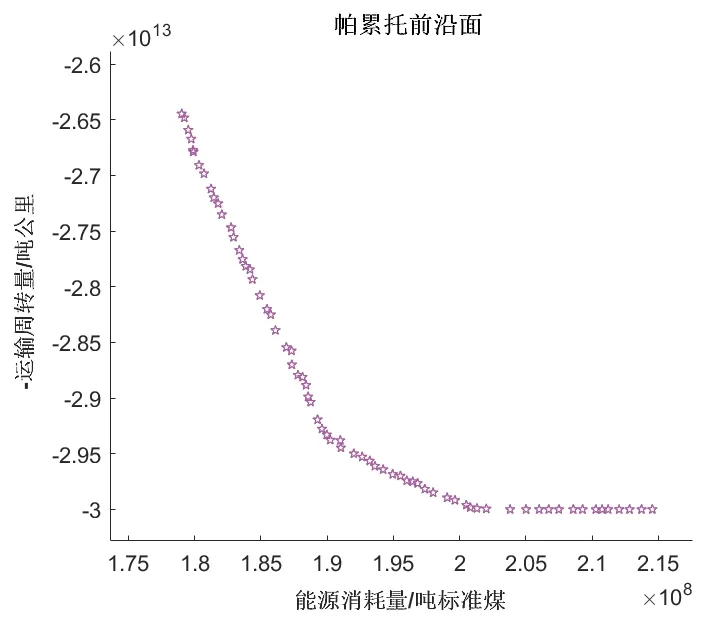
图2 帕累托最优解集结果
2.4.3 决策结果
如表3 所示,本文决策主要分为三种类型,第一种是根据熵权-Topsis 方法计算各方案与最优水平的接近度,得到帕累托解集中与最优水平接近程度最高的前五个解;第二种是优先考虑最低能源消耗量目标;第三种是优先考虑最大运输周转量目标。
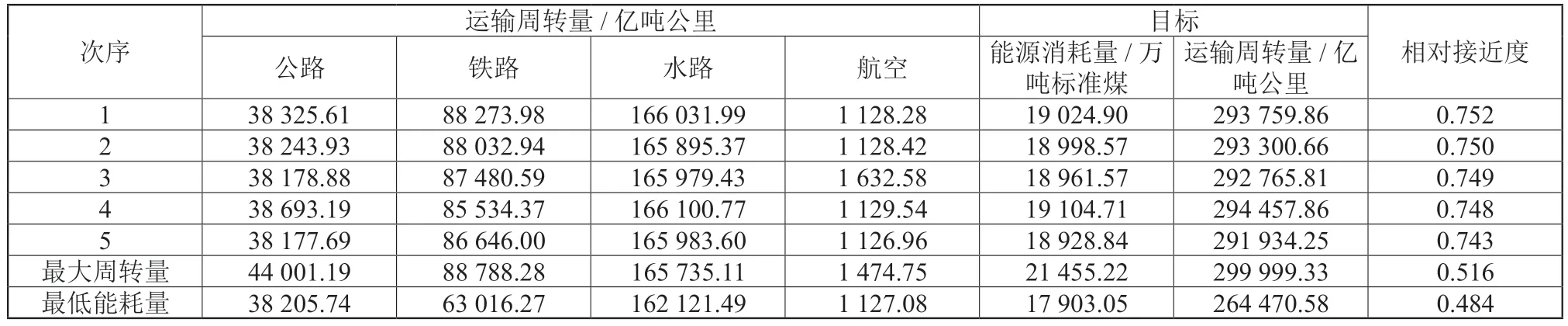
表3 决策得到帕累托最优解集
方案1 与最优水平接近度为0.752,该运输结构相对接近度最高,本文将其作为2030 年碳达峰约束下的最佳运输结构,在该运输结构下,实现293 759.86 亿吨公里运输周转量需消耗19 024.90 万吨标准煤。与此相比,现有运输结构实现同等运输周转量需消耗27 353.09万吨标准煤(表4),优化后的运输,能源消耗降低了30.45%,单位周转量能耗由0.093 吨标准煤/万吨公里下降到0.065 吨标准煤/万吨公里,碳排放由0.23 吨CO2/万吨公里下降到0.18 吨CO2/万吨公里,优化后的运输结构明显优于原来的运输结构。
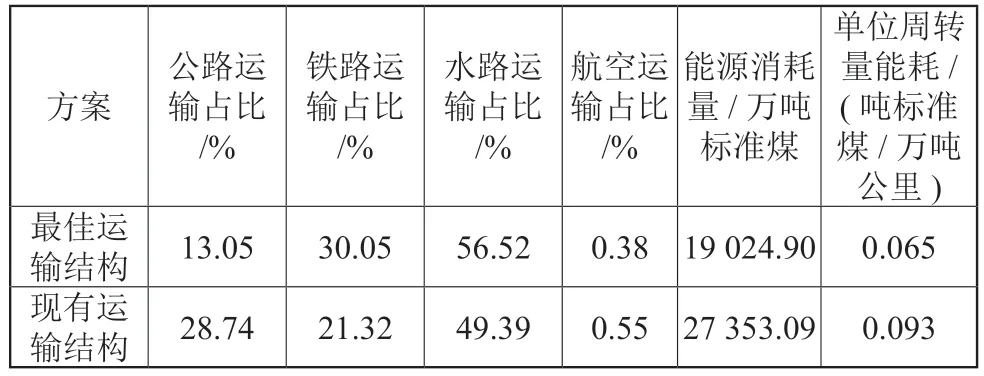
表4 优化前后对比
2.4.4 运输结构优化路径分析
以上分析得到了2030 年碳达峰时的最优运输结构,本小节进一步探讨如何从现有运输结构逐步调整至最优运输结构。为此,基于2.3 节所构建的运输结构优化模型,调整2020—2029 年的相关参数(时变参数Q1、Q2、C、PGDP、E等均做相应的等距插值),基于NSGA2 遗传算法和熵权-Topsis 法确定历年的最优运输结构。因为2020 年以来受到疫情影响,近几年运输结构变动幅度较小,故图3 主要展示疫情前后运输结构变化趋势。由图3 可知,运输结构整体优化路径契合国家“公转铁、公转水”的战略调整方向,优化后交通运输碳排放整体呈现下降趋势。2023—2026 年主要是“公转铁”调整期,公路占比从26.78%降至18.93%,铁路占比则从22.41%升至28.12%;2023—2027 年主要是“公转水”调整期,尤其是2026—2027 年,公路占比进一步降至14.97%,水路占比则升至55.78%;2027—2030 年则是相对平稳的微调期。
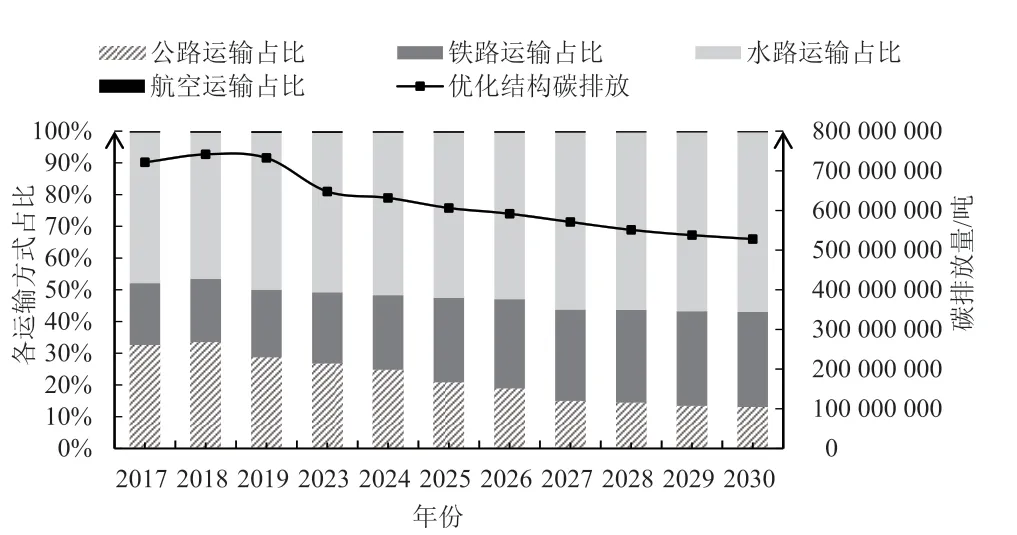
图3 2017—2030年运输结构优化路径
为了早日实现碳达峰,有关部门可以引导现有运输结构朝着优化后的运输结构转变并组织实施交通运输结构性碳减排工程,在重点调整运输结构的领域,加强港口资源整合,鼓励货运企业将货物“散改集”,探索推广“公+铁+水”协同联运模式,依靠创新驱动加快运输结构转变的步伐,解决大宗货物“公转铁、公转水”的现实短板和硬性约束问题。中长距离运输时优先考虑铁路、水路运输,短距离运输时优先采用新能源车辆。
3 研究结论
本文首先运用STIRPAT 模型探究我国交通运输碳排放的影响因素,并以2030 年碳达峰为约束,构建运输结构优化模型,以NSGA2 算法求得帕累托最优解集,并根据熵权-Topsis 法得到最优运输结构,最后将该思路扩展至2020—2029 年得到运输结构优化路径。研究结果表明:2030 年碳达峰时公路、铁路、水运、航空最佳运输周转量占比分别为13.05%、30.05%、56.52%、0.38%,与最优水平接近度为0.752,运输周转量为293 759.86 亿吨公里,能源消耗量为19 024.90 万吨标准煤,同现有运输结构相比降低了30.45%。另外,运输结构整体优化路径显示,2023—2026 年主要是“公转铁”调整期,2023—2027 年主要是“公转水”调整期,2027—2030 年则是相对平稳的微调期。
本文构建的碳达峰约束下运输结构优化模型,不仅给出了我国2030 年的最优运输结构,还提供了从当前运输结构逐步调整至最优运输结构的具体优化路径,对我国交通运输业低碳发展具有一定的参考意义。未来研究还需进一步探讨能源技术进步、多式联运等对低碳运输结构调整策略的影响。

