基于附加改进有源滤波器的柔性直流输电系统高频振荡抑制策略

孙银锋，刘金鑫，梁 栋

（1.现代电力系统仿真控制与绿色能源新技术教育部重点实验室（东北电力大学），吉林吉林 132012；2.国网吉林供电公司，吉林吉林 132001）

0 引言

基于模块化多电平换流器的柔性直流输电技术（Modular Multilevel Converter Based High Voltage Direct Current，MMC-HVDC）凭借其易扩展、谐波含量少、可控性强等方面的优越特性得到了快速发展[1-5]。目前，已有多项工程采用了模块化多电平换流器（Modular Multilevel Converter，MMC）拓扑结构。伴随着换流站电压等级和容量的持续提升，换流站接入方式逐渐转变为主网接入，因此换流站安全可靠运行对交流电网愈发重要[6]。而目前各大柔性直流（柔直）工程中高频振荡现象已经频繁出现[7-9]。例如舟山五端工程的高频分量跳闸现象[10]、厦门工程直流侧550 Hz 振荡[11]、鲁西工程1 270 Hz 以及渝鄂联网工程的700 Hz 和1.8k Hz 的高频振荡[12]。发生高频振荡时，系统的有功、无功损耗将会大大增加，甚至会产生击穿一次设备从而使得系统闭锁停运的严重后果。因此，对MMC-HVDC 高频振荡抑制策略的研究具有重要的实际工程意义。

对于MMC-HVDC 的高频振荡抑制策略的研究，首先应构建适用于高频段分析的MMC 阻抗模型，文献[13-16]建立了高阶的MMC 线性化模型，并研究了内外环控制系统及内部参数对MMC 阻抗特性的影响，但此类文献很少考虑控制链路延时对MMC 高频阻抗模型的建立产生的影响。文献[17]建立了考虑控制链路延时的MMC 高频阻抗模型，最后得出结论：电压前馈环节的控制链路延时是导致MMC 阻抗出现负阻尼性质的原因，而当MMC 阻抗为负阻尼性质而同时交流系统阻抗呈现电容特性的时候，易发生高频振荡现象。

因此改善MMC 的阻抗特性是抑制振荡问题的有效方法，目前改善MMC 阻抗特性的方式一般分为附加无源和有源滤波装置2 种方法。附加无源滤波装置可以阻止特定频率振荡信号通过MMC，但无源滤波装置存在制造成本高、占地面积大等问题[18]。而附加有源滤波装置主要通过改变MMC 内部控制的结构最终达到改善MMC 阻抗特性的目的。由于外环控制只对基频附近的阻抗特性产生影响，所以主要在内环控制中附加有源滤波装置来改善MMC阻抗特性。文献[19-20]分别提出在MMC 电压前馈控制环节附加一阶低通滤波器与带阻滤波器用以抑制高频振荡，设计了滤波器的控制参数，并在实际工程中进行了验证；文献[21]提出了在电压前馈环节和电流比例积分环节分别附加低通滤波器的高频振荡抑制策略；文献[22]总结了4 种在电流内环控制中不同位置依次附加阻尼控制对抑制多个高频振荡频段的优点与缺点。采用附加有源滤波装置的方法虽然能够抑制MMC-HVDC 的特定频段的高频振荡现象，但会使MMC 中低频段阻尼特性进一步恶化，易引发中低频段的振荡现象，因此对于如何抑制柔性直流输电系统高频振荡并且不会引起其它频段振荡的相关研究还有待深入。

鉴于此，本文首先建立简化的MMC 高频等效阻抗模型，根据阻抗分析法分析了MMC-HVDC 高频振荡的产生机理。在此基础上，提出了在内环电压前馈环节投入改进有源滤波器的高频振荡抑制策略，并设计滤波器的各个参数，最后通过仿真验证了所提抑制策略的有效性和可行性。

1 MMC-HVDC高频阻抗模型

1.1 MMC高频阻抗模型

文献[17]对MMC 高频阻抗进行了详细建模，指出锁相环、功率外环、环流抑制以及电流内环正负序独立及解耦控制等控制环节对MMC 高频阻抗特性影响较小。因此，在研究高频振荡抑制策略时可以忽略这些控制环节所带来的影响，采用如图1 所示的简化控制过程分析即可达到目的[18]。其中，L为高压侧等效电感，数值上等于桥臂电抗Larm的一半与变压器漏抗LT之和，Gi为电流内环PI 控制环节，Gd为系统的控制链路延时环节（其表达式为e-sT，其中s为在频域运算，T为延时时间），KNLM为MMC换流器的最近电平逼近调制系数，此处等效为1，Iref为电流内环控制环节的参考值，Iout为交流侧输出电流，VPCC为交流侧并网电压。

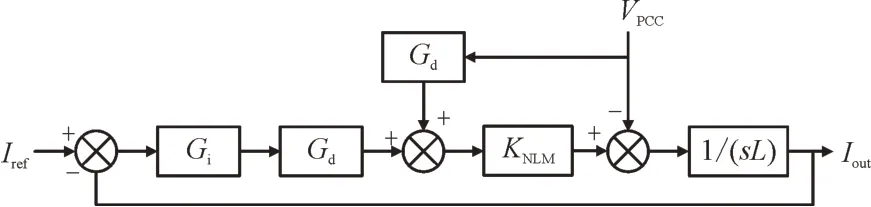
图1 MMC简化控制框图Fig.1 Simplified control block diagram of MMC

根据图1 中VPCC与Iout之间的关系可得到如式（1）所示的MMC 高频阻抗：

式中：ZMMC为MMC 的阻抗。

1.2 交流系统高频阻抗模型

根据文献[18]可知，柔直系统交流部分主要是由输电线路和与输电线路相连的发电机及变压器组成，其中影响高频振荡的主要是输电线路部分。根据文献[23]的分析可知，架空线的频率相关相域模型（Frequency Dependent Phase Model，FDPM）是目前为止适用于高频振荡分析较为精确的模型。但在理论分析中由于FDPM 需要详细的线路结构和参数，在实际工程中很难获取。因此，本文采用分布参数模型进行理论分析[24]，并在建模时考虑电源内阻与变压器漏抗的影响，最后与FDPM 的阻抗扫频曲线进行对比，验证正确性。交流系统具体参数见表1。其中，R0，L0，C0分别为单位长度线路的电阻、电感、电容，l为线路的总长度，Zs为电源内阻，Xt为变压器漏抗，n为π型等值线路级联段总数。

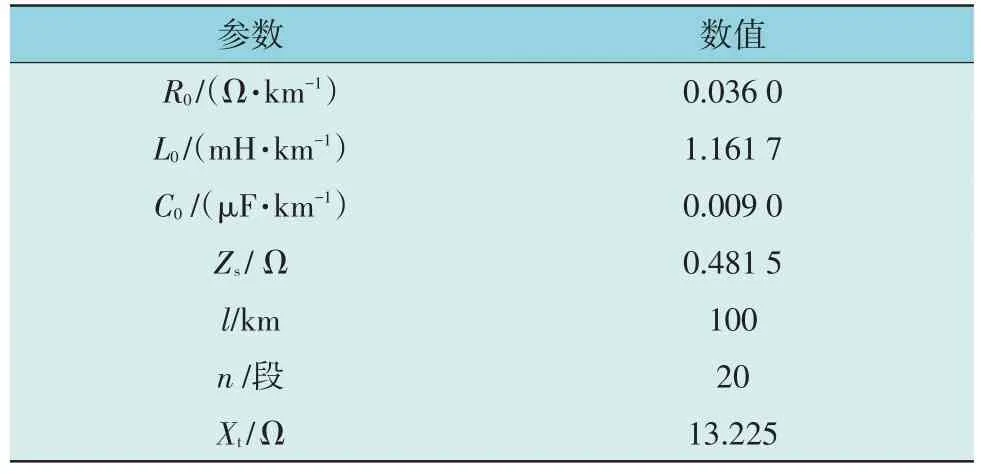
表1 交流系统参数Table 1 Parameters of AC system

图2 为交流线路计算阻抗与扫频阻抗的特性对比，在进行阻抗扫频时，将接入交流线路的电源、变压器等器件均连接在一起。由图2 可知，扫频曲线与计算曲线基本一致，因此可采用分布参数模型进行理论分析。

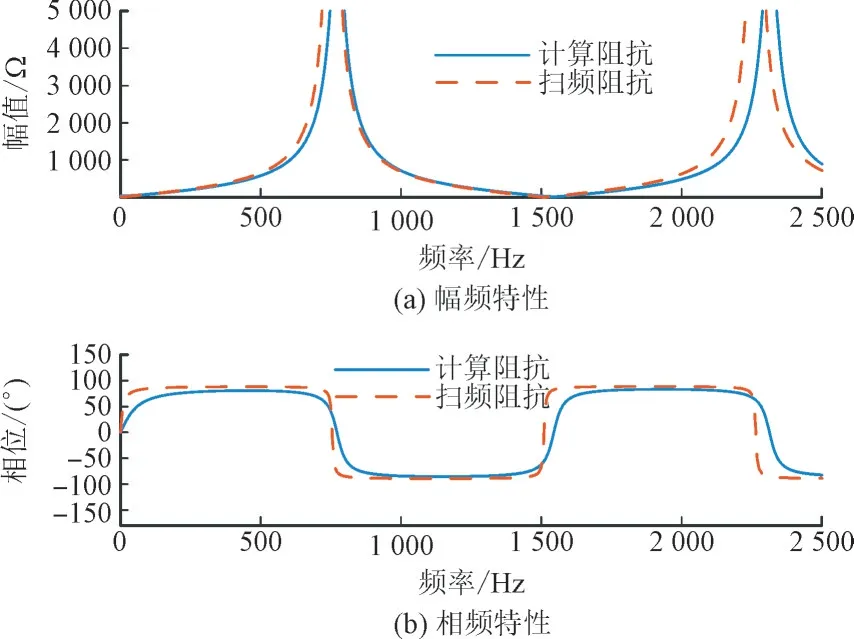
图2 交流线路计算阻抗与扫频阻抗Fig.2 AC line calculation impedance and sweep frequency impedance

2 MMC高频振荡现象

式（1）中，分子项中的sL=2πfL，随着频率f的增加幅值不断增大，远大于GiGd，因此分子的相位主要取决于sL，由此可得MMC 高频阻抗模型的相位表达式如式（2）所示：

式中：∠ZMMC(s)为MMC 的阻抗相位。

根据式（2）可知，MMC 的阻抗相位范围为0°～180°。且在频率f=1处，由180°跳变为0°，在f=1(2T)处为90°，而目前MMC-HVDC 工程中链路控制延时在400～600 μs 之间，本文选择链路控制延时为500 μs。从而得出在1 000 Hz～2 000 Hz 频率范围内，MMC 的阻抗相位大于90°，即表现为负阻尼特性，因此本文设定研究频段截止至2 000 Hz。图3为交流线路计算阻抗与MMC 计算阻抗的对比，表2为MMC 主要参数[25]。

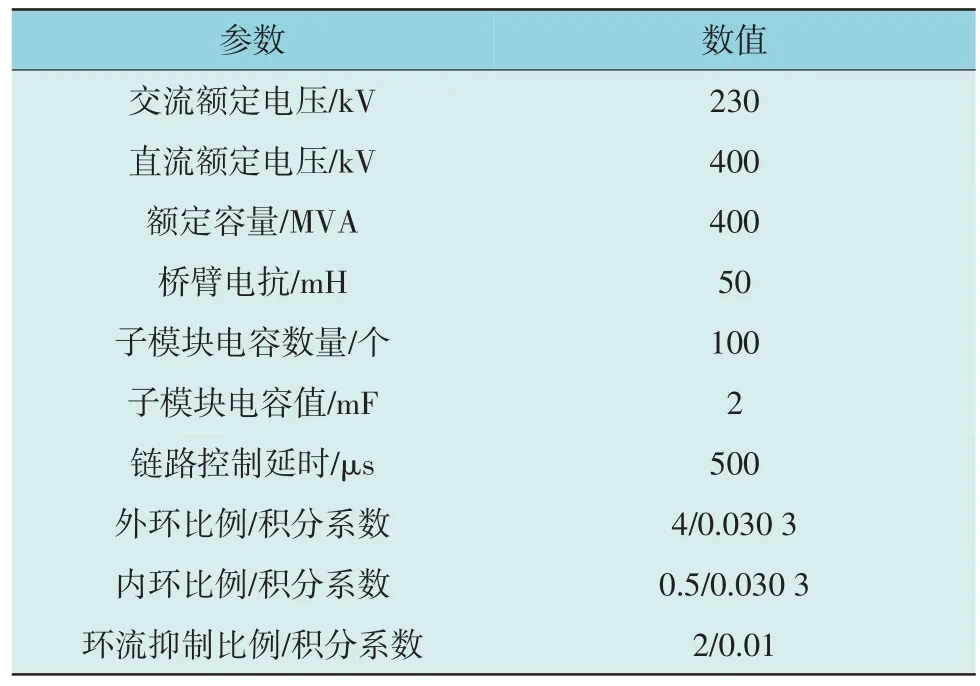
表2 MMC主要参数Table 2 Main parameters of MMC

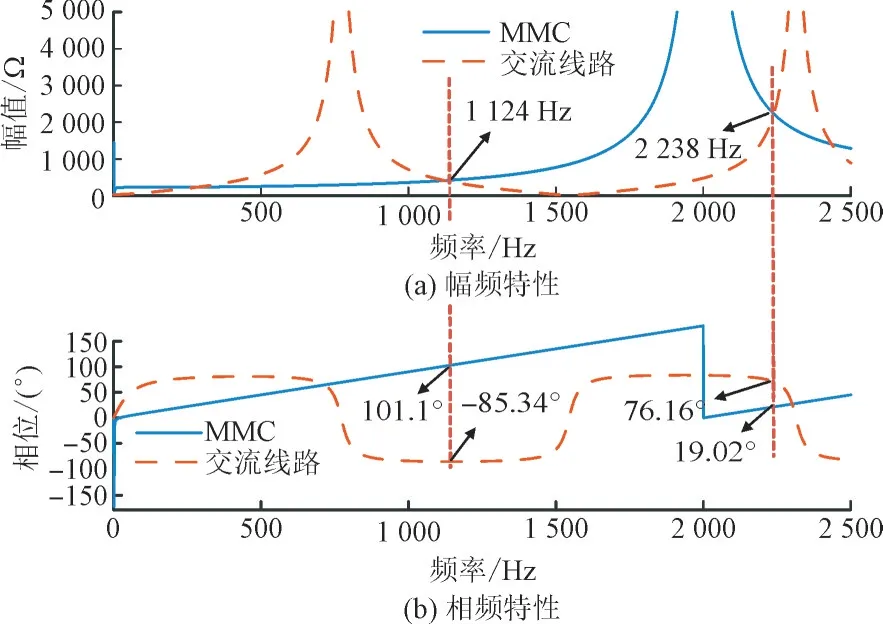
图3 交流线路计算阻抗与MMC计算阻抗Fig.3 Calculated impedance of AC line and MMC

根据奈奎斯特稳定性判据，当满足式（3）时，可判断柔直系统发生振荡现象，振荡频率为MMC 阻抗与交流系统阻抗交点对应的频率。

式中：Zgrid(s) 为输电线路阻抗；∠Zgrid(s) 为输电线路的阻抗相位。

根据图3 可知，MMC 计算阻抗和交流系统阻抗的幅值曲线的交点坐标为1 124 Hz 与2 238 Hz，在1 124 Hz 时二者相位差为186.44°，2 238 Hz 时二者相位差为57.14°，因此MMC 与交流系统之间发生振荡频率为1 124 Hz 的高频振荡现象。

3 附加改进有源滤波器的MMC高频振荡抑制策略

3.1 改进有源滤波器的理论分析

根据第2 节的分析可知，电压前馈环节的控制链路延时是导致MMC 高频振荡现象产生的主要因素。因此本文考虑在电压前馈环节附加高频振荡抑制措施。文献[20]提出在电压前馈控制环节附加带阻滤波器用以抑制高频振荡，但根据文献[21]中的理论分析可知，仅加入一个带阻滤波器并不能彻底抑制高频振荡现象，振荡现象会从高频段向中低频段转移。因此电压与电流会产生中低频段的谐波分量。滤去中低频段的谐波分量首先考虑选用高通滤波器，高通滤波器是能够使大于其截止频率的信号分量无衰减的通过，而对小于截止频率的信号分量大大衰减的器件。然而若选用高通滤波器则会将基频分量也一并滤除，影响系统的稳定性[26]。因此考虑加入低通滤波器。低通滤波器能够使小于其截止频率的信号分量无衰减的通过，而对大于截止频率的信号分量大大衰减的器件。式（4）与式（5）分别为一阶低通滤波器与二阶低通滤波器的传递函数表达式Glf（1）和Glf（2）。

式中：角频率ωn=2πf0，f0为滤波器的中心频率；ξ为滤波器阻尼系数；G为通道增益系数。

设置截止频率为50 Hz，通道增益系数为1。根据式（4）与式（5）可给出两种滤波器阻抗幅值关于频率变化的曲线如图4 所示。

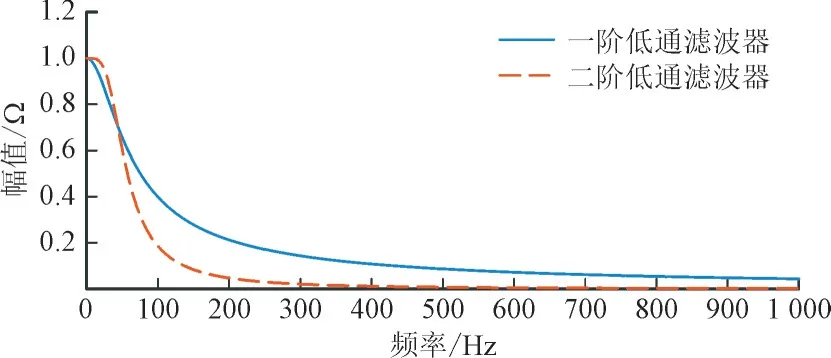
图4 一阶滤波器与二阶滤波器阻抗幅值特性Fig.4 Impedance amplitude characteristics of firstorder filter and second-order filter

根据图4 可知，在相同的截止频率下，二阶低通滤波器相较于一阶低通滤波器从阻带过渡到通带所经历的频段更短，即过渡带更窄，且通带时的阻抗幅值更接近0，因此可以更彻底地滤除谐波。理论上低通滤波器的阶数越高过渡带越窄，然而随着阶数的增加，低通滤波器的成本呈指数增加，综合经济性与性能的要求，选用二阶低通滤波器最为合理。

因此本文提出在带阻滤波器前加入一个二阶低通滤波器，与带阻滤波器共同作用，构成改进有源滤波器，最终达到完全抑制高频振荡现象的效果。此时MMC 的简化控制框图如图5 所示。其中，Gpf为带阻滤波器。

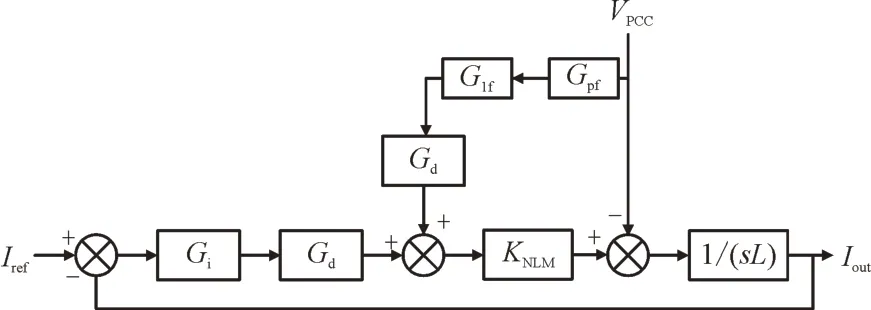
图5 附加改进有源滤波器后的MMC简化控制框图Fig.5 Simplified control block diagram of MMC with improved active filter

典型的带阻滤波器的传递函数如式（6）所示：

此时，MMC 高频阻抗公式为：

3.2 改进有源滤波器的参数设计及可行性验证

首先需要进行带阻滤波器的参数设计，由图3分析得到高频振荡的频率为1 124 Hz，考虑谐波分析的误差，选择带阻滤波器的中心频率f0为1 150 Hz，由于本文中MMC 阻抗出现负阻尼特性的最高频率为2 000 Hz，因此设定上截止频率fup为2 000 Hz，根据式（8）计算得到下截止频率fdown为300 Hz。根据式（9）计算得阻尼系数ξ初始值为1.478。当中心频率确定时，若ξ的值过大，则只能针对特定链路延时产生较好的抑制效果，不具有普适性；若ξ的值过小，可能不会满足相位裕度的要求。因此，本文最终选择ξ的值为1.5。为了尽可能不影响系统的稳定运行，经过多次修正，最终通道增益系数G选择0.7。

然后需要确定二阶低通滤波器的截止频率，分别选取二阶低通滤波器不同截止频率时MMC 计算阻抗的如图6 所示。

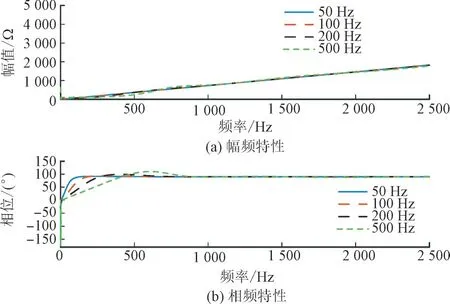
图6 二阶低通滤波器不同截止频率时MMC计算阻抗Fig.6 Calculated impedance of MMC at different cut-off frequencies of second-order low-pass filter

由图6 可知，随着二阶低通滤波器截止频率的降低，MMC 阻抗的负阻尼区域随之减少，当截止频率为50 Hz 时，MMC 阻抗几乎无负阻尼区域，因此二阶低通滤波器的截止频率为50 Hz。

此时投入带阻滤波器与投入改进有源滤波器后MMC 与交流线路的计算阻抗分别如图7 与图8 所示。

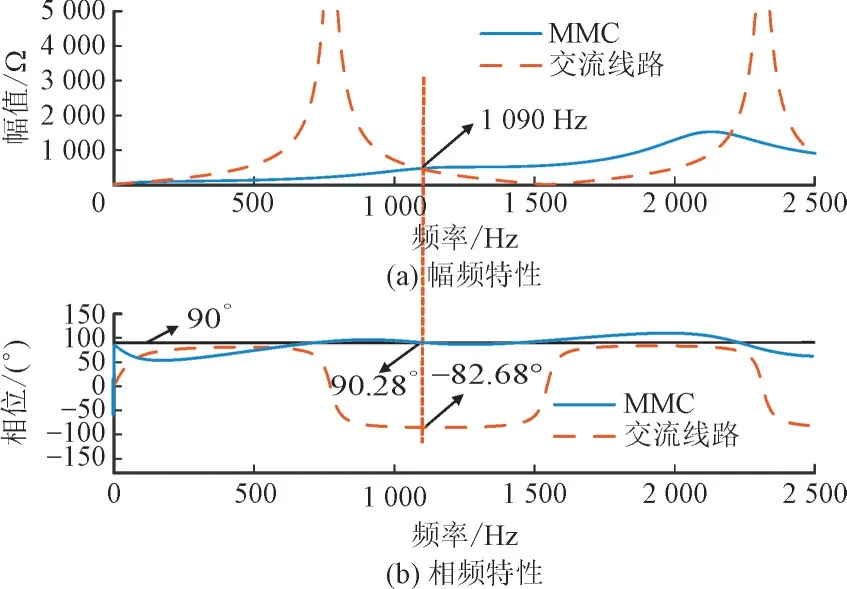
图7 附加带阻滤波器后MMC与交流线路计算阻抗Fig.7 Calculated impedance of MMC and AC line after adding band-stop filter

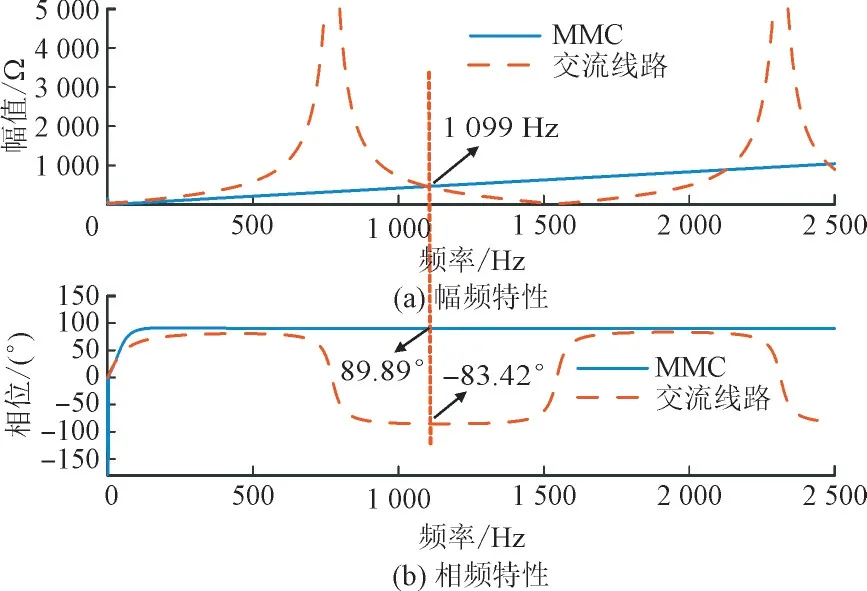
图8 附加改进有源滤波器后MMC与交流线路计算阻抗Fig.8 Calculated impedance of MMC and AC line after adding improved active filter

由图7 可知，投入带阻滤波器后，MMC 的相位曲线在部分频率范围内相位仍大于90°，即MMC 相位仍存在负阻尼区域，当系统运行方式发生变化时，系统仍可能出现新的高频振荡风险。因此仅加入1 个带阻滤波器，不能完全消除可能出现的振荡现象。由图8 可知，投入改进有源滤波器后，二者幅值相等时频率交点为1 099 Hz 处，相位差为173.31°，小于180°，而且观察图8 的MMC 相位曲线可知MMC 的相位完全在90°附近，不存在明显大于90°的区间，即不存在负阻尼频段，抑制了高频振荡现象的同时不会产生其它频段的振荡现象。

为了进一步分析所提抑制策略的有效性，另选取450 μs 和550 μs 2 个典型延时再次从理论上进行分析。图9 和图10 分别为延时450 μs 和550 μs时MMC 与交流线路的计算阻抗，由图9 和图10 得出的结论与图8 几乎相同，因此在延时450 μs 和550 μs 时仍可抑制高频振荡现象的同时不会产生其他频段的振荡。从而可以得出在一定的延时范围内，所提出的高频振荡抑制策略可有效抑制高频振荡现象。

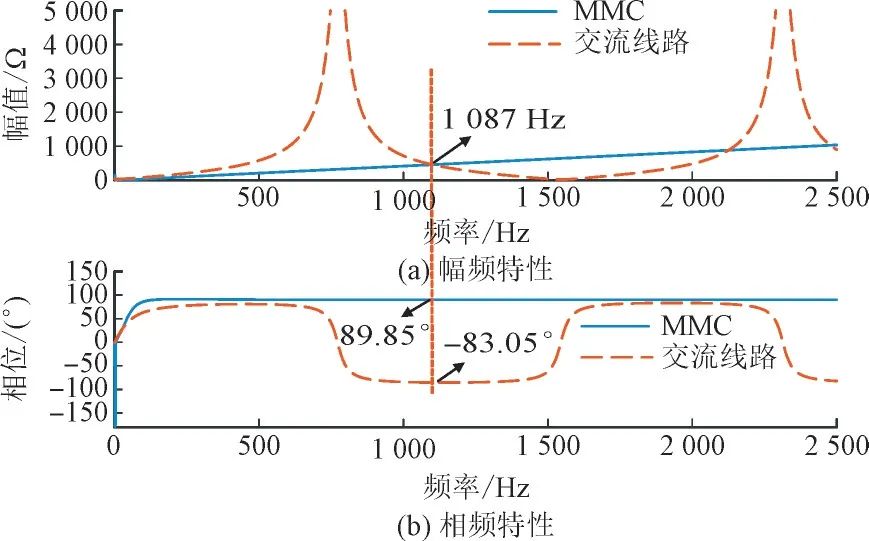
图9 延时450 μs MMC与交流线路计算阻抗Fig.9 Calculated impedance of MMC and AC line with delay time of 450 μs

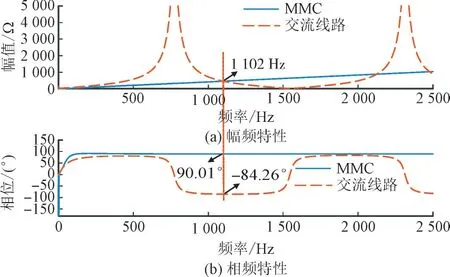
图10 延时550 μs MMC与交流线路计算阻抗Fig.10 Calculated impedance of MMC and AC line with delay time of 550 μs

4 算例分析

4.1 系统稳态特性验证

在PSCAD/EMTDC 中搭建如图11 所示的电磁暂态仿真模型，模型参数如表1 与表2 所示。其中Rg为串联电阻，Lg为串联电感，Cg为并联电容；MMC1采用定有功、无功功率控制，MMC2采用定直流电压与无功功率控制，PCC1和PCC2分别为柔直系统两侧母线。

图11 MMC-HVDC拓扑结构Fig.11 MMC-HVDC topology structure

本节首先验证系统正常运行时投入改进有源滤波器后对系统稳定运行以及MMC 功率控制的影响。图12、图13 分别展示了在2.2 s 时投入改进有源滤波器前后，系统稳态下A 相电压Va和A 相电流Ia的变化过程以及MMC 有功功率P和无功功率Q的变化过程。

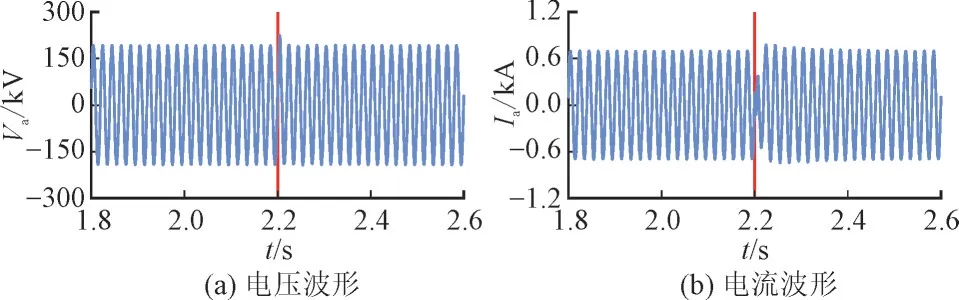
图12 A相电压电流波形Fig.12 A phase voltage and current waveform

图13 MMC功率波形Fig.13 MMC power waveform

由图12 可知，投入改进有源滤波器后，系统交流电压和交流电流几乎无影响，依旧保持稳定运行状态。本文模型中有功功率参考值设置为200 MW，无功功率参考值设置为0 Mvar，由图13 可知，投入改进有源滤波器后，MMC 有功功率和无功功率发生了微小的波动，但在约0.3 s 后功率波形恢复至参考值。MMC 自身很快恢复至正常功率控制状态。因此可以得出结论：投入改进有源滤波器前后，对交流系统稳定运行以及MMC 内部控制过程几乎不会产生影响。

4.2 高频振荡抑制效果验证

本节首先验证在延时为500 μs 的情况下基于投入改进有源滤波器的抑制策略的有效性，并与传统的两种抑制策略进行对比，进一步验证本文所提高频振荡抑制策略的有效性。

在仿真模型中，2 s 时延时从0 μs 变为500 μs，2.2 s 时将带阻滤波器、带阻滤波器与一阶低通滤波器及改进有源滤波器分别投入，投入后的交流系统A 相电压仿真结果如图14（a），14（b）和14（c）所示。2.1 s 时交流系统A 相电压快速傅里叶变换（Fast Fourier Transform，FFT）分析如图14（d）所示。2.5 s时分别投3 种抑制策略后的交流系统A 相电压FFT分析如图14（e），14（f）和14（g）所示。

由图14（d）可知，2.1 s 时A 相电压FFT 分析所得到的振荡频率与图3 得出的结论基本一致。根据图14（a）中电压仿真波形可知，在电压前馈环节仅投入带阻滤波器后系统并未恢复至稳定运行状态。根据图14（e）中的电压FFT 分析可知，系统仍存在主要频率为115 Hz 的谐波，因此仅投入1 个带阻滤波器很难完全抑制高频振荡现象，而是将原本的高频振荡现象转变成中低频振荡，发生振荡转移现象。而在带阻滤波器前加入1 个一阶低通滤波器后，根据图14（b）中的电压仿真波形可知，电压波形得到改善，但是仍然没有达到稳定状态，根据图14（f）中的电压FFT 分析也可看出，谐波含量得到明显降低，但是并没有完全消除。而根据图14（c）可知，投入本文提出的改进有源滤波器并设计该滤波器参数后，系统恢复稳定运行，根据图14（g）中的电压FFT 分析可知，交流系统电压无明显谐波，振荡现象基本消失，MMC 系统恢复稳定运行状态。仿真结果与理论分析基本一致。

为了使结论更具有普适性，本节另选取450 μs和550 μs 2 个典型延时再次仿真验证所提抑制策略的有效性。2 s 时延时从0 μs 分别变为450 μs与550 μs。2.2 s 时将带阻滤波器及改进有源滤波器分别投入后的交流系统A 相电压仿真结果如图15（a）、图15（b）、图16（a）与图16（b）所示。2.1 s 时交流系统A 相电压FFT 分析结果如图15（c）与图16（c）所示。2.5 s 时投入带阻滤波器后的交流系统A 相电压FFT 分析如图15（d）和图16（d）所示。

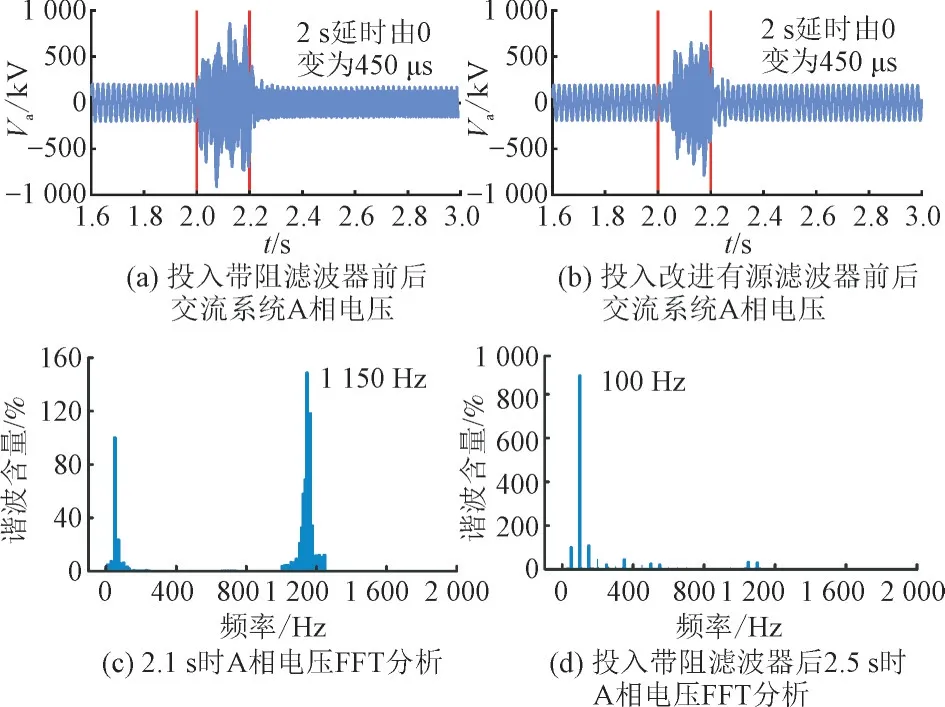
图15 延时450 μs 2种抑制策略电压仿真波形与FFT分析Fig.15 Voltage simulation waveform and FFT analysis of two suppression strategies with delay time of 450 μs

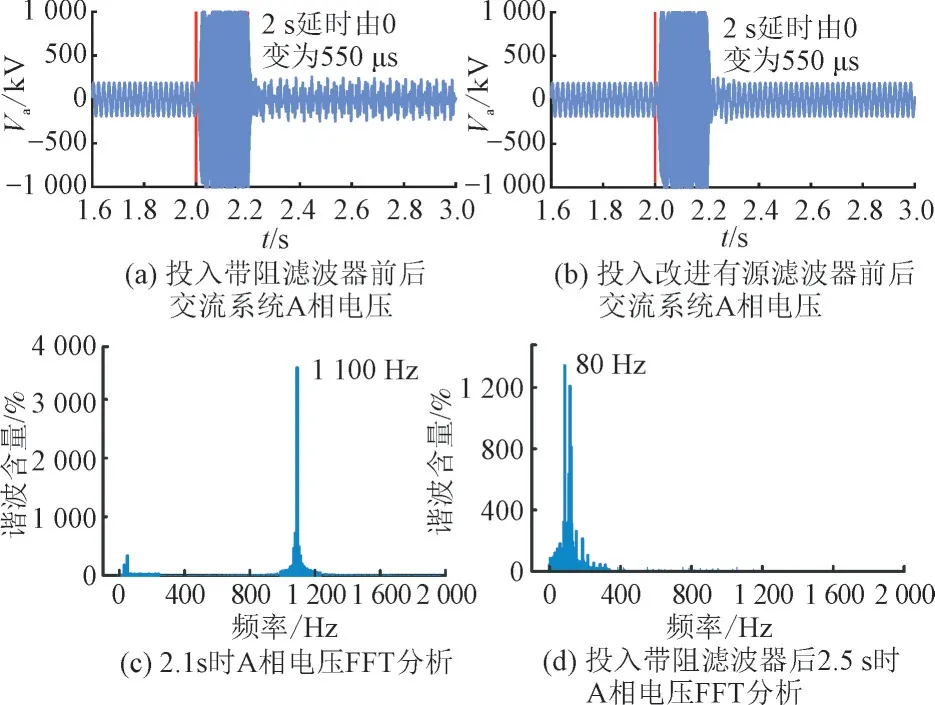
图16 延时550 μs 2种抑制策略电压仿真波形与FFT分析Fig.16 Voltage simulation waveform and FFT analysis of two suppression strategies with delay time of 450 μs

根据图14（d）、图15（c）、图16（c）可知，不同的延时会产生不同的高频振荡频率。根据图15（a）与图16（a）中的电压仿真波形以及图15（c）、图15（d）、图16（c）、图16（d）中的电压FFT 分析可知，在延时为450 μs 与550 μs 2 种场景下，投入带阻滤波器后系统并未恢复至稳定运行状态，电压仍存在频率为100 Hz 附近的谐波，根据图15（b）、图16（b）的电压仿真波形可知，投入本文提出的改进有源滤波器后高频振荡现象基本消失的同时并未产生中低频段的振荡现象，MMC 系统恢复稳定运行状态，进一步验证了本文所提高频振荡抑制策略的有效性与普适性。

综上所述，在考虑MMC 控制链路延时的情况下，在电流内环控制中的电压前馈环节附加改进有源滤波器的高频振荡抑制策略可有效地抑制高频振荡现象的产生，并且解决了附加带阻滤波器的抑制策略中可能会产生的振荡转移现象。本文经过理论分析与仿真结果验证了所提高频振荡抑制策略的有效性以及具有一定的普适性。

5 结论

本文针对主要由MMC 控制链路延时所导致的高频振荡现象，提出了在内环控制中电压前馈控制环节投入改进有源滤波器的高频振荡抑制策略，并通过PSCAD/EMTDC 电磁暂态仿真模型验证了所提出的高频振荡抑制策略的有效性，得到的结论如下所示：

1）不同的链路延时引发的振荡频率不同。

2）所采取的基于改进有源滤波器的高频振荡抑制策略对系统稳态运行特性几乎无影响，且对MMC 本身的功率控制方式几乎无影响。

3）提出的附加改进有源滤波器的高频振荡抑制策略及所设计的改进有源滤波器参数，可有效抑制在典型延时范围内的高频振荡，且不会激发其它频段的振荡现象，提高了柔直系统的稳定裕度。

本文为MMC-HVDC 高频振荡抑制策略研究拓宽了思路，后续将进一步设计基于无源滤波器的高频振荡抑制策略。