基于tGSSA-DELM的短期光伏发电功率预测

杨海柱，李庆华，张 鹏

（1.河南理工大学电气工程与自动化学院，河南焦作 454000；2.天津大学电气自动化与信息工程学院，天津 300072）

0 引言

光伏发电作为主流发电方式之一，在现有的能源结构中起着不可替代的作用。由于光伏发电系统一直处在一个持续变化的环境中，导致光伏发电技术呈现出稳定性差和波动性严重的特性，给光伏并网的电网造成巨大的调节和调度负担。对光伏发电进行可靠的预测对新能源发电的大规模使用和国家电力系统的高质量运行具有重大意义。

目前，短期光伏发电功率预测方法可以归结为两大类：物理模型和智能学习模型。随着技术的发展，智能学习模型也演化出一种组合模型的预测方式。近年来，以人工神经网络[1-3]、支持向量机[4-6]为代表的智能模型已经在光伏发电功率预测方面得到大量研究和利用。王福忠[7]等人使用变分模态分解（Variational Mode Decomposition，VMD）对数据进行分解重构并采用长短期记忆神经网络模型（Neural Network Model For Long And Short Term Memory，LSTM）进行短期形式的光伏功率预测，利用VMD 虽然在一定程度上改善了LSTM 模型的预测精度，但是并没有采取参数寻优的处理方法。袁建华[8]等人考虑原始数据的质量和反向传播（Back Propagation，BP）神经网络的参数对预测效果的问题，在利用VMD 对原始所有数据进行分解后，针对每个分量采用粒子群算法（Particle Swarm Optimization，PSO）进行参数优化后的BP 神经网络模型进行预测，但是并没有解决神经网络在光伏预测方面中预测速度慢的问题。朱瑞金[9]等人使用互补集合经验模态分解（Complementary Ensemble Empirical Mode Decomposition，CEEMD）和排列熵优化最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）的组合模型，综合考虑了模型的预测效率和精度，但是通过添加噪声的方式并没有解决向量机模型受数据影响大和参数调整困难的现状。深度极限学习机（Deep Limit Learning Machine，DELM）作为一种新型人工智能预测模型，它在极限学习机（Limit Learning Machine，ELM）的基础上进行改进，引入自动编码器的极限学习机（Extreme Learning Machine for Automatic Encoders，ELM-AE）进行隐藏层输入权重和阈值初始化，有效克服了ELM 因随机产生权值和阈值而导致输出不稳定的问题[10]，同时也克服了神经网络等模型的训练速度慢，预测时间长的弊端。李斌[11]等人利用遗传算对ELM 进行参数寻优并用于光伏发电功率预测，在预测精度上有了一定提升。王瑞[12]等人验证了利用智能算法改进混合极限学习机在风功率预测方面的有效性。王忠义[13]等人利用非洲秃鹫优化算法对DELM 参数进行寻优，取得了不错的预测效果。

本文结合深度极限学习机的参数少、预测速度快的优势，提出一种基于皮尔逊相关性、麻雀算法（Sparrow Search Algorithm，SSA）、深度极限学习机的短期光伏发电功率预测，采用SSA 对DELM 的相关参数进行寻优，建立改进麻雀优化深度极限学习机的光伏发电功率预测模型，用每个季节的一天数据对模型的高精准度和通用性进行验证。

1 光伏发电功率特性分析

1.1 光伏出力影响因素分析

对于一个特定的光伏站来说，影响光伏出力的因素主要有光辐照度、散射、温度、相对湿度、风速、风向等，其中最为主要的是光辐照度（水平辐射），理论中对光伏发电功率的高精度预测要考虑所有影响因素，但是各类天气因素对光伏发电功率的影响程度不同，若将所有因素考虑在内将造成预测的冗余和偏差。因此根据光伏发电的特点，本文采用皮尔逊相关法对天气因素进行筛选，确定出模型输入向量。

1.2 相关性分析

光伏发电是一种受多种因素影响的发电方式，在预测过程中，若考虑所有的影响因素，将会给预测带来冗余和预测耗时问题，甚至为预测的期望造成相反的后果，因此，利用皮尔逊对影响功率的天气因素进行筛选，确定关键影响因素，其表达式为：

式中：ρx,y为皮尔逊相关系数，取值范围为[-1,1]，当取值为-1 时，表示变量间完全负相关的关系，+1 时表示完全正相关的关系，0 表示两变量间不存在线性相关；n为样本数；xi，yi分别为天气因素和光伏发电功率；为xi，yi两个变量的平均值。

相关系数取值范围常常被用以判断变量之间的相关强度，相关程度按绝对值大小分类如表1 所示。

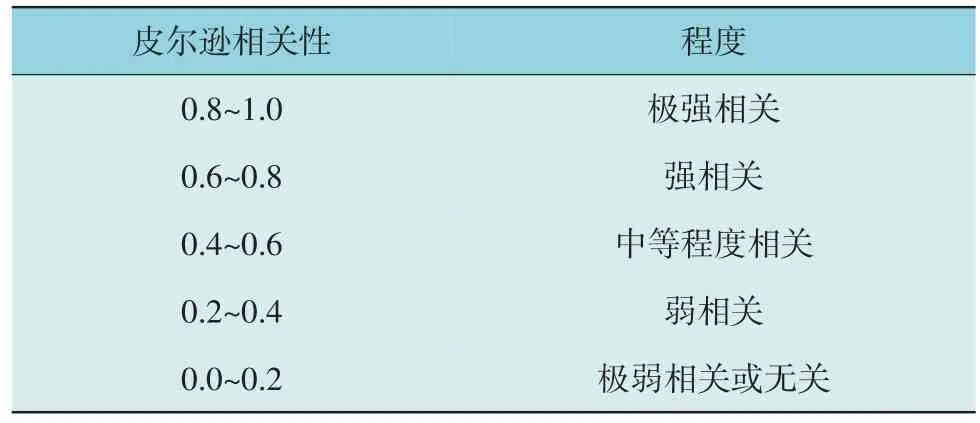
表1 皮尔逊相关性分类Table 1 Classification of Pearson correlation analysis

使用澳大利亚某光伏电站数据进行相关性分析，其中考虑的气象因素包含光水平辐射度、散射、温度、相对湿度、风速、风向、降水量。由于变量之间的量纲不同会对预测过程产生影响，所以在进行相关性分析前对原始数据进行归一化处理：

式中：zi为第i列的原始数据；zi,min为第i列数据的最小值；zi,max为第i列数据的最大值。

气象因素和光伏发电功率之间的相关性如表2所示。

由表2 可知风向、降水量的相关系数值分别为-0.050 8 和-0.0636，几乎没有相关性，因此将水平辐射、漫射、温度、相对湿度和风速5 个相关性较强的气象因素作为输入特征。

2 模型相关原理

2.1 传统麻雀算法

麻雀算法（SSA）是XueJ[14]等在2020 年提出的一种群智能寻优算法。根据麻雀觅食的特点，将SSA 中麻雀种群分为发现者、加入者和警戒者3 部分[15]。假设SSA 中麻雀的个体数量为N，则种群X可以表示为：

式中：m为变量的维数。

其适应值Fx可以描述为:

式中：f(xN,m)为麻雀个体的适应度值；Fx为求取麻雀种群适应度值的函数。

在SSA 中，发现者在整个种群中起到领导者的作用，通常在种群中具有10%～20%的占比[16-17]。

1）发现者的位置更新可以描述为：

2）加入者的位置更新过程可以描述为：

3）为了觅食的安全性，需要设置10%～20%的麻雀作为警戒者[18]。警戒者位置更新公式为：

2.2 改进的麻雀算法

由于群智能算法本身的一些特性，给算法造成全局搜索能力差而过早进行收敛，产生局部最优的现象。因此，本文对传统SSA 做如下改进。

1）黄金正弦算法

黄金正弦算法（Golden-SA）利用正弦函数的黄金分割系数和独特的寻优特点，使SSA 既能对局部进行充分搜索又能很好地开展局部开发[19]。根据发现者在觅食过程中位置变化可知，算法在迭代初期就呈现出陷入局部最优的趋势，出现过早收敛的问题，因此本文使用Golden-SA 对发现者在觅食过程中的移动方式进行改进，此时，发现者位置为：

式中：Z1为取值[0,2π]的随机数，其决定个体移动的距离；Z2为取值[0,π]的随机数，用于决定下次更新位置的方向；x1，x2为通过黄金分割原理得到的系数，且x1=-π+(1-τ)×2π，x2=-π+τ×2π，其中。

2）自适应t分布和动态选择策略

t分布存在标准高斯分布和柯西分布2 个边界特例[20]。本文在个体位置更新方式中以迭代次数iter作为t 分布变异算子，对麻雀位置起到扰动作用[21]。具体更新公式为：

虽然自适应t分布的引入对于避免陷入局部最优具有很好的调节作用，但将这种改进方式对所有麻雀均使用，在一定程度上会摒弃了传统SSA 的特性，并且还会造成效率低，产生耗时问题。动态选择概率P的引入则避免了此问题的发生[22]。

式中：maxiter为最大迭代次数；ω1为决定动态选择的概率上限；ω2为决定动态选择概率的变化幅度。

改进后的麻雀算法流程如图1 所示。

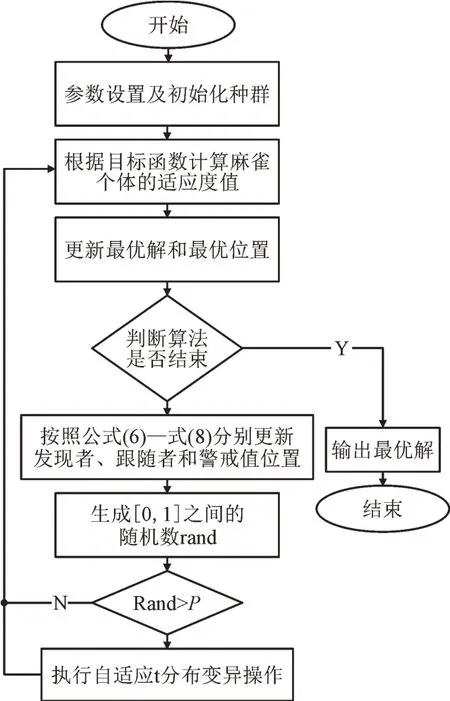
图1 改进的麻雀算法流程Fig.1 Improved sparrow algorithm flow

2.3 深度极限学习机

Huang 等人在2004 年提出的一种被称为极限学习机的快速学习模型，ELM 网络相比于其他类别的模型具有学习速度快、泛化能力强等优点[23]。自动编码器（AE）是作为一种无监督学习算法，在DELM 模型中最为逼近器使用，其在DELM 中发挥着将ELM 的输入用于输出的作用[24-25]。

结合ELM 和AE 的深度极限学习机（DELM）的分层无监督训练方式，对于重构误差具有很好的衰减作用[26]。图2 为DELM 模型的训练过程，其中，β为输出权重，β=[β1,β2,…,βn],βi(i=1,2,…,n)。ω为输入权重，ω=[ω1,ω2,…,ωn],ωi(i=1,2,…,n)，X1，X2，Y分别表示各隐藏层输出，T为输出层输出。

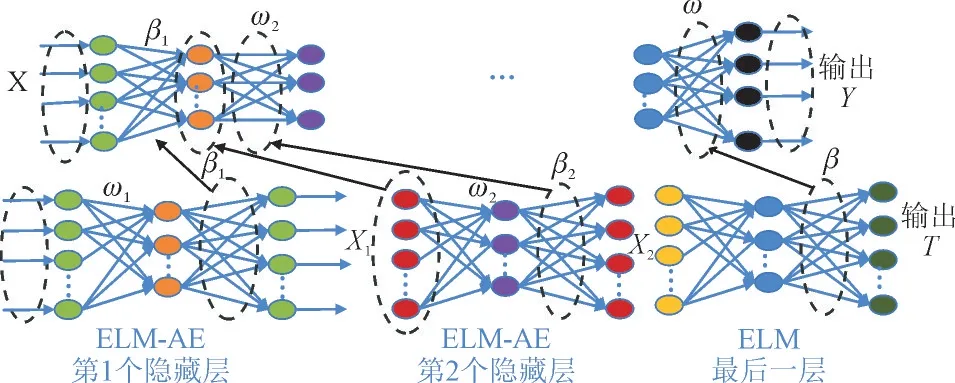
图2 DELM模型训练过程图Fig.2 Diagram showing DELM model training process

DELM 隐藏层的输出权重可以表达为：

式中：I为单位矩阵；X为输入数据，X=[x1,…,xN]；C为正则化参数；H为隐藏层输出。

对于等维度特征表达，隐藏层的输出权重可以表示为：

2.4 tGSSA-DELM模型的建立

在DELM 的模型训练过程中，采用黄金正弦算法和自适应t 分布和动态选择策略改进后的麻雀算法tGSSA 对输入层权重和阈值进行参数寻优，可以得到最优输入层权重和阈值，减小DELM 的波动问题。整个优化流程如图3 所示。

图3 tGSSA-DELM流程图Fig.3 Flowchart for tGSSA-DEM

3 仿真测试

本文采用tGSSA-DELM 模型对未来1 d 的光伏站发电功率进行预测。为测试本文所提模型在光伏发电功率预测领域的应用性能，选用澳大利亚某光伏电站2014 年全年的公开发电数据进行测试，数据采样时间为当地每天8：00—17：30，每隔5 min 进行一次采样。选用2014 年10 月、1 月、4月、7 月来进行四季模拟，取每月中的28 天共3 220个样本，其中前3 105 个样本点为训练数据集，后115 个样本点为预测数据集，通过本文所提模型进行光伏站全天（8：00—17：30）的功率预测分析。

3.1 评价指标

为了对各模型的预测性能进行更加全面的评估，本文选用均方根误差（Root Mean Squared Error，RMSE）、平均绝对误差（MeanAbsolute Error,MAE）、平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）、拟合优度(R2)作为评价指标进行误差分析。RMSE，MAE，MAPE 的值分别用ERMS，EMA，EMAP表示，表达式为：

式中：pi为光伏发电功率真实值；为光伏发电功率预测值。

3.2 算例分析

3.2.1 算法模型测试

为更加直观表现麻雀算法改进后的优越性能，通过单峰和多峰测试函数进行收敛速度、精度和全局寻优比较试验，试验测试条件为：种群数量为30，迭代次数为300。测试函数如式（17）所示。

改进前后的麻雀算法对比如图4 所示。

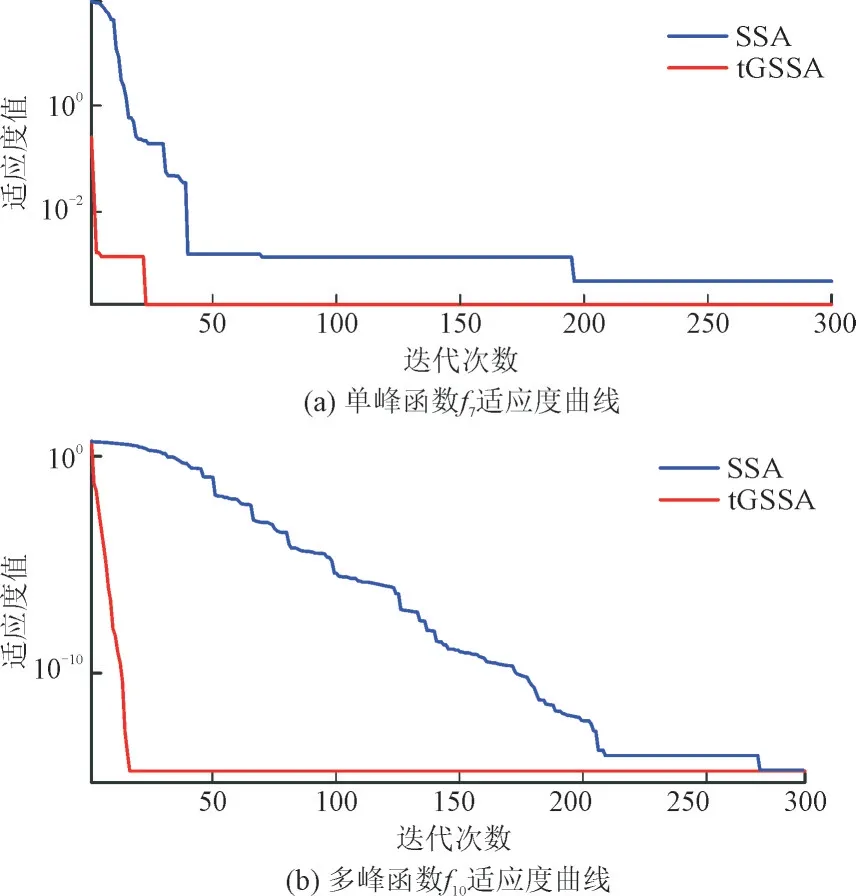
图4 2种函数下的适应度曲线Fig.4 Fitness curves with two functions

由图4 可知，在单峰、多峰测试函数下SSA 在300 次迭代结束后均未达到理想最优结果。tGSSA在迭代50 次前均已达到全局最优值，且收敛速度快。表明tGSSA 性能远超传统SSA 的性能。

为验证本文所提DELM 模型在利用算法提高预测精度时，依然保持在高效率进行光伏功率预测方面的优越性，本文将麻雀算法优化深度极限学习机（Sparrow Algorithm Optimization Deep Limit Learning Machine，SSA-DELM）分别与在光伏预测中常用的SSA 优化的BP 神经网络模型和LSSVM 向量机模型进行预测性能对比，模型参种群数量为20，迭代次数为100，预测时间对比如表3 所示。

表3 3种预测模型预测时间对比Table 3 Comparison of prediction time among three prediction models s

由表3 可知，在相同条件下，DELM 模型在保证预测精度的情况下可以明显提高预测的速度，可以看出在同样的算法优化条件下，DELM 模型在预测速度方面存在明显的优势。

3.2.2 预测结果分析

为了更加直观看出本文所提模型在光伏发电功率预测技术中的有效性和优越性，选取DELM，SSA-DELM 典型模型和遗传算法优化深度极限学习机（Genetic Algorithm Optimization of Deep Limit Learning Machine，GA-DELM）、人工蜂群算法优化深度极限学习机（Optimization of deep limit learning machine using artificial bee colony algorithm，ABCDELM）、鲸鱼优化算法优化深度极限学习机（Whale algorithm optimization deep limit learning machine，WOA-DELM）与其进行比较。对于DELM 模型采用sig 激活函数，隐藏层数设置为2，每层节点数为3。

由图5 可以看出，春季预测值跟随真实值呈现出较大的波动性，存在很明显的随机性，且本文所提模型和其他对比模型得到的功率拟合曲线与实际曲线均有较大的差距。但是相比而言，改进的tGSSA-DELM 模型得到的功率拟合曲线要优于其他对比模型。

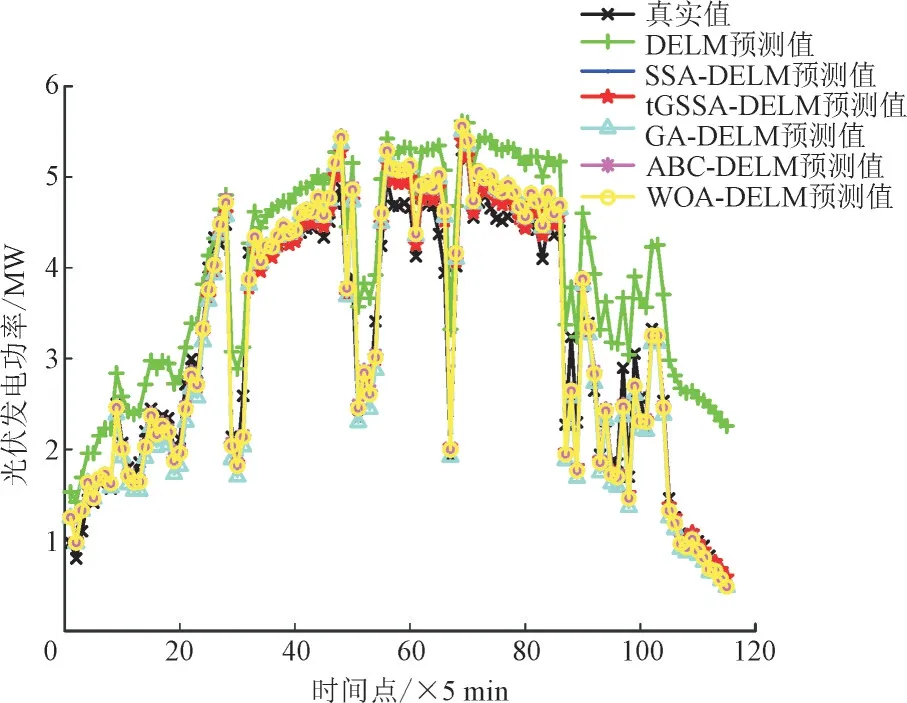
图5 春季预测结果Fig.5 Forecasting results in spring

由图6 可以看出，夏季的预测曲线和真实光伏功率曲线波动均较为稳定，利用tGSSA 与DELM 组合预测模型拟合效果要优于传统模型和其他对比算法。

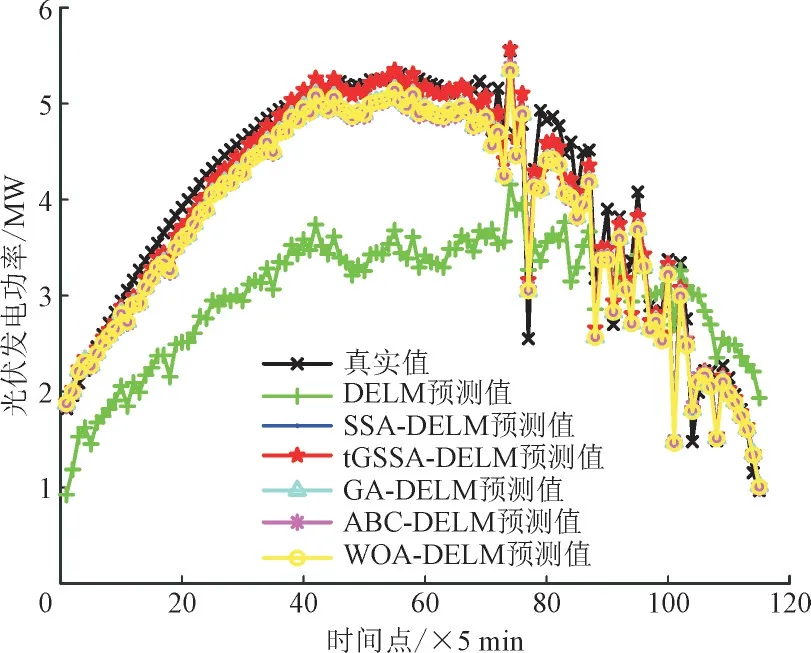
图6 夏季预测结果Fig.6 Forecasting results in summer

由图7 可以看出，不同模型得到的功率拟合曲线均比较稳定且十分接近实际功率曲线，由此说明，不同模型对于秋季的光伏发电功率适应性较好。

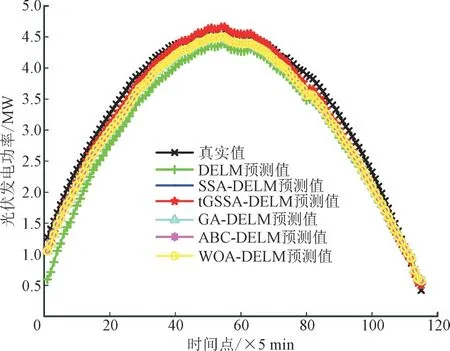
图7 秋季预测结果Fig.7 Forecasting results in autumn

由图8 可以看出，传统DELM 模型拟合曲线与实际有很大偏差，并且各个模型在中午时刻与实际有明显的偏差，但是相比而言，本文所提模型拟合度更高，tGSSA-DELM 模型具有更强的预测性能。

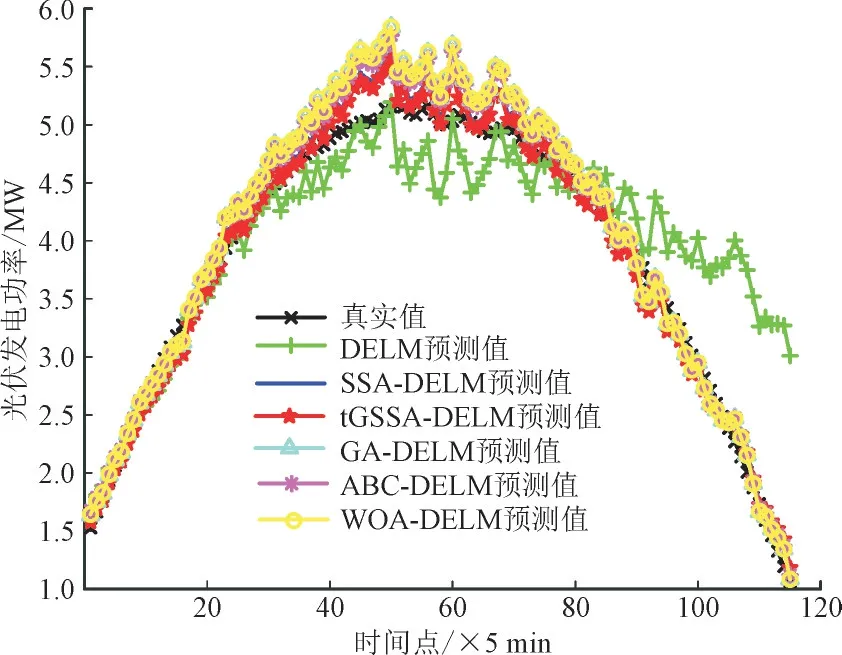
图8 冬季预测结果Fig.8 Forecasting results in autumn

表4 为不同预测模型在不同季节环境下的预测评价指标对比结果。表4 给出了春季、夏季、秋季、冬季4 个季节在6 种预测模型下的对比结果。由表4 可知，6 种模型均可以对不同季节的光伏发电功率做出有效的预测，但相比之下，tGSSA-DELM得到的预测效果要优于传统的DELM，SSADELM。而对于GA-DELM，ABC-DELM，WOADELM 来说，tGSSA-DELM 具有更小的预测误差，tGSSA-DELM 预测模型在春季、夏季、秋季、冬季下的RMSE 值分别为0.213 92，0.189 19，0.147 77，0.150 06，MAE 值分别为0.158 65，0.139 67，0.130 14，0.115 96，MAPE 值分别为5.911 1%，4.03 36%，4.900 7%，3.353 4%，相关系数R2分别为0.938 08，0.954 52，0.958 11，0.962 85。以春季为例分析，本文提出的模型相比于DELM，SSA-DELM 模型R2分别提升了0.191 67，0.010 8，相比于GA，ABC，WOA优化后的模型，拟合优度R2分别提升了0.018 78，0.012 57，0.014 02。

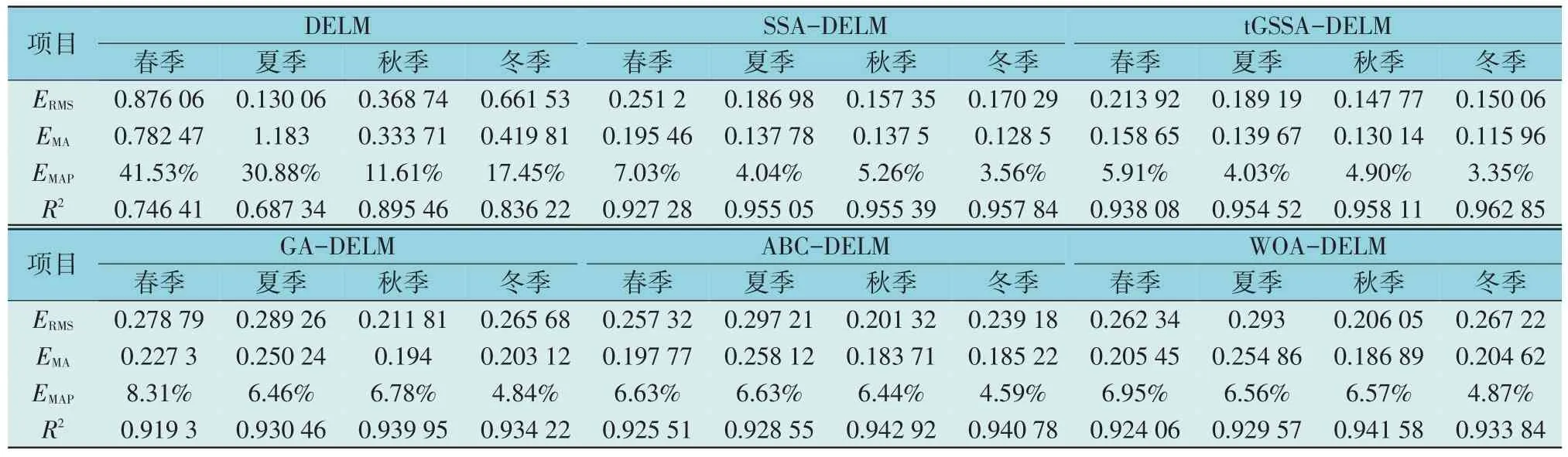
表4 不同季节下的预测模型仿真性能指标对比Table 4 Comparison of simulation performance indicators among prediction models under different seasons

分析可知，对于4 个季节下的预测，本文模型具有较好的预测性能，并且夏季、秋季、冬季的光伏发电预测精度要明显优于春季的预测结果，这是由于春季的发电功率存在较强的不稳定性和波动性，且春季为多雨季节，空气湿度高，给预测带来了较大的困难，而其他3 个季节的光伏发电功率较为稳定，光照充足，降水天气少，因此预测模型在夏季、秋季、冬季下的适应性要强于春季。由不同季节下各模型的预测效果对比可知，tGSSA-DELM 预测模型在光伏发电功率方面具有较高的预测精度，在不同季节下的预测精度都在90%以上，具有较高的实用性和推广意义。

4 结论

为了提高短期光伏发电功率的预测性能，提出一种基于tGSSA-DELM 的短期光伏发电功率预测模型，通过实例得到如下结论：

1）针对现有光伏预测模型因需优化参数多而导致的预测速度低、泛化能力弱的问题，提出了基于DELM 的光伏发电功率预测模型。

2）针对DELM 因输入权重偏置选择不当而导致的预测性能低下的问题，提出了tGSSA 用于优化DELM 的相关参数，结果表明，tGSSA 可以寻得更优的DELM 相关参数解，且能够有效提高其整体预测性能。

3）仿真结果表明，tGSSA-DELM 模型能够有效对短期光伏发电功率做出预测，在预测速度方面具有极大的优势，且在4 个季节下得到的4 个评价指标均优于其他模型，但是该模型在夏季的预测精度相比于其他四个季节的预测精度低，是下一步研究和改进的重点问题。