Capurability analysis for arbitrarily high-speed maneuvering targets

Shoo WANG, Yng GUO,*, Shicheng WANG, Lixin WANG,Ynhu TAO, Zhengfei PENG

a Xi’an Research Institution of Hi-Technology, Xi’an 710025, China

b Xi’an Satellite Control Center, Xi’an 710043, China

KEYWORDS

Abstract The capturability of an arbitrarily maneuvering target featuring speed superiority over an interceptor is analyzed for Augmented Pure Proportional Navigation (APPN) and Retro-Augmented Proportional Navigation (RAPN) guidance.This paper focuses on intercepting arbitrary maneuvers to study more general interception problems.A comparative analysis of the capture region between head-on interception related to APPN and head-pursuit interception related to RAPN is proposed.The results indicate that RAPN performs better than APPN in capturability.It is concluded that increasing the target velocity, which increases the velocity ratio, significantly weakens the capturability of the interceptor, and the average acceleration and relative distance affect the location of the capture region but not its size.The analysis is based on prior knowledge of the target maneuver, which inevitably leads to deviations from actual maneuvers in practical engagement, so a deviation analysis is implemented.The effective capture region shrinks as the absolute value of acceleration deviation increases, and the RAPN has a better deviation fault tolerance compared with the APPN.The results reveal that a larger relative distance can weaken the deviation fault tolerance, and the target velocity has opposite effects on head-on and head-pursuit interception.

1.Introduction

Pure Proportional Navigation (PPN)1–3guidance law, as a major variant of the Proportional Navigation (PN) guidance law, has been analyzed extensively in the literature.The True Proportional Navigation (TPN) guidance laws,4,5with lateral acceleration normal to the Line-of-Sight (LOS), are another major variant of the PN guidance laws.Unlike TPN,PPN lateral acceleration is applied normal to the interceptor’s velocity vector.The LOS rate item in PPN’s analytical acceleration expression is the only quantity that needs to be measured in the implementation process and is readily available from the interceptor’s Infrared (IR) sensor.Because of its robustness and practicality, PPN outperforms TPN guidance laws in applications.6The class of Generalized Proportional Navigation (GPN) laws was firstly proposed in Ref.7.The results manifested that GPN was superior to TPN with a larger capture region and a shorter interception time.The only work on the derivation of closed-form analytical solutions for PPN was presented by Becker,2and the closed-form analytical solution on TPN, realistic TPN, and Generalization of TPN(GTPN) were presented in Refs.4, 8, and 9 respectively.Although a modification to GTPN 9 was conducted to achieve being almost comparable to PPN in capture zone, in general,the capturability of PPN was found to be better than that of all forms of TPN.10A general study of several variants of PN guidance was done by Yang CD and Yang CC,11and then its extension to 3D PN guidance law was analyzed in Ref.12

Guelman first studied PPN against a non-maneuvering target,1and then presented sufficient conditions on the capturability against a target executing constant maneuver, and at the same time,some results on the interceptor lateral acceleration requirement were obtained.13The capturability for a maneuvering target executing bounded piecewise continuous time-varying maneuver was analyzed by Ghawghawe and Ghose14using Guelman’s approach.The capturability of an arbitrary target with time-varying normal acceleration using three-dimensional (3-D) PPN was studied by introducing a Lyapunov-like approach.15,16Shin and Li17improved 3-D PPN performance by properly selecting the guidance command direction.The Ideal Proportional Navigation (IPN)which used the relative velocity as the referenced direction of interceptor was studied by Yuan and Chern.18According to the closed-form solutions of IPN, the capture criterion of IPN was only related to the navigation constant.IPN was found to be superior to any other PN laws on capturability in the premise of more energy consumption.Using a line-ofsight fixed natural coordinate and three modified polar variables, Tyan19obtained capture zone of General Ideal Proportional Navigation (GIPN) guidance law.However, these studies generally assume a low-speed target or that the interceptor speed is higher than the target speed.The interception of a higher-speed target using PPN was studied by Tyan and Shen.20,21

The two collision conditions for interception of a nonmaneuvering target with higher velocity using PPN are Head-On (HO) and Head-Pursuit (HP) interception.Most existing guidance laws focus on HO interception,which is generally designed for the interception of lower-speed targets.When this guidance law is used to engage a higher-speed target, there is a larger closing velocity between the interceptor and target, and the capturability deteriorates significantly.

Compared with guidance laws based on HO interception,those based on HP interception are designed to intercept high-speed targets.As presented by Golan and Shima,22HP interception places the interceptor ahead of the target on its flight trajectory, so the closing velocity is reduced.Ge et al.23extended the HP interception to a 3-D nonlinear variable space using Lyapunov stability theory.Prasanna and Ghose6described an HP interception guidance law named Retro Proportional Navigation (RPN) that uses a negative navigation constant.Analysis of the RPN against a non-maneuvering target with higher constant speed than interceptor manifests that,even though more time is consumed by RPN to intercept the target successfully than by PN, the interception performance of the RPN is better than that of the PN, in terms of capturability, lateral acceleration, and closing velocity.However, the RPN capturability analysis was only implemented for nonmaneuvering targets.Ghosh et al.24proposed a Composite PN (CPN) guidance law that both PPN and RPN guidance laws are used in a 3-D engagement scenario against higherspeed non-maneuvering targets based on the initial situation and terminal impact angle.Ghosh and Ghose augmented RPN in 3-D engagement and presented a nontrivial RPN target capture zone.The concept of Augmented Proportional Navigation(APN)was proposed to solve the problem of intercepting a maneuvering target in Refs.23–26.

Augmented Pure Proportional Navigation (APPN), as a variation of the PPN guidance law, was presented to account for target maneuvers and the capturability analysis for it was given.Sufficient conditions for speed ratio, navigation gain,and constraint of lateral acceleration were obtained for targets executing piecewise continuous maneuvers in time.27However,only the situation in which the interceptor’s speed is higher than the target’s speed was considered.The capturability research for high-speed maneuvering targets is still lacking.

Motivated by the RPN which has good performance in intercepting high-speed targets, and the APPN which is suitable for intercepting a maneuvering target, Retro-Augmented Proportional Navigation (RAPN) comprising these two guidance laws was presented by Sun et al.28Although the capturability analysis of this guidance law is available for targets with active maneuverability, a priori knowledge of the target maneuvering model which is related to the relative distance is needed.The restrictions on target maneuvering model inevitably lead to deviations during realistic maneuvers.

The main works of this paper are presented as follows:Inspired by Refs.28,29, the capturability analysis of the RAPN for arbitrarily high-speed maneuvering targets is conducted.Different with the definition for the capture region in Refs.28,29, this paper defines the capture region in the initial heading angle space based on Ref.6,because capture region in that space is important for the mid-end guidance handover and the analysis is conducted in that space.The analysis of this paper is mainly focused on the parameters and variables in the guidance process, such as target velocity, navigation gain,relative distance, and acceleration deviation.Based on the works proposed by Prasanna and Ghose6who analyzed the capturability of RPN against non-maneuvering target, this paper studies the capturability for arbitrarily high-speed maneuvering targets.The conclusions of this paper are more general than those of Ref.6.

The organization of the remainder of this paper is given as follows.Section 2 presents the intended research problem and the zero effort interception condition.Section 3 gives the capture region for an arbitrarily high-speed maneuvering targets for both the APN and the RAPN.Section 4 performs the numerical simulations to analyze the capturability using APPN and RAPN for an arbitrarily maneuvering target.Section 5 draws some interesting conclusions for intercepting arbitrarily high-speed maneuvering targets.

2.Problem formulation

The initial condition of terminal guidance reached between the high-speed maneuvering targets and the interceptor after the mid-end guidance process can determine the interceptor’s guidance performance against the target.In many existing studies, the initial value of the heading angle is thought to be directly related to the successful interception of the high-speed maneuvering targets.Because this paper focuses on the interception guidance scenario, the high-speed maneuvering target is the intercepted target in this paper.

2.1.Planar pursuit preliminaries

Consider a planar pursuit scenario between an arbitrarily maneuvering target T and an APPN-guided interceptor M,as shown in Fig.1.The assumptions are first introduced into a planar engagement scenario for the interceptor and target.

Assumption 1.The interceptor and target have constant speeds of VMand VT(with a non-dimensional velocity ratio ρ=VT/VM≫1), respectively.

Assumption 2.The effect of the command delay from the overload acceleration to the actual control variable is neglected.

Assumption 3.The maximum detection range of the interceptor seeker is Rmax.If the relative range between the interceptor and target is less than the maximum detection range Rmax, the target is considered to be successfully detected and captured in the interceptor’s field of view.

The engagement scenario shown in Fig.1 is established in the coordinate system XI-OI-YI,where the normal acceleration, LOS, range-to-go, and flight-path angle are denoted as a,q,R,and θ,respectively.The target and interceptor heading angles are denoted as η=θT-qMTand γ=qMT-θM,respectively.

The nonlinear dynamics of the relative motion between the interceptor and target can be formulated as follows:where ˙qMTis the LOS rate between the interceptor and target;and ˙R is the closing velocity, ˙R>0 means that the relative range increases, and ˙R<0 means that the relative range decreases in the guidance process.In this paper’s interception guidance scenario, ˙R<0 is maintained over the entire guidance process.

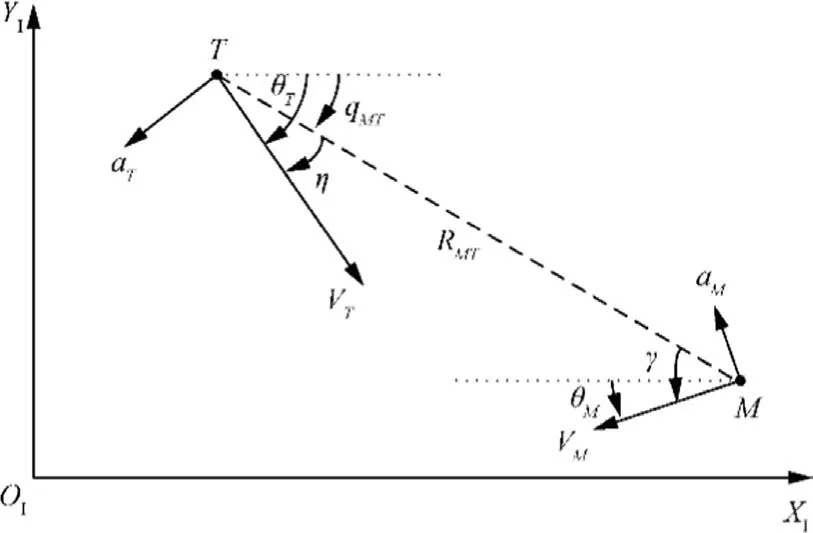
Fig.1 Planar engagement geometry.

The PN guidance law is widely used in the engagement problem because of its simple expression,where the command acceleration is directly proportional to the LOS rate and can be written as aM=N′VMT˙qMT,where N′is the navigation coefficient,and VMTis the closing velocity.Many modern guidance laws have been developed based on the PN guidance law.Although the forms of modern guidance laws are complicated,they are essentially equivalent to proportional guidance with correction terms.Taking the APN guidance law as an example,its general form can be expressed aswhich is the augmented version of TPN.However,the expressions for both the TPN and APN guidance laws contain closing velocity terms VMT, which are difficult to obtain in practical situations.

From a practical implementation point of view, the lateral acceleration is applied normal to the interceptor velocity vector under the assumption of a small angle of attack.Therefore,the PPN guidance law is applied by N′VTM=NVM, which is more widely used than TPN.Therefore, augmentation of PPN guidance law would be much more realistic and relevant.The lateral acceleration of the APPN guidance law can be expressed by

where K is the correction coefficient,K=1 makes the terminal LOS rate converge to zero, and K=3 makes the required terminal acceleration converge to zero,which is the optimal guidance law neglecting the inertial link of the flight control system.

The acceleration of the target aTis arbitrary,bounded,and piecewise continuous in time throughout the engagement.Therefore, by integrating both sides of Eq.(5), we can obtain

2.2.Zero effort interception condition

The interception in the case where the angle between the interceptor velocity vector and the target velocity vector is less than π/2 is named as HO interception, and that in the case where the same angle is greater than π/2 is named as HP interception.

As shown in Fig.2, take the end O′of the target velocity vector VTas the center of the circle,and use the modulus value of the interceptor velocity vector VMas the radius to make a circle, which intersects with the LOS at point A and point B.The interceptor velocity vector is.Ifis established, the condition for HO zero effort interception is satisfied.Ifis established, the condition for HP zero effort interception is satisfied.The HO zero effort interception means that the APN guidance law is applied by interceptor with positive navigation constant, that is, N>0.The RAPN guidance law is applied by interceptor in the HP zero effort interception, where the navigation constant is a negative constant, that is, N<0.

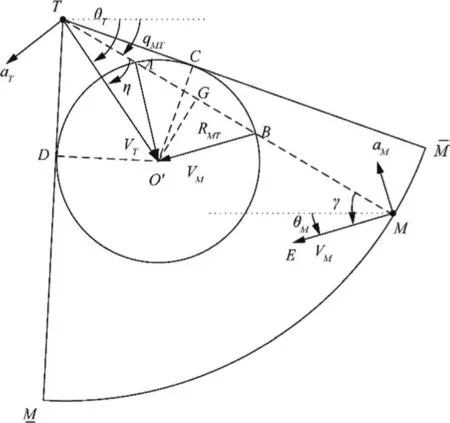
Fig.2 Schematic diagram of zero effort interception.

Lemma 1.For a given value ρ>1, if a point in space （γ，η）reaches the manifold defined by

in finite time, then successful interception is guaranteed.Proof.Substituting Eq.(9) into Eq.(2), we can obtain

It can be further determined from Eq.(9) that

Substituting Eq.(11) into Eq.(1), we find

The result ˙R<0 can be obtained by substituting ρ>1 into Eq.(12), implying that the interceptor and target are close to each other.Based on the result expressed by Eq.(10) that the LOS rate is equal to zero and the result that the interceptor and target are close to each other,a successful interception can be realized.It is noted that another set of cos γ values from Eq.(2)are given by cosfor which ˙qMT=0 but ˙R>0.This completes the proof.

The heading angle of the interceptor can be obtained by Eq.(9) as

With the geometric relationship shown in Fig.2, there are only two values of the interceptor’s lead angle when considering the case γ ∊[-π，π]:

Because γ2=π-sin-1（ρ sin η） for ˙R>0, the result γ=sin-1（ρ sin η） is what this paper intends to analyze.

The zero effort interception condition boundary is obtained when the LOS is tangent to the interceptor’s velocity vector circle.At this time, the heading angle of the interceptor is γ=±π/2.Thus, we can find the heading angle range for the target:

where ηmax=arcsin（1/ρ）.Eq.(15) can also be written as

It can be determined from Eq.(16) that the target heading angle range is closely related to the velocity ratio of the target and interceptor.As the target-to-interceptor velocity ratio increases, the range of heading angles allowed by the target gradually decreases.

Lemma 2.The trajectory guided by the APN or the RAPN guidance law in the space（γ，η）can be represented by a straight line for all values of ρ>1, expressed as

Proof.Substituting ˙θTfrom Eq.(5) after taking the time derivative of Eq.(4), we have

Taking the time derivative of Eq.(6) and substituting Eqs.(3) and (7) into it, we can find that

Substituting Eq.(18) into Eq.(19) yields

Integrating both sides of Eq.(19) yields

where γ0and η0are the initial heading angles of the interceptor and target, respectively.

Then,

The point （γ0，η0+η′） can be defined as the equivalent initial heading angle in the （γ，η） space.If the target implements no maneuvers in the terminal guidance, then η′=0 and the equivalent initial heading angle is equal to the initial heading angle （γ0，η0）.

3.Capture region for an arbitrarily high-speed maneuvering target

This section presents the capture region analysis for an arbitrarily high-speed maneuvering target in the initial heading angle space （γ0，η0）.The complete capture region results against the maneuvering target for both the APN and the RAPN are given.Compared to the capture region for a nonmaneuvering target,the capture region for a maneuvering target is additionally affected by the initial relative distance.The analyzed capture region results provide a heading angle reference for successfully intercepting maneuvering targets.

3.1.Capture region for HO interception

Lemma 3.Assume that the equivalent initial heading angle（γ0，η0+η′）is used as the initial value of the heading angle for the terminal guidance.For ρ>1 and N>0 (HO interception with APN guidance law), the region

defines the capture region of equivalent initial heading angle in （γ，η） space, where

where

and

and then,

Remark 1.Although Lemma 3 gives the capture region for the interceptor in （γ，η） space, the capture region only defines the equivalent initial heading angle.The effects generated by the average turn rate of the target ^anTand the homing phase time t in η′of Eq.(17) can be neglected in （γ，η） space, where the nonlinearity from the initial heading angles γ0and η0to the manifold f（γ，η）=0 is not reflected.The transformation from the equivalent interceptor and target initial heading angles γ0and η0+η′to the manifold f（γ，η）=0 obeys a linear law where the trajectory in （γ，η） space is a straight line with slopeThus, the capture region defined in （γ0，η0） space needs to be given for the initial heading angle.

It is noted that the effects generated by the average turn rate of the target ^anTand the homing phase time t in η′of Eq.(17) cannot be neglected when obtaining the capture region of the initial heading angle.The capture region for the equivalent initial heading angle in （γ，η） space can be refined into an initial heading angle in（γ0，η0）space by considering the effects of the nonlinear terms η′.

Theorem 1.For ρ>1 and N>0 (HO interception with APN guidance law), the region

defines the capture region of the initial heading angle in（γ0，η0） space, where

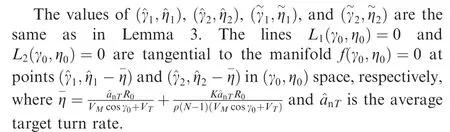
Proof.The target can only be captured by the interceptor when the equivalent initial heading angle γ0, η0+η′of the interceptor and the target lie in the capture region RAPNof the （γ，η） space from Lemma 3.Firstly, the situation that the point of the equivalent initial heading angle （γ0，η0+η′） lying in the capture region A1∩B1is analyzed.The following inequality reflects the relationship between the point and the lines L1（γ，η）=0,and that between the point and the manifold f（γ，η）=0 can be given as

Next,the situation that the point（γ0，η0+η′）lies in the capture region A2∩B2is also analyzed.The following inequality reflects the relationship between the point and the lines L2（γ，η）=0, and that between the point and the manifold f（γ，η）=0 can also be given as

The extreme value of the heading angle appears at the terminal guidance end time, which can be estimated by

where R0and V0are the initial values of the relative distance and the closing velocity, respectively.

From the constraint ｜η｜≤arcsin（1/ρ）given by Eq.(16),the target heading angle value is regarded as small enough with the velocity ratio ρ ≫1.Thus, cos η0≈η0, and the equation can be written as

Substituting Eq.(48) into Eqs.(43)–(46), we have

Therefore, the capture region in （γ0，η0） space is

This completes the proof.

Fig.3 gives the capture region for HO interception given byin （γ0，η0） space.Compared with the capture region presented by Prasanna and Ghose in Ref.6, the boundaries L1（γ0，η0）=0 and L2（γ0，η0）=0 shown in Fig.3 behave as a nonlinear form,the reasons for which is that the boundary suffers from the nonlinear term.It can be seen from Fig.3 that the capture region values on the y-axis are all negative, meaning that the interceptor cannot intercept the target when the target heading angle η0is positive because the capture region suffers from target turning effects.

This section is focused on the HO interception condition,where the APN guidance law with N>0 is used to intercept an arbitrarily maneuvering target.As discussed earlier, HP interception is another condition for intercepting the target and is generated by the RAPN guidance law with N<0.The following section discusses the capture region analysis for the RAPN guidance law.

3.2.Capture region for HP interception

Lemma 4.Assume that the equivalent initial heading angles（γ0，η0+η′） are used as the initial heading angles for the terminal guidance.For ρ>1 and N<0 (HP interception with RAPN guidance law), the region

defines the capture region of equivalent initial heading angle in （γ，η） space, where

where

and

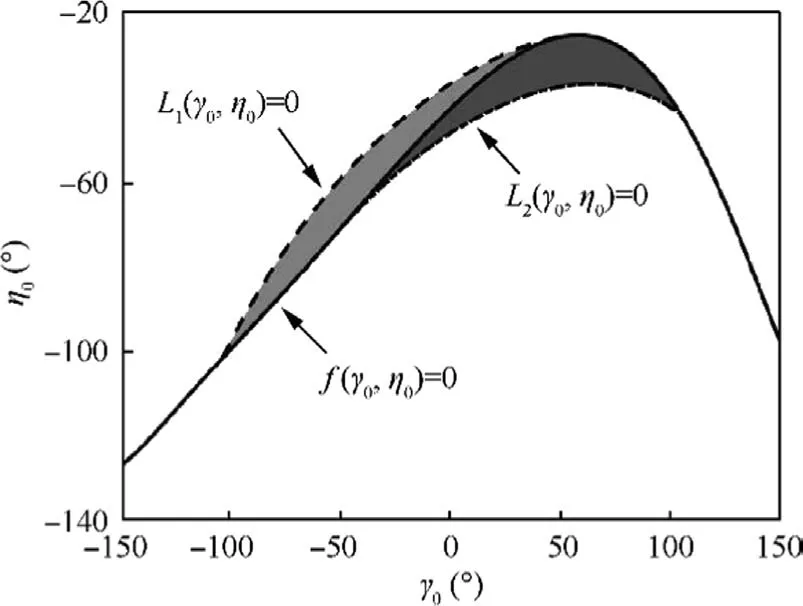
Fig.3 Capture region for HO interception given by .

Proof.There exist the same arguments as given by the proof of Lemma 3, and more details can be obtained from it.

Theorem 2.For ρ>1 and N<0(HP interception with RAPN guidance law), the region of

defines the capture region of the initial heading angle in（γ0，η0） space, where

where

3.3.Acceleration deviation impact on capture region

The concept of the average turn rate ^anT（t）= ^aT/VTis introduced in Section 1.1,1.2,2.1 and 2.2.It is important for calculating the capture region where the zero effort interception manifold f（γ0，η0） and the boundary of the capture region L1（γ0，η0）, L2（γ0，η0）, L3（γ0，η0）, and L4（γ0，η0） mainly depend on the average turn rate ^anT（t）= ^aT/VT.Because of the constant velocity of the target,the average turn rate^anT（t）is determined by ^aT, the average lateral acceleration of the target in terminal guidance, denoted asin Section 2.1.Therefore, the average lateral acceleration value is essential in determining the capture region in （γ0，η0） space.

Remark 2.Although it is said that target maneuvering model is known as a prior knowledge,there still exist great limitations in actual capturability analysis in Ref.28.In target maneuver model assumption of Ref.28, the target maneuvers using an acceleration aTwhich is applied normal to the LOS, and is given by

where b is a nonnegative constant gain and ρ is the relative distance between target and missile.

Eq.(74) gives the prior knowledge of target maneuvering model mentioned in Ref.28, which indicates that acceleration aTis related to the relative distance.Ref.28 intends to simplify the dynamic equations in modified polar variables for capturability analysis by associating acceleration aTwith the reciprocal of the relative distance 1/ρ.Although the dynamic equations have been simplified by the assumption expressed by Eq.(74), it still brings great limitations in actual situation.Thus,capturability analysis presented by this paper is based on the prior knowledge that average accelerationis known in advance.

Remark 3.Because the average lateral acceleration is used in the capture region analysis,Theorems 1 and 2 presented in this paper can be applied to arbitrarily maneuvering targets given prior knowledge about the target’s maneuver.Therefore,this is the point of departure of the analysis presented in this paper from that in Ref.6,29.Apart from measuring the relative motion information at every instant, the implementation of this theorem requires only the a priori knowledge of the target’s maneuvering capability instead of estimating the target lateral acceleration at every instant.Thus, prior knowledge of the average lateral acceleration makes it possible to analyze the capturability so that the heading angle lies in the suitable region to intercept the target successfully.

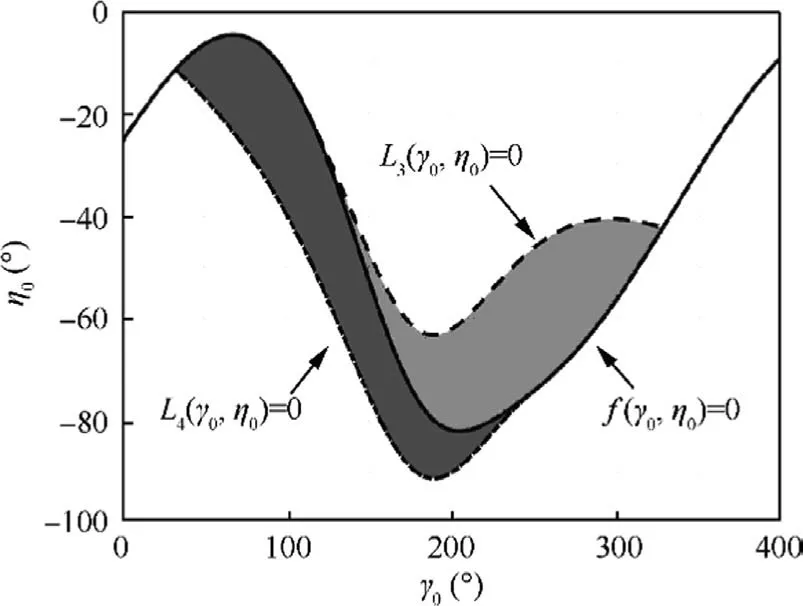
Fig.4 Capture region for HP interception given by .

The above discussion gives the results that the average lateral acceleration of the target is directly related to the accurate solution of capture region and it can be achieved by a priori knowledge about target maneuver.Based on the results, the accurate capture region in the （γ0，η0） space can be given by Theorems 1 and 2 in theory.However, there exists a controversy that the prior knowledge about the target depends on the properties of the target itself which is often not reachable by interceptors, making it difficult to guarantee the accuracy of the average lateral acceleration.The deviation σ is inevitably caused since the average lateral acceleration in the realistic engagement is not equal to that given by priori knowledge.There exists a certain deviation between the capture region calculated by average lateral acceleration in the presence of a priori knowledge and that in realistic engagement, which is caused by the deviation σ.

Fig.5 gives the different capture regions for HO interception with ^aT=40 m/s2, ^aT=30 m/s2, and ^aT=25 m/s2, where^aT=30 m/s2is the true average lateral acceleration, ^aT=40 m/s2is the value from prior knowledge with deviation σ=10 m/s2compared to the true situation, and ^aT=25 m/s2is the value given from prior knowledge with deviation σ=-5 m/s2compared to the true situation.It can be seen from Fig.5 that the intersection is generated between the realistic capture region and the capture region with deviation σ=10 m/s2,which means that the capture region in intersection still enables the zero effort interception to be satisfied when the average lateral acceleration given by prior knowledge has the deviation σ=-5 m/s2with the realistic value.This indicates that the deviation σ=-5 m/s2is a suitable value given by the prior knowledge within an acceptable margin of deviations.But there is not intersection between the realistic capture region and the capture region with deviation σ=10 m/s2,which means that no intersection is generated by two capture regions to ensure the zero effort interception to be satisfied when the average lateral acceleration given by prior knowledge has the deviation σ=10 m/s2with the realistic value.This indicates that the deviation σ=10 m/s2exceeds the acceptable margin of deviations so that the zero effort interception cannot be guaranteed whatever initial heading angles are.

The above discussion shows that an acceleration deviation from mismatched prior knowledge impacts capturability.Therefore,we analyze the impact of the acceleration deviation on the capture region as follows.

Theorem 3.For ρ>1 and N>0 (HO interception with APN guidance law), the region

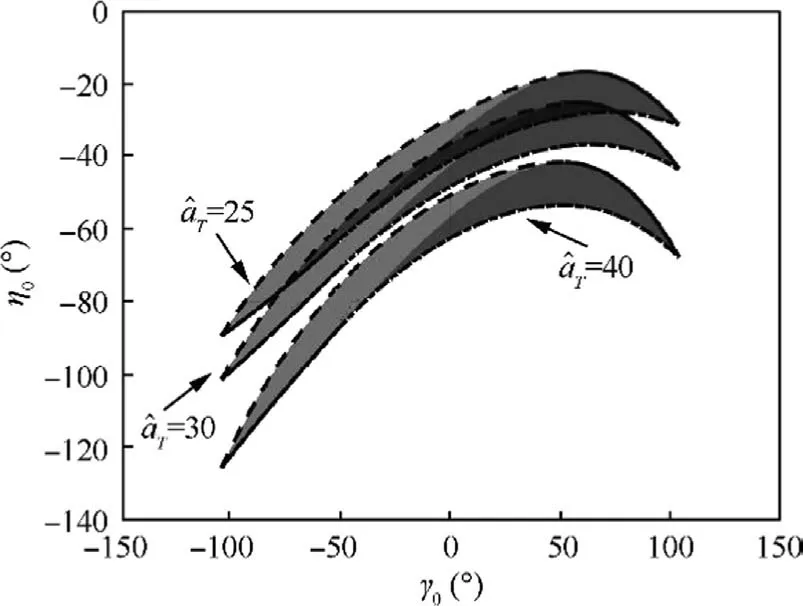
Fig.5 Different capture regions for HO interception with^aT =40 m/s2(acceleration deviation σ=10 m/s2),^aT =30 m/s2(true value),and ^aT =25 m/s2(acceleration deviation σ=-5 m/s2).

defines the sets of acceptable average lateral acceleration deviations σ to intercept the target successfully for an initial interceptor heading angle γ0, where

where

Case 1.For σ>0, the capture region calculated using+σ gradually moves down as the deviation increases in （γ0，η0）space from Fig.5.When the deviation σ belongs to an acceptable deviation margin, an intersection between the true capture region and the capture region with deviation σ is guaranteed.

The boundary of the capture region with acceleration deviation σ can be represented as

It can be seen from Fig.5 that the intersection between the boundaryof the capture region with deviation and the boundary L2（γ0，η0） of the true capture region can be found.Thus, the inequality-L2（γ0，η0）>0 can be satisfied, yielding

Then,the lower boundary of the acceleration deviation can be obtained:

Case 2.For σ<0, the capture region calculated using ^aT+σ gradually moves up as the deviation decreases in（γ0，η0）space from Fig.5.When the deviation σ belongs to an acceptable deviation margin, an intersection between the true capture region and the capture region with acceleration deviation σ is guaranteed.

It can be seen from Fig.5 that the intersection between the boundary L1（γ0，η0） of the capture region with deviation and the boundary Lσ2（γ0，η0） of the true capture region can be found.Thus, the inequality Lσ2（γ0，η0）-L1（γ0，η0）<0 can be satisfied, yielding

Then,the upper boundary of the acceleration deviation can be obtained:

The lower boundary D1（γ0，σ）=0 and the upper boundary D2（γ0，σ）=0 of the acceleration deviation σ have now been obtained, completing the proof.

Theorem 4.For ρ>1 and N<0(HP interception with RAPN guidance law), the region

defines the sets of acceptable average lateral acceleration deviations σ to intercept the target successfully for initial interceptor heading angle γ0, where

where

Table 1 Initial parameters for interception engagement simulation.

Fig.6 Capture intervals for HO (top image) and HP (bottom image)interception with η0 =-60° for different navigation gains.

Proof.The arguments used to prove Theorem 3 can also be used to prove Theorem 4.Please see the proof of Theorem 3 for details.

Fig.7 Capture interval lengths of γ0 for HO(top image)and HP(bottom image) interception with different values of η0.

4.Simulation analyses

This section performs numerical simulations to analyze the capturability using APN and RAPN for an arbitrarily maneuvering target.First, the initial conditions are given for the terminal guidance between the interceptor and the target.Subsequently, capturability analyses for the maneuvering target for HO interception with APN and HP interception with RAPN are implemented.The results are used to show that increasing the target’s velocity can weaken the capturability and that the acceleration and relative distance can change the capture interval’s direction in polar coordinates but not its length.Finally, the acceleration deviation analysis for the average acceleration is implemented,with the significant result that HP interception has a better deviation fault tolerance compared with HO interception and the deviation’s fault tolerance can weaken as the relative distance increases.

4.1.Capturability analysis for maneuvering target

The initial conditions for the capturability simulation of the interceptor using HO and HP interception are set in Table 1.The velocity ratio ρ=VT/VM=2>1 can be obtained from Table 1, and the models used are simple kinematic models,as given in Section 2.1.

Fig.6 presents the possible capture interval of both the HO interception and HP interception with η0=-60°for different values of N.The capture interval corresponding to the initial flight directions of the interceptor is defined in polar coordinates.It can be seen from Fig.6 that the HP interception capture interval is larger than the HO interception capture interval at the same absolute value of N.The capture interval shrinks as the absolute value of N decreases.

Fig.7 shows the capture interval length of γ0for different values of η0for HO and HP interception.As soon as the target enters the terminal guidance so that the initial parameters are determined, the capture region of the interceptor can be ensured for the different initial target heading angles η0.It can be observed from Fig.7 that the target is capturable by the interceptor only for η0in the interval [-101.22°，-25.24°]for HO interception and only in the interval[-91.29°，-4.55°] for HP interception.Successful interception cannot be realized when the initial value η0is outside these intervals.The maximum value of the capture interval length occurs at η0=-36.75°for HO interception and η0=-63.24°for HP interception.The maximum value of capture interval length for HP interception is larger than that for HO interception, indicating that HP interception, where RAPN is used to intercept the target,has a larger interception range than HO interception.

Fig.8 shows the possible capture intervals for both HO and HP interception with η0=-60°at different target velocities.The capture interval shrinks as the target velocity increases because the velocity ratio ρ=VT/VMincreases with increasing target velocity.This result verifies that the high-speed maneuvering targets are more difficult to capture than low-velocity targets, and the capturability of high-speed targets decreases as the target velocity increases.Thus, increasing the target velocity, which increases the velocity ratio ρ, weakens the interceptor’s capturing ability.

As shown in Fig.5, the capture region in （γ0，η0） space moves in the negative direction of the y-axis as the average target acceleration increases.The target cannot be intercepted for positive values of η0because the calculated capture region is completely on the negative part of the y-axis.Because the average acceleration’s impact on the capture region is reflected mainly on the y-axis, a suitable γ0is selected to facilitate the analysis of the acceleration effect on the capture region.Fig.9 presents the possible capture intervals for HO interception with γ0=50°and HP interception with γ0=200°for different average accelerations.It can be seen from Fig.9 that the acceleration can only change the capture interval’s location in polar coordinates but not its length.

Similarly,the impact of the relative distance on the capture region is mainly reflected on the y-axis.Fig.10 presents the possible capture intervals for HO interception with γ0=50°and HP interception with γ0=200°for different relative distances.These results also indicate that the relative distance can only change the capture interval’s location in polar coordinates but not its length.The important conclusion is that the average target acceleration and the initial relative distance only affect the capture region’s location but not its size in （γ0，η0）space.

Fig.11 shows the capture region for HO interception guided by PN and HP interception guided by RPN against non-maneuvering target, which is a special case of this paper proposed by Prasanna and Ghose6where the target’s acceleration is equal to zero.Fig.12 shows the capture region for HO interception guided by PN and HP interception guided by RPN against maneuvering target, which is another special case where the correction coefficient K of command acceleration shown by Eq.(7) is equal to zero.Because the above two cases are two special cases of this paper where one case is that the acceleration of target is equal to zero and another case is that the correction coefficient K of command acceleration is equal to zero, the conclusion given by the analysis in this paper can be applied to both two cases as well.

4.2.Acceleration deviation analysis

Figs.13 and 14 are effective capture region for HO and HP interception with inaccurate target maneuver caused by the mismatched acceleration deviation σ respectively.As can be seen from Figs.13 and 14, the capture region marked by dark shades is the realistic one which is provided by the real target maneuver=15 m/s2,and the captureregionmarked by light shadesis the inaccurate one which is provided by the inaccurate target maneuver+σ generated by mismatched prior knowledge.In Figs.13 and 14, the values of deviation σ are taken as ｜σ｜=5，10，14 m/s2so that the variation of effective capture region can be displayed.The effective capture region,the intersection of the dark shades and the light shades in Figs.13 and 14,is the region that the successful interception can still be achieved while the inaccurate target maneuver=+σ generated by mismatched prior knowledge cannot be avoided.It is manifested that the initial heading angle of interceptor and target γ0,η0lying in the effective capture region can guarantee the successful interception.The effective capture region shrinks as the absolute value of acceleration deviation ｜σ｜increases for HO and HP interception from Figs.13 and 14, that is, successful interception will become increasingly difficult to achieve.Fig.15 shows the capture interval lengths of η0for HO (top image) interception at γ0=35°and HP(bottom image)interception at γ0=220°with different values of σ.Compared with HO interception, HP interception can produce a larger effective capture region under the same deviation condition from Figs.13-15, which manifests that the HP interception has a better deviation fault tolerance.

Fig.12 Capture region for HO interception guided by PN (left image) and HP interception guided by RPN (right image) against maneuvering target.

Fig.13 Effective capture region for HO interception with inaccurate target maneuver caused by mismatched acceleration deviation σ.

Fig.16 presents the acceptable acceleration deviations for HO and HP interception.The acceptable acceleration deviation formulation is presented in Section 3.3,which means that the acceleration deviation caused by the mismatch between the acceleration values in presence of the prior knowledge and the realistic values causes the deviation of the capture region.If the deviation is within a reasonable range, as shown in the shaded areas of Fig.16, the capture region in intersection between the capture region obtained by prior knowledge and that obtained by realistic value still enables the zero effort interception to be satisfied.If the deviation is not within a reasonable range, the intersection cannot guarantee that a zero effort interception occurs.It can be seen from Fig.16 that the acceptable deviation region for HP interception is larger than that for HO interception and the region is not affected by the values of average acceleration.

Fig.17 shows the acceptable acceleration deviation ranges for HO and HP interception with different navigation gains.The acceptable acceleration deviation range increases as the absolute value of N increases, and the navigation gains have a greater impact on the HO interception acceptable acceleration deviation range than on HP interception.Larger absolute values of N values make the deviation fault tolerance higher.

Fig.16 Acceptable acceleration deviation ranges for HO (top image) and HP (bottom image) interception.

Fig.17 Acceptable acceleration deviation ranges for HO (top image) and HP (bottom image) interception with different navigation gains.

Fig.18 shows the acceptable acceleration deviation ranges for HO and HP interception at different target velocities.Notably, the acceptable acceleration deviation range shrinks as the target velocity increases for HO interception, but the opposite trend occurs for HP interception.Fig.19 shows the acceptable acceleration deviation ranges for HO and HP interception with different relative distances.The acceptable acceleration deviation range shrinks as the relative distance between the interceptor and target increases, indicating that larger relative distances weaken the fault tolerance.

The above analysis of the guidance parameters for deviations provides a reference for target interception.Suitable initial conditions for the terminal guidance can improve the probability of successful interception.

5.Conclusions

Capturability analysis of APPN and RAPN for arbitrarily high-speed maneuvering targets are conducted in this paper.The analysis is available for any target with arbitrarily maneuvering form since the concept of average acceleration is introduced, which can be known by a prior knowledge about the target maneuver.Different from the previous studies, the acceleration deviation analyses are implemented, where the deviation stems from the mismatch between the prior knowledge and the realistic maneuver.The studies proposed by Prasanna and Ghose6can be seen as a special case of this paper when the acceleration of the target is equal to 0 m/s2.

Fig.18 Acceptable acceleration deviation ranges for HO (top image) and HP (bottom image) interception at different target velocities.

Some interesting conclusions can be drawn via numerical simulation.The capturability of interceptor for the highspeed targets decreases as the velocity of that target increases,which verifies that the high-speed targets are more difficult to capture than low-velocity targets.The average acceleration and the initial relative distance only have the effect on the location of the capture region but not the size of it in the （γ0，η0）space.In the analysis of the acceleration deviation, the results manifest that the larger relative distance of the target can weaken the fault tolerance more for the deviation and the velocity has true opposite effect on the HO interception and the HP interception.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No.62073335), the Science Fund for Distinguished Young People in Shaanxi Province, China(No.2022JC-42),and the China Postdoctoral Science Foundation (Nos.2017M613201, 2019T120944 and 2020M683737).

Fig.19 Acceptable acceleration deviation ranges for HO (top image)and HP(bottom image)interception with different relative distances.