引水隧洞涌水量最优预测方法研究
王成华,牛来福
(山东润泰水利工程有限公司,山东 泰安 271000)
0 引言
引水隧道广泛应用于各种水利工程中,包括供水工程、灌溉工程、水电站工程、城市排水工程等。通过引水隧道,可以将水源从水源地输送到用水区域,满足城市和农田的用水需求,实现水资源的合理利用。随着国家“十三五”计划的进行,促进了我国大量的道路交通、矿山、水利、城建等工程建设,隧道的建设不论是在建设规模还是建造数量都取得了很大的进步[1]。但是在施工过程中也遇到了一些工程问题,其中隧道的突涌水的发生给建设施工带来了不小的挑战。
目前很多学者针对隧道突涌水预测取得了很多成果,马国民[2]针对岩溶隧道发生突涌水断面进行研究,建立概化计算模型,对突涌水过程进行数值模拟,得到了隧道围岩的变形演化规律。资西阳等[3]对断层破碎带突涌水影响因素采用AHP熵权法得到指标权重,进而确定灾害发生概率等级,根据灾害发生概率等级和灾害后果等级确定隧道突涌水灾害风险等级。刘常昊等[4]提出一种基于地质雷达的隧道涌水量预测方法,对隧道圆形空洞结构运用MATLAB进行地质雷达正演模拟,建立了结构模型,提供了一种科学的涌水量预测方法。
虽然在隧道涌水量预测方面取得了很多的研究成果,但关于引水隧洞涌水量的研究还比较少,本文通过对部分隧道突涌水问题进行总结分析,得到其内在规律,然后基于偏最小二乘法的多元线性回归方程和LSTM对引水隧洞涌水量进行预测,通过与实际结果进行对比,比较2种预测方法的准确性,为实际工程应用提供参考。
1 工程案例统计与分析
本文通过对隧道施工过程中的突涌水事故案例进行统计分析,由于篇幅原因仅展示部分案例见表1,对案例进行综合分析得到突涌水的内在规律。

表1 工程案例统计表
1.1 突涌水事故埋深和长度分布特征
根据GB 50487—2008《水利水电工程地质勘察规范》[5]可知,以埋深600m为分界,深埋的埋深超过600m,浅埋的埋深小于600m。按照规范,对上述20个工程案列进行统计分析,得出隧道(洞)的埋深和长度所占比例,如图1—2所示。

图1 埋深统计

图2 长度统计
由图1—2可知,上述事故案例中,64%为浅埋,并且长隧道所占比例较大,达到了74%,所以可以得出突涌水事故更容易发生在浅埋的长隧道工程中。
1.2 突涌水事故不良地质、出水位置和涌水量分布特征
根据已有的研究成果将突涌水事故分为隧道岩溶类、地下暗河、岩层裂隙和隧道断层类4大类[6],如图3所示展示了突涌水事故隧洞不良地质统计。上述案例出水位置和涌水量统计图如图4—5所示。

图3 突涌水事故隧洞不良地质统计

图4 突涌水事故出水位置统计
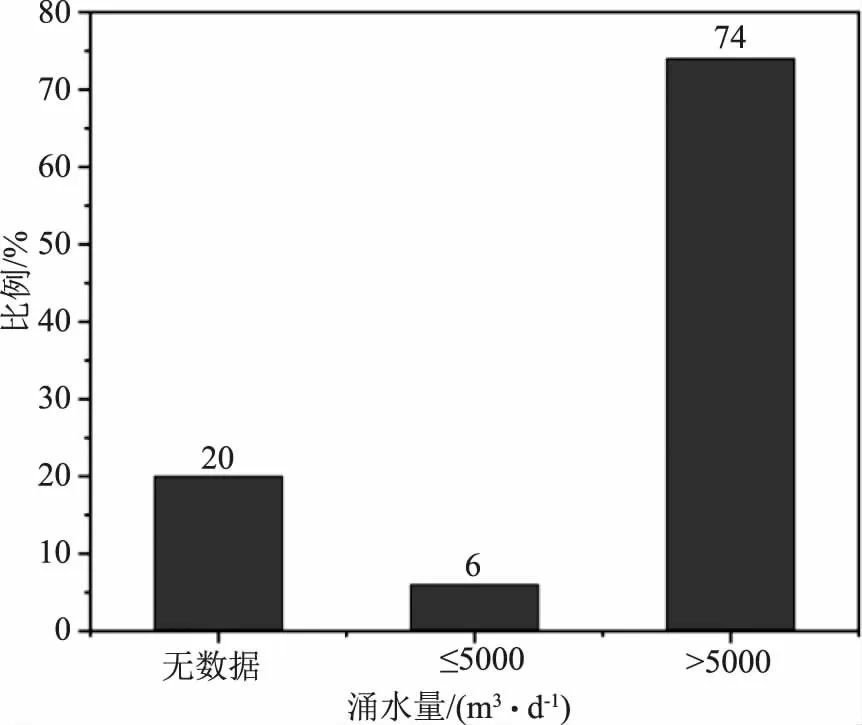
图5 涌水量统计
由图3可知,在隧道突涌水事故中由断层与岩溶类导致的事故所占得比例最大,达到了78%,这说明在断层与岩溶类的地质中要做好突涌水事故的防护。由图4—5可知,掌子面出水所占的比例最大,达到了50%,最大涌水量为5000m3/d以上达到了74%。
2 预测方法比较
LSTM是一种专门用于处理序列数据的深度学习模型,广泛应用于自然语言处理、语音识别、时间序列预测等领域。偏最小二乘回归是一种常用于处理多变量数据的统计建模方法,主要目的是通过对多个自变量和因变量之间的线性关系进行建模,进行预测和探索数据的内在结构。在本研究中采用LSTM和基于偏最小二乘法的多元线性回归方程,对涌水量进行预测,通过试验结果与工程案例对比选出最优的预测方法。
2.1 预测方法
2.1.1LSTM法
LSTM具有更强的记忆能力,能够处理长时依赖关系,并且对于梯度消失和梯度爆炸等问题有较好的解决能力。LSTM的计算过程可以分为以下几个主要步骤:
(1)输入门:通过对输入数据和先前的隐藏状态进行逐元素乘法和sigmoid激活函数操作,生成一个介于0~1之间的值,表示要保留的信息的权重。
(2)遗忘门:通过对输入数据和先前的隐藏状态进行逐元素乘法和sigmoid激活函数操作,生成一个介于0~1之间的值,表示要遗忘的信息的权重。
(3)记忆状态更新:通过将输入数据和先前的隐藏状态进行逐元素乘法和双曲正切激活函数操作,生成一个新的记忆状态。这一步骤主要通过输入门和遗忘门来控制,从而决定记忆状态中哪些信息应该被更新。
(4)输出门:通过对输入数据和当前的记忆状态进行逐元素乘法和sigmoid激活函数操作,生成一个介于0~1之间的值,表示要输出的信息的权重。然后,通过将记忆状态进行双曲正切激活函数操作,将其映射到-1~1之间的范围内,作为LSTM单元的输出。
(5)隐藏状态更新:通过将输出门和当前的记忆状态进行逐元素乘法操作,生成一个新的隐藏状态。这一隐藏状态将作为下一时刻的输入,参与后续的计算过程。
2.1.2基于偏最小二乘法的多元线性回归
偏最小二乘回归是一种用于建立预测模型的统计方法,它可以处理多重共线性问题,特别适用于在自变量(X)和因变量(Y)之间存在高度相关性的情况。数学原理如下:
假设有n个样本和p个自变量,自变量矩阵为X(大小为n×p),因变量矩阵为Y(大小为n×1)。首先,对自变量矩阵X和因变量矩阵Y进行标准化处理,使得它们的均值为0,方差为1,即:
X′=(X-mean(X))/std(X)
(1)
Y′=(Y-mean(Y))/std(Y)
(2)
式中,mean(X)—X的列均值;std(X)—X的列标准差。
然后,通过对X′和Y′进行偏最小二乘分解,得到2组新的综合变量:X的投影矩阵T(大小为n×k,其中k为综合变量个数),Y的投影矩阵U(大小为n×k),以及X的载荷矩阵P(大小为p×k)和Y的载荷矩阵Q(大小为1×k)。这些矩阵的计算过程可以用以下公式表示:
T=X′×W
(3)
U=Y′×C
(4)
P=X′×W×inv(W′×W)
(5)
Q=Y′×C×inv(C′×C)
(6)
式中,W—X′、Y′之间的权重矩阵(大小为p×k);C—Y′的权重矩阵(大小为1×k);inv—矩阵的逆运算。
接着,通过对T和U进行线性回归,得到X和Y之间的回归系数B(大小为p×1),即:
B=inv(P′×P)×P′×U
(7)
这个回归系数B可以用来建立多元线性回归模型:
Y=X×B
(8)
最后,可以通过交叉验证等方法来评估模型的性能,并选择最优的综合变量个数k,以优化模型的性能。
2.2 建模过程
(2)数据预处理:通常需要对数据进行标准化处理,使其具有零均值和单位方差,以避免因不同变量尺度的差异而对模型产生不良影响。
(3)拟合偏最小二乘模型:通过对自变量和因变量之间的投影误差进行最小化,得到一组新的综合变量(称为偏最小二乘回归分量),并通过对这些分量进行回归分析来建立多元线性回归模型。
(4)模型评估和选择:建立偏最小二乘回归模型后,需要对其进行评估和选择。常见的评估指标包括均方误差、均方根误差、决定系数等,用于评估模型的拟合效果和预测能力。
(5)模型应用:在完成模型评估和选择后,将训练好的偏最小二乘回归模型应用于新的数据进行预测。输入新的自变量特征值,通过模型的预测函数得到对应的因变量目标值。
2.3 样本选取
本次样本由国内外记录的隧洞涌水案例组成,选择埋深H、地下水位h和岩石质量指标RQD作为预测参数。
(1)隧道埋深:较大的埋深可以提供更多的土层或水层作为覆盖层,有助于保护隧道结构免受外界力的作用,减小地表沉降和地面震动的影响。
(2)地下水位:地下水位是隧道突水的一个重要因素,对隧道的稳定性和安全性有着显著的影响。地下水位的高低会对隧道突水的发生概率、涌水量以及涌水速度产生影响。
通过对“金口”连头处精确测量、计算、下料等方面考虑,降低连头施工中各因素的不利影响,并由经验丰富、技术水平高而且责任心强的焊工进行施焊,通过制定科学的“金口”施工人员管理制度和激励机制,并根焊热焊后加密检测等质量控制措施,从而提升长输管道“金口”连头的整体施工效率和质量。
(3)RQD:岩石的裂隙对隧道内涌水有着较大的影响,广泛应用于岩石工程、地质勘探、隧道工程、岩土工程等领域。RQD的取值范围为0%~100%,数值越高,表示岩石质量和完整性越好。
当训练和测试预测模型的数据量足够大时,可更全面地捕捉到数据的分布、趋势和规律,能够建立更为准确和稳健的预测模型。大数据集可以提供更多的样本,让模型更好地学习数据的特征,在实际应用中具有更好的泛化能力[7]。对国内外100例工程案例进行分析,将其中的90组用来训练模型,另外10组用来测试模型的准确性。由于篇幅有限仅列出部分5组测试样本,见表2。
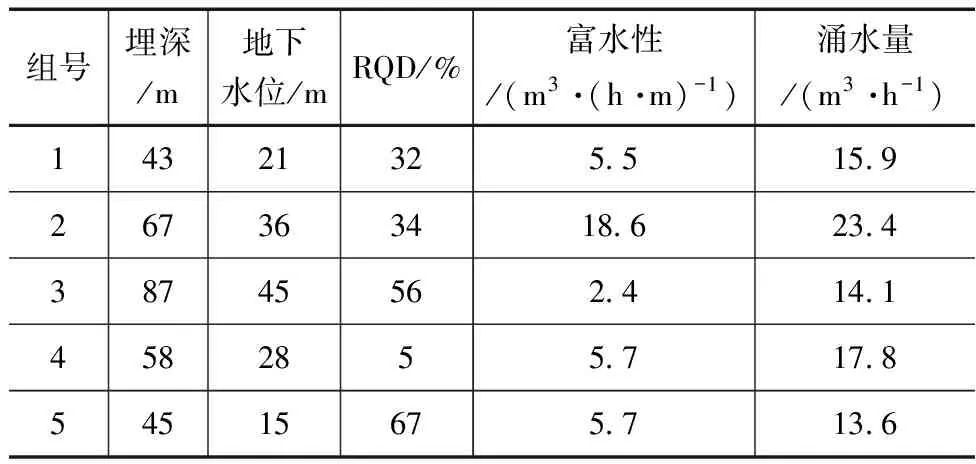
表2 测试样本库
2.4 方法比选
通过上面2种方式预测后,需将预测值与实际值进行比较,判定预测模型的准确性。为了描述预测的准确性,选用以下3个统计指标对预测结果进行评价:
(9)
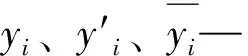
(10)
式中,EMAE—平均绝对误差。
(11)
式中,EMSE—均方误差。
2种不同预测模型的3项统计指标见表3。

表3 预测结果对比表
其中R2反应实际值与模型预测值的一致性,R2越大,预测结果越接近实际值,预测更准确。EMAE和EMSE的数值大小反映预测结果的准确程度,其值越小,准确度越高。通过表3可以看出与基于偏最小二乘法的多元线性回归方程预测对比,LSTM的预测结果中R2较大,且EMAE和EMSE的数值更小,更加准确,所以LSTM的预测准确性更好。
3 结论
本文通过对部分隧道突涌水问题进行总结分析,得到其内在规律,然后基于偏最小二乘法的多元线性回归方程和LSTM对引水隧洞涌水量进行预测,主要得到以下结论。
(1)通过对工程案例进行分析可以得出突涌水事故更容易发生在浅埋的长隧道工程中,并且掌子面出水所占的比例最大。
(2)通过对比发现LSTM的预测结果准确性要高于基于偏最小二乘法的多元线性回归方程,可以在实际工程中为引水隧洞涌水量的预测与防护提供参考。

