一题一课 凸显本质
陈志婷 庞凰琴


[摘 要] 數学复习课普遍存在重点、难点题目堆砌,教师讲得多学生练得多的问题,长此以往,容易造成师生身心疲惫,学习效率不佳等现象. 采用“一题一课”复习方法,渗透一题多变、一题多解、多解归一的数学思想,能更好地凸显问题的本质. 文章主要从“优选引题,揭示问题本源”“注重通法,提升思维深度”“拓展变式,发展数学素养”三方面详细阐述“一题一课”复习方法.
[关键词] 一题一课;策略引导;数学本质
在深化教育改革的今天,数学知识、思想、方法、观念都是在解决问题的过程中发展起来的. 教师应该及时发现学生的学习困惑,尤其是重、难点问题,复习时要有针对性、系统性和启发性[1]. 而善于寻找典例,巧用变式与拓展,能达到对学生思维的训练,能使他们成为思维活跃、勤于观察、善于思考、敢说敢做、勇于创新的人.
教学时教师应在紧扣教材的同时,合理设计一题一课式变式训练,通过训练,让学生更加深刻地理解所学知识,从而促进和增强学生思维的深刻性与延展性,充分培养学生思维的应变能力、想象力及创造力. 只有这样,学生才会更自信,更愿意去交流探索,从而真正地成为学习的主人.
教学微设计
1. 引题呈现
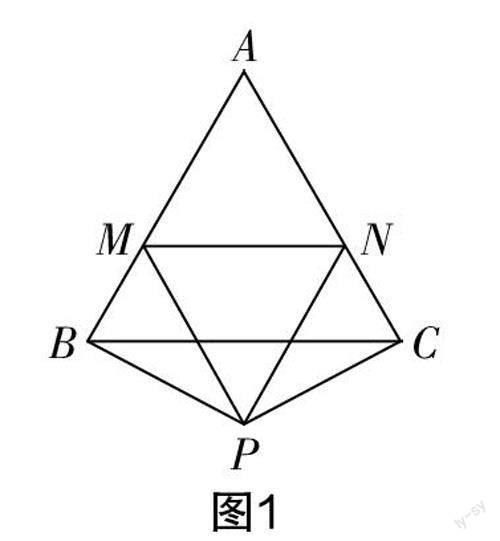
引题 在等边三角形ABC的两边AB,AC所在直线上分别有M,N两点,P为△ABC外一点,且∠MPN=60°,∠BPC=120°,BP=CP. 探究:当M,N两点分别在直线AB,AC上移动时,BM,NC,MN之间有怎样的数量关系.
(1)如图1所示,当M,N两点分别在边AB,AC上,且PM=PN时,试说明MN=BM+CN.
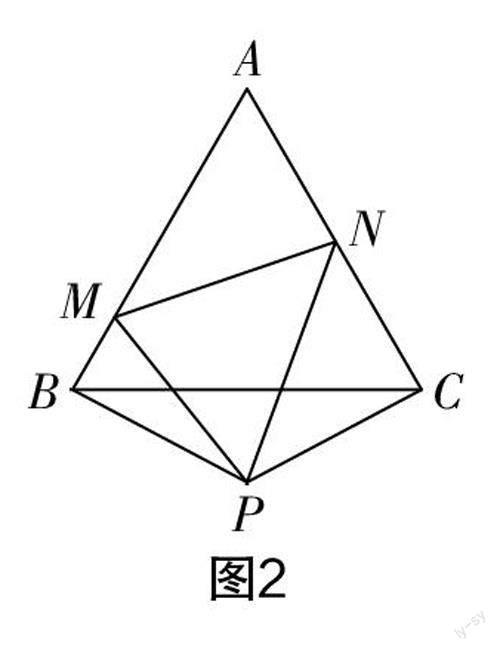
(2)如图2所示,当M,N两点分别在边AB,AC上,且PM≠PN时,MN=BM+CN还成立吗?
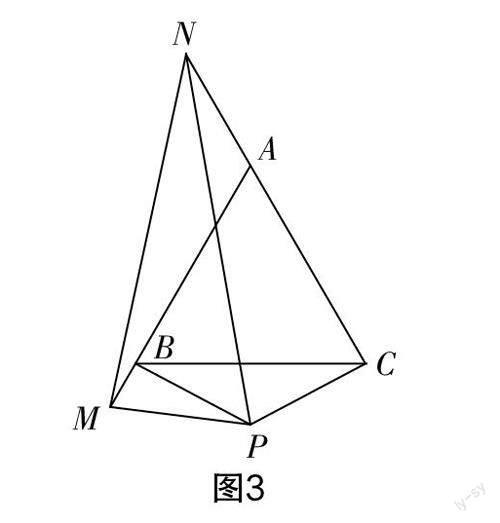
(3)如图3所示,当M,N两点分别在边AB的延长线和CA的延长线上时,请直接写出BM,NC,MN之间的数量关系.
2. 背景分析
本题是七年级下册数学2020学年期末考试的一道压轴题,学生望而却步. 从答题反馈来看,不尽如人意,学生添加的辅助线五花八门,让人眼花缭乱. 由于认知水平不同,理解不同,思路不同,所以学生解决此题时给出了多种解法. 对于此题,很多学生有大致的求解思路,但很模糊,找不到最佳解法,导致解题书写逻辑混乱,费时费力. 为了有效提高学生思维的深度和广度,渗透思想方法,培养学生领悟通性通法,笔者针对这道题进行了“一题一课”微专题设计,并进行变式和拓展,引导学生在解决此题的基础上,学习数学知识,领悟数学思想方法,发现数学问题的本质,提高数学解题能力.
3. 解法探究
下面以第(1)问为例. 从学生的答题情况来看,第(1)问的求解方法琳琅满目,但归纳起来,本质是“截长补短”,具体求解过程如下.
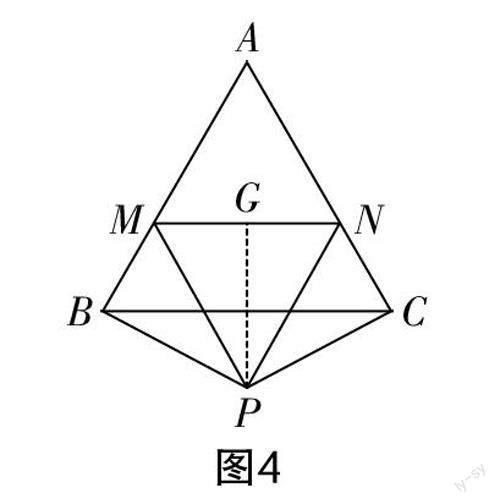
解法1:要说明MN=BM+CN,通常采用的方法是“截长补短”. 因为PM=PN,根据等腰三角形的性质,不难想到如图4所示的辅助线,即取MN的中点G,连接PG(当然也可以过点P作PG⊥MN,垂足为G,或作∠MPN的平分线交MN于点G),先证明△BPM≌△CPN,再证明△BPM≌△GPM,△CPN≌△GPN,得到BM=MG,CN=NG,进而得到MN=BM+CN.
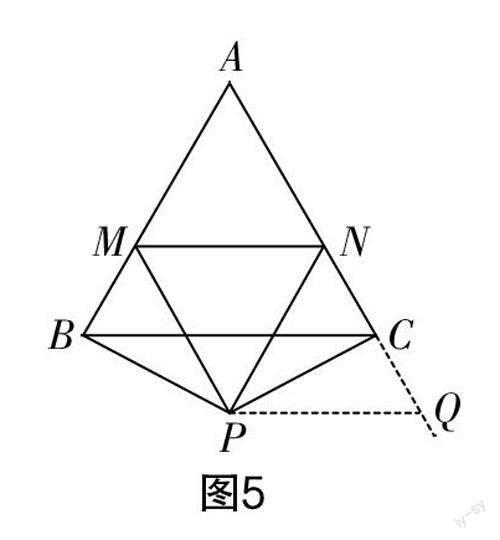
解法2:有学生想到了“补短”的方法,即在NC(或MB)的延长线上截取一条与BM(或CN)等长的线段. 根据这一想法,可作出如图5所示的辅助线,即延长NC至点Q,使CQ=BM,连接PQ. 易证得△MBP≌△QCP(SAS),从而得到∠MPB=∠QPC,PM=PQ. 因为∠MPN=60°,∠BPC=120°,所以∠MPB+∠NPC=60°. 从而得∠NPC+∠QPC=60°,即∠NPQ=60°. 所以∠NPQ=∠NPM. 再证明△MPN≌△QPN(SAS)即可.
对于解法2,有学生想到了可以少证一次全等的优化方法,即把△MPB绕点P顺时针旋转120°后得到△QPC,这样可以直接得到∠MPB=∠QPC,PM=PQ. 笔者大力表扬了该同学,称赞他有独特的见解,获得了简捷的求解方法. 随着课堂的深入,学生的思维活跃了,他们交流讨论着还有没有其他的求解方法. (这表明学生正初步由“学会”向“要学”转变)
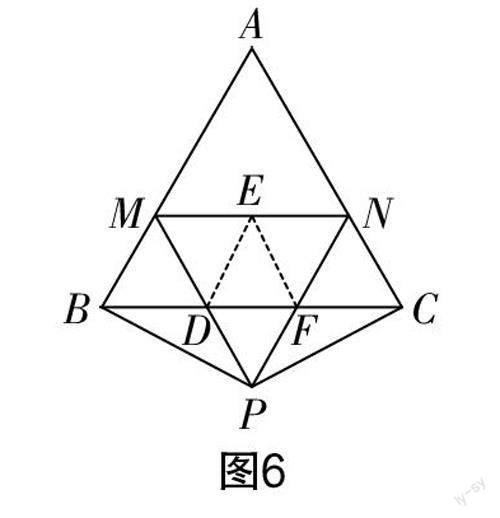
解法3:此时有一名学生说出了采用“截短”方法的另一种作法. 即过点D(点D为PM与BC的交点)作DE∥AB交MN于点E,过点F(点F为PN与BC的交点)作FE′∥AC交MN于点E′(如图6所示). 该学生说利用这种方法只需要说明点E与点E′重合,即只需要证明∠MED+∠DEF+∠FEN=180°.
笔者表扬了提出解法3的学生,赞扬他逻辑性强. 不过也指出,这种解法的步骤会比较冗长.
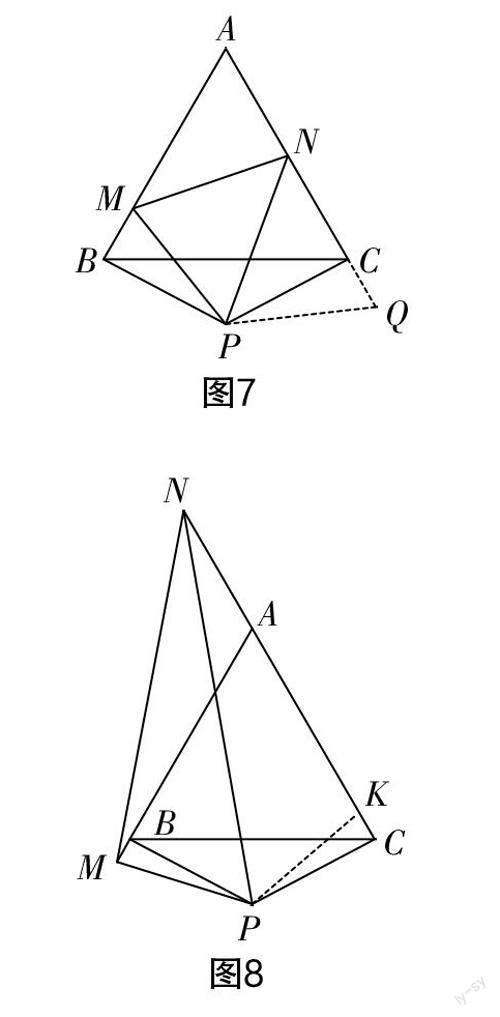
有了第(1)问的求解经验,第(2)(3)问的图形虽然比较复杂,但本质相同,所以“截长补短”这一通法依然适用. 求解第(2)(3)问的辅助线详见图7(补短)和图8(截长).
试题主要考查学生对“截长补短”法的应用,通过作辅助线利用转化思想分析问题和解决问题. 在教学过程中,笔者引导学生抓住问题的本质,对不同的解题策略及多种解法的优劣等进行积极反思,使学生理解知识点的内涵和掌握解决问题的技巧,并让学生从反思中吸取经验教训,达到举一反三、促进思维能力不断提升的效果[2].
4. 迁移应用
问题1 如图9所示,M,N两点分别在正方形 ABCD 的边 BC,CD上,且∠MAN = 45°,连接MN. 求证:MN=BM+DN.
分析 前面在等边三角形的基础上利用“截长补短”法很好地解决了三边数量关系问题,本题是在正方形的基础上探索三边数量关系,本质没有变,只需要把前面的知识迁移过来即可.
解法1 如图10所示,把△ABM沿AM翻折后得到△AEM,易知BM=ME,再通过证明△EAN≌△DAN,得DN=EN,进而有MN=BM+DN.
解法2 如图10所示,将△ABM绕着点A逆时针旋转90°后得到△ADE,证明△MAN≌△EAN,进而得到结论.
变式 在“问题1”的基础上,点A到线段MN的距离是否为定值?
分析 此变式是对“问题1”的直接应用,只要明白(图10中)AE⊥MN,AB=AE,此变式就迎刃而解了.
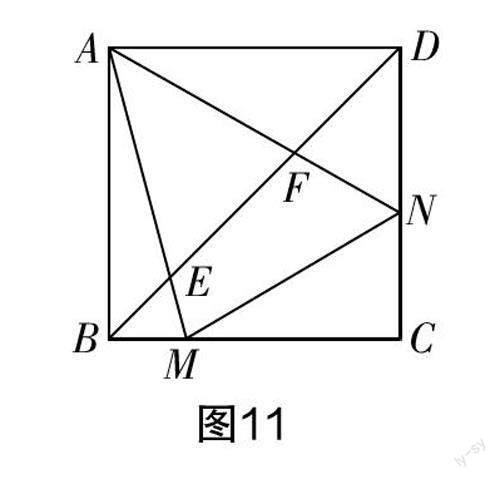
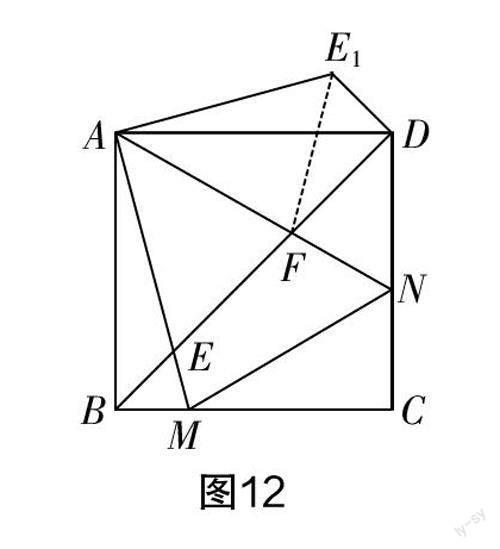
问题2 如图11所示,M,N两点分别在正方形 ABCD 的边 BC,CD上,且∠MAN = 45°,连接MN,BD,BD分别与AM,AN 交于点E和点F,则EF 2=BE 2+DF 2成立吗?
分析 看到结论,联想到勾股定理,于是我们把三条边通过变换放到一个直角三角形中. 如图12所示,把△AEB逆时针旋转90°后得到△AED,连接E1F,易知△AEF≌△AEF,从而可在Rt△DEF中得到结论EF 2=BE 2+DF 2成立.
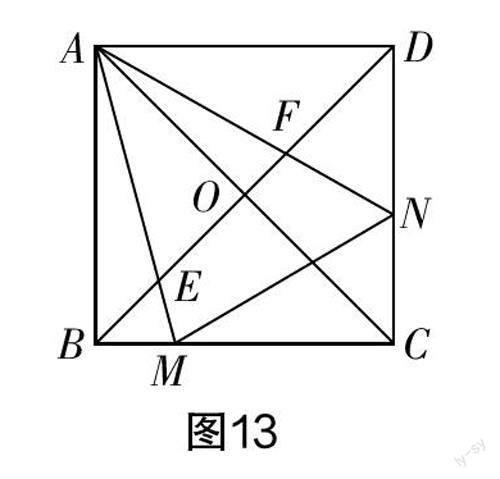
变式 在“问题2”的基础上,连接AC交BD于点O,如图13所示,求证:∠AMB =∠AMN =∠AFB.
分析 由解决“问题1”可得∠AMB=∠AMN,又∠AMB+∠BAM=90°,∠AFB+∠FAO=90°,∠BAC=∠MAN=45°,所以∠BAM =∠FAO,∠AMB=∠AFB. 问题得证.
5. 拓展挑战
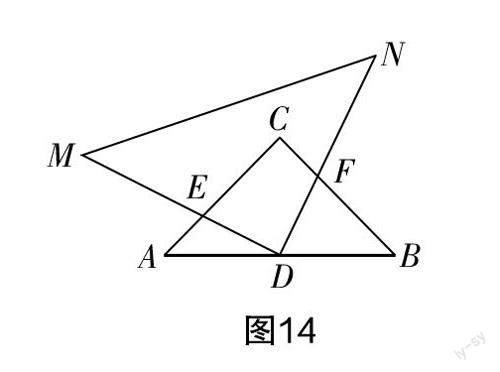
拓展 如图14所示,△ABC为等腰直角三角形,其中∠ACB=90°,AC=BC=2,D为AB边的中点. 将等腰直角三角板的直角顶点放置于点D处,两条直角边分别与△ABC的AC,BC边相交于点E和点F(点E不与C,A两点重合,点F不与C,B两点重合),求CE+CF的值.
分析 求CE+CF的值,跟引题求证MN=BM+CN和迁移运用求证MN=BM+DN类似,但又不同,前者求值,后者求证一个等式. 我们猜想,能否把CE,CF转化到同一条线段上呢?观察图形,可直观猜想将它们转化到线段BC上,又BC=BF+CF,于是只要说明CE=BF即可.
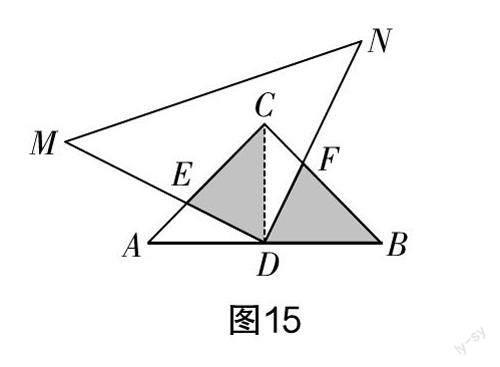
要证CE=BF,考虑到证明线段相等的方法,如全等、等角对等边,结合已知条件等腰直角三角形和斜边上的中点,不难作出如图15所示的辅助线,即连接CD,此时通过证明△DEC≌△DFB就可以了. 其实也可以看作将△DBF绕点D逆时针旋转90°后得到△DCE,从而得到结论.
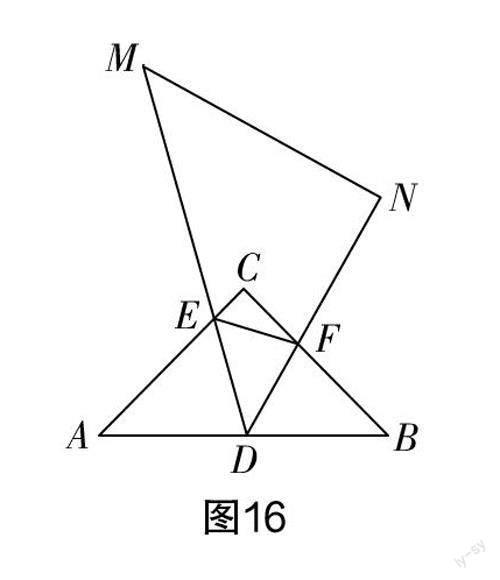
变式 如图16所示,△ABC为等腰直角三角形,其中∠ACB=90°,AC=BC=2,D为AB边的中点. 将等腰直角三角板(△DMN)的一个45°角的顶点放置于点D处,其斜边及一条直角边分别与△ABC的边AC,BC相交于点E和点F(点E不与C,A两点重合,点F不与C,B两点重合),连接EF,以点D为旋转中心旋转等腰直角三角板DMN,则△CEF的周长是否发生变化?并说明理由.
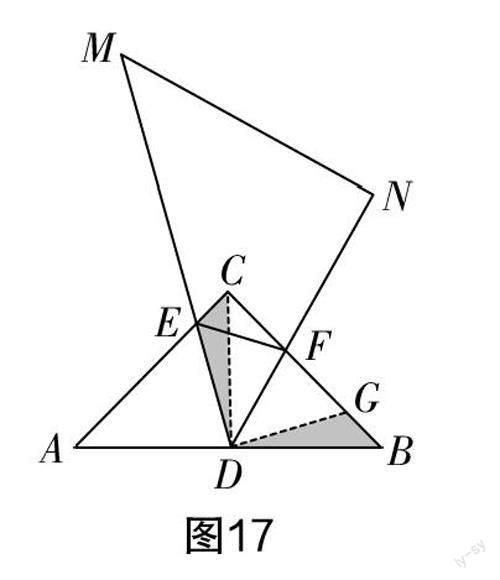
分析 求△CEF的周长,即求CE+EF+CF的值. 有了前面的解题经验,我们不难发现第一条辅助线,即连接CD(如图17所示). 再者,求几条线段的和,可以把这几条线段转化到同一条线段上,于是把△CDE绕点D顺时针旋转90°后得到△BDG,从而把CE转换成BG,这里其实只用过点D作DG⊥DE,交BC于点G,即得第二条辅助线,所以我们只需要证明△DEC≌△DGB(同上),△DEF≌△DGF即可. 所以CE+EF+CF=BG+FG+CF=2. 所以△CEF的周长不会发生变化.
教学思考
1. 优选引题,揭示问题本源
对于压轴题,学生望而却步,不假思索,“逃之夭夭”了. “截长补短”看似简单,但是遇到具体问题,不乏学生不识庐山真面目,甚至八、九年级的部分学生都不能很好地把握. 因此,教师要优选“引题”,有梯度地让绝大部分学生或多或少都能参与,并在解决“引题”的过程中,让学生自主观察、合作探索,提出各自添加輔助线的设想,并进一步探讨解决问题的方式方法,真正揭示问题本源,发现问题解决规律[3].
2. 注重通法,提升思维深度
本节课的教学聚焦三角形、四边形中几条线段间数量关系的研究,探索这类问题的本质规律和通性通法. 笔者从学生忌惮的问题(引题)出发,精讲细讲相对容易的第(1)问,让绝大部分学生“入戏”,从而发散学生的思维,让他们大胆猜想、发现解决问题的方法,让他们经历“探索方法—优化方法—反思方法”的过程,且他们反思后对方法的优劣进行选取,形成解决这类问题的通法,为后续解决第(2)问、第(3)问积累经验. 同时,也为后面的“迁移应用”和“拓展挑战”指引方向. 注重通法训练,构建知识体系,积累解题经验,提升思维深度,能让学习较困难的学生有所收获,能让大部分学生长本事,让优秀学生多赋能.
3. 拓展变式,发展数学素养
探究“引题”的价值不仅仅是让学生学习知识方法,更重要的是让学生学会灵活变通,触类旁通,有以不变应万变的能力. “拓展挑战”中的变式是求三角形的周长,其实还是探索三条线段的数量关系,虽然不是直接应用“截长补短”法,而是把几条线段转化到同一条线段上,但本质还是通过证明三角形全等实现转换. 学生根据“观察—探索—梳理”的解题经验,能从变化的图形中得到不变的结论. 所以,“拓展挑战”中的变式是让学生将所获得的知识、方法、经验进行融会贯通、举一反三,这能发展学生的数学素养.
参考文献:
[1]顾捷. 初中数学复习课教学的有效策略[J]. 开封教育学院学报,2014,34(12):239-240.
[2]吴凤. 初中数学复习课“一题一课”教学思路探微[J]. 基教与成才研究,2017(29):62.
[3]陆新锋. 聚焦主题精选学材,由浅及深渐次展开——以“线段之间数量关系”专题复习课为例[J]. 中学数学,2019(06):34-35.
作者简介:陈志婷(1988—),硕士研究生,一级教师,从事初中数学教学工作.

