基于多模型IMC-PID 的三水箱液位控制算法研究

徐 磊，吕 金

（天津电气科学研究院有限公司，天津 300180）

在工业生产中，液面高度是一个十分普遍的控制参量，具有观测方法简单、易于测定等优势。三容水箱系统作为一种具有大惯性、非线性和时滞性特点的液体水位控制系统，可以用来仿真并模拟石油化工、冶金和食品灌装等复杂的工业生产流程。因此，对三水箱的水位控制过程进行研究，不仅有现实的意义，而且具有良好的应用前景。为实现对三水箱液位的精准控制，有关单位在开展研究后提出了多种可用于三水箱液位控制的方法，但传统控制方法在应用后，不仅存在控制效果无法达到预期的问题，还会导致三水箱液位存在不稳定的缺陷。

陈玉华[1]在开展此方面内容的研究后，设计了一种针对液位控制的辅助装置，该装置中集成了高压加热器，可以操作此装置，实现对疏水液位的精准调控。以王超锋[2]为代表的多名科研人员在开展研究后，引进了改进差分进化算法，通过建立控制终端与计算机之间的通信连接，实现对液位控制方法的设计；完成设计后，将该方法应用到啤酒灌装机中，通过对啤酒灌装机在运行中PID 参数的整定，实现在机械操作中对液位的控制。

为发挥三水箱的更高效能，在开展相关研究后，本文将结合市场内现有的研究成果，引进多模型IMC-PID 技术，开发一种全新的液位控制算法，预期完成该算法的设计并将其正式投入使用后，可以实现对三水箱在使用中液位的精准调控。

1 基于多模型IMC-PID 的三水箱液位控制算法

1.1 基于多模型的三水箱模型结构设计

三水箱具备单容水箱和双容水箱的结构特性，因此在对三水箱模型结构设计前，需要明确单容水箱和双容水箱的基本结构。图1 为单容水箱基本结构示意图；图2 为双容水箱基本结构示意图。

图1 单容水箱基本结构示意图

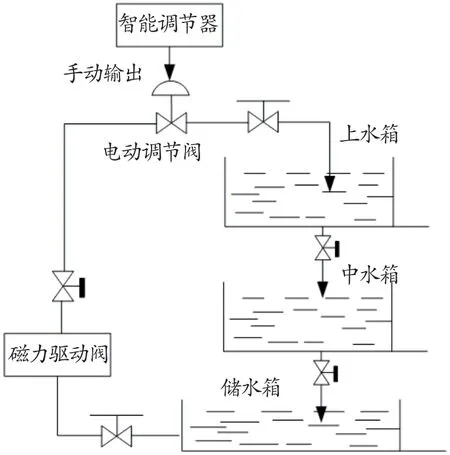
图2 双容水箱基本结构示意图

首先，针对图1 单容水箱结构进行分析，结合动态物料平衡的关系，得出下述公式

式中：Q1为上水箱进水口的流入量；Q2为出水口流出量；A 为上水箱横截面面积；d 为偏导数符号；h 为液位高度。

其次，结合图2 所示双容水箱基本结构，在模型中引入时滞项，即描述上、中双容水箱液位过程的二阶加时滞函数G（s）公式

式中：T2为第一个水箱的时间常数；T2为第二个水箱的时间常数；s 为时间；K2为双容水箱开环增益；L2为双容水箱的时滞时间。

最后，结合上述对单容水箱和双容水箱结构的分析，推导出三水箱模型结构公式

式中：L 为三水箱的时滞时间。

1.2 三水箱数据模型参数辨识

在完成对三水箱数据模型结构的设计后，对模型中的各个参数进行辨识。传统上，三水箱的数学模型参数的获得，通常是先对三水箱分别进行阶跃响应试验，再利用绘制的阶跃响应曲线，求出每个水箱的模型参数，最后把三水箱的模型进行乘积，就可以获得整个三水箱的数学模型[3]。对于模型的精度要求较低时，采用这种方法的确能够简便、快捷地获得三水箱的模型参数，但是对于较高精度的数学模型时，这种方法就不适合了。其不适合的主要原因是：利用绘图方法在阶跃响应曲线拐点上绘制切线以获取参数，需要非常高的精度，如果采集到的数据在阶跃响应曲线拐点上出现微小的偏差，则会造成利用绘图方法获得的系统参数出现较大的偏差。针对上述偏差问题，引入最小二乘法。该算法以错误的平方和最小为原则，为数据找到最优的功能匹配。用最小二乘法可简单地求出一个不确定的值，并使其与真实值的偏差的平方和达到最小值[4]。最小二乘方法原理简单，收敛速度快，易于理解，易于编程，因而被广泛地用于模型参数辨识。

针对上述构建的三水箱数学模型，将其转变为可以用差分方程描述的离散模型，将其采样周期设置为1 s，得到下述公式结果

式中：k、d、z 均为结构参数；y（k）为输入数据；u（k-d）为输出数据。

根据批处理最小二乘法定理可知，针对采样输入数据和输出数据，利用该算法可以得到模型参数向量的最小二乘辨识结果[5]。在确定各个结构参数后，只需要知道L 的取值，即可实现对三水箱数学模型参数的求解，通过观察实际获取到的输入和输出数据，从调节阀动作开始计时，观察水箱液位高度的变化情况，可以估计出L 的具体取值。

1.3 IMC-PID 控制器设计及参数整定

为实现对三水箱液位的控制，引入IMC-PID控制器。所选IMC-PID 控制器是带有滤波器的内模控制器，根据等效变换的原则推导得出相应的反馈控制器形式，进而得出等效PID 控制器[6]。结合上述三水箱数学模型，选择一个低通滤波器，该滤波器f（s）可以用下述公式表示

式中：λ 为滤波时间常数。设计一个带有滤波器的内模控制器，其表达函数公式为

式中：Q（s）为带有滤波器的内模控制器；M-1（s）为最小相位。

结合结构图等效变换原则，将典型内模控制结构图转变为等效经典反馈控制结构图，得到等效反馈控制器。设计的IMC-PID 控制器只与被控制参数K、T、L 以及滤波器的参数相关，而K、T、L为能够辨识出的固定模型参数。因此，只需要根据模型性能指标需求设定合适的滤波器参数，即可得到具备左右性能的IMC-PID 控制器。在此基础上，提出了一种IMC-PID 控制器的参数鲁棒调整方法，并通过实验验证了IMC-PID 控制器在一阶延迟过程中，既能保证最大敏感度又能保证系统的增益，同时还能保证系统的稳健性，建立了IMC-PID 控制器的可调参量与其最大敏感度的内在联系。通过鲁棒整定方法，使IMC-PID 控制系统中的最大敏感度指数M 成为唯一的可调节参量。最大敏感性指数M 可按要求在鲁棒性和动力学性能间进行权衡[7]。实验证明：M 的取数值太大，不仅会影响系统的鲁棒性，还会影响系统的动力学性能。因此，M 的取数值应控制在1～2 之间。为更好地决定IMC-PID控制器唯一可调节的参数M 的最优值，利用MATLAB 编程，将三容水箱的本地模式和相应的IMC-PID 控制程序编制成MATLAB，以1 s 的时间间隔，利用零阶保持器方法进行离散，以达到对三容水箱进行闭环控制[8]。观测不同M 取值对体系响应曲线的影响，实现对其动态控制。

2 实证分析

2.1 三水箱液位控制实验设计

相关研究至今，国内外众多的专家和技术人员都在积极地探索着各种新的液位控制方法，并为复杂的工业生产提供了一系列的解决方案。在现有的设计成果中，内模控制（Internal Model Control，IMC） 属于一种以过程数学模型为基础的新型控制技术。此项技术在应用中具有操作简单、便于计算和调节、鲁棒性强、适用于大滞后系统等优点。因此，多模型IMC-PID 被提出后，便受到工程界的广泛重视。在进行了大量的科学理论研究和现场实践测试之后，现已证实了多模型IMC-PID 可以实现对液位的精准控制。为进一步检验该方法的优势，将其应用到工程实例中，对其进行测试。

考虑在实际的控制过程中，三水箱液位经常会遇到许多不可预测的问题，如控制终端硬件的连接是否正确、控制过程中是否有信号的干扰、各部分硬件是否工作正常等问题，而这些问题的出现将会对最终的控制效果产生直接影响。为此在实验前，需要按照图3，建立控制终端与三水箱之间的良好连接，以此排除实验中外界因素与相关条件对液位控制效果的影响。图3 为实验终端连接硬件框图。

图3 实验终端连接硬件框图

2.2 实验现场调试

在对液位控制系统进行现场调试前，需要对控制系统中所涉及的所有硬件设备进行逐一调试，以保证所有硬件设备都可以正常、稳定工作。

确认了所有的硬件都已经准备就绪之后，根据本文所设计的三水箱液位过程控制，对有关的硬件设备进行正确的接线，并进行对应硬件设备接线的检查和校验，以保证接线的合理性和准确性。完成以上工作后，接通实验装置的电源，给装置上电。

打开由MATLAB 设计的控制软件界面，在相应的给定值栏中，可以随意地输入一个液位高度值。比如：先将液位高度值设置为75 mm，点击启动按钮；再运行控制程序，观察在控制过程中，系统的响应曲线是否为75 mm，如终端可以响应，即完成对实验环境中相关硬件设备的调试。

2.3 控制效果分析

设计三水箱液位控制值为165 mm，使用上文中设计的多模型IMC-PID 控制算法和传统PID 算法进行三水箱液位的调控，记录控制过程中三水箱液位-时间关系曲线。图4 为三水箱液位-时间关系曲线（控制效果）。

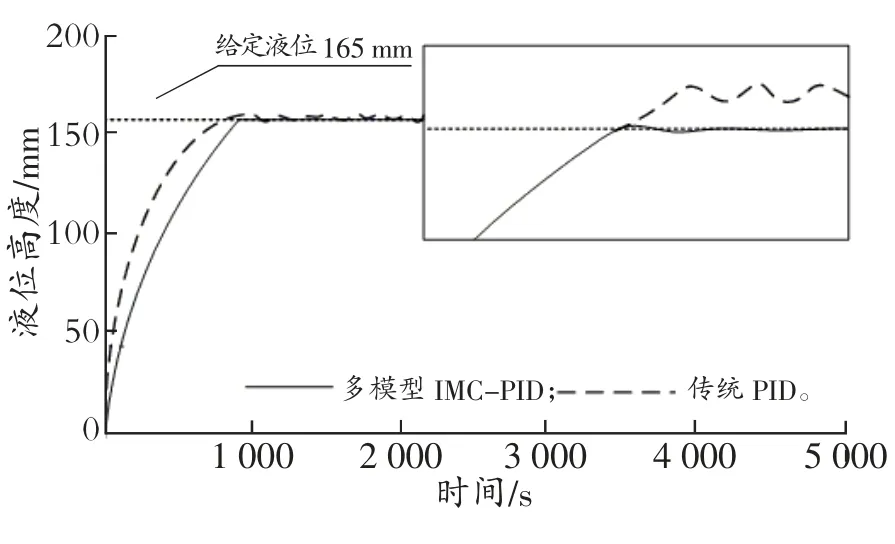
图4 三水箱液位-时间关系曲线（控制效果）

在上述内容的基础上，设计不同的液位控制高度，对比本文方法控制液位达到设计高度的时间与传统PIS 算法控制液位达到设计高度的时间。表1为控制时间对比表。

表1 控制时间对比表

3 结论

根据上述研究，得到如下结论。

参照图4 三水箱液位-时间关系曲线可看出，当设定三水箱液位高度为165 mm 时，多模型IMCPID 算法可以在一个相对较短的时间内，将三水箱液位高度稳定在165 mm。在对控制效果曲线分析中发现，传统PID 算法也可以实现将三水箱液位高度稳定在165 mm，但在稳定控制前，三水箱液位会经历一个相对较长的波动，即不稳定阶段。

综合表1 控制时间对比结果可知，在设计液位高度一致的条件下，多模型IMC-PID 算法控制时间＜传统PID 算法控制时间，说明在排除外界干扰的条件下，多模型IMC-PID 算法的控制效果更优，该算法可以在控制过程中，保证三水箱液位变化的平稳性，使液位快速处于稳态。

综上所述，本次设计的控制算法综合性能良好，具有代替传统控制算法在相关工程领域内推广使用的能力。