基于改进朴素贝叶斯分类算法的大学生综合测评预警研究*

魏 超

（陕西财经职业技术学院，陕西 咸阳 712000）

1 研究背景

党的二十大报告指出：“我们要坚持教育优先发展、科技自立自强、人才引领驱动，加快建设教育强国、科技强国、人才强国，坚持为党育人、为国育才，全面提高人才自主培养质量，着力造就拔尖创新人才，聚天下英才而用之”。学生是祖国的未来，如何培养出优秀的接班人是学校管理部门常思的一个问题，即如何激发每一个学生的学习潜能，为中华民族的伟大复兴贡献一份力量。大多数高校往往是用学生的历史考试成绩，计算概率或计数，从而对相应学生提出预警，但没考虑到在学生的学习过程中进行预警提示，以避免考试不及格，本文将坚持以人为本原则，以对学生和家长、学校、社会负责为出发点，以学习过程预警机制为研究视角，探索预警机制。

综合目前中国知网上相关研究文献，可分为两方面：一方面是对大学生综合素质进行综合评价研究，如谢国敏等[1]运用层次分析法（Analytic Hierarchy Process，AHP） 对大学生德智体三方面综合评价进行了研究；吴瀛灏等[2]对大学生综合素质评价指标进行了相关性分析和方差分析。另一方面是运用机器学习算法仅仅对高校学生学情进行研究，如吴鲲[3]运用机器学习技术包括随机森林算法、支持向量机和回归分类树等算法对学生成绩的预警系统进行建模研究；钟新成[4]运用朴素贝叶斯分类算法对高校学生学情进行预警分类研究。我国的教育方针是培养德智体美劳综合素质的人才，学习只是专业素质的表现，还需要结合德、体、美、劳四方面进行研究，基于培养德智体美劳综合素质人才目标，借助机器学习，以研究大学生综合素养的预警机制。

2 研究方法

本文借助于朴素贝叶斯分类算法，并进行算法改进，以研究大学生综合素质的预警机制。

2.1 贝叶斯理论

贝叶斯理论是在概率论的基础上提出的，包括先验概率、条件概率和后验概率等概念。条件概率是指在A 发生的条件下，B 发生的概率，也称为后验概率。假定A、B 两个事件，且先验概率P（A）＞0，则条件概率P（B|A）的表达式为

式中；P（AB）为联合概率，其表达式为

假设B1，B2，…，Bn是相互独立的，且其中任意P（Bi）＞0，则全概率的表达式为

那么，在A 发生的条件下，Bi发生的概率为

式（4）即贝叶斯公式。

2.2 朴素贝叶斯分类

朴素贝叶斯分类器（Naive Bayes Classifier，NBC） 也称为朴素贝叶斯分类算法，是一种常见的分类模型，数学理论基础扎实，具有可解释性强、模型处理过程简单和易于实现等优点，被广泛应用于实际社会现象中。基于贝叶斯理论，假设满足各属性相互独立的条件，可得朴素贝叶斯分类模型。设每个样本有n 个特征值，即用n 维向量表示X=[x1x2… xn]，样本数据中存在m 个类Y= [y1y2…ym]。通过朴素贝叶斯分类算法，可计算最大后验概率为

若式（5）满足设定样本所有特征属性相互独立，则求最大值。由于每个类在计算最大后验概率时，分母P（X）均为常数，因此求后验概率最大值，即求分子P（X|yi）P（yi）的最大值，朴素贝叶斯分类模型（目标函数） 表示为

式中：P（yi）为先验概率；P（xj|yi）为条件概率其中，先验概率P（xj|yi）的极大似然估计为

式中：N（yi）为yi类的样本总数；N 为总的训练样本总数。条件概率P（xj|yi）的极大似然估计为

式中：（yi，xj） 为yi类中存在特征属性xj的样本总数；N（yi）为yi类的样本总数。

由于实际问题中受样本个数限制，若某个特征属性值在样本训练集中没有与某个同类同时出现过，即可能出现式（6）中的条件概率为零，则导致连乘公式结果为零，其他特征属性取任意值都不能改变结果为零的结果，因此需要对朴素贝叶斯公式进行拉普拉斯平滑处理。平滑处理后的先验概率为

平滑处理后的条件概率为

式中：m 为样本在第i个特征属性上的取值个数。

2.3 加权朴素贝叶斯分类

朴素贝叶斯分类算法在假定所有特征属性相互独立，即条件概率相互独立时，隐含了另一个前提，就是各条件概率的权重相等，即每个特征属性对每个类的影响相同。但在实际问题中，每个特征属性对类的影响程度是不同的，因此需要对条件概率赋予不同的权重，以提高分类结果的准确性，即加权朴素贝叶斯分类[5]。本文将借用熵的概念，定义不同特征属性对分类的权重。

1948 年，克劳德·艾尔伍德·香农将熵的概念引入到信息论中。利用熵的原理确定指标权重的方法称为熵权法。熵权法根据指标的变异信息量确定权重。设有N 个样本数据集，n 个特征属性，形成原始指标数据矩阵X=（xki）N×n，对于某项指标xi，指标值xki的差异越大，则该指标在综合评价中所起的作用越大。

1） 对决策矩阵X 进行标准化处理，消除各指标量纲不同或数量级不同对评价结果带来的影响，从而形成标准化矩阵V=（vki）N×n。

2） 计算第i 项指标下，第k 个样本对象的特征属性比重

4） 计算第i 项指标的差异性系数di=1-ei。

因此，加权朴素贝叶斯分类模型（目标函数）表示为

3 实证分析

3.1 数据来源

本文大学生综合测评各项指标数据来自**学校，通过学校教务处、图书馆等部门取得2 000 名学生的调查数据，经数据清洗处理后得1 500 名学生的有效数据。借助加权朴素贝叶斯分类算法，以**学校为例进行大学生综合测评预警机制的研究。

3.2 大学生综合测评指标体系

基于培养德智体美劳全面发展的教育方针，从德育、智育、体育、美育和劳育五方面构建大学生综合测评评价指标体系，具体二级指标见表1。

表1 大学生综合评测评价指标体系

预警类别值为需要预警（Y1） 和不需要预警（Y2）。根据大二学生上学年的学习情况，收集以上所有指标样本数据。根据上学年德育成绩标记为德育是否需要预警，若德育成绩低于60 则标记为是（需要预警），否则标记为否（不需要预警）；根据上学年挂科门数标记为智育是否需要预警，若挂科门数大于等于3 门则标记为是，否则标记为否；根据上学年体测成绩标记为体育是否需要预警，若体测成绩低于60 则标记为是，否则标记为否；根据美育成绩标记为美育是否需要预警，若美育成绩低于60 则标记为是，否则标记为否；根据上学年参与劳动周得分标记为劳育是否需要预警，若劳动得分成绩低于60 则标记为是，否则标记为否。其中1 000 组数据用于进行模型训练，500 组数据用于模型测试。

3.3 大学生综合测评实证分析结果

根据加权朴素贝叶斯分类模型（目标函数），借助python 软件进行数据分析，其过程可描述为：首先，输入学生训练样本集N（D）=1 500、学生测试样本集N（T）=500、预警类别Y= [Y1Y2]，属性向量分别为A= [A1A2A3A4A5]，B= [B1B2B3B4B5B6]，C= [C1C2C3C4C5]，D= [D1D2]，E= [E1E2]；然后，依次统计N（Y1），N（Y2），qi，N（Ai，xi），N（Y1，Ai=xi），p（Y1|t），p（Y2|t）的值，将归为p（Yi|t）值最大的类别Y1；最后，输出正确率和计算时间。

运用k 均值聚类（k-means）[6]、朴素贝叶斯和加权朴素贝叶斯3 种分类算法，分别对高校学生的德智体美劳综合素质进行比较研究，对分类算法的评价指标包括正确率和计算时间。大学生综合测评、大学生德育、大学生智育、大学生体育、大学生美育、大学生劳育的各分类算法实验结果对比分别见表2～表7。

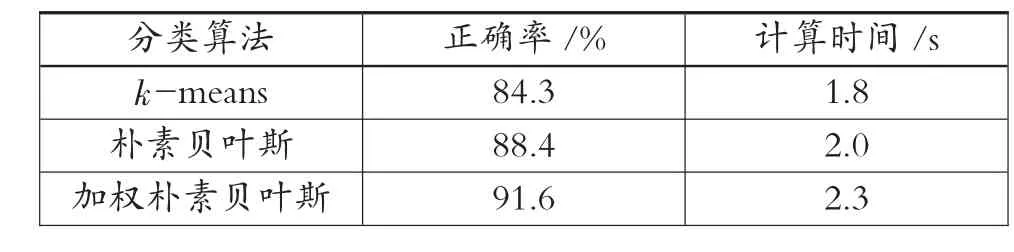
表2 大学生综合测评各分类算法实验结果对比表

由实验结果表2 可知，从正确率来看，加权朴素贝叶斯分类算法更优，获得了91.6%的正确率，而朴素贝叶斯分类算法和k-means 分类算法的正确率分别为88.4%和84.3%，均低于加权朴素贝叶斯分类算法。究其原因是加权朴素贝叶斯分类算法在朴素贝叶斯分类算法目标函数的基础上，赋予了一个权重系数，该系数体现了特征属性xi包含信息量的多少，熵值越大，则说明该特征属性对模型的贡献越大。而朴素贝叶斯分类算法是将在各特征属性相互独立的基础上建立的，忽略了各特征属性间的关联情况，比如网络游戏时间长，则晚自习的次数会相应会减少等。从分类算法计算时间来看，3 种分类算法计算时间相差不大，由于计算方法的复杂性，加权朴素贝叶斯分类算法需要2.3 s。

同理，由表3～表7 可以得知，从正确率来看，加权朴素贝叶斯分类算法更优，即加权朴素贝叶斯分类算法的正确率比k-means 分类算法和朴素贝叶斯分类算法的正确率都高。从计算时间来看，3 种分类算法相差不大，由于计算的复杂性，加权朴素贝叶斯分类算法时间相对略长。

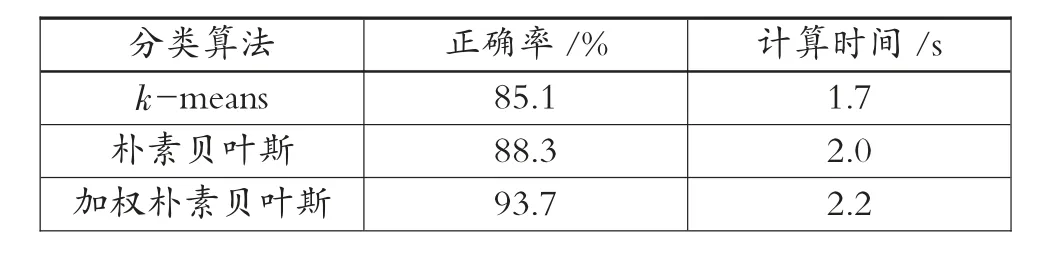
表3 大学生德育各分类算法实验结果对比表

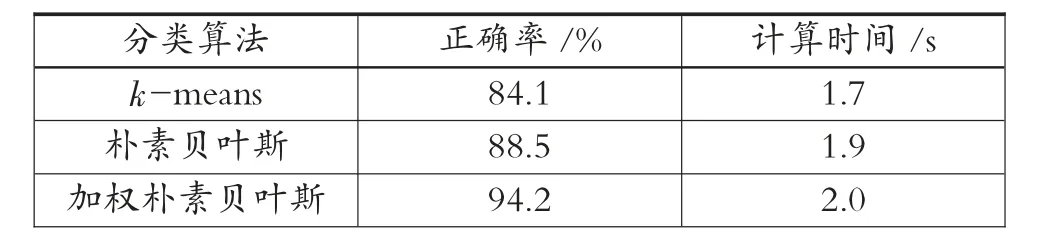
表4 大学生智育各分类算法实验结果对比表

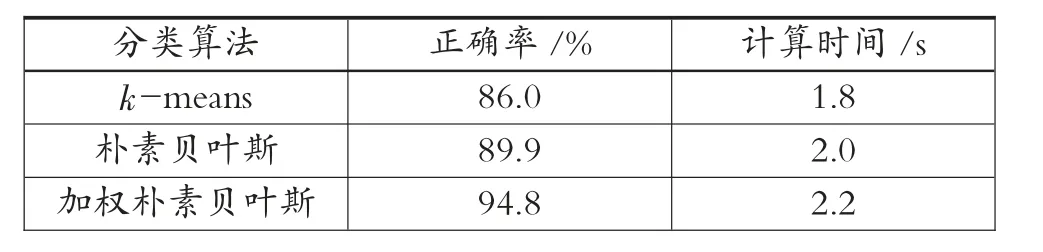
表5 大学生体育各分类算法实验结果对比表

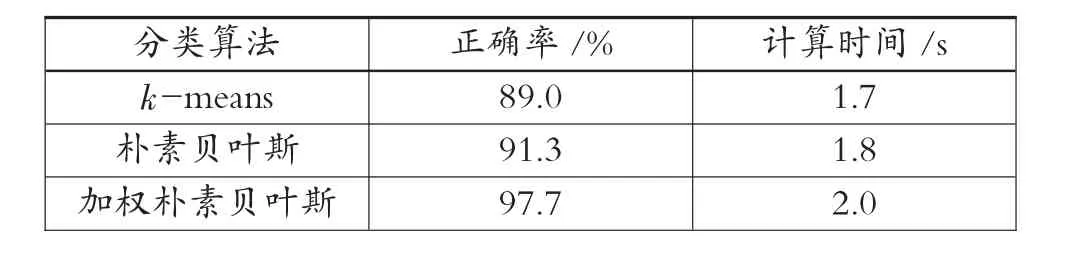
表6 大学生美育各分类算法实验结果对比表

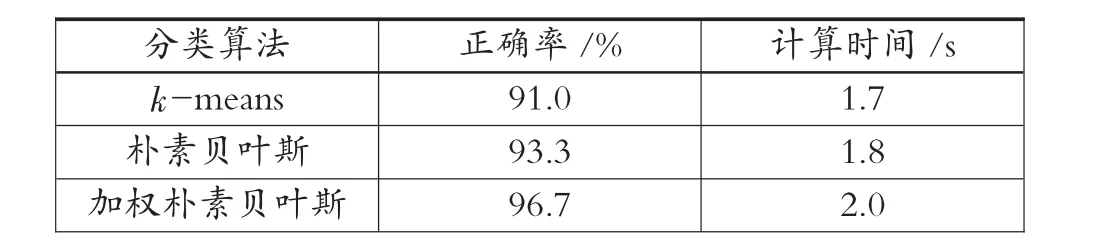
表7 大学生劳育各分类算法实验结果对比表

综上实验结果所述，综合正确率和计算时间的实验结果，加权朴素贝叶斯分类算法适用于对高校大学生综合测评预警，即进行综合素质预警和德智体美劳五方面分别进行预警效果较好。

4 结论与建议

通过加权朴素贝叶斯分类算法和k-means 分类算法、朴素贝叶斯分类算法的对比研究可知，由于在目标函数中给每个条件概率赋予了不同的权重，即不同特征属性对预警分类变量的重要性不同，从而加权朴素贝叶斯分类算法的正确率比其他两种分类算法都高，最终本文利用加权朴素贝叶斯分类算法实现了对高校大学生综合测评的预警研究。

该模型可用于高校教务处和学生管理部门对学生在校期间综合素质培养过程的监管和预警，从德智体美劳各方面进行具体指导。对于问题学生，可以提前进行提醒，将问题扼制在萌芽状态，避免出现预警或退学的结果，比如对于爱打游戏而缺乏自律的学生可以在学期中间进行预警，进而督促学生应该抓紧时间学习，以免期末考试不及格等。