无线传感网络误删数据匹配追踪恢复方法设计*

杨小琴，朱玉全

(1.南京工业大学浦江学院，江苏 南京 210000；2.江苏大学计算机科学与通信工程学院，江苏 镇江 212013)

无线传感器网络实质上是由带有计算、通信及存储功能传感器节点构成的分布式感知网络[1-2]。在信息技术日益完善的同时，计算机无论在生活中还是工作中都占据着不可或缺的地位，大量数据被保存到无线传感器网络中，这种保存方法虽然有着方便快捷的特点，但是当网络空间不足时，会导致部分数据被误删[3]，且这种问题是不可避免的，因此急需要一种对网络误删数据进行恢复的方法。

文献[4]提出了基于学习矩阵补全框架的无线传感器网络中鲁棒数据恢复方法。 采集无线传感器网络数据，使用少量接收测量的同时，恢复整个数据矩阵。 基于矩阵完成方法的新技术，接收到的读取矩阵包含与非活动节点相对应的多个缺失行，考虑节点间相关性的聚类技术，基于互补极小化问题的插值技术，保证了非活动节点读数的恢复。 通过实验验证了该方法具有一定的有效性。 文献[5]提出了改进压缩感知算法的WSN 数据恢复方法。 首先通过压缩感知算法，对无线传感网络中部分误删数据的节点进行恢复，利用原始数据节点以及恢复节点联合网络拓扑和数据骡子，将所有误删数据进行恢复，其次利用二次规划对访问失效传感器的邻居节点进行重构，实现无线传感器网络误删数据恢复。该方法的数据恢复所用成本较低。

虽然以上两种方法均能够有效实现数据恢复，但在对误删数据恢复过程中没有对误删数据进行定位处理，使得在恢复数据过程中加大计算量，导致出现数据恢复耗时长、数据恢复成功率低和特征拟合程度低的问题。 为了解决上述方法中存在的问题，提出基于匹配追踪的无线传感器网络误删数据恢复算法。

1 误删数据的迭代定位计算

由于无线传感网络会出现数据被误删的情况[6]，因此，为了精确恢复误删数据，首先设计匹配跟踪算法，对误删数据进行迭代定位计算，利用Gram-Schmidt 正交化方法，通过迭代生成新原子正交化，预测误删数据位置。

匹配跟踪算法[7-9]主要根据数据的稀疏度进行定位，匹配追踪算法是连续迭代的计算，每次迭代时原子字典D 会自动查找和残缺信号关联度最大的原子，经过不断地迭代，残缺信号的能量会渐渐下降，匹配追踪算法的特点就是每次迭代过程中都会选择和原始字典中残缺信号最接近的残缺信号，进而最大程度降低残缺信号的能量。

正交追踪算法主要利用Gram-Schmidt 正交化实现的，假设匹配算法中感知信号矢量为z，每次迭代计算时感知信号的正交投影过程[10]，即标准正交匹配过程的表达式为:

式中:Ds代表原子字典的系数向量，Ws代表相应支持集中的系数向量。

标准正交匹配算法[11]中需要对其中的最小二乘问题进行求解，因此需提前计算出向量Ds的伪逆进而得出式(1)的解，现已知当矩阵维度增加，伪逆的计算难度也会加强，为降低计算难度，需要使用QR 因子分解子字典，假设原子字典D中原子的QR 因子分解公式为:

式中:Dk代表原子字典D的列正交，Rk代表主对角线中存在正对角线因子的上三角矩阵，k代表迭代次数，λk代表正交矩阵。

令在迭代过程中选取的第i个原子为di，根据式(1)和式(2)更新出正交投影过程的计算表达式为:

根据Dk和λk的空间等价的特点得出RkWs＝ak，则式(3)变为如下公式:

根据QR 分解因子的特点得出的表达式为:

进而加快的求解速度，得出迭代后的最优解。

尽管不断降低计算复杂度，但是在不断更新正交矩阵λk以及Rk的过程中，迭代次数增加的同时三角矩阵的代价也会增加，所以需要通过正交化不断更新正交矩阵λk以此降低计算复杂度，因为原子字典中只有前k列才具有QR 分解，所以只有前k列才能分解λkRk，只需利用匹配算法过程查询λk的最后一列即可，进而得出λk，其表达式为:

式中:λk+1的计算公式为:

式中:λk代表λk匹配运算投影到张成空间(包含所有向量的线性组合所构成的空间)，dk+1代表原子字典中的原子，(ξ-λk)代表λk匹配运算投影到张成空间的正交补空间的分量，Pk+1代表原子的空间分量。

同理，根据正交标准化即可更新出三角矩阵Rk+1，矩阵的更新公式为:

式中:v和χ的公式分别为:

式中:v代表三角矩阵中的原子向量参数，χ代表常数项参数。

同理可知，计算出后，即可根据矩阵分块得出伪逆的三角矩阵的更新表达式:

利用匹配追踪算法，在误删数据定位的过程中不需要计算三角矩阵Rk，只需对λk和R-1k更新即可。 在定位过程中目标对象可能不在中心位置，这种情况下误删数据的相对稀疏信号为近似稀疏信号[12]，其中带有少量的非零元素，为了加强误删数据定位精度，利用质心算法[13]对稀疏向量w中的非零元素的目标信息进行处理。 假设第l个误删数据周围有e个点相应的值wl(i)，且每个误删数据相应的值必须大于阈值ϑ，进而得出所有格点的集合，其表达式为:

式中:i代表个点坐标的对应点。

所以利用集合sl的质心即可预测误删数据的位置，则误删数据的预测位置为:

式中:(xi，yi)表示第i个误删数据的位置坐标。

2 误删传感数据恢复问题转化计算

在通过迭代定位计算误删数据，预测到误删数据位置后，为了进一步加强数据恢复的准确性，基于时间稳定性的线性差值模型，估算出无线传感器网络中的误删数据值，将无线传感网络误删数据恢复问题转化为二次规划问题，通过迭代得出最终解，以此实现误删数据恢复。

假设在t个时间间隙的周期中，某个无线传感器收集到的感知属性为Gj＝((y1j，T1)，…，(ytj，Tt))，任意时间的误删感知值为ymj，当估算值与ymj之差最小，即可确定为最佳误差估计值。

通常情况下，在一个时间间隙中，感知数据[14]均是平稳的，可通过感知数据的时间稳定性建立分段线性函数，根据现有的数据点开展线性插值，进而估算误删数据。 令无线传感器网络中的某个节点为ni，当t时刻无线传感器网络出现误删数据时，根据其相近时刻Tiu的感知数据yiu和Tiv时刻的感知数据yiv建立出线性分段函数，其表达式为:

进而得出t时刻的误删数据估算值，其表达式为:

基于估算的误删数据进行数据恢复，通常情况下在误删数据恢复过程中会将其转换成1 范数最小化问题，但会在一定程度上忽略部分误删数据，所以需要将1 范数最小化问题再次转化成二次规划问题更加合理[15-16]，根据线性规划理论可知，当阈值κ≥0，此时的1 范数最小化问题的解为:

式中:τ代表伪随机序列构成的矩阵，y代表无线传感器节点收集数据与接收数据之间的联系，x代表无线传感器网络的数据变量。

假设变量分为正负两部分，将正变量标记为α，负变量为β，且两变量均大于等于0，则有界约束的二次规划问题的表达式为:

式中:I代表1 范元素集合，N代表元素数量，T代表误删数据监测的时刻。

表1 无线传感器网络硬件参数

进而得出无线传感器误删数据恢复问题转化成二次规划问题的标准公式:

式中:A代表伪随机序列集合。

运用阿米霍步长准则对式(17)进行求解即可得到误删数据。 即根据误删数据的定位和估算值计算出标量的初始值，其表达式为:

式中:g(k)代表定义向量。

通过初始化标量η0和参数φ构建出序列ι元素，其中参数φ∈(0，1)，凭借阿米霍步长准则的回溯线搜索将ι元素中的每种元素进行迭代到达标量η(k)的位置，直至最终的原子di+1大于前一个原子di，此时将标量η(k)的值进行记载。

完成上述操作后需要断定是否停止迭代，若迭代条件满足下列不等式，则停止迭代，并输出最终解:

式中:∇F(z)代表梯度方向。

则误删数据的最终解为:

若不满足，则重新计算标量的初始值，再以此进行迭代直至得出最终结果。

3 仿真结果与分析

为了验证基于匹配追踪的无线传感器网络误删数据恢复算法的有效性，利用MATLAB 软件对所提方法、文献[4]方法和文献[5]方法进行仿真，仿真结果如下所示。 为了证明所提方法的可行性，需要选取硬件数据支持，无线传感器网络硬件参数如表1所示。

3.1 数据恢复耗时

误删数据恢复对时效性的要求较高，部分数据仅在某一时刻时被利用，所以必须在最快时间内完成恢复，且保证恢复质量。

在上述仿真环境下利用三种方法对RAMCloud数据集群的误删数据进行恢复，设置不同成功率，判断每种方法恢复数据所需的耗时，对比结果如图1所示。

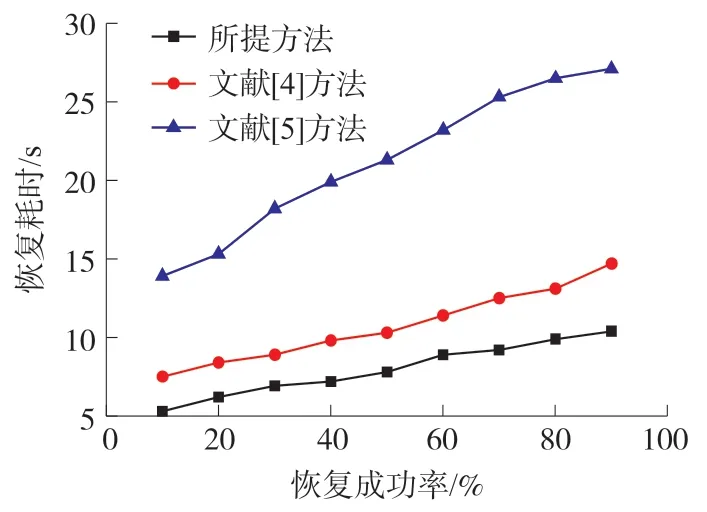
图1 不同方法的数据恢复耗时对比结果

根据图1 可知，随着恢复成功率的增加，不同方法的误删数据恢复耗时逐渐增加。 当恢复成功率为90%时，文献[4]方法和文献[5]方法的误删数据恢复耗时分别为14.7 s 和27.1 s，而所提方法的误删数据恢复耗时仅为10.4 s。 所提方法和文献[4]方法的耗时相近，但所提方法的用时更短，而文献[5]方法的耗时远远大于其他两种方法。 由此可知，所提方法的误差数据恢复效率高，时效性强。 这是因为所提方法对误删数据的位置进行预测，可减少最终的计算量，从而加快误删数据恢复时间。

3.2 恢复后数据与原始数据特征向量拟合程度

无线传感器网络数据是根据网络节点进行传输，会因为数据包所包含信息不同出现特征幅度值变化，以50 个节点为一个节点簇，将簇最完整的数据特征向量幅度值，与其余三种方法的复原后幅度值进行拟合，得出其中拟合程度最高的方法，即为最优方法，对比结果如图2 所示。

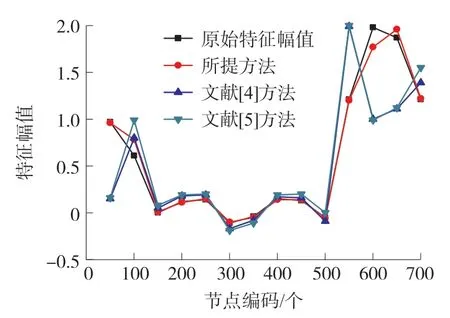
图2 不同方法的数据恢复特征向量的拟合程度

根据图2 可知，在700 个节点编码中，文献[4]方法和文献[5]方法的数据恢复特征幅值与原始特征幅值的最大误差分别为0.98 和0.99，而所提方法的数据恢复特征幅值与原始特征幅值的最大误差仅为0.21。 相比文献[4]方法和文献[5]方法，所提方法与原始数据传输过程中幅度值最接近。 由此可知，所提方法的恢复后数据与原始数据特征向量拟合程度较好，能够有效确保无线传感器网络关键数据的完整性。

3.3 数据恢复成功率

为了进一步验证所提方法的有效性，尽可能降低三种方法在仿真过程中的偶然性，选取15 组完全不同的仿真样本，并将其设置成编号1~编号15，每组编号中的删除数据位置不同且数量也不相同，使用信息熵作为验证指标，误删前每组信息熵均为1，在每组仿真下均用三种数据恢复方法对数据进行处理，对比结果如图3 所示。

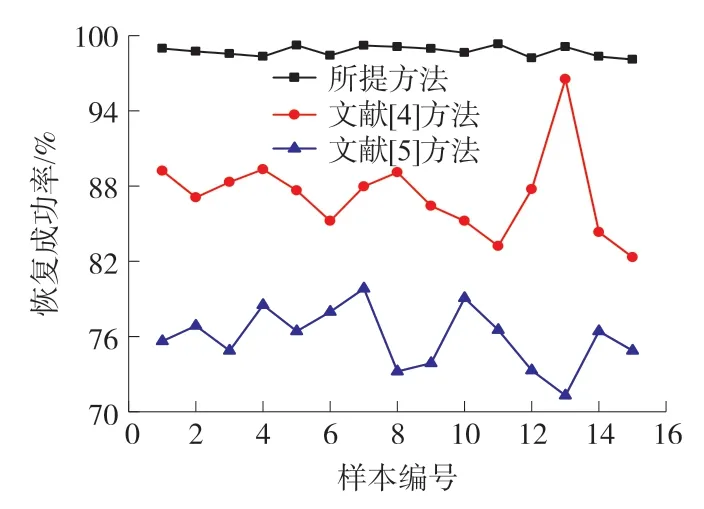
图3 不同方法的数据恢复成功率对比结果

根据图3 可知，当样本编码为15 时，文献[4]方法和文献[5]方法的平均数据恢复成功率为87.33%和75.93%，而所提方法的平均数据恢复成功率高达98.76%。 由此可知，所提方法的数据恢复能力较强。

4 结束语

随着无线传感器网络大规模的普及，其中不可避免出现误删数据，为此提出基于匹配追踪的无线传感器网络误删数据恢复算法，通过匹配算法对误删数据进行定位，并估算预测出粗略的误删数据，在二次规划问题的帮助下得出误删数据，实现无线传感器网络误删数据恢复，解决了数据恢复耗时长、数据恢复成功率低的问题，保证网络数据的时效性，也确保用户可以获取准确无误的数据。