基于图卷积神经网络的压缩机组风险预警模型
刘鹏涛
国家管网集团西部管道有限责任公司, 甘肃 兰州 730070
0 前言
近年来,为减弱以煤炭为主的能源结构体系对环境造成的破坏与污染,实现“双碳”目标,以天然气为主的清洁能源成为实现能源低碳转型的最佳途径。天然气的主要成分是甲烷,与其他燃料相比,天然气具有成本低、使用安全性高和环保价值较高的优点,被广泛应用于工业制造[1]、发电[2]以及城市生活燃气[3]等领域。从天然气的集中开采到使用的过程中,管道运输是天然气的主要运送方式,在管道中通过压缩机组对天然气进行加压,以额定压力连续平稳地将天然气交付给下游客户。作为管道运输的关键特种设备,压缩机组主要由压缩机体、润滑系统、密封系统和辅助系统组成[4],为天然气远距离传输持续提供压力保障。然而,由于天然气的高温、高压和易腐蚀等特征,压缩机组运行过程中极易发生故障,造成燃气泄漏、全线停输,甚至爆炸。研究表明,提前对压缩机组的关键信号量监测数据进行分析能极大降低风险和减少事故处理成本,建立可靠的模型进行预警分析已成为当前的研究热点[5]。
目前,常用的预警分析模型主要分为三类,即基于模式识别、模糊综合评估和深度学习。类似于机器学习,模式识别通过建立模型训练压缩机组的历史监测数据来预测当前机组的状态。Wang Jiangyu等人[6]通过分析历史监测数据的相关性进行特征提取,依据分类和回归树建立了机组故障检测决策树模型(Classification and Regression Tree,CART),当数据规模较大时,该算法模型取得预警效果并不理想。Li Guannan等人[7]通过支持向量数据描述(Support Vector Data Description,SVDD)的统计值判断数据样本是否出现在正常区域内,作为故障检测的依据,结合主成分分析(Principal Component Analysis,PCA)提出一种PCA-R-SVDD故障预警模型。Cui Chao等人[8]将PCA和反向传播相结合,对历史监测数据进行最优变量选择并构建动态记忆矩阵,提出简化的多变量状态估计(Multivariate State Estimation Technique,MSET)预警模型。Li Xiaochuan等人[9]通过皮尔逊相关系数分析历史正常数据和故障数据的区别,依据粒子滤波建立了增强代谢灰色故障预测模型。这些方法的共同点是通过故障数据训练模型参数进行故障预警,但压缩机组的故障数据样本数量较小,故障类别偏多,依据PCA和相关系数等多元统计分析方法进行深层次数据特征挖掘时故障预警的准确性表现较差[10]。
模糊综合评估是基于模糊数学原理,通过分析故障产生的各种因素建立评价指标来判别机组的运行状态。Gan Luping等人[11]考虑故障类别的相关性,通过整合故障关键性分析和故障树提出了加权模糊风险优先级数的评估方法,一定程度上从定性和定量两方面增强了压缩机风险评估的准确性。为缓解指标相关性对风险评估的影响,Sun Yanji等人[12]采用最大互信息系数消除高度相关的数据指标,通过二阶马尔可夫模型获得各个独立数据指标的预测值和优先级,再依据模糊隶属度加权法评估压缩机组的运行状态。Ge Haiyang等人[13]结合模糊层次分析法、模糊综合评价法以及增强故障模式效应分析,提出了基于增强故障模式效应分析的复杂系统风险评估模型。然而这些指标体系的建立过于主观并且无法有效评估复杂系统中的多种失效模式。
随着深度学习在图像识别、自然语言处理以及强化学习等计算机领域取得突破性进展,吸引了工控领域的大量学者展开了对深度学习的研究。Li Xiaochuan等人[14]依据环境和气体温度的历史监测数据,通过长短期记忆网络(Long Short-Term Memory,LSTM)预测进气温度,利用规范变量分析将进气温度的变化作为评判压缩机组运行性能的依据,虽然该方法有效预测了进气温度但仅利用温度的变化作为故障预警的依据并不可靠。Babu T N等人[15]通过傅里叶变换将轴承振动数据转化为频域信号,按振动信号的变化通过人工神经网络对压缩机组运行数据进行预警分析。为增强原始数据表示强度,Zhao Dongfang等人[16]将压缩机组振动数据转化为二维数据重排,结合注意力机制与卷积神经网络,提出了基于信号重排的机组故障诊断模型,但这些算法模型仅适用于单一信号量监测数据的故障预警。Qiu Jingwei[17]等人综合考虑压缩机组各子系统的监测数据,通过深度神经网络(Deep Neural Networks,DNN)学习到主要数据的特征表示,作为隐马尔可夫(Hidden Markov Model,HMM)的显性输入推断压缩机组的故障类型,提出一种基于DNN-HNN的故障预警模型,虽然结合考虑了子系统数据之间的关联性,但该方法过于依赖主特征对预警结果的影响。
现阶段,Tian Huixin等人[18]整合振动信号、温度、压力等多个参数信息,采用深度置信网络进行多维断层特征提取,之后依据特征提取结果构建健康曲线以此判断压缩机组运行状态,提出基于深度置信网络的时空特征融合故障诊断方法(Spatio-Temporal Features Fusion Based on Deep Belief Network,STF-DBN)。马海辉等人[19]依据傅里叶变化将压缩机组运行数据转化为频域特征,作为卷积神经网络(Convolutional Neural Network,CNN)的输入,输出层利用Softmax函数进行故障识别,压缩机组运行数据从时域到频域的转化,极大减少了人为提取特征的主观性。虽然这些方法在一定程度上取得了较好的预测效果,但并未考虑压缩机组系统中具有关联关系信号量作用下的隐含特征对压缩机组运行的影响。如压缩机的出口温度受动力涡轮转速、上游进口压力、进口温度、环境温度、润滑系统、密封系统、空冷等多种因素影响,这些信号量监测数据同时发生波动会使出口温度急剧增高或降低,如果不及时预警会造成压缩机组故障停机,影响上下游正常运输,甚至带来严重的社会和经济问题。此外,这些神经网络仅适用于具有一定规则的结构数据,对多信号量作用下的非欧结构数据并不有效[20];并且压缩机组站控报警系统仅在单一信号量超过设定值时才发生报警,对多因素微小故障影响下的隐含特征并不敏感。
因此,考虑多因素作用下的隐含特征对压缩机组运行的影响,通过图卷积神经网络(Graph Convolution Neural Networks,GCNN)对信号量的隐含特征进行特征提取,提出一种基于GCNN的压缩机组风险预警模型。首先将时序的信号量监测数据转化为基于时间点的信号网络,依据信号网络中节点之间的关联关系挖掘信号量的隐含特征;其次通过改进的密度峰值聚类(An Improved Density Peak Fast Search Algorithm,AIDP)算法,对信号网络进行故障粗分类,获得训练数据标签;最后通过GCNN学习标签数据的隐含特征,在输出层依据邻接矩阵进一步强化隐含特征表示,实现压缩机组风险预警分析。
1 相关工作
1.1 密度峰值聚类
密度峰值聚类(Clustering by Fast Search and Find of Density Peaks,CDP)算法是2014年发表在SCIENCE期刊上基于距离的聚类算法[21]。相比于其他类型聚类算法,CDP算法通过计算每个数据点的局部密度和最小距离能自动获取类簇中心;并且能够快速高效地聚类任意形状的数据点。由于易理解、易扩展和高效性等特征,该算法近几年来吸引了大量研究学者对其改进并应用到各个领域。
CDP算法的主要思想是通过计算任意两个数据点之间的欧氏距离得到截断距离dc,依据dc挖掘每个数据点的近邻,即局部密度ρi,考虑不同类簇数据点之间的最小距离δi尽可能大,同类簇数据点之间的δi尽可能小,以ρi为横轴,δi为纵轴构建决策图,依据决策图将ρi和δi较大的数据点作为类簇中心,最后将剩余数据点依据邻域分配到各个类中心所在的簇。
当数据点规模较大、类簇差异较小时,仅依据决策图并不能直观区分ρi和δi较大的数据点作为类簇中心[22];且CDP算法并不适用于无规则结构的非欧空间数据。本文通过定义信号网络的结构相似度,依据类中心值和类中心值变化率来自动选择聚类中心,提出了AIDP算法。
1.2 GCNN
目前,热门神经网络(如LSTM、DBN、DNN和CNN等)仅适用于具有一定规则的欧氏结构数据,如文本、图片、音频等。但在现实生活中,很多数据的结构特征表现为无规则特征,不满足平移不变性特征,如用户之间的链接关系组成社交网络、由知识图谱组成的语义网络等,这些神经网络并不能有效提取节点的特征表示。
GCNN由Kipf T等人[23]于2016年首次提出,依据傅里叶变换将非欧结构数据转化为谱域,通过拉普拉斯算子直接在谱域进行卷积操作,按特征表示类别被应用于非欧空间图结构数据的节点分类和图分类任务。基于谱域的GCNN特征传递方式描述为:
H(l+1)=σ(ϑH(l)W(l))
(1)
式中:H和H为特征矩阵,分别表示l层的输出和输入;ϑ=D0.5(A+I)D0.5为拉普拉斯算子,对应CNN的卷积核,A为邻接矩阵,I为单位矩阵,D为度矩阵,满足为l层的特征权重;σ(·)为激活函数,如(Relu)。
在进行特征表示的过程中,由于GCNN很大程度上能够保留信号量节点的隐含特征,本文通过GCNN训练节点的邻域获得隐含特征表示,以提高风险预警的准确性。
2 基于GCNN的压缩机组风险预警模型
为及时了解和掌握压缩机组运行状态,保障压缩机组安全平稳运行,通过分析压缩机组信号量历史监测数据,提出了基于GCNN的压缩机组风险预警模型,见图1。为挖掘多个信号量微小故障作用下隐含特征对机组运行的影响,首先时序信号量监测值转化为基于时间点的离散信号网络,之后依据AIPP算法对信号网络进行故障粗分类,获得训练数据标签,最后利用GCNN学习标签样本,充分挖掘信号量的隐含特征,实现风险预警。
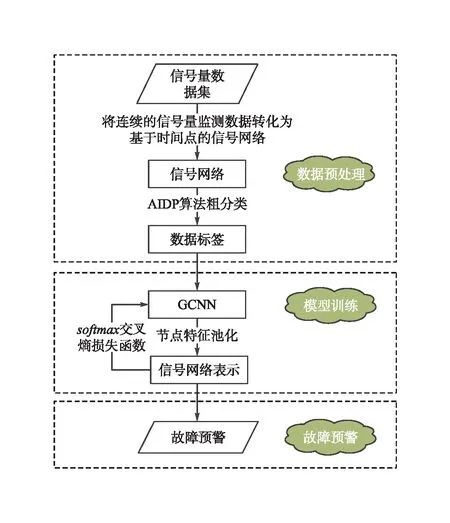
图1 基于GCNN的压缩机组风险预警模型图
2.1 SCADA监测数据的网络表示
由于数据采集与监控系统(Supervisory Control and Data Acquisition,SCADA)是以秒为单位获取压缩机组的信号量监测数据,这些数据存在大量冗余,极大地增加了计算复杂度。为降低冗余,本文将SCADA信号量监测数据离散化表示,创新性地给出了信号量数据集的定义描述。之后,考虑信号量之间的相关性,将信号量数据集转化为信号网络,利用边权重和边权重取值下限确定网络的复杂程度,通过挖掘网络中节点之间的潜在联系来获取信号量的隐含特征表示。
2.1.1 信号量数据集
在大量时序的SCADA数据中,以间隔5 s为基准取该段区间内数据的平均值,可以获得单个信号量精准的预测结果[24]。为了提升计算效率,通过这种描述方式,本文将时序的SCADA数据转化为离散信号量取值;同时,考虑信号量变化趋势的差异性和预警监测的及时性,将1 min内获得的12个区间离散值作为1组信号量样本。由此给出了信号量数据集的定义描述:给定m个SCADA信号量与n个时间点(1 min为1个时间点),信号量数据集描述为D=[S1,S2,…,Sn],其中Sn=[sn1,sn2,…,snm]表示第n个时间点内的m个信号量数据样本,snm=表示第m个信号量在第n个时间点内以间隔5 s为基准的监测平均值。
2.1.2 信号网络表示
压缩机组是由多个子系统组成的集成运行系统,各子系统的监测信号量之间存在复杂的关联关系,为挖掘信号量之间潜在联系对压缩机组运行的影响,本文将各时间点对应的信号量数据样本表示为信号网络。
在信号网络中,当信号量节点之间存在连边时,表明信号量节点之间的监测取值具有较强的相关性。此外,信号网络的复杂程度取决于节点之间的连边数量,连边数量越多网络结构越复杂,复杂的网络结构可以保留更多的信号量隐含特征,但计算难度增加;反之,能够提升计算效率,但保留的隐含特征较少。本文以信号量节点之间的相关性作为连边依据,通过边权重得到各个节点之间相关系数,之后引入F-score[18]作为边权重取值下限,以此确定连边数量。
(2)
(3)
综上,给定信号量数据集D,依据上述转化方式,与之对应的信号网络最终表示为三元组集合。
2.2 故障识别
现阶段,大多算法模型进行风险预警时主要考虑如何利用信号量监测数据构建精确的预警模型,但划分故障数据标签阶段的主观因素起主要作用。为此,提出了AIDP算法对各时间点内的信号网络进行故障标签粗划分,类簇的数量对应标签的种类,将故障标签作为GCNN的训练集,使得风险预警结果具有更高的可靠性和可解释性,所提算法包含关键步骤:将各时间点内的信号网络看作为AIDP算法的数据点;依据信号量在子系统内的相关性和子系统之间的相离性定义了信号网络结构相似度dGzGr;利用类中心值和类中心值变化率自动选择类中心点并划分故障类别。
2.2.1 AIDP算法描述
不同于CDP算法,AIDP算法数据点被描述为各时间点内的信号网络,并不能直接采用截断距离dc和局部密度ρi进行故障类别划分。为了正确识别不同时间点信号网络的故障类型,本文提出了dGzGr来替代dc,并重新定义了局部密度和最小距离。
(4)
局部密度表示信号网络的重要程度,最小距离表示信号网络在同一类别的可能性,通常需要构建以局部密度为纵轴,最小距离为横轴的决策图,通过综合比较局部密度和最小距离取值的离散程度确定合适的聚类中心点。为实现对各时间点内的信号网络进行故障标签粗划分,依据所提信号网络结构相似度,给出了局部密度和最小距离的定义描述。
ρGz=∑χ(dGzGr-dc)
(5)
(6)
(7)
然而,在聚类中心点选择过程中人为主观因素起决定性作用,一些复杂的决策图可能会造成聚类中心点的多选或少选[24],影响聚类结果的准确性。因此,本文引入类中心值ωGz与类中心值变化率rateGz来量化聚类中心点的选择条件,提出了一个较客观的解决思路。
ωGz=ρGz×δGz
(8)
(9)
2.2.2 AIDP算法流程
AIDP算法流程见表1。输入信号网络数据集,输出信号网络的故障类别。算法依次计算数据集中每个信号网络的局部密度ρGz与最小距离δGz,获得类中心值ωGz∈ωG,然后将整个数据集的类中心值ωG进行排序,依据类中心值变化率rateGz获得类簇中心,最后依据近邻距离对剩余信号网络划分类别。

表1 AIDP算法伪代码表
2.3 风险预警
本文利用AIDP算法实现了对各时间点的信号网络粗分类,即对不同时间点内信号网络进行故障识别,将确定为故障或非故障的信号网络作为GCNN的训练数据集。本节通过GCNN神经网络训练该数据集,学习各个信号网络中关联节点的隐含特征信息,以增强信号网络的故障表示,实现故障早发现,提高风险预警的准确性。
HGz=σ[ϑσ(ϑHGz(0)W(0))W(1)]
(10)
式中:H为输出层网络节点特征表示;W(0)、W(1)分别为第0层和第1层的权重矩阵。
GCNN输出层为节点的特征表示,即信号网络内单个信号量的隐含特征,为实现风险预警准确性,需要对输出层进行池化处理,以聚合信号网络中每个信号量的隐含特征,得到信号网络的网络特征表示。目前,常用的池化处理方法包含取最大值、取平均以及求和等,这些方法由于计算效率高被研究和学者广泛使用,但融合表示极易造成数据丢失,极大地影响预警准确性。为保留信号量节点更多的隐含特征信息,本文给出了新的节点特征池化表示方式:
oGz=AHGz·mean(HGz)
(11)
式中:o为经池化后的网络特征表示;A为节点的近邻矩阵。
在同一个信号网络内,由于近邻节点之间满足强相关性,将近邻节点视为具有较强联系的多个监测信号量集合,依据近邻节点之间的强相关性,能够增强网络故障特征表示,提升多个监控信号量微小故障对压缩机组运行的影响。
sGz=(s1,s2,…,sk)T=softmax(oGz·w+b)
(12)
同理,对于剩余网络,通过交叉熵损失函数不断重复上述过程,直到预测故障类别与真实标签之间的差异尽可能小,整个训练结束。
(13)
式中:stGz=表示信号网络Gz的真实故障分类,采用one-hot编码。当时,对于第k类,输出概率s越接近1时,模型越准确;当时,对于第k类,输出概率s越接近0时,模型越准确。
3 案例描述
3.1 数据预处理
选择某压气站场3台离心压缩机组运行数据作为实验数据集来验证算法模型的可行性,自投产以来,该压气站场的单台压缩机最大连续运行时间超过7 000 h。为便于分析和理解,通过所提出的模型对该压气站场典型的出口温度过高的异常事件进行风险预警,该事件主要原因是动力涡轮转速、上游进口温度和进口压力过高,次要原因包含润滑系统、密封系统、外界环境温度过高等。为提高风险预警的精确度,本文将异常事件发生前2 h和发生后5 min内的运行数据作为分析依据,得到包含128个SCADA监测信号量和125个时间点的实验数据集D128×125×12。
125个时间点对应的压缩机组出口温度、压缩机组动力涡轮转速、压缩机组进口压力、环境温度见图2。由图2-a)可看出,在121~125个时间点内,压缩机组出口温度较高,为异常事件发生之后的温度状态。由图2-b)、c)和d)可看出,第100个时间点之前的数据值都趋于平稳,当超过第100个时间点之后,动力涡轮转速、压缩机组出口压力、环境温度都有明显的变化。当时异常发生在夏季,环境温度处于上升状态,各影响因素使压缩机组进口压力处于下降趋势,加之动力涡轮转速提高,是造成此次压缩机组出口温度过高异常事件的主要原因。

a)出口温度
3.2 获得故障标签数据
依据所提信号量监测值的网络表示模型,获得了该数据集对应的信号网络表示,给出了AIDP算法对该数据集的聚类中心决策图,见图3。图3中每个数据点对应1个信号网络,数据点编号分别对应异常事件发生前、后的时间点,如第125个时间点表示事件发生后第5 min内的信号网络。由图3看出该数据集的类中心分别为85、121,数据点110具有较高的局部密度和最小距离,从决策图中并不能直观确定为聚类中心。因此,本文通过AIDP算法依据类中心值变化率确定85、121、110为聚类中心,分别对应正常运行信号网络、异常信号网络和类别不确定的信号网络,经过故障识别粗分类之后,获得了3种类别的信号网络数据集Dataset。
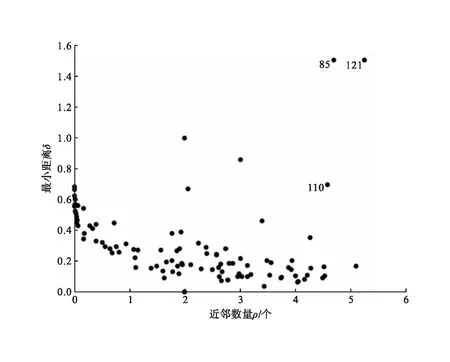
图3 AIDP算法聚类决策图
数据集Dataset包含101个正常运行信号网络、5个异常信号网络和19个类别不确定的信号网络,见表2。
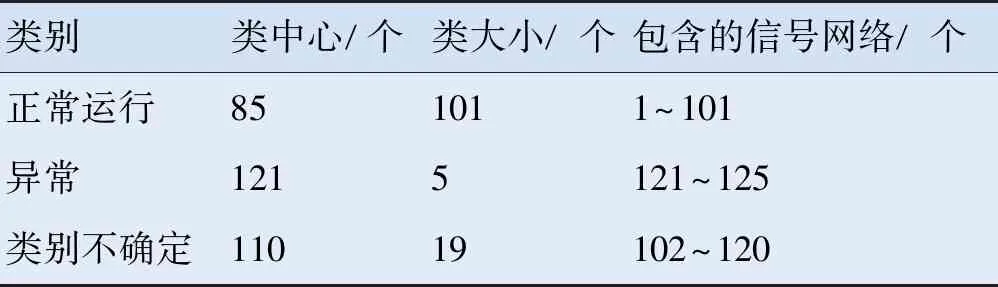
表2 Dataset数据集表
其中5个异常类为第121、122、123、124和125个时间点,都处于异常事件发生后的时间点内;正常运行类包含的信号网络,都处于事件发生前的时间点内,进一步表明AIDP算法对于故障识别具有极高的准确性。而对于最后一类,由于包含的信号网络所在时间点已非常接近异常事件发生时间点,此时动力涡轮转速、上游环境温度、进口压力和其他因素的信号量监测值不断发生波动变化,由于AIDP算法的信号网络结构相似度是依据信号量在子系统内的相关性和子系统之间的相离性来定义的,并不能有效识别多个监测信号量监测值波动引起的异常事件。之后将该数据集的正常运行信号网络和异常信号网络用于训练基于GCNN的压缩机组风险预警模型,通过模型对类别不确定的信号网络进行风险识别。
3.3 预警结果分析
将106个带标签的信号网络采用五折交叉验证划分为80%训练集和20%测试集两部分,来验证模型的准确性。训练集包含了82个正常运行信号网络和3个异常信号网络,验证集分别包含19个正常运行和异常信号网络,当训练集模型收敛时,验证结果中得到的正常运行与异常信号网络分别是19个、2个,正确率达到了100%,见表3。实验结果表明,本文模型对信号网络的异常识别具有非常高的准确性和鲁棒性,此外,采用交叉验证的方法能够更加有效地验证模型的性能,提高模型的可靠性。

表3 测试分类结果表
为验证模型的风险预警能力,通过训练106个带标签的信号网络,当训练模型收敛时,对125个信号网络进行结果验证,获得了125个信号网络的softmax所属类的概率值,风险预警结果见图4。从图4可看出,在0~114时间点内的信号网络属于正常运行类,从第115个时间点开始,对应的信号网络划分为异常类,比发生压缩机组出口温度过高的异常事件的发生提前了6 min,进一步验证了所提出的模型对风险预警的及时性和预警性。由于GCNN保留了信号量节点之间的隐含特征信息,通过训练节点表示,隐含特征信息将各微小的异常信号量逐渐放大,有效避免了平局池化后节点特征消失问题;所提出的模型在网络表示过程中,将近邻关系与节点表示再一次融合,进一步提升了多个相关联信号量节点的隐含特征对风险预警的影响,也规避了AIDP算法无法精确区分微小故障的问题。
3.4 参数分析
信号网络中,网络的复杂程度取决于节点之间的连边数量,连边数量越多网络结构越复杂,故障识别的准确度越高,但极大地增加了计算量;反之,网络包含的信息也就越少,对故障识别的难度随之增大。本文采用θvivj作为信号网络的边权重,节点之间关联程度随θvivj值减小而减小,确定合适的θvivj取值能够减少数据和冗余数据对实验结果带来的影响,提升故障分类的精准率。
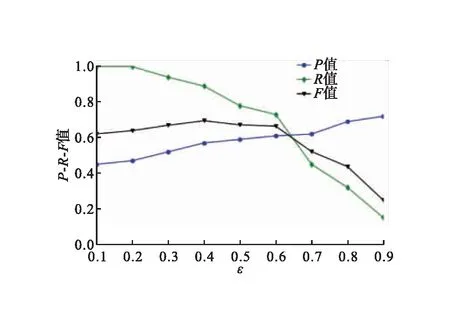
图5 边权重取值下限分析图
4 结论
压缩机组并不是一个独立的运行系统,而是由压缩机体、润滑系统、密封系统和辅助系统等多个子系统组成的复杂集成运行系统,各个子系统之间相互配合共同保障压缩机组的安全平稳运行。各子系统监测信号量之间存在复杂的关联关系,针对多监测信号量作用下隐含特征对压缩机组运行的影响,提出了基于GCNN的压缩机组风险预警模型。与以往风险预警方法不同,为了提取信号量监测数据的隐含特征,该模型将监测数据转化为基于时间点的信号网络,按AIDP算法对信号网络进行故障粗分类得到训练标签样本,通过GCNN训练标签数据的隐含特征实现压缩机组风险预报警。
对压缩机组出口温度过高异常事件进行实验预警分析,所提模型的故障标签识别率达到了100%;与事件发生时间相比,所提模型预测发生时间提早了6 min,极大增强了风险识别的准确性与风险预警能力,为事件的安全处理提供了充足的准备时间。在未来工作中,将重点关注所提模型对风险预警及时性和可靠性的研究,为压缩机组的可靠稳定运行提供安全保障。

