时延的事件触发无模型自适应抗干扰控制①

黄佳慧, 陆一凡, 沈 超, 陈 华

(1.河海大学理学院,江苏 南京 211100;2.河海大学商学院,江苏 常州 213022)

0 引 言

在许多实际系统中经常会遇到时滞和外部扰动,这会影响系统的控制性能,甚至导致受控系统的不稳定性。因此,研究这类具有时滞和外部扰动的非线性系统是一项重要而紧迫的工作。传统的控制算法,如Smith预测控制[1-2]、Dahlin算法[3-4],从理论上解决了时滞系统的控制问题。使用扰动观测器[5-7]估计外部扰动,有效处理扰动对系统带来的影响。但大多数算法依赖于受控对象的精确模型。然而,工业过程系统高度复杂,很难建立精确的模型。无模型自适应控制是一种仅依据非线性系统的输入输出数据,通过动态线性化方法设计控制器的智能控制方案。经过不断发展,无模型自适应控制的有效性已在自动驾驶汽车[8],交直流微电网[9]和压力系统[10]中得到验证。回顾现有关于无模型自适应控制方法的文献,针对时滞和扰动问题,文献[11]提出了一种具有扰动补偿的自适应跟踪控制策略,使非线性系统的跟踪误差收敛。文献[12-13]利用Smith预估器估计系统输出,并使用跟踪微分器获得预测器中的差分信号。上述研究只考虑了在时滞或扰动的情况下的控制算法。现有的研究很少同时考虑时滞和干扰。事实上,在工业控制过程中,大多数时滞和扰动同时存在。

综上所述,针对一类具有输入时滞和外部扰动的离散时间非线性系统,提出了一种改进的无模型自适应控制策略以跟踪期望的时变轨迹。此外,为解决数据传输过程中的通信带宽受限问题,设计事件触发条件以减少控制器执行次数。最后,运用压缩映射原理和Lyapunov稳定性理论证明了系统的稳定性。

1 问题描述

考虑一类含有输入时滞和扰动的离散时间非线性系统:

y(j+1)=f(y(j),…y(j-ny),u(j-τ),

…u(j-τ-nu),d(j),…d(j-nd)

(1)

其中,y和u分别表示系统的控制输出和控制输入信号,τ是时滞,d(j)表示有界扰动,满足|d(j)|≤bd;ny,nu和nd是未知的系统阶数;f(…)是未知的非线性函数。

假设1[14]：非线性函数f(…)关于其自变量的偏导数都是存在的。

假设2[14]：除有限时刻点外,离散时间非线性系统(1)满足广义的Lipschitz条件,即对任意的j1≠j2,j1,j2≥0,当u(j1-τ)≠u(j2-τ)时,有

|y(j1+1)-y(j2+1)|≤b|u(j1-τ)-u(j2-τ)|

其中,y(ji+1)=f(y(ji),…y(ji-ny),u(ji-τ),…u(ji-τ-nu),d(ji),…d(ji-nd)),i=1,2;b>0是一个常数。

假设1是非线性系统的常见限制。假设2是对输出变化边界的典型约束。许多实际的工业系统都满足上述两个假设,如温度控制系统、压力控制系统等。

根据假设1和假设2,离散时间非线性系统(1)可以转化为如下的等效数据模型

Δy(j+1)=φ(j-τ)Δu(j-τ)+αf(j-τ)

(2)

更进一步,可得

Δy(j+τ+1)=φ(j)Δu(j)+αf(j)

(3)

其中,

αf(j)=f(y(j+τ),…y(j+τ-ny),

u(j-1),u(j-1),…u(j-nu),d(j+τ),

…d(j+τ-nd))-f(y(j+τ-1),

…y(j+τ-ny-1),u(j-1),u(j-2),

…u(j-nu-1),d(j+τ-1),

…d(j+τ-nd-1))

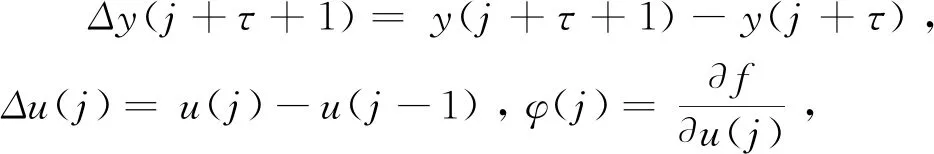
在实际应用过程中,数据在传输过程中通常会遇到通信带宽受限的问题。而事件触发控制是指满足预先设计的触发条件时,则更新控制输入;否则,控制输入保持不变。

本文的控制目标是设计一种适当的控制策略以驱动含有输入时滞和外界扰动的系统跟踪期望的时变轨迹。为了实现跟踪控制目标,运用离散时间扩展状态观测器估计残余非线性不确定项。此外,设计事件触发条件以减少数据传输,从而有效解决带宽受限的问题。

2 主要结果

2.1 基于离散时间扩展状态观测的无模型自适应控制

为了跟踪期望的时变轨迹,考虑如下准则函数:

J(u(j))=|yd(j+τ+1)-y(j+τ+1)|2+

λ|u(j)-u(j-1)|2

(4)

其中,λ>0是一个权重因子,用来限制控制输入的变化;yd(j+τ+1)是期望的输出信号。

将动态线性化模型(3)代入准则函数(4),并且关于控制输入u(j)求导使其等于0,则可得到控制输入算法:

y(j+τ)-αf(j))

(5)

其中,ρ∈(0,1]是步长因子,添加它可以提高控制方案的通用性。

由于控制输入算法(5)中含有未知的φ(j),并且φ(j)是一个时变参数,其精确值难以获取。因此,需要设计仅利用系统输入输出数据的估计算法以估计φ(j)。

为此,提出如下估计准则函数:

J(φ(j))=|y(j+τ)-y(j+τ-1)-

φ(j)Δu(j-1)-αf(j-1)|2+

(6)

其中,μ>0是一个权重因子。

对(6)关于φ(j)求极值,则可得到伪偏导数估计算法:

(7)

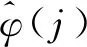
由于控制输入算法(5)和伪偏导数估计算法(7)中均含有未知项αf(j),利用扩展时间状态观测器估计残余非线性不确定项αf(j)。

定义新的状态向量Z(j)=[z1(j),z2(j-τ)]T=[y(j),αf(j-τ)]T,也就是说Z(j+τ)=[z1(j+τ),z2(j)]T=[y(j+τ),αf(j)]T。那么,动态线性化模型(3)可以写成如下状态空间形式:

(8)

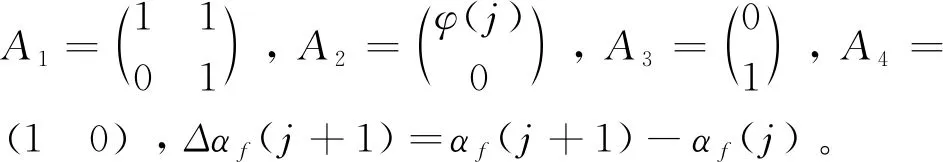
则系统(8)的离散时间扩展状态观测器可表示为:

(9)

因此,整个基于离散时间扩展状态观测器的无模型自适应控制方案的具体形式如下:

(10)

(11)

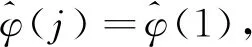
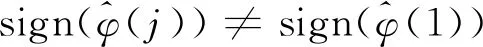
(12)

(13)

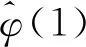
从(10)-(13)可以看出,所提出的控制方案仅仅使用闭环系统的输入输出数据,不需要受控系统的模型信息。同时,用离散时间扩展状态观测器估计的残余非线性不确定项在控制输入算法(10)中得到实时补偿。因此,该方案是一种数据驱动的抗干扰控制算法,可以保证系统的跟踪性能,具有较高的跟踪性能和较好的鲁棒性。

2.2 基于离散时间扩展状态观测的无模型自适应控制稳定性分析

假设3：对任意时刻j及Δu(j)≠0,系统的伪偏导数的符号保持不变,即满足φ(j)>κ>0或者φ(j)<-κ,其中,κ是一个小的正常数。

假设3意味着系统输出不应随着控制输入的增加而减少。这种特性在许多实际的工业系统中并不罕见,例如温度控制系统和压力控制系统。不失一般性,本文仅考虑φ(j)>κ的情况。

定理1：考虑满足假设1-3的系统(1),如果控制器的参数满足

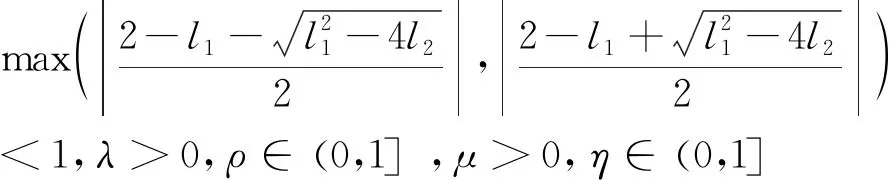
(1):随着时间的增加,离散时间扩展状态观测器是收敛的;

(3):系统的跟踪误差是有界收敛的。

如果选择合适的观测器增益,即

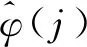
(14)

将动态线性化模型(3)代入(14),并且两边加绝对值,有:

|φ(j-1)-φ(j)|+

(15)

又μ>0和0<η≤1时,一定存在常数d1,使得:

(16)

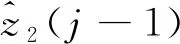
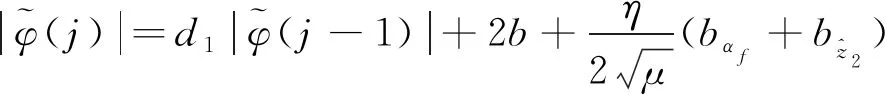
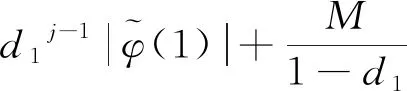
(17)

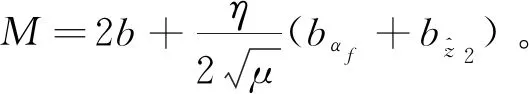
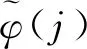
第三步：定义系统的跟踪误差:e(j+τ)=yd(j+τ)-y(j+τ)。当采样时间足够短时,假设yd(j+τ+1)=yd(j+τ)。那么,e(j+τ+1)可表示为:

e(j+τ+1)=yd(j+τ+1)-y(j+τ+1)

(18)

将动态线性化模型(3)和控制输入算法(10)代入(18),并且两边加绝对值,有

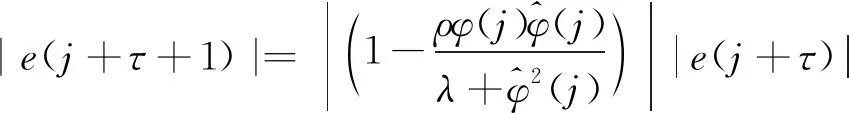
(19)

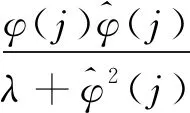
根据λ>λmin及0<ρ≤1,则一定存在一个常数d2,使得

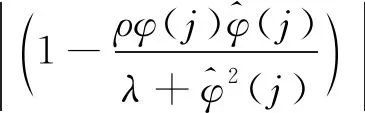
(20)

又根据期望的轨迹yd(j)是有界的,那么,存在一个常数使得|Δy(j+τ+1)|≤γ。此外,

(21)

结合(20)及(21),跟踪误差(19)可化简为:

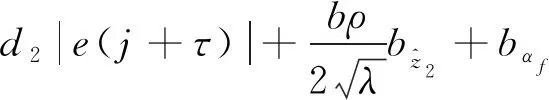
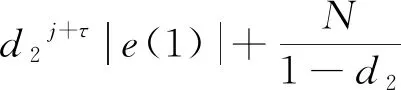
(22)

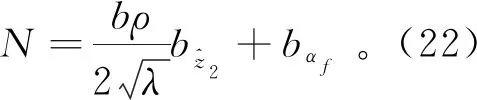
2.3 基于离散时间扩展状态观测的事件触发无模型自适应控制

在实际控制过程中,通常使用网络通信来传输数据,这不可避免地会遇到通信带宽有限的问题。应用事件触发机制来处理这个问题。为了清楚以下描述,触发的事件的时间序列表示为{ji},i=1,2,…。在事件触发机制中,只有当事件触发条件满足时,控制器才能接收到最新的采样数据,也就是说,只有当跟踪误差触发预先设计的阈值时,系统信息才会被发送。事件触发控制律如下:

(23)

定义事件触发误差σ(j)=e(ji)-e(j)。设计如下事件触发条件

(24)

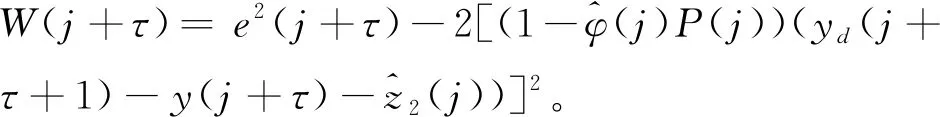
因此,整个基于离散时间扩展状态观测器的事件触发无模型自适应控制方案可以总结为:

(25)

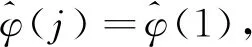
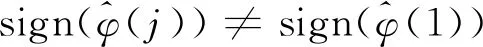
(26)

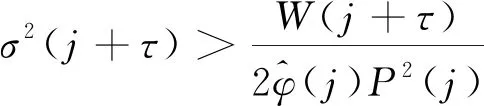
(27)

(28)

(29)

这里使用伪偏导数估计算法(25)与设计的事件触发定律(28)相结合,在线估计动态系统的参数,以实时应对不确定性。

2.4 基于离散时间扩展状态观测的事件触发无模型自适应控制稳定性分析

定理2：考虑满足假设1-3的系统(1),如果选择合适的参数并且使用事件触发无模型自适应控制方案(25)-(29),其跟踪误差是渐近收敛的。

证明：鉴于动态线性化模型(3)可知系统的跟踪误差为:

e(j+τ+1)=yd(j+τ+1)-y(j+τ+1)=

yd(j+τ+1)-y(j+τ)-φ(j)Δu(j)-αf(j)

(30)

在事件触发时刻,即j=ji时,根据控制输入算法(28)和离散时间扩展状态观测器,则(30)变为

e(j+τ+1)=(1-φ(j)P(j))(yd(j+τ+1)-

(31)

定义Lyapunov函数:V(j)=e2(j)。则

ΔV(j+τ+1)=[(1-φ(j)P(j))(yd(j+τ+1)-

(32)

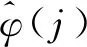
(33)

由于事件触发的误差是σ(j)=e(ji)-e(j),很明显可知在事件触发时刻σ(ji)=0。然后,根据事件触发条件(24),有

(34)

此外,根据(34)式,可以导出以下不等式

(35)

根据(33)式和(35)式,可以得到ΔV(j+τ+1)≤0。这也就是说,在所有触发时刻,所设计的事件触发无模型自适应控制可以使跟踪误差渐近收敛。

在事件不触发时刻,即j∈(ji-1,ji),在这个时间间隔内的控制输入与上次触发时刻的控制输入保持相同。显然,当控制输入保持不变时,系统保持稳定。

3 数值仿真

为了进一步验证所提方法的有效性,对其进行了如下模拟。值得注意的是,类似于系统结构、系统的阶数等系统的模型信息在控制方案中没有用到。下面例子中给出的系统模型仅是为了产生系统的输入输出数据,不参与控制器的设计。

考虑如下含有输入时滞和外部扰动的离散时间非线性系统:

离散时间非线性系统的期望输出轨迹是:

yd(j+1)=

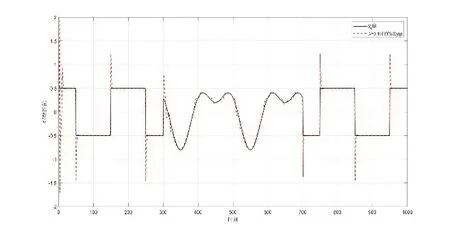
图1 无模型自适应控制的跟踪性能

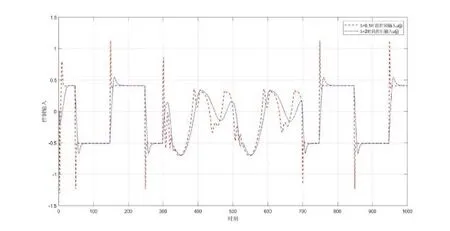
图2 无模型自适应控制的控制输入变化

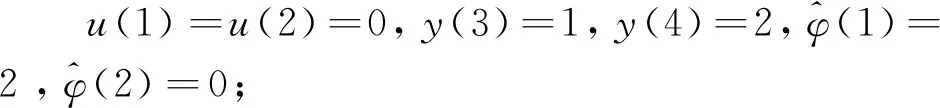
图3 无模型自适应控制的伪偏导数估计值

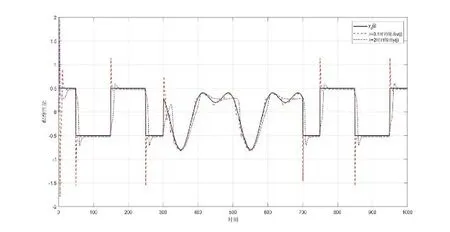
图4 事件触发无模型自适应控制的跟踪性能

仿真结果如图1-3所示,分别展示了权重因子λ=0.1及λ=2时的跟踪性能、控制输入和伪偏导数估计值。从图1可以看出,当λ=0.1时系统反应更快,能更好地跟踪上期望的时变轨迹。在图2中发现系统的控制输入是有界的。从图3可以看出,伪偏导数是一个慢时变的有界参数。

图4展示了使用基于离散时间扩展状态观测器的事件触发无模型自适应控制的跟踪性能,我们可以看出能跟踪上期望的轨迹,并且通过设计事件触发条件,控制器执行次数会减少,以有效解决通信带宽受限的问题。

4 结 语

针对一类具有时滞和有界扰动的离散时间系统,提出了一种改进的无模型自适应控制策略。首先,应用基于紧格式动态线性化的参数估计算法离线识别输入和输出数据的数据模型,然后将识别出的参数合并到无模型自适应控制算法中,实时更新线性模型。其次,设计了一个离散时间扩展状态观测器来估计未知的残差非线性时变项,该项被认为是一个新的状态。此外,设计了事件触发条件,以减少执行次数,有效解决通信带宽问题。最后,通过结合离散时间扩展状态观测器估计,分别提出了基于离散时间扩展状态观测器的无模型自适应控制和基于离散时间扩展状态观测器的事件触发无模型自适应控制。通过严谨的理论分析和数值仿真验证了所提出方法的有效性。