基于三坐标测量仪齿轮测量误差补偿的研究①

邹华兵

(湖南理工学院机械工程学院,湖南 岳阳 414000)

0 引 言

齿轮的精度检测是保证齿轮加工质量的前提。与激光干涉仪等精密的可用于运动平台检测的仪器相比,三坐标测量仪在测量效率方面具有明显的优势[1]。但随着先进制造技术的发展,使得对齿轮的加工精度要求越来越高,这为如何提高齿轮加工机床的加工精度和三坐标测量仪的测量精度提出了新的挑战。

几何误差和热误差往往是影响设备运动精度的主要因素[2],占误差总量的68%左右[3]。而三坐标测量仪仅被用于工件精度检测,发热量极少,几何误差便成为了影响其测量效果的主要因素。误差补偿技术是能够提高三坐标测量仪测量精度的一种既经济又非常有效的方法[4]。但与普通的数控系统相比,三坐标测量仪的运动精度更高,使得用于普通数控机床的几何误差模型难以适应三坐标测量仪测量误差精密补偿的需求。因此,研究精密的几何误差模型是实现三坐标测量仪测量误差精密补偿的关键。

1 三坐标测量仪的单轴运动模型

以三坐标测量仪Z轴方向的运动平台为例。三坐标测量仪的Z轴运动会产生6项几何误差[5-8],分别是绕X轴方向的旋转误差φx(Z)、绕Y轴方向的旋转误差φy(Z)和绕Z轴方向的旋转误差φz(Z),以及X轴方向的线性误差δx(Z),Y轴方向的线性误差δy(Z)和Z轴方向的线性误差δz(Z)[9-13]。根据齿轮的结构特征和需要测量的精度,可将X轴和Z轴视为精密运动轴,而与齿轮轴平行的Y轴视为普通运动轴。

1.1 Z轴与X轴的运动模型

三坐标测量仪Z轴运动平台的几何误差模型可表示为式(1)[14]:

(1)

式(1)中,

同理可知,三坐标测量仪X轴运动平台的误差变换矩阵如式(2):

(2)

式(2)中,

1.2 Y轴的运动模型

三坐标测量仪Y轴运动平台的误差变换矩阵如式(3):

(3)

2 三坐标测量仪普通的几何误差模型

三坐标测量仪作为典型的FXZY型数控系统,如图1所示。根据该三坐标测量仪的结构特点,其拓扑结构可以描述为图2所示。

图1 三坐标测量仪

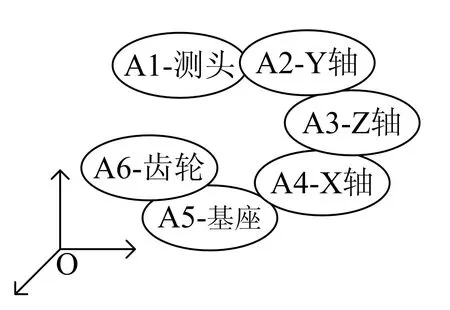
图2 FXZY型三坐标测量仪的拓扑结构

根据图2的描述,可得A5到A4的坐标变换矩阵为式(4):

(4)

公式(4)中,φxy为X轴与Y轴间的垂直度误差。A4到A3的坐标变换矩阵为式(5):

(5)

公式(5)中,φyz为Y轴与Z轴间的垂直度误差。A3到A2的坐标变换矩阵为式(6):

(6)

从A2运动到A1的坐标变换矩阵为式(7):

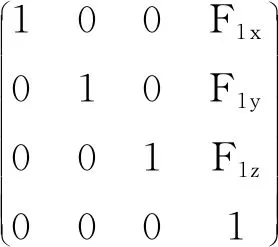
(7)

从A5运动到A6的坐标变换矩阵为式(8):

(8)

则三坐标测量仪普通的几何误差模型可以描述为式(9):

(9)

式(9)中,(Fkx,Fky,Fkz)(k=1,6)是在相应运动链之间的位置坐标矩阵。坐标(xc,yc,zc)和(xw,yw,zw)分别是测量点在测头坐标系和齿轮坐标系中的坐标。

3 三坐标测量仪精密的几何误差模型

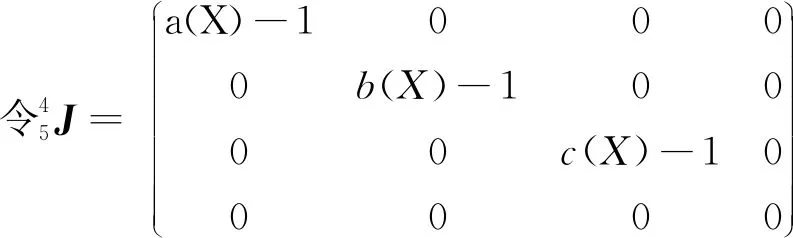
(10)

(11)

那么三坐标测量仪精密的几何误差模型可以描述为式(12):

(12)

采用激光干涉仪,测量出三坐标测量仪运动时的各单项几何误差[15],再将其分别带入精密的几何误差模型并计算出齿轮所需测量点的几何误差。最后将三坐标测量仪的测量值与相应点几何误差的计算值相加减,从而实现三坐标测量仪齿轮测量的误差补偿。

4 结 语

齿轮的精密检测是保证齿轮加工质量的前提。三坐标测量仪与可用于运动平台检测的激光干涉仪等精密仪器相比,在测量效率方面具有明显优势。与普通的数控机床相比,三坐标测量仪的运动精度更高。若选用普通的几何误差模型对三坐标测量仪的测量误差进行补偿,其补偿效果显然不佳。为适应三坐标测量仪测量误差精密补偿的需要,通过对影响齿轮测量误差的主要运动轴的几何误差模型进行了精算,建立了三坐标测量仪测量误差补偿所需的精密几何误差模型。