悬吊式换流阀塔设备一种滑动摩擦型减震系统的性能研究①

余佳琳, 吴 倩, 钱 江,*

(1.中国电力工程顾问集团华东电力设计院有限公司,上海 200063;2.同济大学土木工程学院结构防灾减灾工程系,上海 200092)

0 引 言

特高压直流输电具有线路损耗低、电压等级高、可控性强等优点,特别适合千公里级以上远距离电力输送[1]。我国是世界上特高压直流输电网络应用最广的国家[2]。电力系统一旦遭受地震破坏,其影响是灾难性的,不仅严重影响域内民众的生产、生活,而且高昂的维修、重建费用都将使国家财产受到巨大损失。作为特高压直流输电系统核心设备的悬吊式换流阀主要由瓷质晶闸管和电抗器组成,极易受震损坏,换流阀结构抗震问题一直是业界关注的热点问题。

国外在悬吊式换流阀塔的抗震研究方面起步较早,但囿于商业保密,有关阀塔柔性避震措施的技术细节均未公开[3,4]。国内学者吴小峰等[5]对单塔换流阀结构进行了有限元分析,认为换流阀在地震作用下的水平位移响应过大,应在设计研究中予以考虑。在减震措施研究方面,刘爱国等[6]在悬吊式绝缘子与阀层连接处增设铰接旋转刚度,以此降低阀体振动最大位移。杨振宇等[7]提出了使用张拉绝缘子将阀塔底部与地面拉结,并在接地处设置弹簧—阻尼器的方案。计算模拟结果表明可以减小60%的阀体水平位移响应。在阀体结构上增设附加弹簧虽然有可以达到减小响应位移的效果,但或多或少将影响到换流阀的电气性能或设备安装场所的自由空间。

提出一种利用设备悬吊点设置轨道滑动摩擦阻尼实现系统减震的新方法,将悬吊式换流阀结构简化为二自由度动力系统,通过能量原理建立力学简化系统的运动方程,给出了运动方程解析解的推导。分析了系统在谐激励下幅频响应曲线的特征,讨论了系统各参数对响应幅值的影响规律以及实现系统减震的参数取值范围。

1 计算模型

1.1 悬吊式换流阀结构特征及轨道滑块系统

如图1所示,某特高压直流输电网络±800KV换流站典型的悬吊式换流阀塔由阀模块、上下屏蔽罩、避雷器等部件组成,阀模块之间由层间绝缘子连接,顶部由悬吊绝缘子连接到阀厅横梁上。阀塔总重14.5t,阀塔设计总高13.5m,顶部悬吊绝缘子长6.5m。其水平运动以质心绕悬吊点摆动为主,故可简化为一悬吊长度为10m的单摆。

图1 悬吊式换流阀结构图示

为控制单摆振动幅值,在悬吊点设置如图2所示轨道滑块摩擦阻尼系统,当滑块运动到轨道上某一点时,产生的水平向回复力不仅和质量块的运动状态(位移、速度、加速度)有关,还取决于该点的轨道形状。因此,可以通过改变轨道形状得到不同的力—位移关系,进而调控单摆的运动状态。

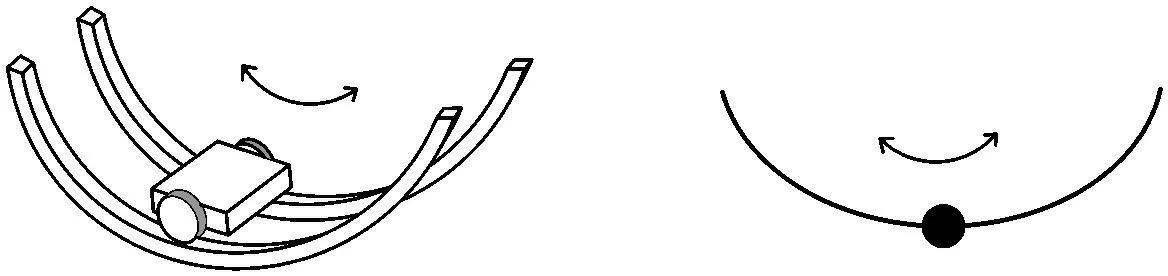
图2 轨道滑块摩擦阻尼系统示意图

1.2 简化力学模型及系统运动方程型

将图1及图2组合后形成一个悬吊点可沿轨道滑动的单摆系统,轨道形状可调,且考虑滑块与轨道间的滑动阻尼,得到图3所示的简化力学模型。

图3 简化力学模型

图3中各参数含义如下:

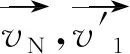
1.3 系统的运动方程

运用拉格朗日方程法对图3所示的简化力学模型进行运动分析。

系统动能:

(1)

系统势能:

V=mNgyN+m1g(l-y0)

(2)

非保守力虚功:

(3)

由几何关系:

(4)

(5)

tanφ=dy/dx=h′(xN)

(6)

故:

(7)

由几何关系:

(8)

(9)

(10)

故:

(11)

(12)

整理式(1)、(7)、(12)得系统总动能:

(13)

由几何关系:

(14)

整理式(2),(14)得系统总势能:

V=(mN+m1)gh(xN)+m1gl(1-cosθ)

(15)

由几何关系:

(16)

整理式(3)、(7)、(9)、(16)得非保守力虚功:

(17)

故阻尼引起的非保守力:

(18)

(mN+m1)gh′(xN)=0

(19)

(20)

由轨道形状对称并足够光滑,且y(0)=h(0)=0,将h(xN)在xN=0处展开成泰勒级数形式,有:

(21)

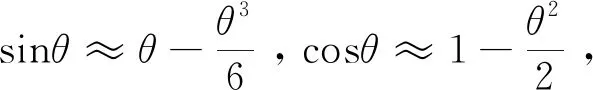
保留至一阶小量,得二自由度系统运动方程:

(22)

2 运动方程的求解

(23)

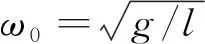
(24)

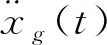
(25)

解得:

(26)

式(26)中,Δ(ω)为系统的特征多项式:

(27)

Δ(ω)=0即为系统的特征方程,解此方程得可能的实数根:

(28)

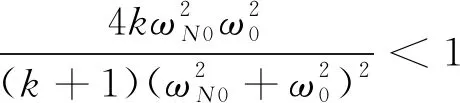
记系统的幅频响应函数为F(ω),有:

F(ω)=

(29)

滑块及单摆质点的响应振幅比可写成:

(30)

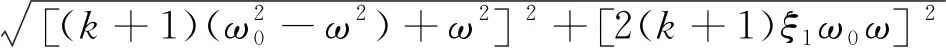
(31)

3 系统的动力特性及参数分析

3.1 系统的频率特性

首先考察系统振动频率ω1和ωN随参数ξN,k及a2取值的变化曲线,通过绘制ω1-ω0及ωN-ω0曲线(其中ω0为常规换流阀的自振频率),可以了解轨道阻尼、滑块质量及轨道形状对系统振动特征的影响规律。取ξN=0,当a2及k变化时,ω1和ωN的频率曲线如图4所示;取k=0.01,当a2及ξN变化时,ω1和ωN的频率曲线如图5所示。

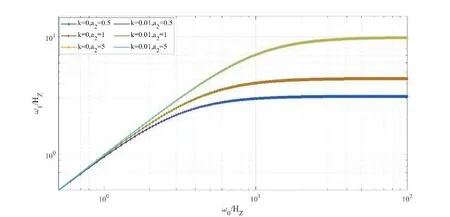
(a) ω1频率曲线

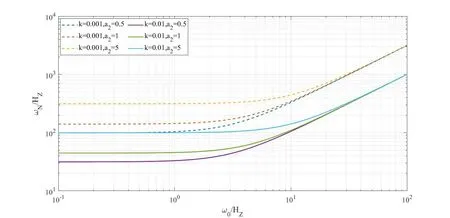
(b) ωN频率曲线

(A) ω1频率曲线

(B) ωN频率曲线

图4、图5结果表明:轨道的形状系数a2的取值可以显著改变换流阀的自振频率,但质量系数k和阻尼比ξN的取值对换流阀的自振频率影响不明显。换流阀在附加滑轨后,改变轨道形状系数a2,不仅可以调节换流阀的自振频率,并且随着换流阀本体的刚度增加,其自振频率将趋于一个只与轨道形状系数a2有关的渐进频率值。

3.2 系统幅频响应曲线

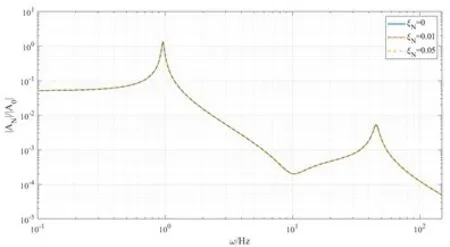
接着考察系统的稳态响应振幅AN和A1随参数ξN,k及a2取值变化对幅频响应曲线的影响。通过绘制|AN|/|A0|-ω及(|AN|+|A1|)/|A0|-ω曲线(其中A0为外激励幅值,ω为激励频率),分析轨道阻尼、滑块质量及轨道形状对系统稳态响应的影响。取ξN=0,k=0.01,当a2变化时,幅频响应曲线如图6所示;取ξN=0,a2=1,当k变化时,幅频响应曲线如图7所示;取k=0.01,a2=1,当ξN变化时,幅频响应曲线如图8所示。

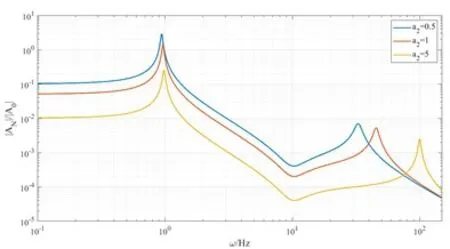
(A) 滑块位移AN幅频响应曲线

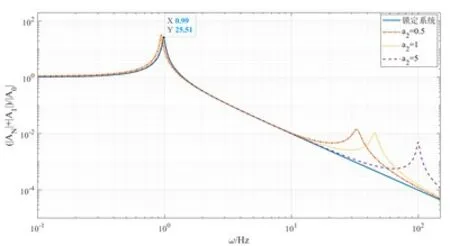
(B) 换流阀绝对位移AN+A1幅频响应曲线

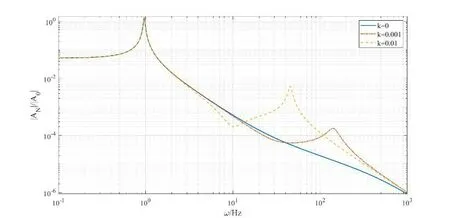
(A) 滑块位移AN幅频响应曲线

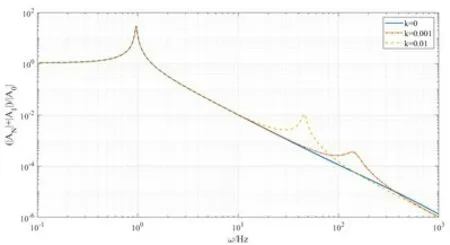
(B) 换流阀绝对位移AN+A1幅频响应曲线

4 结 论

提出一种利用设备悬吊点设置轨道滑动摩擦阻尼实现系统减震的新方法,将悬吊式换流阀结构简化为二自由度动力系统,通过能量原理建立系统的运动方程,给出了运动方程解析解的推导。分析了系统在谐激励下幅频响应曲线的特征,讨论了系统各参数对响应幅值的影响规律,得到如下结论:

(1)调节轨道形状函数系数a2可以同时改变减振系统换流阀和滑块质量子系统的自振频率。

(A) 滑块位移AN幅频响应曲线

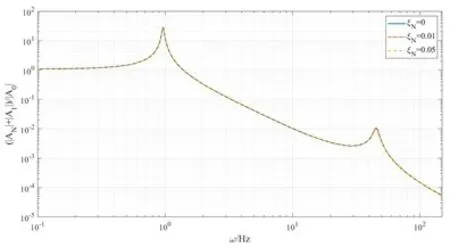
(B) 换流阀绝对位移AN+A1幅频响应曲线

(2)质量系数k和阻尼比ξN的取值对换流阀子系统的自振频率影响不明显。

(3)轨道形状函数系数a2对换流阀和滑块质量子系统的响应幅值均有影响,滑块子系统的振动幅值随a2的减小而显著增大。

(4)轨道滑动系统的阻尼比ξN参数对耦合系统的影响效果存在一个折减因子k/(k+1),其对系统整体耗能能力的影响有所降低。