“一线三直角”全等模型的应用

孙卫华

在平面几何中，有许多基本图形，我们称之为基本模型. 同学们解题时若能发现或构造基本模型，并灵活运用基本模型的有关性质来解决问题，往往会事半功倍.

模型解读

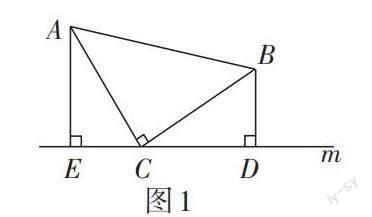
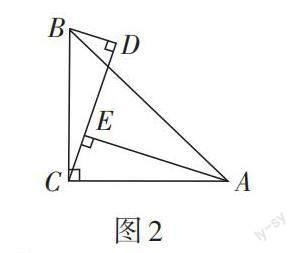
三个直角的顶点落在同一条直线上的图形，被称为“一线三直角”基本模型. 它的常见形式有两种：一是两直角三角形在直线的同侧，如图1（又称“K”字型）；二是两直角三角形在直线的两侧，如图2.

在图1和图2中，∠ACB = ∠AEC = ∠BDC = 90°，若AC = CB（或AE = CD或EC = DB），则△AEC ≌ △CDB.  这两个图形分别在人教版教材第52页和第56页出现过.

在较复杂的图形中，若能寻找或构造出“一线三直角”全等模型，则可迅速找到解决问题的路径.

模型应用

变式1 将模型中的全等三角形的对应线段相等关系转化为线段和差关系.

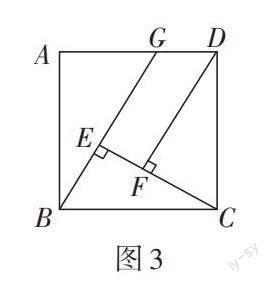
例1 如图3，已知四边形ABCD是正方形，G为线段AD上任意一点，CE⊥BG于点E，DF⊥CE于点F. 求证：DF = BE + EF.

解析：[∵]四边形[ABCD]是正方形，[∴BC=CD]，[∠BCD=90°]，

[∴∠BCE+∠DCF=90°].

[∵]CE[⊥]BG，DF[⊥]CE，[∴∠BEC=∠CFD=90°]，[∴∠BCE+∠CBE=90°]，

[∴∠CBE=∠DCF]，[∴△BCE≌△CDF（AAS）]，[∴BE=CF，CE=DF]，

[∴CE=CF+EF=BE+EF]，[∴DF=BE+EF].

反思：由图2迅速找到图3中“一线三直角”全等模型是解题关键.

变式2 将模型中的全等三角形对应线段相等关系转化为点坐标的确定.

例2 如图4，在△ABC中，∠ACB = 90°，AC = BC，点C的坐标为（-2，0），点A的坐标为（-6，3），则点B的坐标是___________.

解析：过点A，B分别作AD⊥x轴于点D，BE⊥x轴于点E，则∠ADC = ∠ACB = ∠BEC = 90°. 由基本模型图1可知图4中△ADC≌△CEB，所以AD = CE，CD = BE. 又因為点C（-2，0），点A（-6，3），所以AD = 3，CD = 6 - 2 = 4，所以BE = 4，CE = 3，所以OE = 3 - 2 = 1，所以B的坐标为（1，4）. 故应填（1，4）.

反思：受基本模型图1的启发，添加辅助线，找到图4中“一线三直角”全等模型是解题的关键.

变式3 将三个直角的顶点落在同一条直线上，并将部分直角隐去.

例3 如图5，在四边形ABCD中，∠B = 90°，AD[?]BC，△CDC′是等腰直角三角形，∠CDC′= 90°. 若AD = 2，△ADC′的面积等于3，求BC的长.

解析：尽管图5中看上去没有“一线三直角”模型，但受图1的启发，过点D作EF⊥BC于点E，过点C′作C′F⊥EF于点F，就出现了“一线三直角”模型，由上述模型可知△CDE≌△DC'F，所以CE = DF. 又因为AD = 2，△ADC′的面积等于3，所以DF = 3，所以CE = DF = 3，所以BC = BE + CE = 2 + 3 = 5.

反思：这里没有“一线三直角”模型的影子，但受基本模型的启发，可以“无中生有”地创新使用模型.

分层作业

难度系数：★★★解题时间：10分钟

如图6①所示，已知A，B为直线l上两点，点C为直线l上方一动点，连接AC，BC，分别以AC，BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作DD1⊥l于点D1，过点E作EE1⊥l于点E1. （1）如图6②，当点E恰好在直线l上时（此时E1与E重合），试说明DD1 = AB；（2）在图6①中，当D，E两点都在直线l的上方时，试探求三条线段DD1，EE1，AB之间的数量关系，并说明理由；（3）如图6③，当点E在直线l的下方时，请写出三条线段DD1，EE1，AB之间的数量关系，并说明你的理由. （答案见第37页）

（作者单位：江苏省泰州市姜堰区城西实验学校）