基于近红外光谱技术建立木材产地鉴别模型

骆 立, 王静仪, 徐兆军, 那 斌

南京林业大学材料科学与工程学院, 江苏 南京 210037

引 言

我国地域辽阔, 跨温寒带、 温带、 亚热带, 地形复杂, 环境差异大, 树木种类繁多且区系成分复杂, 即使是同一树种的木材, 其理化性质也会因生长条件不同而产生差异, 为达到“适材适用”的目的和确保木制品质量的一致性, 需要快速准确地识别木材产地。 《濒危野生动植物国际贸易公约》指出, 为打击非法砍伐、 保护濒危树种, 需要建立木材追溯系统以追踪木材的地理来源。 因此对于木材及其木制品亟需一种原产地的快速精准识别方法, 而近红外光谱技术是一种简易、 快速、 无损的检测技术, 与机器学习算法相结合被广泛应用于农业、 制药、 环境、 石油化工和生命科学等多个领域。 近年来, 许多学者采用近红外光谱技术结合机器学习对食物(水果、 肉类、 食用油等)[1]、 农作物(玉米、 核桃、 小麦等)[2]和中药材(葛根、 黄柏、 毛地黄等)[3]的地理来源进行识别, 而在木材工业中多用于木材树种识别、 木材分级、 质量评估和缺陷检测等, 关于木材产地鉴别的研究鲜见报道。

近红外光谱是光吸收和光散射两个主要信号的叠加。 光散射是与光从表面反射现象相关的物理信息, 受到微观结构、 表面粗糙度、 内部反射和衍射等影响, 可能与分子的空间分布有关, 但与其化学成分没有直接关系。 然而, 光吸收与聚合物基质中官能团的分子振动有关, 只有具有偶极矩的分子才能被激发到特定的振动模式从而吸收特定波段的红外辐射, 在近红外光谱范围内的光吸收是在中红外光谱范围内发生的基本振动的组合和高阶谐波的结果。 特别是木材作为一种生物质材料, 其具有的吸湿性、 各向异性是影响光谱质量的关键因素。 此外木材样本状态及测试环境也会影响光谱, 使得近红外光谱比其他光谱区域更为复杂且更难以解释[4], 因此必须依赖于校准方法和模型开发[5]。 近红外光谱主要包含C—H、 O—H和N—H三种化学键产生的吸收带, 采集木材的近红外光谱, 由于不同基团产生的光谱吸收峰位置和强度均不同, 吸收光谱也会随着样品成分组成变化而变化, 可结合机器学习算法对木材进行定量分析和定性分析[6]。 机器学习(machine learning, ML)是一门通过编程让计算机从数据中进行学习的科学, 按照不同的分类标准可以分为监督学习和无监督学习, 在线学习和批量学习, 基于实例学习和基于模型学习。 随着数据规模和计算资源的快速增长, 机器学习在理论和实践两方面都取得了重要进展, 为多学科交叉的林业技术领域的数据密集型科学创造了新的机遇[7-8], 为木材质量追溯系统的构建及制约非法木材贸易提供了新的思路和方法。

采用近红外光谱技术对木材进行定性分析主要有树种分类和产地鉴别两个方面。 目前, 已有大量研究证实了近红外光谱技术结合机器学习算法在木材树种分类中存在的巨大潜能[9]。 然而, 木材产地的鉴别模型却多采用传统的化学计量学方法, 例如Prades等[10]基于近红外光谱建立PLS(partial least squares, PLS)模型识别针叶材木塞的产地来源, 验证了近红外光谱技术用于鉴别木材产地的潜力, Yang等[11]研究了近红外光谱对不同树种和不同产地木材样品的鉴别能力, 采用PLS-DA(partial least squares discriminant analysis, PLS-DA)模型, 结果表明近红外光谱技术可以准确地识别木材树种, 但产地的识别精度有待提高。

本工作以近红外光谱技术和机器学习结合为主要技术路线, 探究其在木材地理来源检测领域的可行性, 分别从非线性算法、 回归算法、 分类算法、 概率算法、 集成算法和深度学习算法六个角度选取了支持向量机、 逻辑回归、 K最近邻、 朴素贝叶斯、 随机森林和人工神经网络算法来建立木材产地鉴别模型, 并分别基于主成分分析法(principal component analysis, PCA)与线性判别分析法(linear discriminant analysis, LDA)进行降维处理, 对模型输入降维后的特征矩阵再输出木材产地类别, 并采用学习曲线、 网格搜索法、 K折交叉验证等算法优化模型参数, 最后从模型的准确率与运行时间两个层面评估模型效果。

1 实验部分

1.1 样本制备

以来自两种产地的樟子松、 泡桐、 榉木、 柚木、 椴木和臭椿木块为研究对象, 木块尺寸均为4 cm×4 cm×2 cm(长×宽×高), 每个树种均备有200个木块, 其中每个产地100个木块, 共计1 200个试验样本, 样本树种及产地如表1所示。 为避免木材表面锯痕与老化的影响, 采用100目(粒径150 μm)砂纸对木块进行打磨[12], 并存放在温度为(20±2) ℃、 相对湿度为60%±2%的受控环境中。

表1 样本树种及来源

1.2 光谱采集

近红外光谱的采集系统主要由光谱仪(台湾五铃光学公司, 型号: NIRez)、 计算机(独立显卡, CPU型号: i5)、 光源盒、 光纤探头、 暗箱等构建而成。 为避免室温、 光线等环境变化对实验造成影响, 在暗箱内进行采集作业, 为最大限度地减少木材各向异性对光谱的影响, 每个样本随机采集3个点的光谱数据, 并求其均值作为该样本的光谱数据, 不考虑径切面与弦切面的区别[13]。 将待测样本放置在支架平台上, 光纤探头距待测样本表面约5 mm, 每采集20个样本采用标准聚四氟乙烯白板进行校正。 利用光谱仪配套软件SpectraSmart(台湾五铃光学公司, 版本号: 2018)采集数据, 采样的参数设置为: 光谱范围900～1 650 nm, 光谱分辨率10 nm, 积分时间1 ms, 扫描平均次数500次, 平滑度为5, 同时启用Savitzky-Golay滤波器、 电子暗噪声校正和杂散光校正。 获取光谱数据集后需将其划分为训练集和测试集, 划分前对数据进行乱序处理, 随机抽取30%作为测试集, 70%作为训练集。

1.3 特征工程

在基于机器学习算法建立模型之前需要对光谱数据进行清洗和组织, 这个环节称为特征工程, 即从原始数据中提取特征并将其转换为适合机器学习模型的模式, 从而提高机器学习的性能。 采集得到的木材光谱数据具有112个特征, 属于高维数据。 高维特征会含有冗余数据, 这将不利于分类模型的构建, 因此需要对高维特征向量进行降维处理。 PCA是一种无监督学习的降维技术, 即在保留数据重要信息的同时消除那些“无信息量的信息”。 PCA关注的是线性相关性, 试图将数据挤压到一个维度大小小于原空间的线性子空间从而消除这些“臃肿”, 其核心思想是使用一些新特征代替冗余特征, 这些新特征能恰当地总结初始特征控件中包含的信息。 除了去除高维光谱数据中的重叠信号, PCA还常常将数据降维到2维或3维以可视化数据, 有利于了解和探索数据集。 与PCA不同, LDA是有监督学习的降维技术, 即每个样本是有类别输出的。 其核心思想是“投影后类内方差最小, 类间方差最大”, 即将数据投影在低维度上, 并且投影后同种类别数据的投影点尽可能接近, 不同类别数据的投影中心点尽可能远, 局限性是最多只能降到类别数减1的维度。

1.4 模型建立

支持向量机[14]是一种基于统计学习理论的非线性机器学习方法, 其基本思想是通过非线性变换将输入空间变换到一个高维的特征空间, 并在新空间中寻找最优的线性分界面, 在处理小样本、 高维特征和非线性等数据集上具有优异的表现。

逻辑回归是一种常用的分类算法, 也是一种因变量为离散值的回归模型。 在木材产地识别的决策问题中, 逻辑回归基于木材的高维光谱特征值来估计木材产地类别的概率, 模型本身并不是一个分类器, 而是选择一个阈值, 将概率大于此阈值的输入视为一类, 小于此阈值的视为另一类。

K最近邻算法通过测量不同特征之间的欧几里德距离或曼哈顿距离来进行分类[15], 其分类的核心思想是在样本特征空间中选择K个相邻的样本, 如果K个相邻的样本大多数属于某一类, 则该测试样本也属于这个类。

朴素贝叶斯是一种直接衡量标签和特征之间的概率关系的有监督学习算法, 是一种专注分类的算法, 采用了“特征条件独立”的假设, 假设已知类别的情况下所有特征相互独立。

随机森林[16]是非常具有代表性的Bagging集成算法, 其基评估器均为决策树, 在树的生长上引入了更多的随机性, 分裂节点时不再是搜索最好的特征, 而是在一个随机生成的特征子集里搜索最好的特征, 从而生成一个整体性能更优的模型。

人工神经网络是一种可用于处理具有多个节点和多个输出点实际问题的网络结构[17], 其为深度学习的核心, 功能强大且可扩展, 非常适合处理大型和高度复杂的机器学习任务。 人工神经网络领域中的多层感知器(multilayer perceptron, MLP), 由一层输入层、 一层或多层隐藏层和一层输出层组成, 信号仅从输入到输出流动, 又称多层前馈神经网络。

公元前481年，田常在民众的支持下，打败了齐国当权贵族监止，并杀死了齐国奴隶主贵族的最高代表齐简公。从此，以田氏为首的齐国地主阶级势力反对奴隶主旧有阶级的斗争，取得了决定性的胜利。据《史记·田敬仲世家》记载，在田常杀死齐简公以后的五年，即公元前476年，“齐国之政，皆归田常”，由奴隶主贵族统治的姜齐政杖已名存实亡，中国历史上第一个封建地主政权——田齐政权建立起来了。

2 结果与讨论

2.1 光谱数据分析

木材的原始近红外高维光谱包含大量冗余信息、 特征峰高度混叠、 信噪比较低, 为探索和深入了解数据的分布情况, 采用PCA降维技术将高维空间降至2维, 并以第一主成分为横坐标、 第二主成分为纵坐标可视化光谱数据, 如图1。 由图1可知, 榉木不同产地的光谱数据之间区分界限十分明晰, 樟子松、 泡桐、 柚木不同产地的光谱数据呈现出较高的聚合度但边界线处数据点重叠混淆, 而臭椿和椴木两个产地的光谱数据重叠度较高。 由此可得, 榉木的产地鉴别模型易于建立, 而臭椿和椴木的建模难度较大。

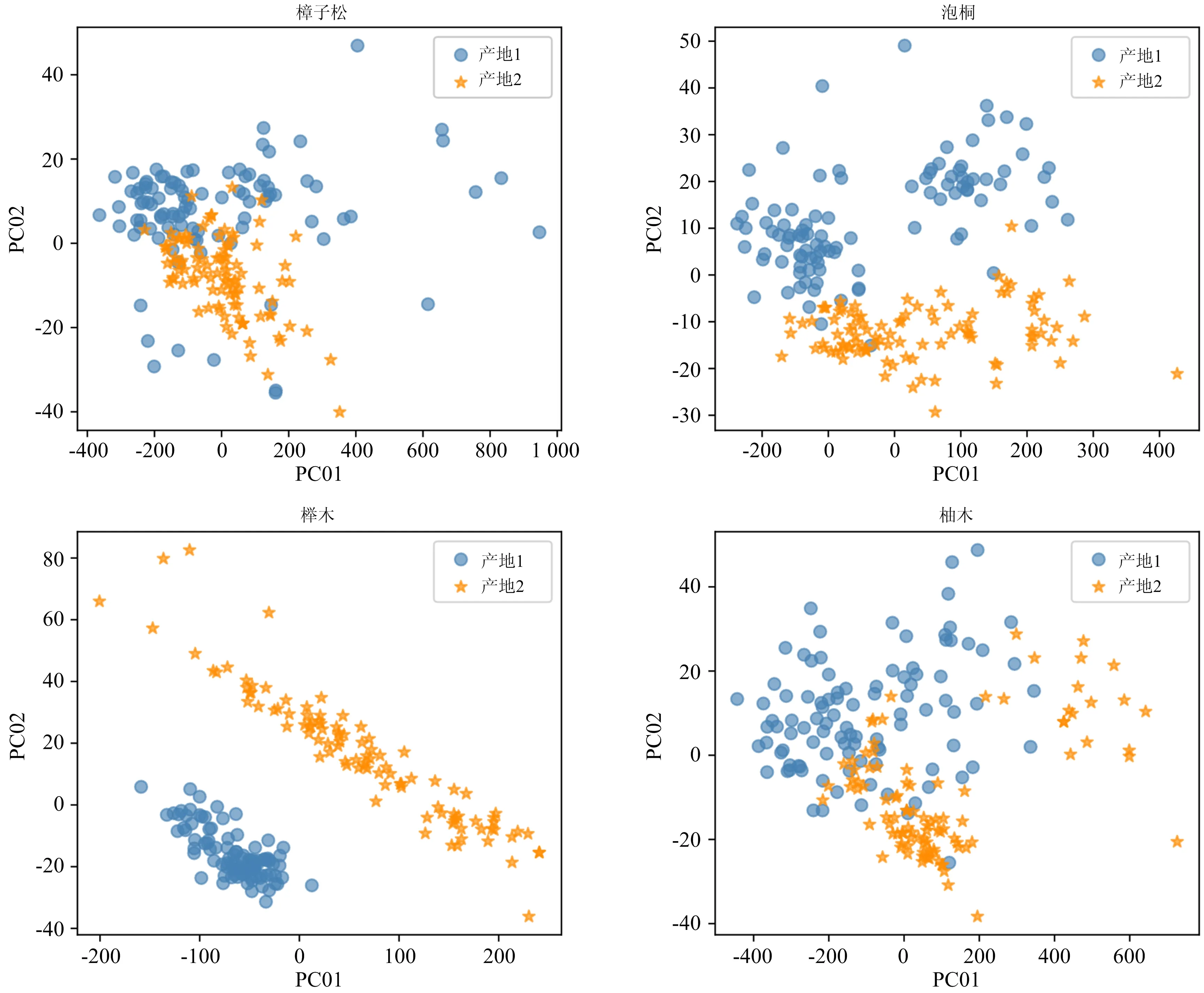
图1 6种木材的前2个主成分散点图

2.2 数据降维

基于对光谱数据集的分析, 分别采用无监督的PCA和有监督的LDA对木材原始光谱进行降维处理。 降维算法最重要的参数是降维后保留的特征维度, 由于只有两个树种标签, LDA只能将维度降到1维, 而PCA需要通过学习曲线来确定特征维度。 对于PCA降维技术, 训练集的前5个主成分累计贡献率见表2, 6个树种的前5个主成分累计贡献率均达到了99.99%, 表明在滤掉噪声的同时携带了原始数据足够的信息。 为对比降维前后的数据差异, 分别将未降维的原始数据、 PCA降维后的数据和LDA降维后的数据作为模型输入导入支持向量机模型中, 模型的各项参数均为默认值(kernel=“rbf”、 gamma=“scale”), 不同输入得到的准确率如表3。 由表3可知, 经过降维处理, 模型的准确率得到了显著地提升, 其中LDA的效果优于PCA。

表2 训练集的主成分累计贡献率(%)

表3 不同模型输入的模型准确率(%)

2.3 模型优化

模型的超参数是模型外部的配置, 对模型效果具有至关重要的作用, 通常需要使用者自行定义, 为了提高模型的泛化能力, 采用学习曲线、 网格搜索法、 K折交叉验证等算法对模型的超参数进行选取和优化, 表4为不同模型的参数设置。

表4 不同模型的参数设置

支持向量机模型实现的关键是核函数kernel的选取[18], 支持向量机常用的核函数有线性内核、 多项式内核、 双曲正切内核和高斯径向内核, 在此选择效果最佳的高斯径向内核(Radial Basis Function, RBF), 即kernel=“rbf”。 此外, 还需自定义惩罚因子C和RBF核函数宽度gamma这两个超参数, 采用网格搜索法结合5折交叉验证来获取C与gamma的最佳组合, 即C=20、 gamma=0.038 9。

正则化是用于防止模型过拟合的过程, 逻辑回归常用的有L1-范数正则化和L2-范数正则化, 分别通过在损失函数后加上参数向量θ的L1范式和L2范式的倍数来实现。 L1-范数正则化和L2-范数正则化都能控制模型的过拟合, 但作用效果并不相同, 当正则化的强度增大, L1-范数正则化正则化会使参数θ压缩为0, 其本质是一个特征选择的过程, L2-范数正则化只会让携带信息少, 对模型贡献不大的特征参数接近于0。 由于在特征工程中已进行降维处理, 数据维度不高, 正则化的主要目的是防止过拟合, 选择L2即可。

K最近邻算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别, 则该样本也属于这个类别, 并具有这个类别上样本的特性, K最近邻近算法的K值通过n_neighbors参数来调节, 通过学习曲线得到n_neighbors=1。

在实例化模型时, 不需要对高斯朴素贝叶斯类输入任何的参数, 模型易于建立, 但没有参数以供调整, 意味着贝叶斯算法的成长空间不大, 若是效果不理想, 一般考虑替换效果更佳的模型。

在分类问题中, 随机森林的基评估器决策树视为分类树, 基评估器的数量n_estimators是随机森林分类器最重要的参数。 n_estimators越大, 模型往往越好, 但当n_estimators接近决策边界后, 模型的精确性便不会发生大的波动, 且n_estimators越大, 所需的计算量与内存也相应地增加。 因此, 需要在训练难度与模型效果之间寻求平衡点, 通过学习曲线获取最佳的n_estimators为80。 随机森林的本质是一种袋装集成算法, 是对每棵分类树的预测结果进行平均或用多数表决原则来决定集成评估器的结果, 采用参数random_state可以控制生成森林的模式。 当random_state固定时, 随机森林生成是一组固定的树, 但是每棵分类树均具有“随机挑选特征进行分枝”的随机性, 当这种随机性越大时, 袋装法的效果就越好。 基于本光谱数据集, 选取random_state=0。

2.4 模型结果及评价

按照表4的参数对每个树种建立相同的模型, 各个模型对木材产地鉴别的准确率见表5。 由表5可知, 樟子松、 泡桐、 榉木、 柚木、 椴木和臭椿产地鉴别的最高准确率分别为98.3%、 100%、 100%、 100%、 100%、 98.3%, 值得注意的是, 大多数基于LDA的分类模型效果要优于基于PCA的分类模型。 其中, 泡桐、 榉木和柚木两种产地的区分度较高, 在PCA或LDA的降维处理下, 6种模型均能达到100%的识别率。 此外, 对于樟子松产地的鉴别, 6种模型的准确率也均能达到98.3%。 但对于椴木与臭椿而言, 6种模型的准确率差异较大, 分别在65%～100%和76%～98.3%之间波动。

表5 六个树种不同模型的准确率(%)

在机器学习算法领域, 追求的主要包括算法效果与运算速度两个方面。 对于樟子松、 泡桐、 榉木、 柚木4个树种的产地鉴别, 6种机器学习算法均能达到相同的准确率, 因此, 需要对比分析6种模型的运行时间, 6个树种不同模型的运行时间见表6。 由表6可知, 基于SVM、 LR、 KNN和NB建立的木材产地鉴别模型运行时间相差较小, 运行时间最长的是ANN, 远远超过于其余算法, RF次之。 因此, 对于这4个树种而言, ANN和RF的运行时间过长, 不是最佳的模型选择。

表6 六个树种不同模型的运行时间(s)

而对于椴木与臭椿, 各个模型效果差别较大, 评价模型时需要平衡模型的精度与速度。 但首先追求的是模型的高准确率, 椴木产地识别率最高的前两个模型是LDA-NB模型与PCA-ANN模型, 分别达到95%和100%, 臭椿产地识别率最高的前两个模型是PCA-KNN和PCA-ANN模型, 分别达到96.7%和98.3%。 为进一步探索模型的运行时间, 绘制椴木和臭椿在不同训练样本量下的拟合时间曲线, 由图2可以发现, PCA-ANN的运行时间是LDA-NB和PCA-KNN的几十倍, 且拟合时间随着训练样本量的不同而产生较大的波动, 这是由于十分复杂的人工神经网络为追求算法效果的极致而几乎放弃了运算速度。

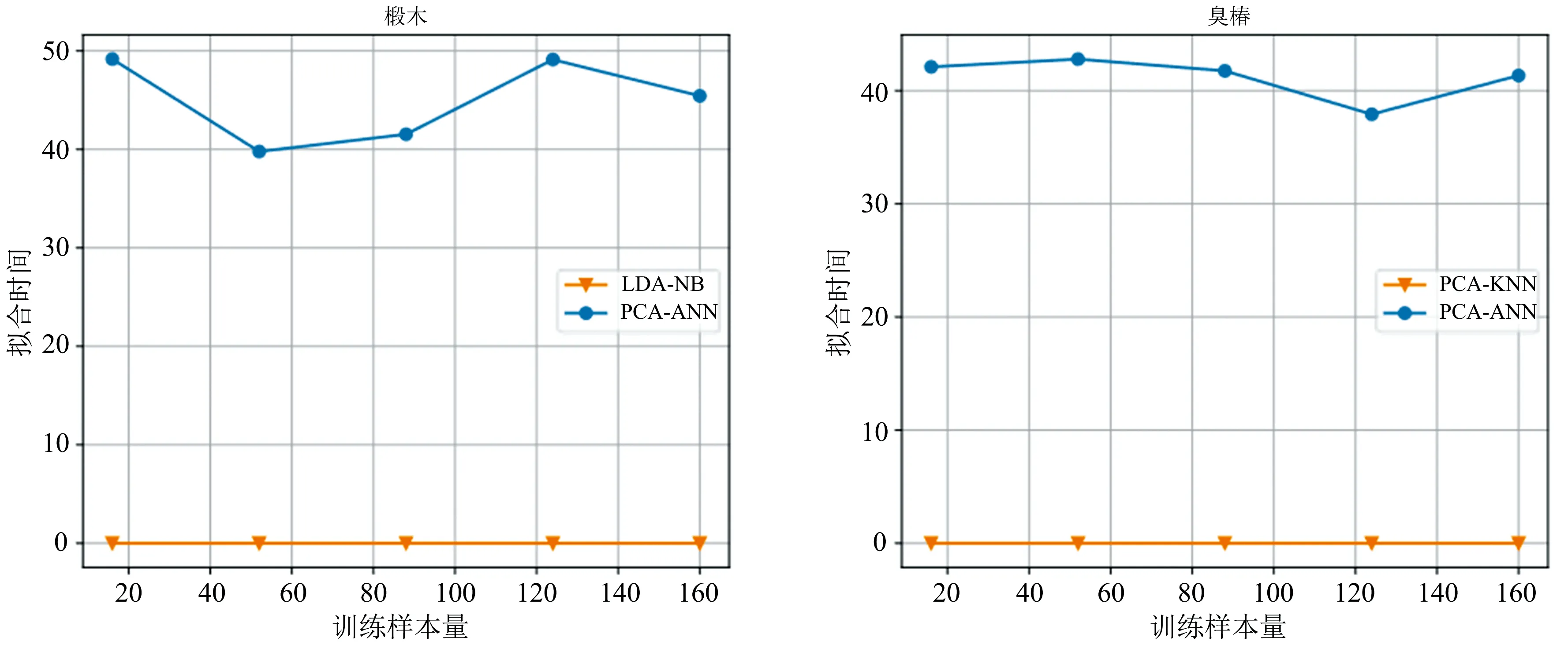
图2 椴木与臭椿不同训练样本量下的拟合时间

图3为4种模型的混淆矩阵, 椴木与臭椿准确率最高的两种分类器差距较小, 因此需要进一步评估模型的精度。 混淆矩阵是二分类问题的多维衡量指标体系, 在该体系中可以获取真正、 真负、 假正和假负四种分类结果。 由图3可知, 臭椿的两种模型能正确识别所有产地2的木材, 而对于产地1, PCA-KNN误判了2个样本, PCA-ANN误判了1个样本, 结合两种模型的运行速率, 综合考虑认为臭椿的PCA-KNN模型优于PCA-ANN模型。 椴木两种模型产地1的识别率均能达到100%, 而当PCA-ANN对产地2的木材全部正确识别时LDA-NB误识了3个样本。

图3 四种模型的混淆矩阵

3 结 论

基于近红外光谱技术, 采用6种机器算法构建校准模型, 以期对木材的地理来源进行识别, 主要从精度和速度两个层面评估模型, 主要结论如下:

(1)基于近红外光谱技术结合机器学习能有效地识别木材产地, 6种模型均能正确分类。 整体而言, 基于LDA降维的模型效果优于基于PCA降维的模型效果, 非线性模型的效果优于线性模型的效果。

(2)对于相同的数据集, SVM、 LR、 KNN和NB的运行时间较短且相差较小, 其次是RF。 对比其余算法, 人工神经网络在各个数据集上均具有优异的精度, 但是在运行时长上不具备竞争力。

(3)为基于近红外光谱技术结合机器学习识别木材产地提供了一定的理论依据, 但未来需要代表性更广泛的大型数据来构建更稳健的模型以检测更多的地理来源。