基于X射线吸收光谱法的塑料薄膜厚度测量

方 正, 王涵博

厦门大学仪器与电气系, 福建 厦门 361102

引 言

近些年来, 我国塑料薄膜的生产量占到了国内塑料制品总生产量的五分之一, 属于增长速度非常可观的塑料制品。 据分析, 中国的塑料薄膜产业正处于蓬勃发展的大好时期, 未来的需求量还将以超过年均9%的比例飞速增长。 在如此巨大的塑料薄膜产品需求之下, 严格把关塑料薄膜的生产质量至关重要[1-2]。 在塑料薄膜质量检测的流水线上, 塑料薄膜的厚度是一项关键指标, 影响着塑料薄膜在后续使用到包装过程中的力学强度性能, 其均匀性是保证塑料薄膜产品具备特定保护功能的重要条件。

首先, 厚度均匀性影响着薄膜张力的控制, 例如塑料薄膜包装印刷技术中最常见的凹版印刷塑料薄膜, 若厚度均匀性控制不准确, 就非常容易出现印刷故障; 其次, 若将厚度不均匀的薄膜材料继续用于产品外包装, 在使用过程中, 也易出现机械性能薄弱点, 如果在运输或储存的过程中外包装不慎受到外力冲击, 这些机械性能薄弱点就较容易出现裂痕、 孔洞等, 从而使塑料薄膜的保护功能降低甚至直接丧失。 除此之外, 有的塑料薄膜制品需要薄膜具备独特的光学和电学性质, 这同样需要薄膜厚度达到相当精确的标准, 以符合薄膜材料的光学、 电学性质研究需要[3-4]。

因此, 对塑料薄膜的厚度进行有效地控制, 既能提高塑料制品的质量, 还能降低材料的损耗, 提高生产效率。 塑料薄膜厚度检测作为薄膜制造行业的一项基础的检测项目, 需要精确测量塑料薄膜的厚度, 严格控制薄膜厚度的均匀性, 保证薄膜具备特殊性能指标[5]。

1 测厚技术

在外包装材料厚度检测的方法中, 离线测厚技术最先用于塑料薄膜厚度的测量。 但伴随着射线技术日趋成熟完善, 在线测厚模式迅速兴起, 它能够在较短时间内得到厚度信息, 在生产线上及时反映到控制端, 快速调整相关参数, 从而保障生产质量。 离线测厚与在线测厚均已有广泛的应用, 常用的方法如下:

1.1 β射线技术

β射线技术是厚度测量中运用最早的射线类技术, 始于20世纪60年代, 原理是β射线通过物质时强度减弱, 具备精度高、 速度快的优势。 该技术可用于检测10～100 μm的薄膜, 测厚精度为0.1 μm[6-8]。

1.2 红外光谱技术

2012年徐源等通过对塑料薄膜红外光谱的研究, 利用红外吸收光谱能够显示物质的化学组成和分子结构信息的特点, 结合朗伯-比尔定律得出特征峰的吸光率与薄膜厚度之间的工作曲线, 拟合相关度达到99.497%, 验证了红外光谱法测厚的可行性[9-11]。

1.3 X射线荧光技术

2012年李军通过反散射法标定塑料薄膜厚度的实验, 发现厚度在10～800 μm范围内的聚乙烯塑料膜, 其厚度值与反散射荧光强度存在正相关的联系, 通过标定可实现薄膜测厚, 测量精度能够达到3 μm。 但一次测厚需200 s, 检测速度有待提高[12]。

1.4 X射线衍射法

2018年陈涌得进行了X射线衍射法测厚的实验, 该技术利用了相同材料塑料薄膜叠加后的空间域周期性结构, 通过分析衍射峰的数据测量膜厚。 在精密装调样品台并在拟合期间选择合适的衍射峰后, 薄膜厚度的误差能够控制在0.01 nm以下[13]。

1.5 超声波测厚仪

超声波测厚仪设备体积小、 便于携带, 其测厚原理利用的是超声波的反射, 能够测量各种超声波良导体材料的厚度, 例如金属、 塑料、 陶瓷、 玻璃。 此类设备操作繁琐, 需要使用耦合剂排除探头与被测物体间的空气, 使超声波能有效的进入被测物体内部[14-16]。

1.6 机械测厚仪

机械测厚仪通过在测量厚度之前对待测试样的表面施加一定压力, 保证探头和被测面无间隙, 可得到稳定性好的数据, 应用领域广泛。 其测量精度取决于位置反馈传感器的精度。 除此之外, 机械测厚仪对振动敏感, 会因此导致测量误差, 因此为保证设备自身的稳定性并屏蔽外界环境的干扰, 机械测厚仪通常厚重庞大, 不方便搬运, 只能在室内使用[17-19]。

目前市面上的塑料薄膜厚度测量手段已是相当丰富, 但是对于使用X射线吸收光谱法的原理进行厚度测量却鲜有报道。 相较其他射线类技术, X射线吸收光谱法的优势在于穿透力更强[20], 能够反映特定能量穿透不同样本时的具体光谱数据[21], 能够观测到更多的细节信息, 这在某种程度上能够提高厚度测量的精度。 本实验正是出于这样的考虑, 初步尝试运用X射线吸收光谱法的原理测量塑料薄膜的厚度, 同时, 使用机器学习算法分析光谱数据, 并与传统的光子数量测厚相比较, 对该方法的实际可行性作一定分析。

2 实验部分

2.1 实验环境

实验器材为完整的X射线光谱检测系统[22], 由本实验室自主搭建, 图1为基本框架。 光谱检测系统的关键组成部分包括X射线管、 X射线探测器以及高压电源。 核心部件的主要性能指标(表1)。

表1 核心部件的型号与性能

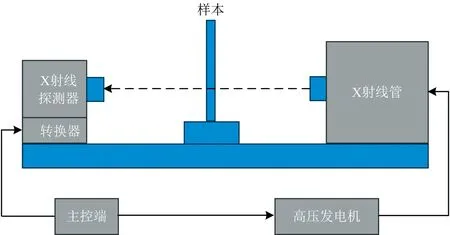
图1 X射线光谱检测系统

在本次试验中, 为得到较为理想的X射线吸收光谱数据, 进行了数次实验环境参数的调试。 最终, 得到较理想的实验环境参数设置(表2)。 实验材料采用塑料薄膜中最为常见的PE膜, 即聚乙烯塑料膜, 由深圳西半球有限公司生产, 其标定的参数为20 μm的单层膜厚以及4 cm的膜宽。

表2 实验环境参数

2.2 样本制备

制作不同厚度的塑料薄膜样本, 采用多层塑料薄膜缠绕叠加的方法。 具体过程如下: 将塑料薄膜逐层缠绕在特制带孔模具上, 以每5层膜即100 μm为分度值, 制作100、 200、 300、 400、 500、 600、 700、 800、 900、 1 000 μm的样本, 即依次缠绕5、 10、 15、 20、 25、 30、 35、 40、 45、 50层, 一共10组。 缠绕过程需要避免薄膜的褶皱与过度拉伸, 减小人为操作误差。 如下为具体样本参数(表3)和样本实物图(图2)。

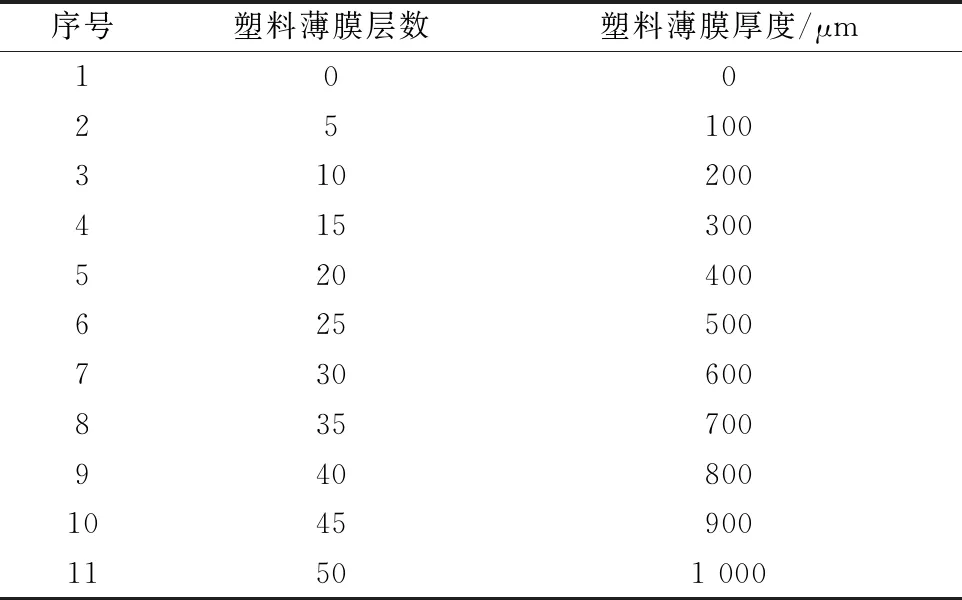
表3 样品参数

图2 缠绕塑料薄膜的待测样本

2.3 数据采集

由于设备本身存在测量误差, 实验需要在同一环境下进行, 并进行多次数据采集。 每组样本进行40次数据采集, 每次采集前需要适当调整X射线穿透样本的部位; 此外, 不放置样本时的空白背景也需要40次数据采集, 用于后续对比分析。 综合测厚的样本与空白背景, 总计得到440组原始光谱数据。 空白背景数据如图3所示, 其横坐标为通道数, 纵坐标为出射光子数, 选取数据明显的140个通道, 通道号为56—195。

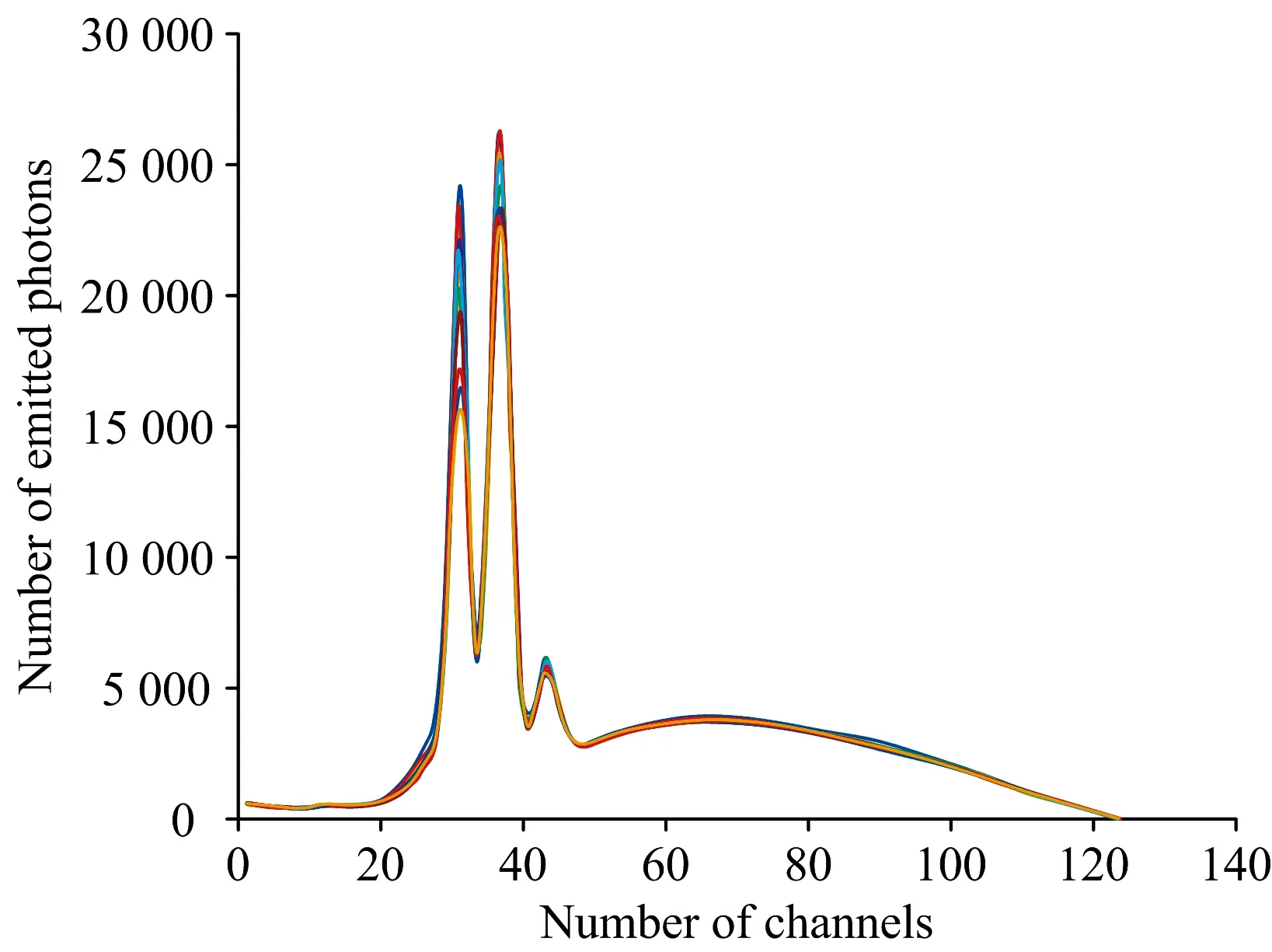
图3 背景光谱图

10种厚度塑料薄膜的原始光谱图如图4所示, 其中横坐标代表入射X射线的能量, 纵坐标为出射光子数, 即出射X射线的强度。 在实际的数据分析过程中, 有必要将通道数转化为X射线光子能量。 X射线探测器的通道数为0到(2n-1), 通道数的选择通常为256道、 512道、 1 024道、 2 048道、 4 096道、 8 192道, 对应的n取8、 9、 10、 11、 12。 X射线光子能量与通道数之间的关系式为

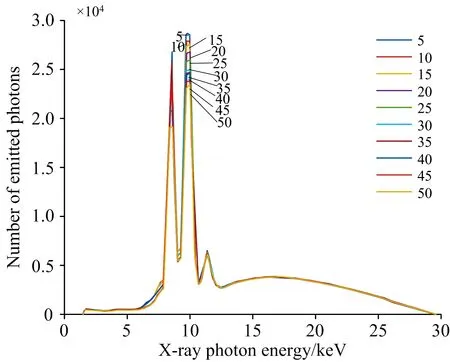
图4 10种样本的原始光谱图

E=2 010(n-0.333 3)

(1)

图4中的三个波峰是由阳极靶材料钨的特性引起的, 属于系统本身的特征波峰, 三个波峰的能量依次为8.538、 9.692和11.308 keV。 10种厚度塑料薄膜的平均值光谱图如图5所示, 其中横坐标为能道数, 纵坐标为出射光子数。

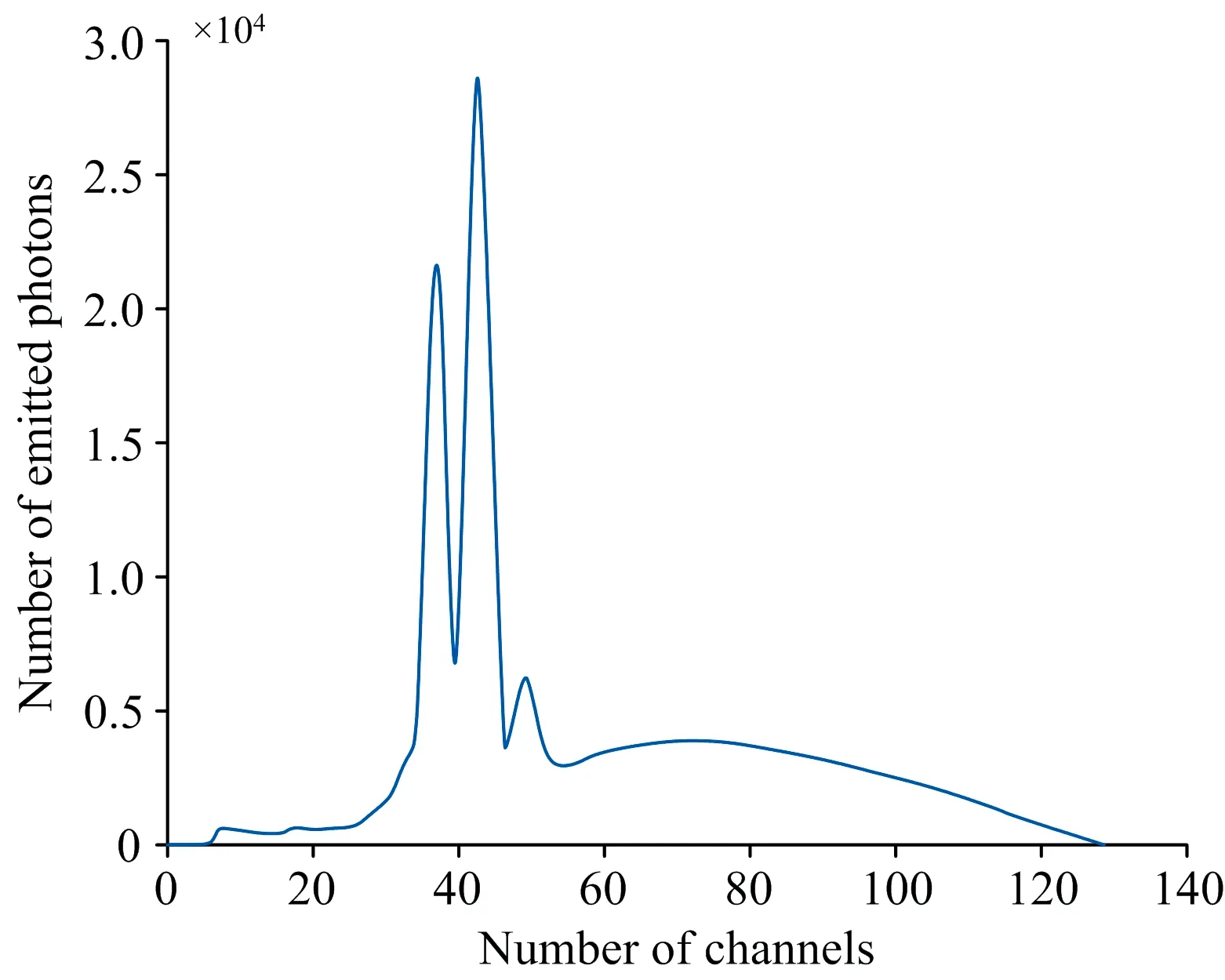
图5 10种厚度塑料薄膜的平均值光谱图

通过出射X射线的能量可以看到不同厚度的样本对X射线的吸收有明显的差别, 在峰值处尤为明显, 而在入射能量过大与过小时区别不大。

3 结果与讨论

3.1 数据降维与特征提取

根据本实验所得数据的类型, 选择主成分分析方法(PCA)做特征提取。 主成分分析是一种用于大量数据的信息筛选、 降维的常用工具[23], 擅于将多维的信息降低到相当有限的维度。 其基本原理是利用原始的n维数据找出若干个相互正交的向量, 其第一个向量是原始数据中方差最大的向量, 第二个向量是在与第一个向量正交的向量中方差最大的, 以此类推得到n个新向量。 而实际上, 只有前几个向量方差较大, 后续向量方差几乎为0, 所以保留方差较大的几个向量即可。

具体的实现过程如下: 假设待降维的数据集为Y={y1,y2,y3, …,yn}, 那么首先需要通过以式(2)构建协方差矩阵X

(2)

再用线性代数特征值分解方法求该协方差矩阵X的特征值和特征向量, 每个特征值的数值即代表一项主成分的占比, 对应的特征向量与原数据集相乘即可得到该方向主成分提取后转化的具体数值。 若将特征值由大到小排列, 选取最大的k个, 其对应特征向量组成矩阵P, 那么特征提取后的数据集Z便可由式(3)得到

Z=PY

(3)

在对测量所得的原始光谱数据进行主成分分析后, 得到如表4所示的主成分贡献率表, 图中只列出了占比前10的主成分分量。

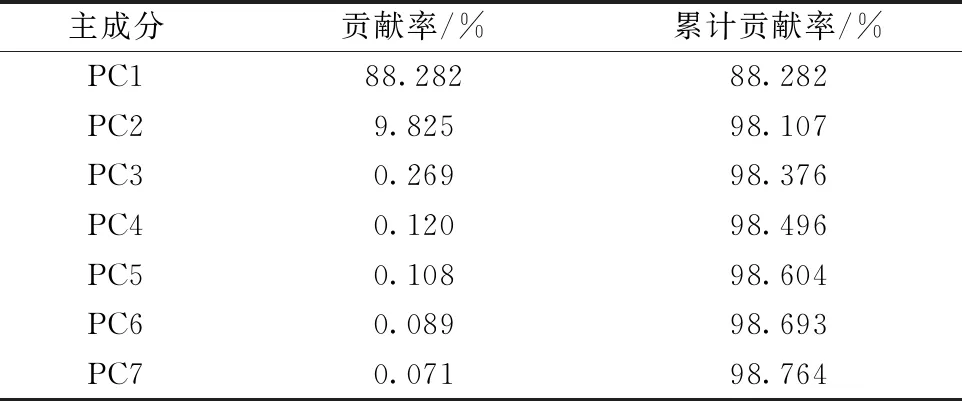
表4 PCA特征提取后主要主成分的贡献率

从表4中可以得到, PC1涵盖了光谱中 88.281 7%的信息, PC2和PC3分别解释9.824 4%和0.269 1%的信息, 光前三项主成分的贡献率相加就已经达到98.375 2%, 基本能够解释光谱数据的全部信息。 可以根据占比最大的前两个特征做出不同厚度下主成分分析的二维图, 如图6所示, 其中横坐标为主成分PC1, 纵坐标为主成分PC2。

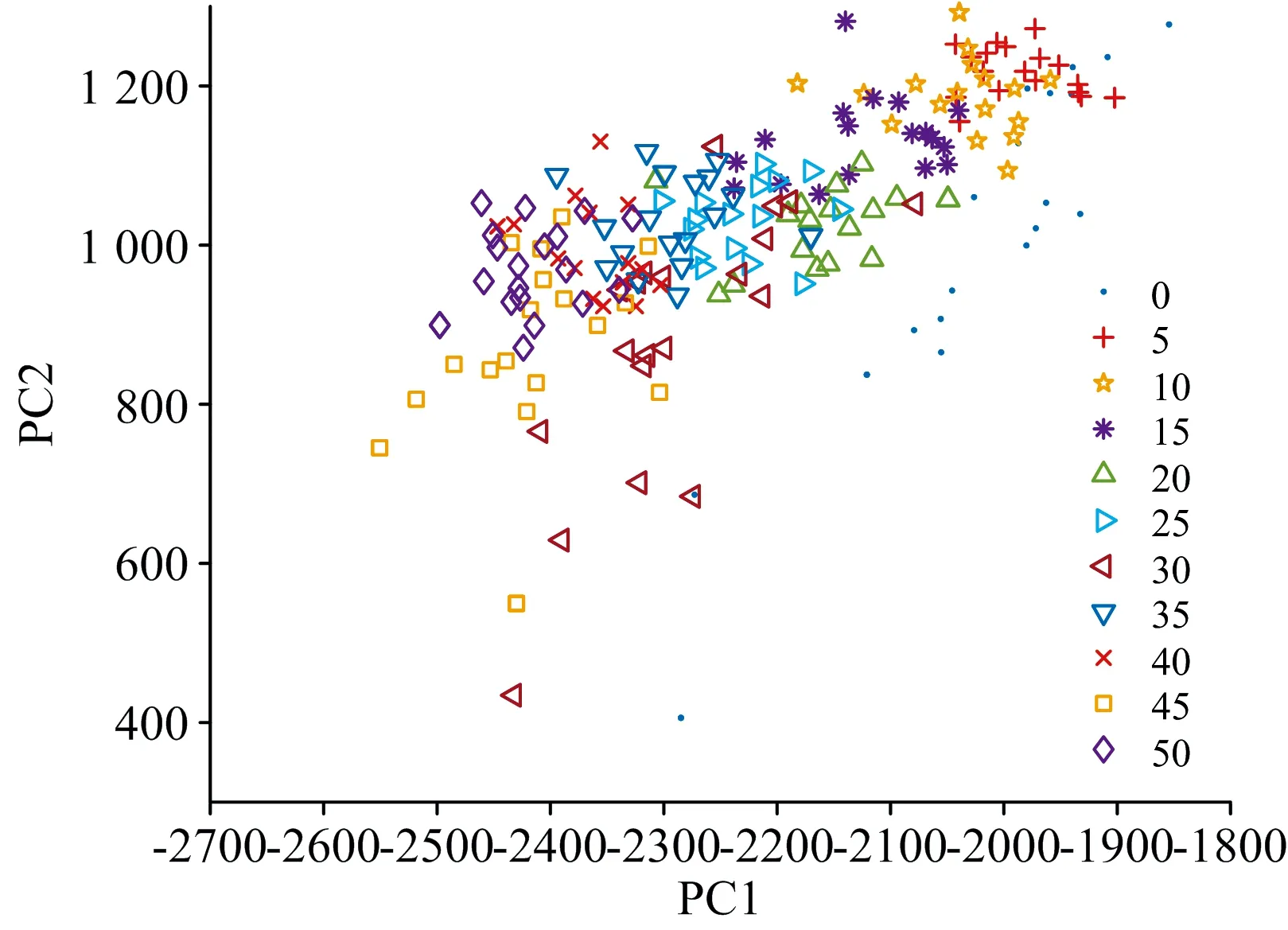
图6 10种厚度主成分分析二维图

由图6可见, 在PCA特征提取后, 对不同厚度的塑料薄膜来说, 它们在PC1的方向上区分较为明显, 在PC2的方向上起伏较大。 由于塑料薄膜厚度极小, 所以在相邻厚度的数据上有一定的重叠, 但是也能基本实现区分。 所以在进行PCA主成分分析后, 还需要通过学习进一步实现分类辨识。

3.2 通过BP神经网络的厚度识别

3.2.1 神经网络的选择

由主成分分析的二维图结果可见, 不同厚度下的数据点存在重叠交错的现象, 一般的线性计算无法实现对各数据点的分类预测, 需要采用非线性拟合计算。 而BP神经网络便是一种成熟的具备非线性映射能力的神经网络模型, 能够拟合出高精度的非线性连续函数。 且BP神经网络拥有较好的自学习能力、 泛化能力和容错能力, 能够实现复杂模型的训练与预测。 而针对BP神经网络收敛速度慢的问题, 会因为主成分分析后的数据降维处理, 大幅度地提高BP神经网络的训练效率, 同时, 主成分分析也有利于提高BP神经网络预测的准确率。 基于以上的优点, 选择BP神经网络作为厚度预测模型。

3.2.2 BP神经网络分类原理

BP神经网络是一种按误差反向传播训练的多层前馈网络, 包括输入层、 隐含层和输出层, 能够在计算单元为非线性函数时依然给出对应的映射关系, 因而其优势在于具备将任意复杂模型进行分类以及多维函数实现映射的能力[24-26]。 BP神经网络的基本过程如下:

首先是顺向过程, 数据由输入层进入, 经过隐含层, 在输出层输出期望值。 输入层一般会用一个线性函数作为激励, 最常用的函数如

(4)

输入层的数据进入隐含层, 在隐含层中建立输入数据与输出数据的映射关系, 隐含层的神经元的输入值为

(5)

式(5)中,Xij表示隐含层中第i层第j个神经元的输入,ni-1表示第(i-1)层神经元的个数,o(i-1)h表示第(i-1)层第i个神经元的输出,ω(i-1)hj表示第(i-1)层第h个神经元与第(i-1)层第j个神经元的权值,b表示神经元的偏置。

最后是输出层, 输出的数据即为网络的预测值; 而输入值的计算与隐含层类似, 等于上一层神经元的输出乘上相应权值的和。

顺向过程后, 需要进行逆向过程, 这才是网络真正的训练, 通过误差来更新网络的权值和偏置值, 逐渐使网络趋于完善。 式(6)为权值的更新公式

ωijk=(t+1)=ωijk(t)+ηδikoij

(6)

式(6)中,η为学习速率,δik为误差。

3.2.3 BP神经网络模型建立

对PCA处理过后的440组数据进行随机筛选, 其中70%用作训练集, 参与神经网络模型训练, 15%作为验证集, 15%作为测试集评估辨识准确率。 进入神经网络输入层的是已经经过 PCA 特征提取后的3个主成分组成的系数矩阵, 隐含层的神经元数量设置为20, 输出层为各组数据对应的塑料薄膜缠绕层数, 与厚度对应关系见表3, 以此建立结构为3-20-11的BP神经网络模型, 拟合结果如图7(a)和(b)所示, 其中横坐标为数据的实际层数, 纵坐标为数据的预测层数。

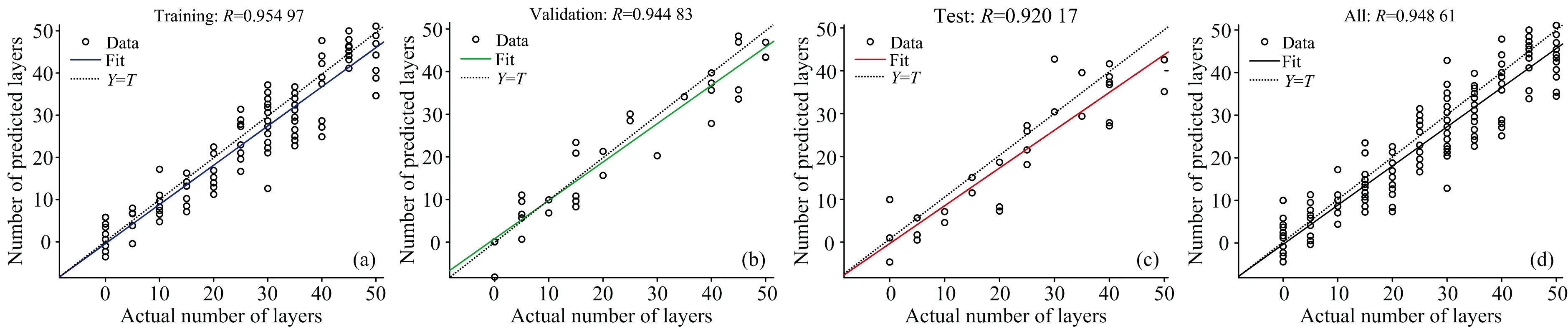
图7 (a)训练集数据拟合度; (b)验证集数据拟合度; (c)测试集数据拟合度; (d)全部数据拟合度

对于回归曲线的评估, 将从拟合优度[27]与 RMSE[28]两方面进行。 拟合优度反映的是回归直线与实际值的拟合程度, 衡量拟合优度的参数是确定系数R2,R2越接近1表示回归直线对实际值的拟合程度越好, 越接近0表示拟合程度越差。R2的具体计算过程如式(7)

(7)

RMSE是指均方根误差, 用于衡量预测值与实际值之间的误差, 具体计算过程如式(8)

(8)

3.3 数据归一化后的BP神经网络训练

3.3.1 原始数据归一化

归一化[29]是一种数据无量纲化处理的常用手段, 能够消除仪器误差, 加快神经网络的运行速度。 采用线性函数归一化的方法将原始数据变换到[0, 1]之间, 其具体过程如式(9)

(9)

式(9)中,Knorm为归一化后的数据,X为原始数据,Xmax为光谱最大值,Xmin为光谱最小值。 原始光谱数据归一化后结果如图8所示。

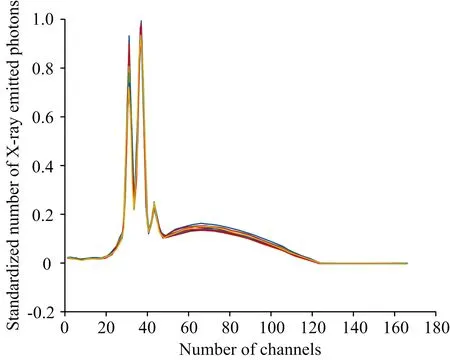
图8 10种厚度归一化后的光谱图

3.3.2 归一化后的BP神经网络训练

将归一化后的440组数据进行主成分分析, 主成分分析结果与不经过归一化处理时相同。 同样选取主成分中占比最大的前三项作为神经网络的输入, 随机筛选其中70%作为训练集, 15%作为验证集, 15%作为测试集训练神经网络模型。 归一化后的神经网络拟合结果如图9(a)和(b)所示, 其中横坐标为数据的实际层数, 纵坐标为数据的预测层数。 在原始数据进行归一化处理后, 测试集的R2=0.984, RSME=2.50, 与未进行归一化的训练模型相比, 回归曲线的拟合程度更高, 预测值与实际值的误差在2.5层膜, 即50 μm, 也比未归一化时更精确。

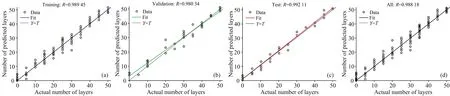
图9 (a)归一化后训练集拟合度; (b)归一化后验证集拟合度; (c)归一化后测试集拟合度; (d)归一化后全部数据拟合度

3.4 基于光子总数的BP神经网络训练

将原始数据中每一组数据的512个数据点求和, 得到每组数据的光子总数, 以此作为神经网络的输入, 对应的塑料薄膜层数作为神经网络的输出, 随机筛选其中70%作为训练集, 15%作为验证集, 15%作为测试集训练神经网络模型。 基于光子总数的神经网络拟合结果如图10(a)和(b)所示, 其中横坐标为数据的实际层数, 纵坐标为数据的预测层数。 将光子总数用于BP神经网络模型训练后, 测试集的R2=0.978, RSME=2.56, 回归数据与曲线的拟合能力同样很强, 预测值与实际值的平均误差在 2.56层膜厚, 即51.2 μm。

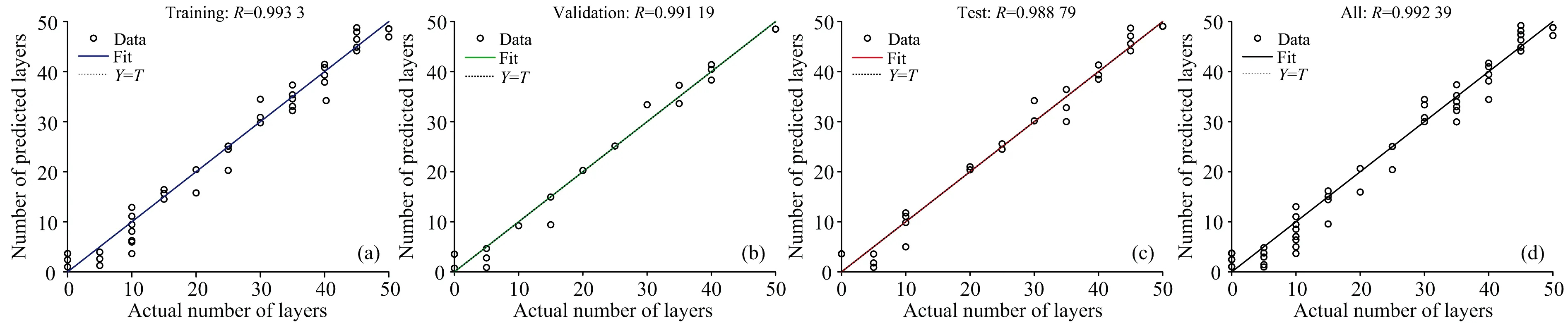
图10 (a)光子总数的训练集拟合度; (b)光子总数的验证集拟合度; (c)光子总数的测试集拟合度; (d)光子总数全部数据拟合度

3.5 数据分析结论

三种模式下的BP神经网络模型训练结果如表5所示。 对比三种数据处理的方案可知, 归一化处理对模型的拟合预测能力与误差控制能力均有较大的提升。

表5 训练结果比较

采取光子总数作为神经网络的输入时, 回归能力与误差控制能力只是略低于归一化处理的模型, 从数据点在拟合曲线上的分布可以看到, 光子总数模型存在个别数据点出现极端误差的情况, 相比之下, 归一化模型数据点的稳定性更佳, 没有出现极端的误差。 因此, 在本实验中, 将原始数据进行归一化与PCA主成分分析的预处理后, 再进行BP神经网络模型训练能够对塑料薄膜实现最佳的测厚效果, 平均误差为50 μm。

4 结 论

针对不明厚度的聚乙烯塑料薄膜制品, 利用X射线吸收光谱法采集数据, 先进行数据预处理, 如PCA主成分分析等, 并对模型进行训练优化, 最后将PCA降维后的数据作为BP神经网络模型的输入, 从而实现对塑料薄膜厚度的精确识别, 具有检测速度快、 识别精度高、 应用范围广的优点, 确定了一种单一材料塑料薄膜厚度的检测方法。 本文的具体内容如下:

(1)对10种厚度聚乙烯塑料膜的样本进行X射线吸收光谱采集, 其中每种样本采集40组数据, 同时还测量了40组背景光谱, 共440组原始数据用于模型训练。 并且随机抽取每种样本70%的数据作为训练集, 其余30%的数据作为测试集, 采取交叉验证的方式, 评估模型的准确率。

(2)对采集到的光谱数据进行预处理, 包括波段的选取以及PCA主成分分析特征提取, 达到信息降维的目的。

(3)将预处理后的数据作为BP神经网络的输入, 训练BP神经网络模型, 通过测试集的数据校验评估模型的厚度预测能力, 验证BP神经网路模型在该案例中的可行性。

(4)将原始数据进行归一化处理, 再经过PCA主成分特征提取以及BP神经网络训练, 通过测试集的数据校验评估模型的厚度预测能力。

(5)将原始数据进行光子数求和处理, 再经过BP神经网络模型训练, 通过测试集的数据校验评估模型的厚度预测能力。

(6)实验结果显示, 未归一化处理的数据经BP神经网络训练后的拟合优度为0.937, RSME值为4.46; 经过原始数据归一化处理后, BP神经网络训练后的拟合优度为0.984, RSME值为2.50; 经过光子数求和处理后, BP神经网络训练后的拟合优度为0.978, RSME值为2.56。 对比之后, 发现光谱数据归一化处理后得到的拟合曲线更优, 测量偏差更小。 将训练集数据作为BP神经网络模型的隐含层神经元, 通过与测试集的理想输出值的比较和统计, 得到归一化后的BP神经网络模型, 能将测量厚度误差控制在50 μm, 实现对聚乙烯薄膜厚度的检测。