利用紫外-可见光谱与平行因子分析法快速检测水体中多种有机磷农药的实验研究

黄 丽, 马瑞峻, 陈 瑜, 蔡 祥, 颜振锋, 唐 昊, 李艳芬

华南农业大学工程学院, 广东 广州 510642

引 言

农药在农业生产领域应用广泛[1-3], 根据其化学结构可分为四大类: 有机氯、 有机磷、 氨基甲酸酯和拟除虫菊酯, 其中有机磷农药占农药总量的34%, 中国每年使用有机磷农药高达9 100 t。 对农业生产来说, 有机磷农药能够为植物起到防治病虫害的作用, 实现增产保收, 带来巨大的经济效益。 然而, 有机磷农药的有效利用率却只有35%, 其余大部分都残留在土壤和水体环境中, 严重污染生态环境, 进而对人类健康造成威胁[4]。

由以上分析可知检测有机磷农药残留很有必要, 目前常用的检测方法有色谱法、 质谱法、 电化学法、 酶联免疫吸附法和酶抑制法等, 其中发展相对成熟的农药残留检测技术主要为色谱法和质谱法[5]。 谢美仪等用气相色谱法同时测出了环境水样和土壤中的6种有机磷农药, 加标回收率达到89.7%～109.9%[6]。 Cacho等利用气相色谱-质谱联用相结合, 对不同来源环境中的9种有机磷农药进行了测定, 农药回收率为85%～118%, 灵敏度为5～16 ng·L-1[7]。 色谱法具有检出限低、 检测灵敏度高以及定量分析准确等特点, 但需要在检测前进行样品的萃取和浓缩等耗时且复杂的前处理[8], 具有破坏性, 且仪器笨重, 价格昂贵, 无法实现现场快速检测。 因此, 如何实现有机磷农药残留的高效快速检测是当前农业生产生活中急需解决的问题。

近年来光谱技术发展迅速, 其中紫外-可见吸收光谱法只需通过对标准水样的吸收光谱进行分析建模, 无需添加化学试剂就可直接测定水样中物质的浓度, 其具备的高效快速和无二次污染等优点被广泛应用在各领域中[9]。 司绍博等利用紫外-可见吸收光谱结合化学计量学方法定量检测出了牛乳中的大肠杆菌总数, 所建立预测模型的决定系数R2高达0.96[10]。 赵明富等基于紫外-可见光谱技术, 利用主成分分析联合Fisher判别的方法建立的判别模型, 减少了对化工厂和溪水的水质类型判别时间[11]。 甄欢仪等利用紫外-可见光谱技术, 实现了对水体中马拉硫磷农药浓度的快速定量检测, 其预测模型的决定系数R2为0.99, 预测残差RPD高达24.16[12]。 但由于各种紫外-可见光谱仪测得的数据多为二维, 而传统的二维数据结合一阶校正方法的分解, 只能实现体系中单组分的定量检测。 且当多种有机磷农药共存时, 由于不同的有机磷农药大多包含相同或相似的化学结构, 在紫外-可见波段的吸收光谱相似度较高, 更是存在光谱重叠严重难以分辨的问题, 识别其组分和测定各组分的浓度相对困难[13]。 平行因子分析法(parallel factors analysis, PARAFAC)是一种针对三线性复杂数据的二阶校正方法, 只要数据的信噪比合适且选择正确的因子数目, 分解的结果可以反映真实的谱图。 如Lenhardt等采用荧光光谱结合PARAFAC分析方法识别出了4种不同成分的谷物面粉[14], 张晓亮等运用三维荧光光谱联合平行因子法及相关性分析, 对混合体系中的5类有机质进行了有效区分[15]。 但目前国内外研究大多为荧光光谱等获得的三维数据结合二阶校正方法对混合物进行分离检测, 由紫外-可见光谱仪等获取的二维数据结合PARAFAC方法检测混合体系中的多组分有机磷农药还未见报道。 故本文采用紫外-可见光谱技术获取不同种类和不同浓度的有机磷农药溶液的吸收光谱, 将测得的多个二维吸收光谱数据构建成不同的三维数据矩阵, 并结合平行因子分析方法实现了“数学分离”代替“化学分离”, 可以对多组分混合有机磷农药进行定性识别和定量检测。

1 实验部分

1.1 试剂及样本

实验所用试剂毒死蜱(Chlorpyrifos)、 甲基对硫磷(Methyl-Parathion)、 丙溴磷(Profenofos)均由华南农业大学资源与环境学院提供, 化学结构式如图1所示。 三种标准样品均以丙酮为溶剂配制浓度为100 mg·L-1的标准样液, 再以纯净水和农田水作为稀释剂配制实验样本, 其中纯净水为屈臣氏蒸馏水, 农田水取自华南农业大学农事训练中心, 使用前用5 μm滤膜进行过滤, 避免农田水体中的部分固体悬浮物降低光谱数据的信噪比, 影响本实验的检测精度[16]。

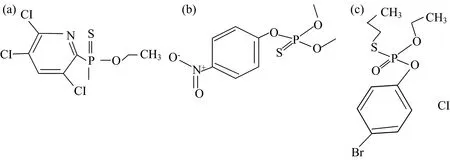
图1 三种农药化学结构式

校正集样本配制: 以纯净水为稀释剂, 配制有机磷农药的单组分、 2组分混合溶液实验样本。 单组分样本为毒死蜱溶液(简称: 毒)、 甲基对硫磷溶液(简称: 甲)、 丙溴磷溶液(简称: 丙), 2组分样本为毒死蜱和甲基对硫磷混合溶液(简称: 毒+甲)、 毒死蜱和丙溴磷混合溶液(简称: 毒+丙)、 甲基对硫磷和丙溴磷混合溶液(简称: 甲+丙), 共6组实验样本, 每组各30个样本, 各样本中三种有机磷农药的浓度范围均为0.1～5.9 mg·L-1(浓度梯度为0.2 mg·L-1), 合计180个样本, 编号为C1—C180, 其浓度见表1。

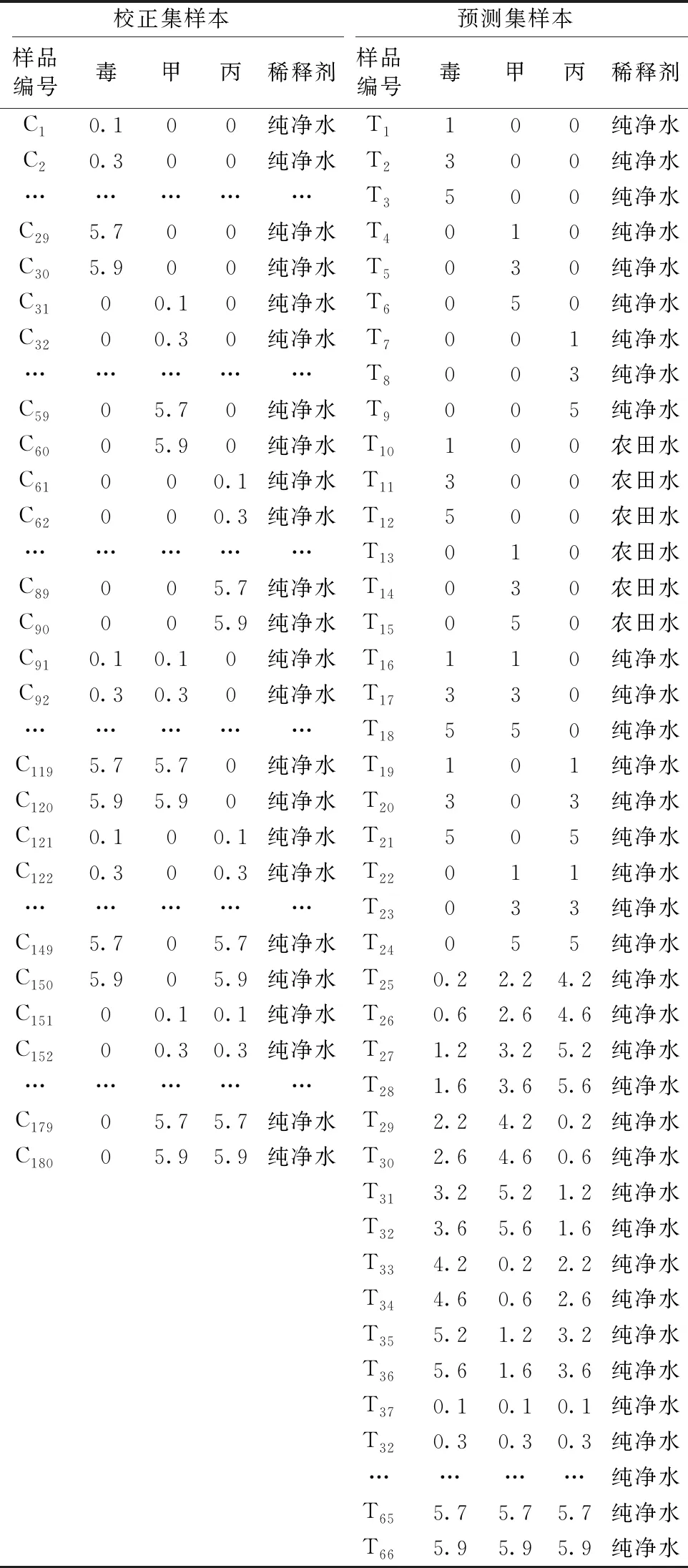
表1 校正集样本和预测集样本浓度(mg·L-1)

预测集样本配制: 以纯净水、 农田水为稀释剂, 配制有机磷农药的单组分、 2组分、 3组分溶液实验样本, 单组分样本为纯净水-毒死蜱溶液、 纯净水-甲基对硫磷溶液、 纯净水-丙溴磷溶液, 农田水-毒死蜱溶液、 农田水-甲基对硫磷溶液, 2组分样本为纯净水-毒死蜱和甲基对硫磷混合溶液、 纯净水-毒死蜱和丙溴磷混合溶液、 纯净水-甲基对硫磷和丙溴磷混合溶液, 3组分样本为纯净水-毒死蜱、 甲基对硫磷、 丙溴磷混合溶液(简称: 毒+甲+丙)。 预测集样本编号为T1—T66, 其浓度见表1(其中T37—T66样本中三种有机磷农药的浓度范围均为0.1～5.9 mg·L-1, 浓度梯度为0.2 mg·L-1)。

1.2 仪器

实验仪器采用美国海洋光学公司的Maya2000-Pro光谱仪, 光源为氘-钨卤灯组合光源(型号为DT-MINI-2-GS), 比色皿光程为50 mm。 光谱采集软件设置积分时间为9 ms, 平滑度为2, 选定光谱测量范围为200～900 nm, 共1 557个波长点, 每个样本扫描20次, 取平均值为最终光谱。

1.3 方法

1.3.1 PARAFAC分析法

在紫外-可见光谱检测中, 每个样本在J个波长变量下形成一个光谱向量,I个样本则形成一个光谱矩阵X(I×J), 由于有机磷农药化学结构的差异, 其不同种类或不同的农药混合都具有不同的吸收光谱, 本文将不同组分混合的有机磷农药溶液测得的吸收光谱数据作为背景K, 构成校正集三维矩阵X(I×J×K)再进行PARAFAC分解。 三维矩阵的构建与分解如图2所示。

PARAFAC分析法本质是一种基于交替最小二乘原理的迭代分解算法, 将三维矩阵X分解为三个二维载荷矩阵A、B、C的乘积, 其中G是N×N×N三维核心矩阵。 PARAFAC分解的目的是要使得残差eijk的平方和最小[17], 其算法的迭代过程为:

第一步: 确定模型的因子数F, 也就是混合体系中的组分数;

第二步: 初始化B和C的值, 其中B的维度为J×F,C的维度为K×F;

第三步: 以初始化后B、C的值和三维矩阵X来估算A的值;

K=1, 2, …,K

(1)

第四步: 以上一步得到A的估计值与C为基础, 估算B的值

(2)

第五步: 以上一步得到A的估计值与B为基础, 用同样的方法估算C的值;

(3)

重复第二步到第五步, 直至算法收敛为止。

PARAFAC模型用公式可以表示为

(4)

i=1, 2, …,I;j=1, 2, …,J;k=1, 2, …,K

式(4)中,xijk是三维矩阵X中的元素,F为模型估计的因子数,eijk是残差立体阵E(I×J×K)中的元素,aif、bjf、ckf分别为得分矩阵A、 载荷矩阵B和C矩阵中的元素, 且每个矩阵都具有实际的物理意义[18]。 本文中矩阵A为样本维, 与混合体系中各组分的浓度相关; 矩阵B为光谱维, 表现各组分的定性信息[19]; 矩阵C为样本堆维矩阵, 反映的是不同背景下各组分浓度的集中分布情况。 然后, 先建立得分矩阵A与已知参考浓度的线性回归模型, 对于预测集光谱矩阵, 结合校正集分解得到的两个载荷矩阵B、C进行PARAFAC分析, 得到预测集的预测得分, 进而利用所建立的线性回归模型对预测得分进行预测, 即可得到预测集的预测浓度。

1.3.2 核一致诊断法

在应用PARAFAC算法分解三维矩阵时, 首先需要确定体系的组分数, 本文采用核一致诊断法来确定模型的组分。 所谓“核一致”是指由Tucker3得到的核心矩阵与在理想情况下选取正确的因子数时所得核心矩阵的一致程度。

Core-consistency(%)=

(5)

式(5)中,F为模型的因子数,gdef是Tucker3计算得到的核心阵G的元素,tdef是理想情况下, 选取正确的因子数时所得核心矩阵T的元素, 通常采用阈值为0.6来判断因子数是否取值过大, 如果核一致值大于或等于60%, 则认为模型接近三线性, 若核一致值小于60%, 则体系偏离了三线性, 组分数选择不合理。

1.4 模型评价

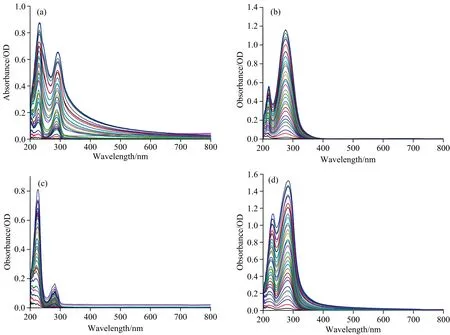
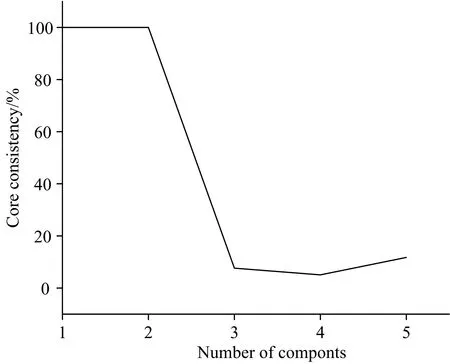
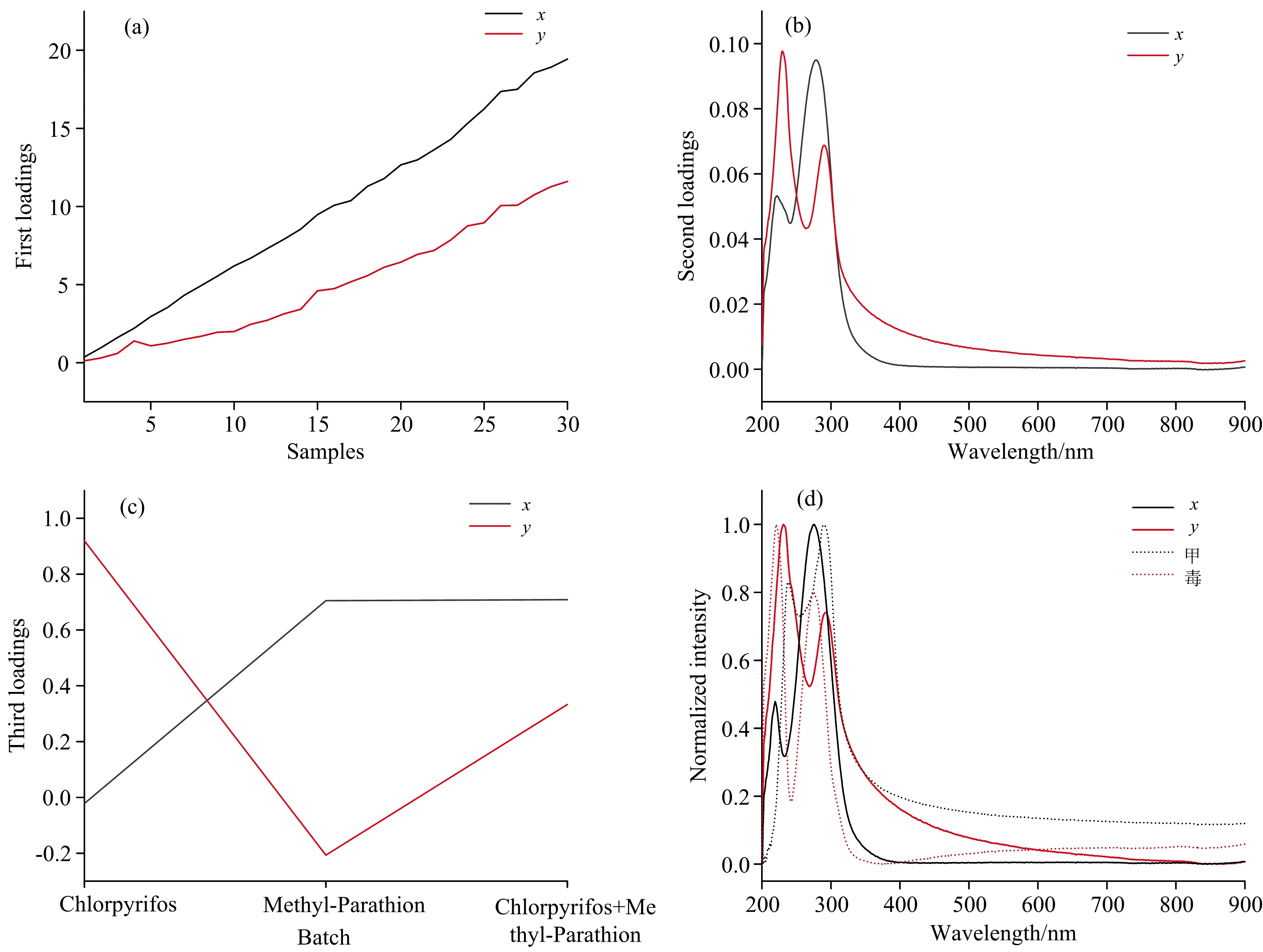
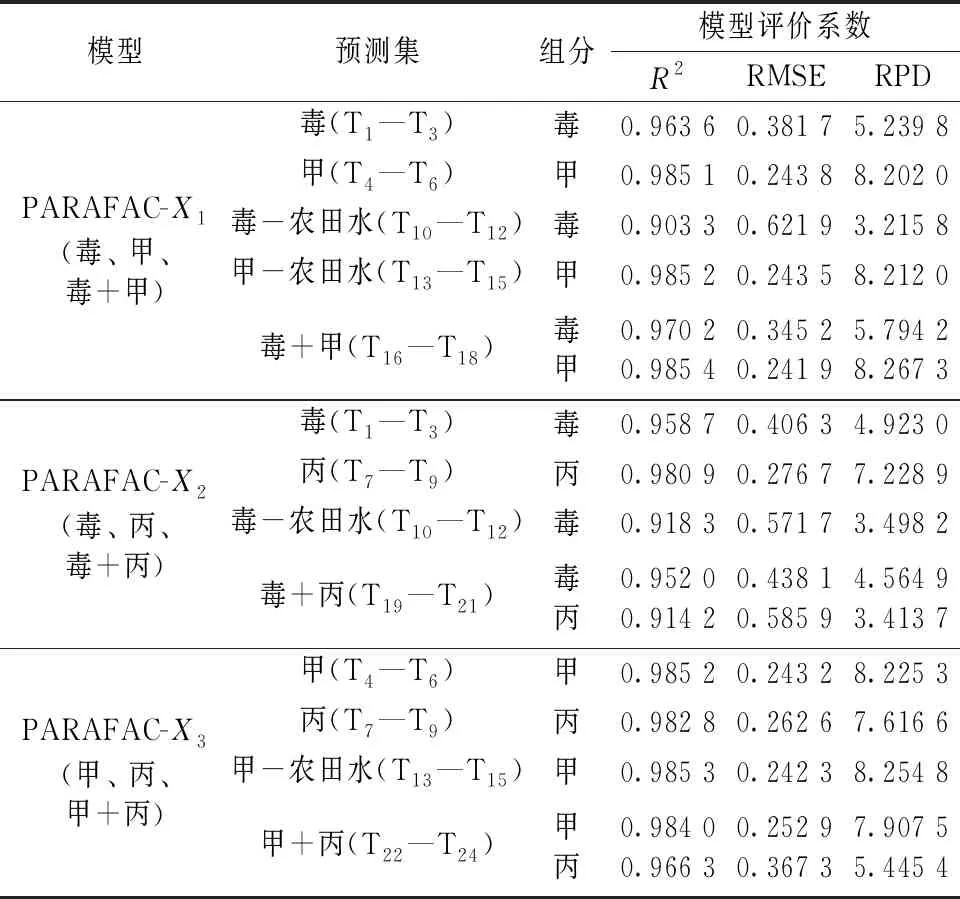
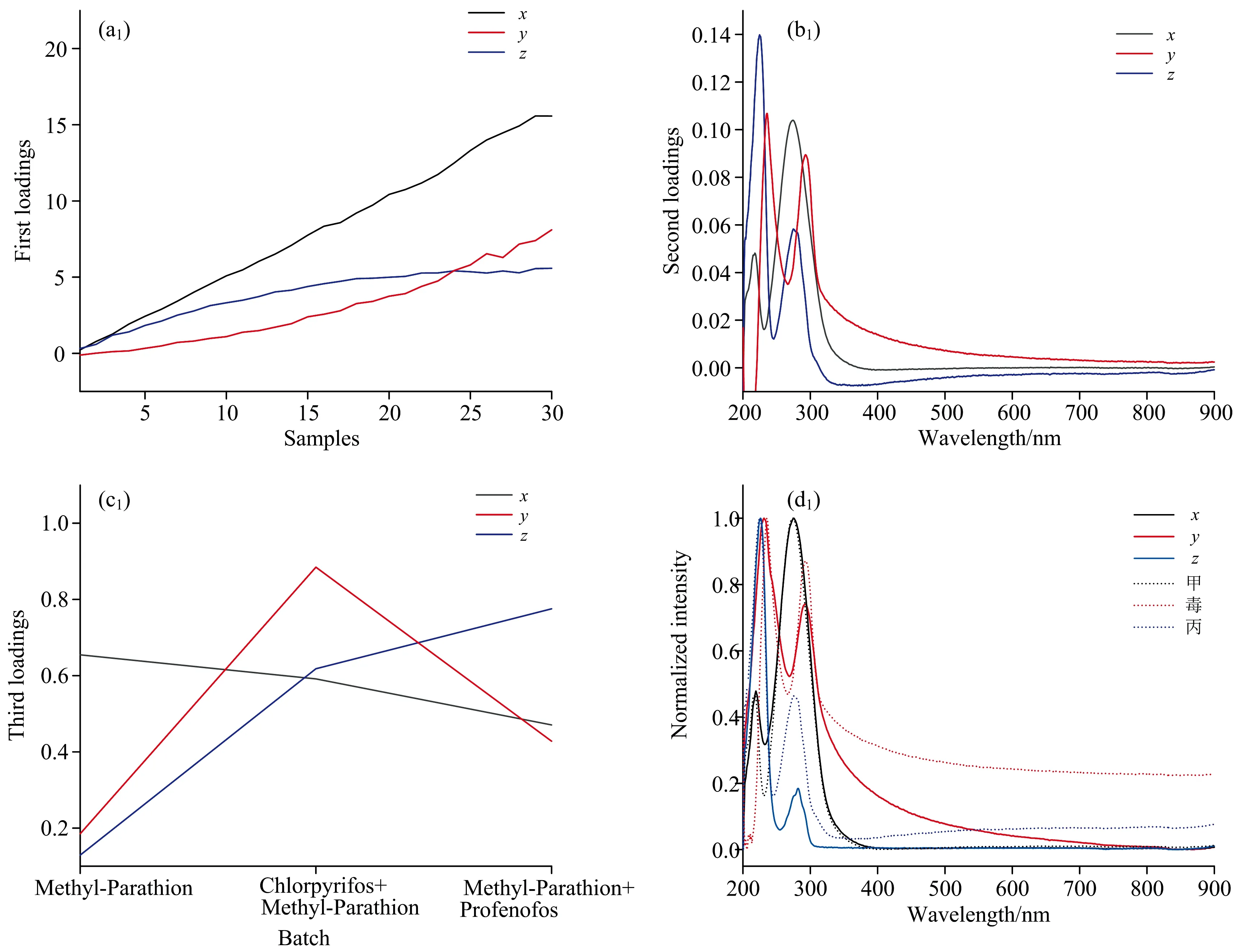
评价PARAFAC模型预测性能采用决定系数R2、 均方根误差RMSE和预测残差RPD。R2越大, 表明模型越稳定; RMSE越小, 表明模型精度越高[20], RPD是预测集参考值的标准偏差与预测均方根误差的比值, 反映了模型的分辨能力和稳健性, 如果2.5

2 结果与讨论

2.1 不同有机磷农药溶液的原始吸收光谱

校正集的6组实验样本(a—f)和预测集样本T37—T66(g)的原始光谱如图3所示。

图3 不同组分农药混合后的原始光谱图

由图3(a)、 (b)和(c)可知, 三种单组分有机磷农药的吸光度值随着浓度的增大而逐渐递增, 且整体光谱形状差异较大容易分辨, 毒死蜱的两个特征峰分别在229和290 nm处; 甲基对硫磷的两个特征峰分别在217和274 nm处; 丙溴磷的两个特征峰分别在221和281 nm处。 其中甲基对硫磷的吸光度值最大, 特征峰峰值最高为1.16, 其第二特征峰峰值大于第一特征峰峰值, 而毒死蜱和丙溴磷的最高峰值分别只有0.87和0.81, 第二特征峰峰值均小于第一特征峰峰值, 且丙溴磷溶液的两个特征峰值相差0.64, 差异最明显, 其吸收峰波长偏移量也最小, 光谱曲线整体显得“瘦高”。 以上性质可为多组分有机磷农药混合溶液经平行因子分解后的光谱维进行定性分析提供参考。

当不同的有机磷农药按照相同的浓度比例混合时, 得到的吸收光谱如图3(d)、 (e)、 (f)和(g)所示, 由图可知, 多组分有机磷农药混合溶液的吸收光谱曲线几乎完全重叠, 且存在吸收峰偏移、 噪声干扰等问题, 用传统的一阶校正方法无法对其中的农药组分进行分辨。 其中2组分混合农药的光谱最大吸光度值为1.52, 3组分混合农药的光谱最大吸光度值为1.69, 均大于各单组分农药溶液的最大吸光度值, 符合混合体系中不同组分吸光度的加合性, 且随着混合体系中各组分浓度的增加, 吸光度值呈现递增趋势, 浓度与吸光度之间呈现较好的线性关系, 仍然符合朗伯-比尔定律, 具备吸收光谱定量分析的理论基础。

由图3(d)、 (f)和(g)可知, 多组分混合溶液中含有甲基对硫磷的吸收光谱图, 其第二特征峰峰值均高于第一特征峰峰值。 而不含甲基对硫磷的毒+丙混合溶液的吸收光谱图3(e), 其第二特征峰峰值小于第一特征峰峰值, 与单组分的毒死蜱和丙溴磷的光谱具有相同的变化趋势。 由此可知, 同等程度下这3种有机磷农药混合溶液中甲基对硫磷具有较大的光谱贡献。

2.2 应用PARAFAC算法分离2组分混合有机磷农药

将校正集中毒死蜱、 甲基对硫磷、 毒死蜱和甲基对硫磷混合溶液获得的光谱数据构造为三维数据阵列X1, 采用PARAFAC算法进行分解, 首先根据核一致诊断法判断因子数, 如图4为核一致值与因子数的变化趋势, 随着因子数的增加, 核一致值逐渐减小, 当因子数大于2时, 核一致值急剧下降至低于60%, 此时模型已偏离三线性, 表示因子数选择不合理, 结合混合体系中的实际情况可以确定因子数为2。

图4 核一致诊断分析结果

选定因子数为2对三维矩阵X1进行PARAFAC分析, 得到一个得分矩阵和两个载荷矩阵如图5(a—c)所示, 分别对应样本维矩阵A、 光谱维矩阵B、 样本堆维矩阵C。

图5 2组分(X1)有机磷农药的PARAFAC分解结果

对比图5(b)和图3(a)、 (b)的光谱曲线可以看出, 2个因子的曲线分别包含2种组分各自的吸收峰, 其中因子x的两个特征峰分别位于217和278 nm处, 因子y的两个特征峰分别位于229和289 nm处, 且两个因子的吸收峰出现顺序为x先于y; 图5(c)则对应样本堆维, 因子x在毒死蜱处值约为0, 而在甲基对硫磷处为最大值, 因子y在甲基对硫磷处值约为0, 在毒死蜱处为最大值, 两因子在毒死蜱+甲基对硫磷处都为中间值。 综合以上分析可知, 因子x对应为甲基对硫磷, 因子y对应为毒死蜱。 为了进一步说明算法分解得到的光谱与真实光谱的吻合程度, 分别将光谱维与单组分农药的真实光谱进行归一化处理, 消除数据之间的量纲和取值范围差异的影响[21], 结果如图5(d)所示(图中单组分农药的真实光谱用实线表示, PARAFAC分解得到的光谱用虚线表示), 可以看出分解得到各组分的光谱与真实光谱相似度较高, 基本吻合, 可以实现2组分毒死蜱+甲基对硫磷混合溶液的定性分析, 即体现了PARAFAC分析方法的“二阶优势”[13, 17]。

分别将纯净水中单组分的毒死蜱溶液(T1—T3)、 甲基对硫磷溶液(T4—T6), 农田水中单组分的毒死蜱溶液(T10—T12)、 甲基对硫磷溶液(T13—T15), 纯净水中毒死蜱和甲基对硫磷混合溶液(T16—T18)测得的光谱数据分别作为预测集, 与由校正集分解得到的载荷矩阵B、C进行PARAFAC分析, 得到预测得分矩阵。 再将校正得分数据分别结合毒死蜱、 甲基对硫磷各自的真实浓度构建线性回归模型, 记为PARAFAC-X1, 利用所建立的线性回归模型对预测得分进行预测, 得到预测集的预测浓度。

将校正集中毒死蜱、 丙溴磷、 毒死蜱和丙溴磷混合溶液获得的光谱数据构造为三维数据阵列X2, 根据核一致诊断法和实际情况确定因子数为2, 采用PARAFAC算法进行分析, 发现分解出的毒死蜱和丙溴磷的光谱与实际光谱基本吻合, 可以实现对毒+丙混合溶液的定性分析, 接着建立毒死蜱和丙溴磷的线性回归模型, 记为PARAFAC-X2。 进一步地, 利用所建立的线性回归模型分别对纯净水-毒死蜱、 纯净水-丙溴磷、 农田水-毒死蜱、 纯净水-毒死蜱和丙溴磷混合溶液的光谱进行预测, 得到预测集的预测浓度。 同样地, 将校正集中甲基对硫磷、 丙溴磷、 甲基对硫磷和丙溴磷混合溶液获得的光谱数据构造为三维数据阵列X3, 根据核一致诊断法和实际情况确定因子数为2, 采用PARAFAC算法分解并建立模型, 记为PARAFAC-X3, 建模和预测方法同上。 三个模型得到的预测结果见表2。

表2 PARAFAC模型预测结果(2组分)

如表2所示, 构建的三个模型中, 当校正集中包含预测集所有的农药信息时, PARAFAC算法可以识别出体系中的各组分并进行定量分析; 当预测集中存在校正集不存在的干扰成分(农田水)时, 依然可以识别出其中感兴趣的组分并进行测定, 体现了算法的“二阶优势”, 其决定系数R2都大于0.9, 预测残差均大于3, 模型的预测效果较好, 表明2组分模型可以对未知的单组分农药溶液和2组分混合农药溶液进行定性分析和定量检测。

当采用同一模型对不同的数据集进行预测时, 如模型PARAFAC-X1对纯净水中的毒死蜱、 农田水中的毒死蜱、 纯净水中毒+甲混合溶液中的毒死蜱, 即使是相同的有机磷农药, 得到的预测精度也有差异, 这是预测集本身数据的差异性造成的。 同样地, 当采用两个不同的模型对同一数据集进行预测时, 如模型PARAFAC-X1和PARAFAC-X2分别对纯净水和农田水中的单组分的毒死蜱进行预测, 得到的预测精度也略有差异, 这是因为不同的模型对同一预测集光谱变化的覆盖程度不同造成的[17]。

当预测集中只有单组分农药时, 模型PARAFAC-X1和PARAFAC-X2对农田水中毒死蜱的预测精度要低于纯净水中的, 这是因为农田水体中的部分杂质对毒死蜱分子产生了干扰, 而模型PARAFAC-X1和PARAFAC-X3对甲基对硫磷的预测精度影响却不大, 其预测精度甚至要更好, 可能的原因是农田水体中某些硝酸盐在220 nm处有明显的吸收峰[22], 这与甲基对硫磷的第一吸收峰位置相近, 其部分光谱吸收被归为了甲基对硫磷的光谱吸收, 提高了甲基对硫磷的吸收光谱强度, PARAFAC模型对光谱特征明显的数据集有较好的预测能力。

当预测集为2组分有机磷农药时, 构建的三个模型对毒+甲、 毒+丙、 甲+丙混合溶液中的各组分均达到了定量检测要求, 说明PARAFAC分析方法可实现水体中2组分有机磷农药的分离与预测。

2.3 应用PARAFAC算法分离三组分混合有机磷农药

将校正集中甲、 毒+甲、 甲+丙测得的光谱数据构造为三维数据阵列X4, 根据核一致诊断法和混合体系中的实际情况选定因子数为3对三维矩阵X4进行PARAFAC分析, 得到一个得分矩阵和两个载荷矩阵如图6(a1—c1)所示, 图6(d1)为各单组分农药的真实光谱与光谱维b1归一化处理后的结果。

图6 3组分有机磷农药的PARAFAC分解结果

由图6(d1)可知, PARAFAC分解得到3组分有机磷农药的光谱与各自的真实光谱基本重合, 实现了对3组分有机磷农药混合溶液中毒死蜱、 甲基对硫磷、 丙溴磷的定性分析。 根据光谱维b1、 样本堆维c1和图6(d1), 可以判断出因子x、y、z分别为甲基对硫磷、 毒死蜱、 丙溴磷。 将校正得分矩阵A1的数据分别结合毒死蜱、 甲基对硫磷、 丙溴磷各自的真实浓度构建线性回归模型, 得到的3组分模型记为PARAFAC-X4。 进一步地, 利用所建立的模型对纯净水中毒死蜱、 甲基对硫磷、 丙溴磷三种农药混合溶液的光谱进行预测, 得到的预测结果如表3所示。

表3 PARAFAC模型预测结果(3组分)

将毒死蜱、 甲基对硫磷、 丙溴磷三种有机磷农药都作为建模元素来参与回归计算, 这样模型中包含了三种农药的背景信息, 扩大了模型覆盖范围, 有利于多组分农药的分析测定。

由表3可知, 采用模型PARAFAC-X4对3组分混合溶液进行预测, 对毒死蜱和甲基对硫磷的预测精度都较高, 决定系数R2都大于0.9且预测残差均大于3。 其中对甲基对硫磷的预测残差值高达9.844 3, 这是因为校正集中包含更多甲基对硫磷的信息, 其在混合体系中的光谱贡献最大。 但是对丙溴磷的预测结果达不到定量检测的要求, 经分析认为此现象是因为在3组分混合溶液中, 同等浓度的毒死蜱、 甲基对硫磷溶液的整体吸收光谱强度水平相近, 都显著高于丙溴磷在同等浓度下的吸收光谱强度, 降低了混合体系中丙溴磷所占比重, 导致其光谱贡献最小, 以致算法对3组分混合体系中丙溴磷的预测结果不理想。

3 结 论

(1)针对多组分有机磷农药光谱重叠严重难以区分的问题, 本文以毒死蜱、 甲基对硫磷、 丙溴磷三种有机磷农药为研究对象, 将二维紫外-可见光谱与二阶校正方法-平行因子分析法相结合, 实现了“数学分离”代替“化学分离”。

(2)本文所建立的2组分模型PARAFAC-X1、 PARAFAC-X2、 PARAFAC-X3均实现了对有机磷农药的单组分溶液、 2组分混合溶液和存在干扰(农田水)的单组分溶液定性分析和定量检测, 预测集决定系数R2都大于0.9, 预测残差也大于3。 突出了PARAFAC算法的“二阶优势”。

(3)本文所建立的3组分模型PARAFAC-X4实现了对3组分混合溶液中毒死蜱、 甲基对硫磷、 丙溴磷的定性分析, 其中对毒死蜱和甲基对硫磷都达到了定量分析要求, 只有丙溴磷不能定量检测, 针对此问题后续还有待进一步研究。

(4)下一步的工作中, 可以通过改进算法, 或将不同的二阶校正方法如N维偏最小二乘法、 交替三线性分解应用于多组分有机磷农药的定性分析与定量检测, 建立稳健性与预测性能都更好的模型, 以提高模型的预测精度。