数学定理在高中物理解题中的应用

摘 要：高中物理与数学两个学科之间有着密切的联系，利用勾股定理、韦达定理、正弦定理以及余弦定理等数学定理能够有效辅助高中物理解题，使物理题化繁为简，帮助学生快速找到解题突破口，进而高效完成物理解题.但数学定理众多，因此，需在实际物理解题过程中正确审题，选择合理的数学定理进行解题，以避免步入解题误区.鉴于此，本文主要内容是分析与研究数学定理在高中物理解题中的应用，以期为广大高中物理教师与教研人员提供参考与借鉴.

关键词：数学定理；高中；物理；解题

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2023）28-0118-03

收稿日期：2023-07-05

作者简介：杨继虾（1992.4-），甘肃省秦安人，研究生，中学一级教师，从事高中物理教学研究.

高中物理知识具备较强的逻辑性和抽象性，若想快速、正确解题，便可以利用数学定理进行辅助解题.因此，为有效提高学生解题能力，本文主要探析数学定理在高中物理解题中的应用.

1 高中物理解題中应用数学定理的先决条件分析

1.1 加强对基本概念的掌握

学生在解析物理题目时往往因对物理基本概念掌握不牢靠，导致在审题或理解过程中出现各种各样的失误，这样不仅会直接影响数学定理的应用效果，同时也在一定程度上降低了高中物理解题准确率和效率.因此，需要结合实际情况做好以下几方面内容：第一方面，需要确保学生有效明确物理概念，尤其是物理知识中部分字面相似的概念，从根本上明确其本质和差异性.例如速度与加速度，虽然两者之间仅有一字之差，但在物理题目中的意义却截然不同，加速度是指物体运动过程中的状态变化快慢，速度是指在特定距离中物体的变化快慢；第二方面，加强学生对不同物理量之间关联性的理解，确保其在实际解题过程中能够灵活、正确地利用不同物理量之间的关系，达到高效率、高准确率的解题效果，从而为有效利用数学定理解析高中物理题目奠定重要基础^[1].

1.2 落实细致性审题效果

在高中物理力学相关的问题中，往往会在一个题目场景内以多个不同物体描述受力变化，在此类题目中，部分题目并不会展示物理变化全过程，而有的题目则会展示物理变化全过程.因此，为确保数学定理在高中物理力学相关问题中的应用合理性与准确性，则首先需要学生结合实际情况，加强对题目的解析与审查，在实际审题过程中落实细致性的审题效果.在审题过程中应当注意一下几方面内容：第一方面，在解析任何一个高中物理力学题目前，都需要学生结合实际情况基于题目所给信息对物体受力情况进行全面、系统的分析，其中也包括明确单位是否统一等基本问题，以此为后续顺利应用数学定理奠定基础；第二方面，需要深化抽象思维的运用，从而有效明确题目中的所指向的研究对象，达到以定量分析变量的效果，并将数学定理套入至物理图景中，使其形成以物理题目为背景的数学习题，以此有效降低高中物理题目实际解析期间的难度；第三方面，为有效加强实际解题过程中的规范性与标准性，为后续数学定理的顺利应用提供依据，则需要学生在实际解题过程中将所有已知参数、条件等信息标注在示意图内，而后结合题目内容，对不同时间下运动状态情况、基本受力情况等进行分析，以此实现利用数学定理加强解题目标和已知条件之间的关联性，充分发挥数学定理在高中物理解题过程中的媒介服务作用^[2].

2 数学定理在高中物理解题中的应用分析

2.1 基于勾股定理的高中物理解题策略

对于高中阶段的学生而言，其通过初中阶段的系统性学习已经能够在实际解题过程中熟练运用勾股定理.同时，在长期对勾股定理的运用和理解后，高中阶段学生已经能够有效将勾股定理运用于力的分解、速度分解等相关高中物理题目中.为进一步加强高中阶段学生在物理习题实际解答过程中运用勾股定理的灵活性与准确性，教师要为学生创设科学合理且富有针对性的问题情景，确保学生能够在问题情境中达到对勾股定理活学活用的应用效果，潜移默化地培养学生在日常物理解题过程中利用勾股定理进行解题的意识与习惯.

以下述高中物理选择题为例，如图1所示，滑板运动员运动状态图.一名滑板运动员在滑坡中沿着水平方向前进后，又落到带有一定倾斜角度的滑坡上.若滑坡倾斜角度为θ，当滑板运动员在滑坡中沿着水平方向飞出时，此时水平速度数值为V₀，在滑板运动员运动过程中全程忽略空气阻力且重力加速度数值为g，则以下选项那个是正确的（）.

A.当滑板运动员初次落到滑坡上时，其速度大小为

具体解析过程如下，由于该题中滑板运动员所产生的运动为平抛运动，因此可以通过12gt²V₀t计算tanθ，即tanθ=gt2V₀，通过公式变换能够的到t=2V₀tanθg.在已知t的条件下，能够有效计算滑板运动员在竖直方向中的速度，以V_S表示.由于滑板运动员在竖直方向上的运动属于自由落体运动， 因此通过自由落体的瞬时速度计算公式V=gt，可知V_S=2V₀tanθ，滑板运动员初次抵达滑坡时的速度为V.通过利用勾股定理能够得出，V=V²₀+（2V₀tanθ）²=V₀1+4tan²θ.由此可知，滑板运动员的竖直位移为C_竖=2V²₀tan²θg，其水平位移为C_水=2V²₀tanθg.通过勾股定理A²+B²=C²可以对滑板运动员落到滑坡上的位置C进行计算，即C=C²_竖+C²_水=2V²₀tanθ1+tan²θg.通过上述解题过程可以得出，正确答案为AC.

2.2 基于正弦定理的高中物理解题策略

对于数学定理中的正弦定理而言，其主要描述的内容为三角形中角度和边长之间的关系.在高中物理解题过程中，可以结合实际情况通过灵活运用正弦定理将其中的边长等效为作用力，从而达到基于正弦定理快速定位高中物理题目中各个定量参数之间的关系，以此为高中学生顺利解题提供重要依据.一般情况下，正弦定理多用于高中物理题目中的受力分析题.具体应用思路为如下：首先学生需要结合高中物理基础知识对物体受力情况进行分析，而后利用数学几何知识明确物理模型中的角度大小，最后结合上述分析结果利用正弦定理形成角度与力之间的等式关系^[3].

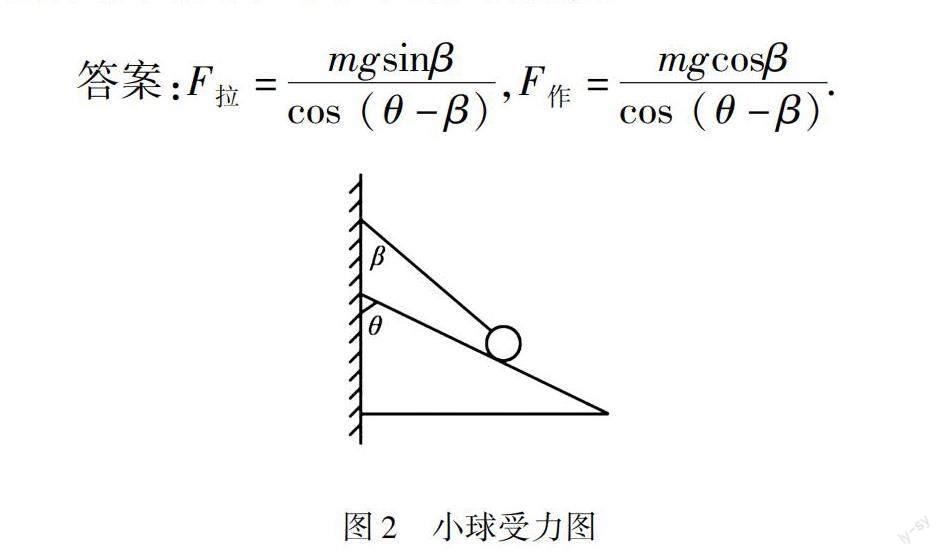
以下述高中物理計算题为例，如图2所示，小球受力图.通过对图2分析可知，一根绳子的一端连接了一个质量为m的小球，而另一端则固定在墙体中.图中倾斜面的摩擦力为0，小球放置在倾斜面上.其中，竖直墙体与倾斜面之间的夹角为θ，竖直墙体与绳子之间的夹角为β.通过对上述内容进行分析，求倾斜面对小球的作用力与绳子对小球的拉力数值.

答案：F_拉=mgsinβcos （θ-β），F_作=mgcosβcos （θ-β）.

2.3 基于余弦定理的高中物理解题策略

对于数学定理中的余弦定理而言，其通常用于对不规则三角形内角、边长等相关方面的求解过程中.基于余弦定理特点，在高中物理解题过程中，可以通过余弦定理解析物理题目中的角度、距离等相关问题^[4].为确保学生能够在高中物理解题过程中熟练运用余弦定理，并可以根据题目具体情况的不同以灵活性、合理性的原则应用余弦定理，则需要结合实际情况做好以下两方面内容：第一方面，需要阶段性的带领学生回忆并理解余弦定理内容、表达公式等相关知识点，以此有效巩固学生对余弦定理知识的记忆，防止学生在实际解题过程中出现知道该题目需要利用余弦定理，但却忘记余弦定理的相关知识与表达公式；第二方面，为进一步加强学生在高中物理解题过程中对余弦定理的应用熟练度，教师则应当结合实际情况阶段性地带领学生完成优质经典例题，需要确保例题中有效涵盖余弦定理相关内容，通过解析经典例题并逐步拆分其中解题步骤，使学生亲身感受高中物理基础知识和余弦定理的融合效果，确保学生能够有效发现在高中物理解题过程中通过利用数学定理可以大幅降低解题难度，从而使其在日后学习与解题过程中主动利用数学定理完成高中物理相关习题^[5].

综上所述，在高中物理解题期间，若想顺利将数学定理灵活应用至物理题目中，不仅需要高中阶段学生灵活掌握多样化的数学定理，同时也需要其具有夯实的高中物理基础知识，这样才能够确保学生在实际解题过程中将高中物理基础知识和数学定理进行有机结合，从而达到良好的利用数学定理辅助高中物理解题的效果.

参考文献：

[1] 刘长强.数学定理在高中物理力学解题中的有效应用研究[J].中学理科园地，2022，18（3）：65-68.

[2] 季剑峰.高中物理变力做功问题的妙解：以链条运动为例[J].高中数理化，2020（4）：28.

[3] 纪桂英.物理解题中数学定理的应用策略[J].中学生数理化（学习研究），2022（10）：51-52.

[4] 马永祯.数形结合思想在高中数学教学中的运用策略研究：以《简单的线性规划问题》为例[J].考试周刊，2021（77）：82-84.

[5] 蒋国俊.巧用正弦定理解决动态平衡问题[J].物理教师，2021，42（6）：94-95.

[责任编辑：李 璟]