一种基于卡尔曼滤波定位解算方法的研究

刘明阳，李 斌

一种基于卡尔曼滤波定位解算方法的研究

刘明阳1,2，李 斌1,2

（1 中国电子科技集团公司第二十研究所，西安 710068；2 陕西省组合与智能导航重点实验室，西安 710068）

GPS利用卫星发射的无线电信号，通过计算卫星与GPS接收机之间的相对位置，进而确定出用户接收机在地球上的位置，可以为用户接收机提供实时的定位、测速和授时等服务。传统接收机通过最小二乘法进行定位解算，接收机坐标容易发生较大的跳动。通过利用卡尔曼滤波原理，根据接收机的运动特点建立模型，利用每次导航解算结果之间的联系，对定位结果进行平滑，消除由于最小二乘算法结果相对独立而产生的定位抖动误差。通过定位试验结果表明，所设计的定位解算算法具有良好的定位效果。

GPS；卡尔曼滤波；定位结果分析

0 引言

因为GPS具有信号覆盖范围广泛、全天候实时可用、用户接收机定位精度高等特点，所以在船舶、飞机导航、用户自主导航和城市交通智能管理等领域有较为广泛的应用[1-3]。最小二乘算法在导航接收机的定位解算领域有着较为广泛的应用，但是通过最小二乘法求解的定位结果容易受观测伪距误差的影响而产生较大的跳动[4]。本文通过利用卡尔曼滤波原理，消除由于最小二乘算法结果相对独立而产生的位置抖动。

1 卡尔曼滤波原理

系统的观测方程如式（1）所示[5]

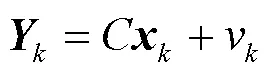
卡尔曼滤波状态方程如式（2）所示[6]

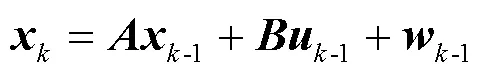
卡尔曼滤波的系统模型如图1所示[7-8]。

卡尔曼滤波递推算法如图2所示，卡尔曼滤波递推算法分为两部分，预测与校正。

图1 卡尔曼滤波的系统模型

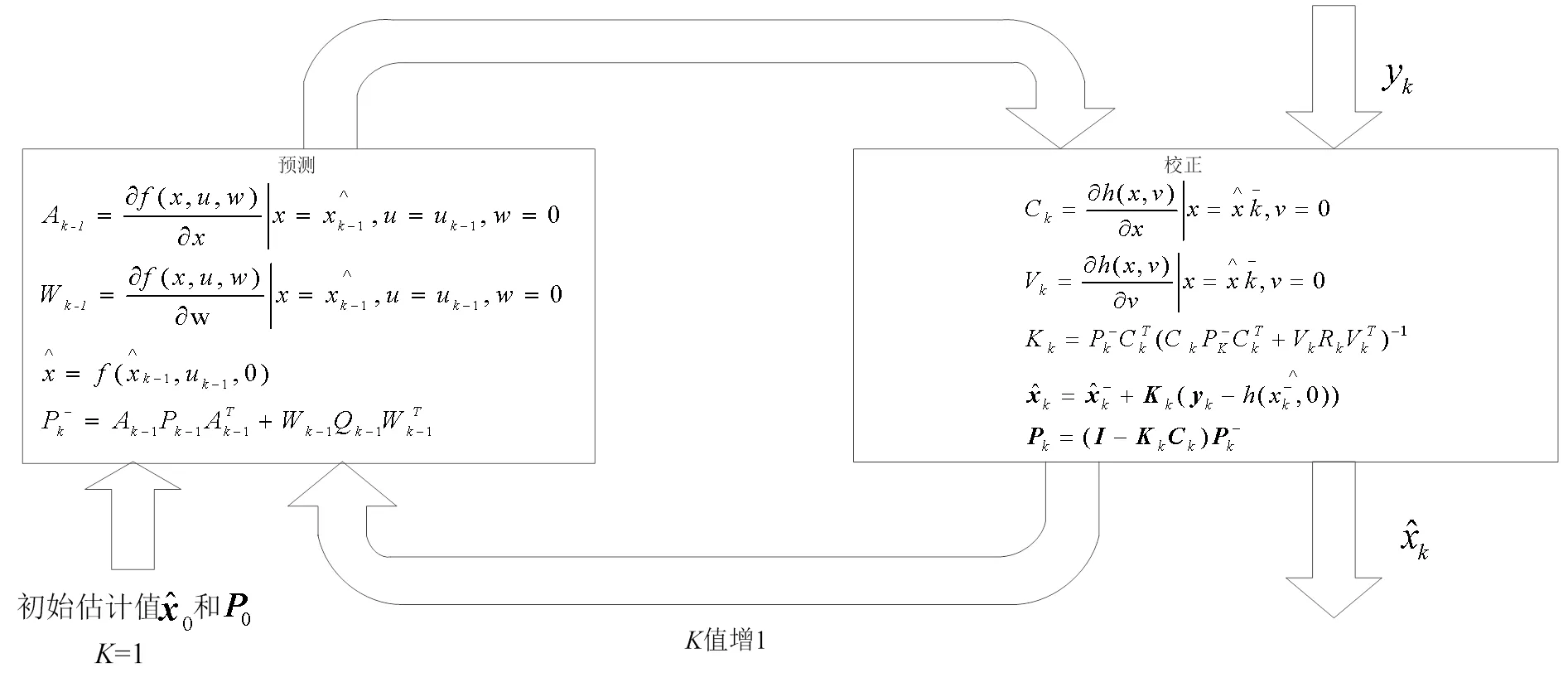
图2 卡尔曼滤波的递推算法

2 卡尔曼滤波解算算法

卡尔曼滤波在GPS接收机解算定位中的算法流程如图3所示。首先利用状态方程预测接收机当前的位置、速度和钟差等状态；然后，根据这一状态先验估计值以及卫星星历所提供的卫星位置与速度，卡尔曼滤波器就可以预测GPS接收机对各颗卫星的伪距与多普勒频移值，而这些测量预测值与接收机的实际测量值之间的差异形成测量残余；最后，卡尔曼滤波的校正过程通过处理测量残余而得到系统状态估计值的校正量及其校正后的最优 估计[10]。

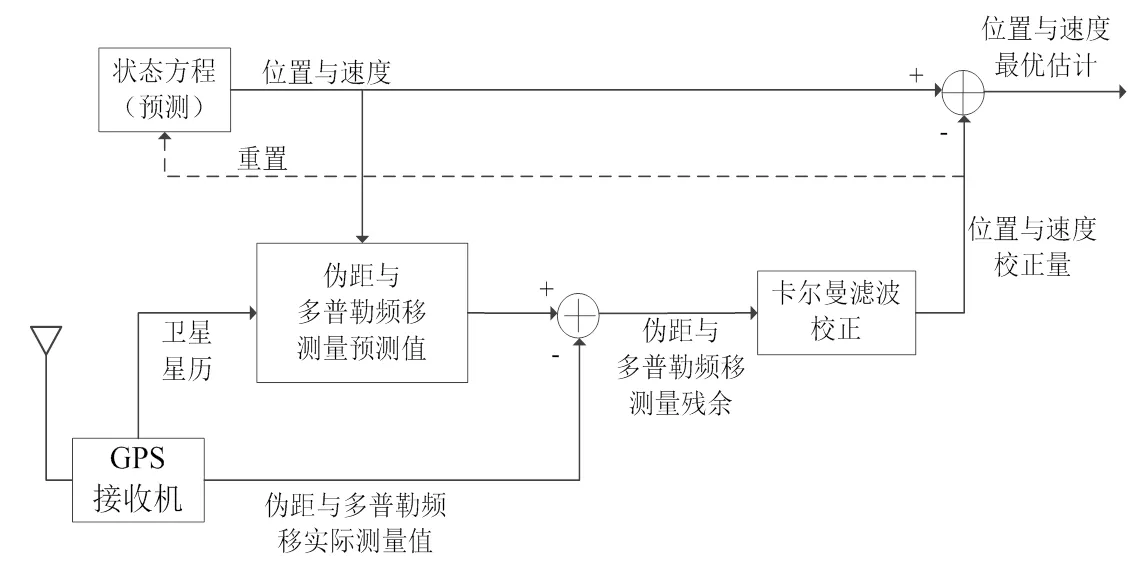
图3 GPS接收机卡尔曼滤波解算流程

伪距观测方程式如式（3）所示

在每一解算时刻，将式（3）计算所得伪距观测量作为卡尔曼滤波器观测方程中的观测量，根据接收机的运动方式建立状态方程，利用前一时刻的接收机位置信息作为状态方程的输入量。根据卡尔曼滤波算法计算出当前时刻的接收机位置信息。

在卡尔曼滤波算法处理过程中，根据用户运动状态的不同来确定系统的状态方程。根据接收机的运动状态主要分为接收机静止和匀速运动。

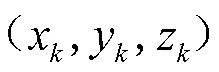
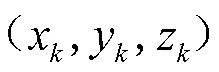
GPS接收机的系统状态方程可写为

可以看出，GPS接收机在利用卡尔曼滤波定位解算时，系统状态方程为线性方程，无需进行线性化处理。而系统的伪距方程为非线性方程，需进行线性化处理。

设定定位解算方程如式（7）所示

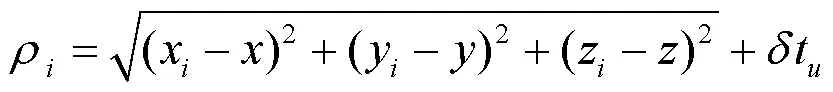
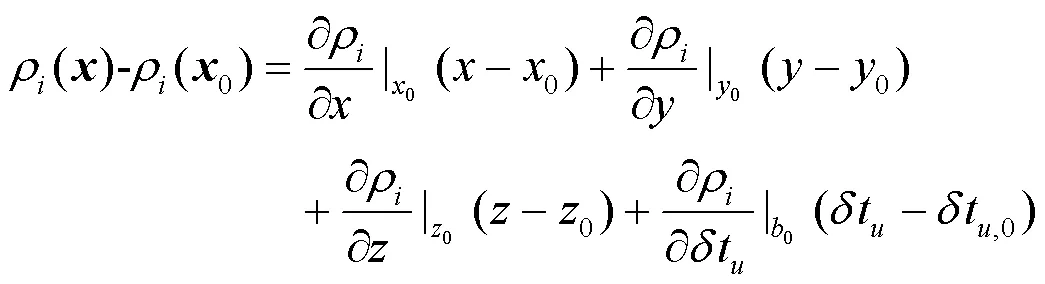
式（8）就可以改写为

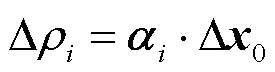
进行线性化处理后的伪距方程写成矩阵形式为

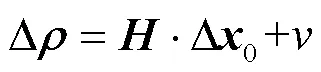
式中，为经过线性化处理后的观测矩阵。由此，得到两个线性方程组，可以进行卡尔曼滤波解算。

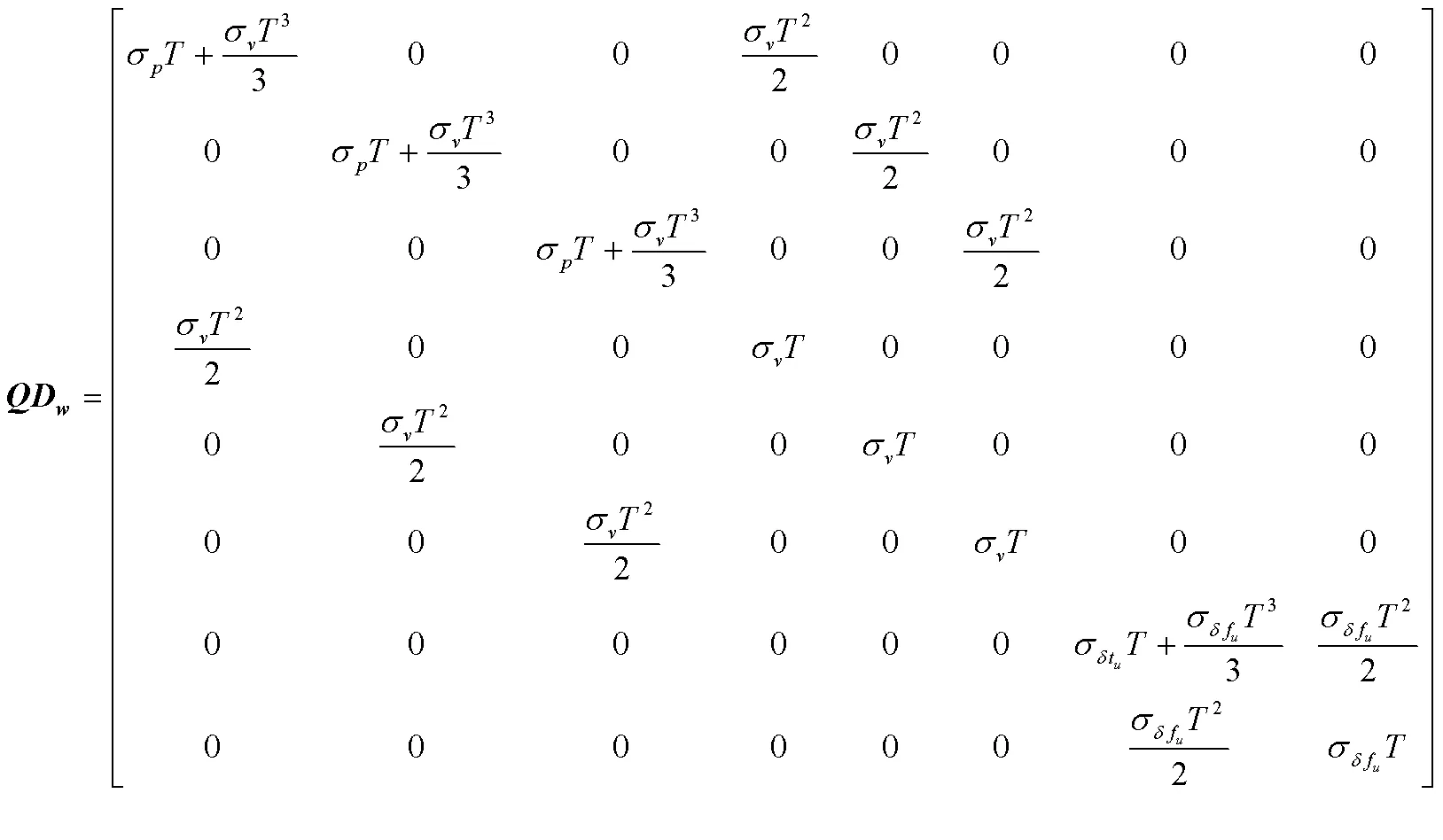
3 卡尔曼滤波定位结果

为了验证与分析最小二乘法的定位解算结果，使用GNS8451型信号模拟器发送GPS信号，模拟接收机在静止状态下所收到的卫星信号，共模拟16颗卫星的信号用于接收机进行定位解算，设定接收机模拟位置为：

经度88.959 545 264°纬度108.069 017 231°

高度402.291 043 892 m

在进行最小二乘法的定位解算时采用了和GNS8451型信号模拟器播发场景一致的电离层误差、对流层误差等误差的误差模型，这样可以抵消误差，提高了试验结果定位精度。

对模拟信号进行捕获跟踪，接收机每秒进行一次定位解算，进行600次定位解算，定位时采用了卡尔曼滤波与最小二乘解算两种方法分别进行解算定位，即根据观测到的伪距与提取出来的卫星发送时刻，分别送入卡尔曼滤波模块与最小二乘模块，分别解算出定位结果，进行对比。在进行最小二乘法的定位解算时采用了和GNS8451型信号模拟器播发场景一致的电离层误差、对流层误差等误差的误差模型，这样可以抵消误差，提高了试验结果定位精度。

选取了其中的80次定位解算结果如图4所示，图中横坐标为定位次数，纵坐标为定位误差。为了对比卡尔曼滤波与最小二乘解算的结果，图4中粗实线为采用卡尔曼滤波解算得到的定位结果，细实线为采用最小二乘解算的定位结果。可以看出，在每两次定位结果之间，卡尔曼滤波的定位结果的明显要好于最小二乘解算的结果。

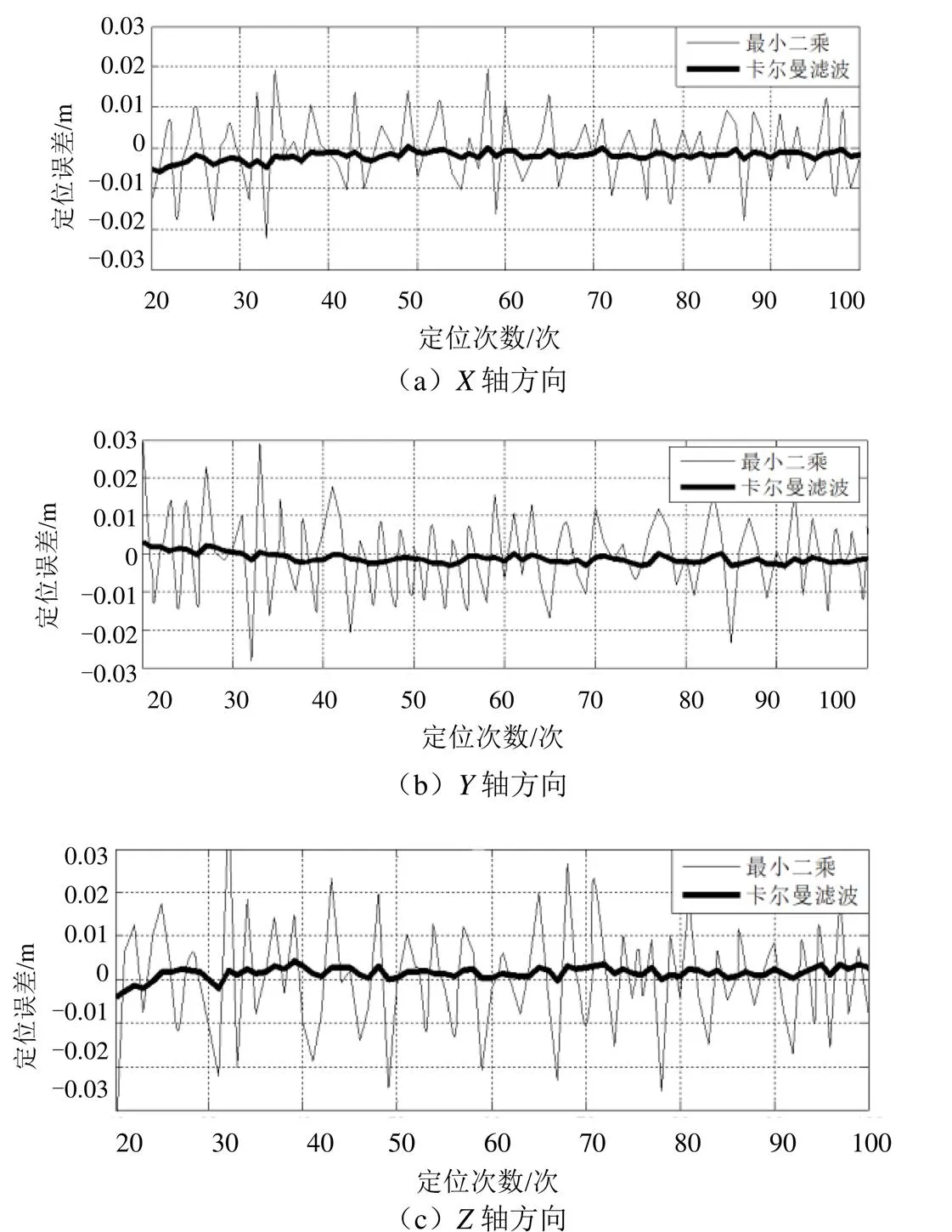
图4 定位结果

表1 最小二乘法定位误差分析（单位：cm）

4 结语

本文设计了一种基于卡尔曼滤波的定位解算方法，通过与最小二乘法定位进行对比试验，结果表明：卡尔曼滤波定位效果优于最小二乘法定位解算，并且相比于最小二乘法每次解算需要至多次迭代的大量运算，卡尔曼滤波算法的计算量也大大降低，只需一次运算就可以得到所需的结果，基于卡尔曼滤波的定位解算算法具有良好的定位效果。

[1] 孙红星，付建红，袁修孝，等．基于多历元递推最小二乘卡尔曼滤波方法的模糊度解算[J]．武汉大学学报：信息科学版，2008（7）：35-39.

[2] 蔡艳辉，程鹏飞，李夕银．用卡尔曼滤波进行GPS动态定位[J]．测绘通报，2006（7）：6-8．

[3] 张勇，田林亚，马丙浩，等．卡尔曼滤波在GPS精密单点定位中的应用研究[J]．测绘通报，2013（7）：8-11．

[4] 李征航，张小红．卫星导航定位新技术及高精度数据处理方法[M]. 武汉：武汉大学出版社，2009．

[5] 施闯，赵齐乐，李敏，等，北斗卫星导航系统的精密定轨与定位研究[J]．中国科学：地球科学，2012，42（6）：854-861.

[6] 宁津生，姚宜斌，张晓红. 全球导航卫星系统发展综述[J]. 导航定位学报，2013.

[7] 刘基余. GPS卫星导航定位原理与方法[M]. 北京：科学出版社，2003.

[8] 谢钢．GPS原理与接收机设计[M]．北京：电子工业出版社，2011．

[9] 倪育德．导航原理与系统[M]．天津：中国民航大学，2012．

[10] 刘基余．GPS卫星导航定位原理与方法[M]．北京：科学出版社，2003．

[11] 许承董，李怀德，张鹏飞，等．GNSS数字仿真原理及系统实现[M]．北京：中国宇航出版社，2014：25-36．

Research on Location and Solution Method Based on Kalman Filter

LIU Mingyang，LI Bin

GPS uses the radio signals transmitted by satellites to determine the position of the user receiver on the earth by calculating the relative position between the satellite and the GPS receiver, and can provide real-time positioning, speed measurement and timing services for the user receiver. The traditional receiver uses the least squares method to solve the positioning, and the coordinates of the receiver are prone to large jumps. By using the principle of Kalman filtering, a model is established according to the motion characteristics of the receiver, and the relationship between the results of each navigation solution is used to smooth the positioning results and eliminate the positioning jitter error caused by the relative independence of the results of the least squares algorithm. The positioning test results show that the positioning algorithm designed in the paper has a good positioning effect.

GPS; Kalman Filter; Analysis of Positioning Results

TN965

A

1674-7976-(2023)-05-353-05

2023-06-06。

刘明阳（1991.10—），河北张家口人，硕士，工程师，主要研究方向为卫星导航应用技术。