Anomalous Hall effect in ferromagnetic LaCo2As2 and ferrimagnetic NdCo2As2

Yu-Qing Huang(黄雨晴), Peng-Yu Zheng(郑鹏宇), Rui Liu(刘瑞),Xi-Tong Xu(许锡童), Zi-Yang Wu(吴紫阳), Chao Dong(董超),Jun-Feng Wang(王俊峰), Zhi-Ping Yin(殷志平), and Shuang Jia(贾爽),5,†

1International Center for Quantum Materials,School of Physics,Peking University,Beijing 100081,China

2Foshan Xianhu Laboratory of the Advanced Energy Science and Technology Guangdong Laboratory,Xianhu Hydrogen Valley,Foshan 528200,China

3Department of Physics and Center for Advanced Quantum Studies,Beijing Normal University,Beijing 100875,China

4Wuhan National High Magnetic Field Center and School of Physics,Huazhong University of Science and Technology,Wuhan 430074,China

5Kunshan Innovation Institute of Nanjing University,Kunshan 215347,China

Keywords: anomalous Hall effect,ferrimagnetism,magnetic compensation,meta-magnetic transitions

1.Introduction

The anomalous Hall effect (AHE), which generally occurs in the conductive ferromagnetic (FM) materials, describes the phenomenon that an electrical current flows perpendicular to an electrical bias due to a non-zero internal magnetization.[1]There has been a chronic debate on whether the AHE is steming from an intrinsic electronic band effect of an unperturbed crystal or from an extrinsic magnetic impurity scattering.[2-5]A remarkable step forward of the theory is the connection between the intrinsic AHE and Berry curvature field in the relativistic band structure of FM materials.[1,6]The development of Berry phase physics breaks the paradigm of the scaling of the AHE with the strength of magnetization.The AHE has been experimentally observed in various antiferromagnetic(AFM)compounds with small or even null net magnetization(MS).[7-9]

Ferrimagnetism (FIM) is a type of long-range magnetic ordering which can be regarded as an AFM with two unequal magnetic sub-lattices.[10]Because of the anti-parallel coupling of the sub-lattice moments, an FIM material generally has smallMSwhich takes complicated dependence on the temperature and external magnetic field.[11,12]As the magnitude and the interaction strength of the sub-lattice moments change at finite temperature, the direction ofMScan reverse when cooling an FIM material from its critical temperature to zero temperature.The most well-known FIM materials are rare-earth-transition-metal(R-TM)alloys in which the R and TM atoms are randomly distributed.Their magnetic moments cancel each other out at the magnetic compensation temperature (Tcomp) and theMSconverges to zero.[13,14]A wide range of fast magnetic dynamic phenomena,including optical switching,[15]current-induced magnetization switching,[16,17]and domain wall motion[18]were observed nearTcompin RTM alloys,which render them as promising candidates for future spintronic devices with higher speed and density.[4,9]In finite external field, the R-TM alloy can undergo a series of meta-magnetic transitions(MMTs),from an FIM in zero field to a spin-flop transition at the critical field ofHsfand finally to a saturated state in which the magnetic moments of R and TM align collinearly.[20,21]The AHE is a reliable signature for detecting the magnetic compensation and the MMTs in the RTM FIM thin films.[22-25]

Unlike in R-TM alloys, the AHE in FIM compounds remains virtually unexplored until recently.First principle calculations predict a nontrivial intrinsic AHE in compensated Heusler ferrimagnets.[26,27]A large intrinsic AHE in FIM RMn6Sn6is stemming from the strong Berry curvature field of Chern-gapped Dirac fermion in Mn-based kagome lattice.[28,29]Here we focus on the AHE and magnetotransport properties of FIM NdCo2As2and FM LaCo2As2.Unlike RMn6Sn6, in which the magnetization of Mn sub-lattice prevails that of R, the magnetizations of Co and Nd sub-lattices are comparable in NdCo2As2.Since the Co and R atoms are periodically distributed in the crystal structure, the magnetic structure of NdCo2As2is much more complicated than that of R-TM alloys.In this work,we find that the AHE is a sensitive signature for identifying the magnetic structure change in this FIM compound.

Crystallized in a ThCr2Si2-type structure, RCo2As2is formed by stacking covalently bonded Co2As2layers with R atoms[30](Fig.1(a)).The magnetic properties of cobaltbased ThCr2Si2-type compounds have delicate relationship with the electron count and crystal structure.[31-33]When the R atom is lanthanum which has no 4f electron, LaCo2As2shows an FM ground state with a Curie temperature ofTC=178 K and the saturated magnetizationMsatbeing 0.59µB/Co atom.[34-37]CeCo2As2is an FM Kondo lattice which exhibits a significantly enhanced intrinsic AHE.[38]When the R atom is neodymium which bears well-defined local moment of the 4f3electronic configuration,NdCo2As2manifests an FIM state in which the magnetic moments of the Co sublattice are anti-parallel to that of the Nd sub-lattice.[33-35]Previous magnetization measurement on the polycrystalline sample of NdCo2As2demonstrated signatures of magnetic compensation and MMTs.[34]However,due to the lack of electrical transport and magnetic properties for the single-crystalline samples, the ground state and the nature of the MMTs in NdCo2As2have not been fully understood.

In order to better understand the AHE in NdCo2As2,we comparably investigated the magnetic and transport properties of single-crystalline LaCo2As2.As a non-4f-electron counterpart, the metallic FM LaCo2As2has purely intrinsic AHE originating from the Berry curvature field,which is consistent with the first principle calculation.In contrast, FIM NdCo2As2displays pronounced sign reversal and multiple hysteresis loops in temperature- and field-dependent magnetization, Hall resistivity (ρyx), and magnetoresistance (MR=(ρ(H)-ρ(0))/ρ(0)).Realizing the contribution from the Co sub-lattice dominates in the AHE for NdCo2As2,we deduced a complicated phase diagram which contains magnetic compensation and multiple MMTs.Our results demonstrate the extreme sensitivity of the Hall effect on the details of the magnetic structures in an FIM compound.

2.Method

Single crystals of RCo2As2were grown from Bi flux as reported in Refs.[34-36,39].However, we found that the remnant bismuth in the sample conducts electric current in the electrical measurement and brings serious misreading of its transport properties.To overcome this issue, we used a self-flux solution-growth technique to grow single crystals of LaCo2As2and NdCo2As2.Precursor CoAs was synthesized by reacting cobalt powder(99.9%,Alfa Aesar)and As lumps(99.9%)in a sealed fused silica ampule at 1170 K for 12 hours.Then lanthanum ingots (99.9%, Alfa Aesar), neodymium ingots(99.9%,Alfa Aesar)and CoAs lumps were packed in an alumina crucible with a molar ratio of 1:3.The crucible was then loaded into a fused silica ampule which was sealed with argon gas at 0.1 atm (1 atm=1.01325×105Pa).The ampule was heated to 1423 K in 10 h and held at this temperature for a week.Several plate-like single crystals with dimensions approximate 0.4 mm×0.5 mm×0.1 mm were separated after centrifugation at 1423 K.The crystal structure was confirmed by powder x-ray diffraction (CuKα) measurements at room temperature in a Rigaku MiniFlex600 diffractometer.

Electrical transport measurements for polished single crystals were carried out in a quantum design physical property measurement system(PPMS-9).The standard four-point method was adopted and silver paste was used as the contacts.The longitudinal resistivity and Hall resistivity measurements were conducted with fields normal to and currents within theabplane.The size of samples was measured using a reading microscope to calculate the electrical resistivities, and the dimension error is estimated at about 10%.A quantum design magnetic property measurement system (MPMS-3) was used to perform the magnetization measurement with the applied field direction being along the crystallographiccaxis on the samples.

We performed density functional theory (DFT) calculations to compute the electronic structure of LaCo2As2in the FM state by using the Viennaab initiosimulation package(VASP).[1]We used the experimental lattice parameters for LaCo2As2.[39]The projected augmented wave method and the generalized gradient approximation (GGA) of Perdew-Burke-Ernzerhof (PBE) were chosen.The plane-wave-basis cut-off energy was set to be 600 eV.As for the topological property, the Berry curvature and anomalous Hall conductivity(AHC)were calculated with the tight-binding(TB)method with Wannier90[41]and WannierTools softwares.[42]

In order to capture the electronic correlation effect,we first performed density functional theory plus dynamical mean-field theory (DFT + DMFT) calculations[43,44]to compute the electronic structure of LaCo2As2in the FM states.The DFT part was calculated by the linearized augmented plane-wave method as implemented in WIEN2k.[45]The PBE exchange-correlation functional was used.We treated Co-3d correlated and HubbardU= 5.0 eV, Hund’s couplingJ=0.8 eV were used, in consistent with the previous calculations.[46]We chose the “exact” double-counting scheme to solve the double counting problem.[47]The impurity problem in DFT+DMFT was solved by using the continuous time quantum Monte Carlo method atT=100 K.[48,49]Then, we renormalized the TB parameters obtained from the DFT calculations to fit the DFT+DMFT calculated band structure around the Fermi level and then shifted the Fermi level before plotting the band structure and computing the topological property.

3.Results

As shown in Fig.1, the magnetic properties of the LaCo2As2crystals grown from CoAs flux are identical to those from Bi flux.[34-36,39]Temperature-dependent magnetization (M(T)) in an applied fieldµ0H=0.1 T shows an FM state with an easy-c-axis andTCof around 170 K.The soft FM state is verified by isothermals of magnetization belowTC(Fig.1(c)),which shows anMsatbeing 1.1µBper formula unit(f.u.)at 2 K.Temperature dependence of resistivity(ρ(T))has a profile of a metal with a significant slope change atTC,most likely due to loss of spin-disorder scattering in the FM state.

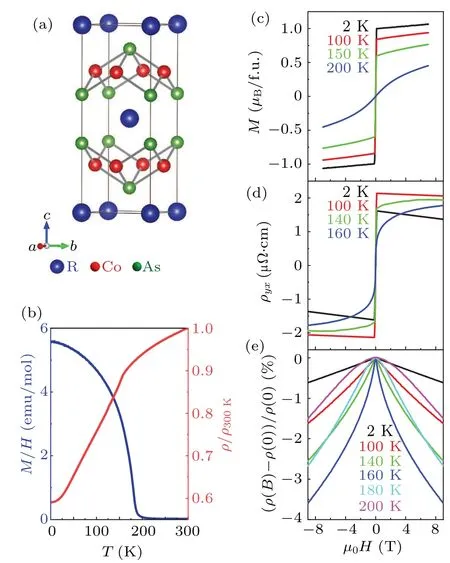
Fig.1.Magnetic properties of LaCo2As2.(a) Unit cell of RCo2As2.(b)Temperature dependence of the magnetization(blue)in an external magnetic field of 0.1 T along the crystallographic c axis, and normalized zerofield longitudinal electrical resistivity ρ/ρ300 K(red).(c)-(e)Magnetization,Hall resistivity,and MR with respect to the applied field along the direction of c axis at representative temperatures,respectively.

Isothermals ofρyx(H)and MR with respect to the applied field are shown in Figs.1(d) and 1(e), respectively.Negative MR is commonly observed in FM metals due to suppression of the spin-disorder scattering by an external field.Theρyx(H)approximately follows the magnetic isothermals, revealing a pronounced spontaneous AHE.Empirically,ρyxof an FM material comprises two terms[1]

whererepresents the ordinary Hall resistivity,the anomalous Hall resistivity,R0the ordinary andRSthe anomalous Hall coefficient.Fitting the data at 2 K, we obtainedR0being-2.8×10-4cm3/C andRSbeing 4.4×10-5cm3/C,leading ton=-2.30×1022cm-3, a typical electron density for an n-type metal.

Next, we demonstrate the magnetic and electrical transport properties of the single crystals of NdCo2As2.ItsM(T)has a typical profile of an FIM which hasTCaround 90 K andTcomparound 10 K(Fig.2(a)).Because the Co sub-lattice orders ferromagnetically alongcaxis at first,Mhas an abrupt increase when temperature is belowTC.The moments of Nd atoms are gradually ordered under the influence of the internal field induced by the Co sub-lattice.Because the Co and Nd magnetic moments intend to align in anti-parallel,MSstarts to drop below 33 K.The contributions from the two sub-lattices become nearly equal at about 10 K which is theTcompfor NdCo2As2, very close to the literature report.[34,35]At lower temperature theM(T)abruptly increases.

Fig.2.Magnetic properties of NdCo2As2.(a) M/H (blue) in an external magnetic field of 0.1 T, and ρ/ρ300 K in zero field.(b)-(d) Magnetic isothermal loops of NdCo2As2 (blue) and LaCo2As2 (red) in the applied field parallel to the direction of c axis at 50 K, 7 K, and 2 K, respectively.(e) High-field magnetization of NdCo2As2 at 2 K.Inset: M (blue) and ρyx(red) in low field at 2 K.Please note there are additional small hysteresis loops in M(H)and ρyx(H)at 2 K(inset in Fig.2(e)),indicating a noncolinear magnetic texture in zero field at base temperature.

We comparably show the magnetic isothermal loops for FM LaCo2As2and FIM NdCo2As2at three representative temperatures: 50 K, 7 K, and 2 K, in Figs.2(b)-2(d).The magnetic isotherms for LaCo2As2have a typical profile of soft FM which has a coercive field less than 0.1 T and a nearly invariantMsat1.1µB/f.u.As comparison, theM(H)curve for NdCo2As2at 50 K exhibits a spontaneous magnetization (M0T) of 0.25µB/f.u.and then gradually increases in the external field.This observation unveils that the FM Co sub-lattice in NdCo2As2has much lowerM0Tthan that in LaCo2As2.The gradual increase ofM(H) comes from a convergent effect of alignment of the Nd moments and polarization of the Co moments.When temperature decreases,the Nd moments grow up and cancel out the magnetization of Co moments, which results in a drop of theMSin zero field.At 7 K, a small hysteresis loop is visible in low field.At 2 K,M0Tturns back to the similar magnitude as at 50 K while an MMT occurs at 3 T.

We measured a piece of single-crystalline NdCo2As2at 2 K in pulsed field in Wuhan National High Magnetic Field Laboratory in China and the result was shown in Fig.2(e).Besides the MMT at 3 T, there is another MMT at 10 T and then the magnetization intends to saturate at higher field.The value of magnetization reaches 2.5µB/f.u.at 10 T and then grows up to 3.2µB/f.u.at 25 T which is still slightly less than the expectedMsatof the collinearly parallel Co moments 1µB/2Co plus Nd moment of the Hund’s rule ground state(3.2µB/Nd3+).

To shed a light on the magnetic structural changes in NdCo2As2,we demonstrate theM(H)and its derivation to the field (dM/dH),ρyx(H), and MR isothermals at representative temperatures in Fig.3.To better describe the magnetic structural changes, we divide the temperatures belowTCinto several regions in which theM(H),ρyx(H),and MR show different behaviors.An AHE is visible with a spontaneous Hall resistivity (ρyx,0T) below 80 K.From 80 K to about 30 K,M0Tandρyx,0Tgradually increase with decreasing temperature and there is no evident hysteresis loop.The MR remains negative in the whole field range above 50 K but starts to turn up in high field at 30 K.The negative MR,M0T, and AHE with no visible hysteresis are similar as those in the FM state for LaCo2As2, but the magnitudes ofM0T,ρyx,0T, and MR are relatively smaller.

Fig.3.Magnetic isothermals for NdCo2As2.(a)Magnetization,(b)derivative of the magnetization dM/dH,(c)Hall resistivities,and(d)MR at different temperatures in the applied field oriented parallel to the c axis.The current was applied along the a axis for transport measurements.The loops are shifted vertically upward with random offsets.

From 30 K to 10 K, pronounced hysteresis loops occur near zero field inM(H) andρyx(H) isothermals.While the coercive fields of the hysteresis loops inM(H) andρyx(H)grow up with decreasing temperature and become the greatest at 10 K,M0Tcontinuously drops in this region.On the other hand,ρyx,0Tslightly increases from 30 K to 10 K.The MR curves change to positive and exhibit a butterfly-shaped feature near zero field due to the domain wall motion.[50]

NearTcomp, it is difficult to identify the hysteresis loop and MMT inM(H)curves.However we can identify a series of subtle magnetic structure changes by scrutinizingρyx(H)and MR curves.Striking and abrupt changes occur from 10 K to 9 K and then from 7 K to 6 K inρyx(H) curves.At 9 K,ρyx,0Tchanges the sign(please note the arrows which indicate the field sweeping direction), and thenρyx(H) switches back at±7 T with the same amplitude as at zero field.The critical field of this MMT drifts to±10 T at 2 K which is visible in theM(H)curve in Fig.2(e),but nearTcompthe corresponding change of magnetization is invisible.

The phenomenon of sign reversal in theρyx,0TnearTcompis commonly observed in the R-TM alloy thin-films.[18,22-24]However for NdCo2As2the reversed hysteresis loops ofρyx(H) occur only in a very narrow temperature range from 9 K to 7 K.At 7 K a peculiar feature is visible at±1 T in the loop ofρyx(H).At 6 K the loop collapses to an MMT at±3 T whileρyx,0Tswitches back to positive.From 6 K to 2 K the profiles ofρyx(H) remain unchanged in principle.Yet a tiny loop ofρyx(H)andM(H)occurs near zero field at 2 K which is highlighted in the inset of Fig.2(e).

Unlike the dramatic changes ofρyx(H),M(H) isothermals are almost identical from 10 K to 7 K.Below 7 K a pronouncedM0Treoccurs and an MMT occurs at about±3 T with large hysteresis.These features are more visible in the dM/dHcurves.

Below 10 K,the MR changes in a similar manner as the dM/dHcurves.NearTcomp, the weak butterfly-shaped features near zero field are almost identical.The MR curve shows a knee point at the MMT about±7 T and in higher field it changes to negative.At the other MMT about±3 T below 7 K,there is a pronounced jump of MR with large hysteresis.

To better demonstrate the magnetic compensation of NdCo2As2, we plot temperature dependence of the coercive field,M0Tandρyx,0.5Tbelow 20 K in Figs.4(a)and 4(b).The coercive field of the loops inρyx(H) andM(H) is maximum at 10 K while theMSconverges to zero.It is a general feature because the FIM requires a larger external magnetic field to obtain a sufficiently high Zeeman energy to switch the magnetization nearTcomp.[23]On the other hand,ρyx,0.5Tswitches the sign when the temperature drops from 10 K to 9 K and then re-switches below 7 K.It is worth noting that the sign re-switch of the AHE has never been observed in R-TM FIM alloys.This indicates that NdCo2As2undergoes an additional magnetic structure change rather than a simple magnetic pole reversal belowTcompas in R-TM alloys.[20,21]

We plot the temperature dependence of the values ofρyx(H)in up and down sweeping fields in Figs.4(c)and 4(d),respectively.When the magnetic field is less than 1 T,ρyxswitches the sign from 10 K to 9 K and then re-switches from 7 K to 6 K.We notice the values ofρyxbelow 6 K fall into the same line as that above 10 K,which indicates similarity in the magnetic structures.The sign re-switch vanishes in 3 T of up sweeping field and 2 T of down sweeping field,corresponding to the MMT at±3 T with large hysteresis.In higher field the value ofρyxat base temperature increases with the field.The two MMTs and the re-switch ofρyxindicate that NdCo2As2has at least three different magnetic structures in various temperatures and fields.

Fig.4.Signature of the compensation point in NdCo2As2.(a)and(b)Temperature dependence of the width and the magnitude of the loops in M(H)and ρyx(H) near zero field, respectively.(c) and (d) Temperature dependence of the ρyx in different magnetic fields when the field sweeps up (+)and down(-),respectively.

4.Analysis and discussion

Now we analyze the AHE in LaCo2As2and NdCo2As2and clarify their mechanisms, for the sake of understanding their magnetic structures.For a spontaneous Hall effect,AHC(σAH)is obtained from the relation

To clarify the relationship between the AHE and Berry curvature field in LaCo2As2,we preformed first principle calculations to compute the electronic structure and topological property.The renormalized DFT band structure of LaCo2As2in the FM state is shown in Fig.6,which is in good agreement with the ARPES results.[38]The bands mainly from Co-3d contribution intersect with each other and form nodes around the Fermi level.Due to the large Fermi velocity of the delectron bands, the corresponding Berry curvature is small,and the positive and negative contributions of them mostly offset each other.The low Berry curvature density results in low AHE, as shown in Fig.6(c), which can naturally explain the intrinsic AHE of the experimental results.

We now try to understand the spontanous Hall effect of NdCo2As2in the temperature range from 10 K to 50 K.As shown in Fig.5(b), bothandσAHare strongly enhanced when temperature drops.We notice that theρxx(T) changes less than 10%from 50 K to 10 K whereasM0Tchanges from 0.20µB/f.u.at 50 K to the maximum value of 0.24µB/f.u.at 33 K and then to a very small value of 0.03µB/f.u.at 7 K.Obviously, the change ofσAHandhas no explicit functional relation with the change ofρxx(T)or magnetization either.The failure of the scaling law for NdCo2As2is confirmed in Fig.5(d), which indicates that the AHE is not determined byMSof the anti-parallel Co and Nd sub-lattices.

The sign switch of the spontanous Hall effect nearTcompin NdCo2As2indicates that the AHE is stemming from the Co sub-lattice although the electronic structure and Berry curvature field will be different from that of LaCo2As2.Because the AHE is extremely sensitive to the magnetic structure change,we can infer the nature of the magnetic compensation and MMTs and build up a phase diagram for NdCo2As2, similar to the R-TM alloys.[18,23-25]

In order to better demonstrate the change ofρyxin the MMTs,we subtract the value at 15 K as the linear background(Δρyx=ρyx-ρyx,15K).The contour maps in the plane of temperature and magnetic field are shown in Figs.7(a) and 7(b)in which the field swept up and down,respectively.It is noteworthy that the value of Δρyxat low temperature in zero field is close to that at high temperature and field, which indicates that the magnetizations of the Co sub-lattice are same in the two regions.The sign reversal of the AHE occurs in the middle region in which the direction of the Co magnetization is anti-parallel to the external field.

Such complicated magnetic structural changes are not anticipated in the R-TM alloys which typically go through only one spin-flop transition inHsf.[20,21]In the R-TM alloys, the anti-parallel magnetic moments of R and TM get canted and form a noncollinear structure in a magnetic field.After going through the spin-flop transition, the canting angle is further controlled by the increasing magnetic field higher thanHsfuntil both moments align collinearly along the strong saturation field.However in RCo2As2the relatively weak RKKY interaction between the local moments of R3+ions may give rise to an AFM ordering of the R sub-lattice.We compare the magnetic structural changes of PrCo2As2which have been identified by the neutron diffraction experiment.[35]While theTCfor the Co sub-lattice is 140 K,the Pr moments start to order at 25 K,anti-parallel to the Co moments.At base temperature the Pr atoms form two sets of nonequivalent magnetic sub-lattices in zero external field due to the magnetic interaction between the Pr moments.We believe similar magnetic structure exists in NdCo2As2at base temperature.Noticing thatM0Tandat 2 K are identical to that above 10 K,we infer that the Nd sub-lattice forms an AFM texture while the Co sub-lattice aligns FM and contributesM0Tandsolely in region I in the phase diagram(Fig.7(c)).Magnetization of Nd moments no longer cancel out that of Co moments,resulting in a sharp increase ofM(T) curve at low temperature in Fig.2(a).The MMT at±3 T corresponds to a spin flop transition in which half of the Nd moments switch the direction along with the external field, which leads to a reversal of the magnetization of the Co sub-lattice.The second MMT at high field is a spinflop transition(Hsf)above which the magnetization of the Co sub-lattice re-switches,similar as the R-TM alloys.[20,21]

Fig.7.(a)and(b)Contour maps in the plane of temperature and magnetic field for Hall resistivities in NdCo2As2 with(a)up and(b)down field sweep.The color bars at the side of the maps represent the Hall resistivities after subtracting the value at 15 K, Δρyx =ρyx-ρyx,15 K.(c) Phase diagram of NdCo2As2.Arrows visualize the orientations of Co(red)and Nd moments(blue).The inset shows the contour map in the plane of temperature and magnetic field for the magnitude of magnetization.

The observed change of MR in the MMTs can be interpreted by the inferred magnetic phase diagram.At low temperature, the MMT in low field is assigned to the reverse of half of large Nd-4f-electron moments, which causes significant changes in theMSand electron scattering.Correspondingly,we observed a dramatic change with large hysteresis in theM(H)and MR curves.As comparisons,the MMT at high field is only assigned to the reverse of small Co-d-electron moments,resulting in a much smaller change in electron scattering.In the above discussion we ignore the small hysteresis loops inM(H)andρyx(H)at 2 K(inset in Fig.2(e)),which indicates an additional noncolinear magnetic texture in zero field at base temperature.Future studies, such as neutron diffraction, will help to unveil the details of the magnetic structures in NdCo2As2.

5.Conclusion

In summary, we have studied the magnetic and transport properties in response to the complex magnetic structures of FIM NdCo2As2and FM LaCo2As2as comparisons.Unlike the purely intrinsic mechanism in LaCo2As2, the AHE in NdCo2As2is sensitive to the multiple phase transitions induced by the competing interaction between Nd an Co sublattices especially near the magnetic compensation point.Understanding the relationship between the magnetic structural change and AHE will help to explore the complicated phase diagram of FIM compounds, which may lead to a promising platform for future spintronic devices with higher speed and density.

Acknowledgements

The authors thank Jia Li, Wei Han for the fruitful discussions.Project supported by the National Key Research and Development Program of China (Grant No.2018YFB1502502), the National Natural Science Foundation of China (Grant Nos.12141002 and 12225401), the Fund from Foshan Xianhu Laboratory of the Advanced Energy Science and Technology Guangdong Laboratory.The work in the high magnetic field lad was supported by the Interdisciplinary Program of Wuhan National High Magnetic Field Center (Grant No.WHMFC202123), Huazhong University of Science and Technology.Z.Y.was supported by the National Natural Science Foundation of China (Grant Nos.12074041 and 11674030),the Foundation of the National Key Laboratory of Shock Wave and Detonation Physics(Grant No.6142A03191005),the National Key Research and Development Program of China(Grant No.2016YFA0302300),and the startup funding of Beijing Normal University.The calculations were carried out with high performance computing clusters of Beijing Normal University in Zhuhai.