基于红外锁相法缺陷深度检测的仿真

牛 奕，吴 锡，甘玲童，周德闯

基于红外锁相法缺陷深度检测的仿真

牛 奕1，吴 锡1，甘玲童1，周德闯2

（1. 武汉理工大学 安全科学与应急管理学院，湖北 武汉 430070；2. 中国科学技术大学 火灾科学国家重点实验室，安徽 合肥 230026）

隐藏在工件内部的粘贴结构缺陷具有隐蔽性和危险性，成为影响生产质量和运行安全的致命因素，运用红外无损检测技术可以对其缺陷进行检测和评估。本文通过仿真模拟，测得粘贴结构在不同缺陷深度以及涂层热扩散系数下的盲频率，研究了缺陷深度和涂层热扩散系数对盲频率的影响，同时利用拟合定量研究了盲频率与缺陷深度和涂层热扩散系数的关系。仿真结果表明，可以通过盲频率求得热扩散长度，进而求得缺陷深度的定量检测方法。

红外无损检测；粘贴缺陷；缺陷深度检测；红外锁相

0 引言

粘贴结构在建筑施工、工业制造、日常生活等方面应用广泛，并具有优越性。但由于粘贴结构受到生产工艺、环境因素等情况影响，不可避免地存在着缺陷。大多数粘贴结构使用中的故障是由粘合表面和粘合剂之间界面的脱粘引起的[1]。为防止因粘贴结构的内部缺陷引发安全事故，需要一种无损检测技术对粘贴结构是否存在缺陷进行检测。红外无损检测法对比传统无损检测法具有周期短，范围广、面积大、效率高、结果可视性等特点[2]。红外无损技术根据不同激励方式，分为持续激励法、脉冲激励法以及锁相激励法[3]。运用红外无损技术观测时序热像图中存在直流分量、噪声信号等干扰信号。相比于持续和脉冲激励法，锁相激励法的优点是将微弱信号从干扰信号中分辨出来[4]。同时，锁相激励法受到加热不均匀的影响较小，检测过程中所需要的能量相对较低，信噪比高等优势[5]。基于上述优点，本文采用红外锁相法展开研究。

许多学者基于红外锁相法对缺陷进行实验和仿真模拟。W. Bai等提出的光热模型可用于预测盲频率，并且得出盲频率随着缺陷的深度而变化，缺陷越深，盲频越小[6]。唐庆菊等制作不同深度缺陷的试件，讨论幅差、相位差、信噪比与调制频率的关系，建立自适应神经模糊推理系统模型，预测缺陷深度[7]。张金玉等建立涂层三维非稳态导热模型，对模型的正弦调制加热过程进行模拟，分析相位差与涂层厚度、缺陷尺寸的关系[8]。刘俊岩等采用有限差分法并建立热-电等效模型，得到缺陷深度和反射热波与入射热波相位差的关系，获得缺陷大小和位置[9]。陈林等利用有限体积法并建立二维瞬态导热模型，得到相位差与调制频率、缺陷的深度、宽度、高度以及材料的关系[10]。田裕鹏和杨如意对缺陷深度和面积大小的红外定量检测问题进行实验和有限元模拟计算研究[11-12]。沈剑峰等运用一维热传导模型，获得表面温度与缺陷深度调制频率的关系，通过调制频率，确定热扩散长度，检测缺陷深度范围[13]。此外，还有学者基于PSO-BP神经网络[14]和小波变换[15]等的红外无损检测对缺陷进行检测和识别。然而在红外锁相法研究中，多数被简化为一维热传导模型进行分析，但实际情况，多数传热不能简化为一维，故需要研究多维热传导情况。

本文主要基于红外锁相法对粘贴结构缺陷进行定性定量分析。研究缺陷深度和涂层热扩散系数对盲频率的影响，确定了盲频率计算缺陷深度的方法，实现对缺陷深度的定量检测，提供了技术基础和理论依据。

1 锁相法检测缺陷深度原理

1.1 红外锁相法检测缺陷原理

红外锁相法是使用周期性的热源对试样进行外部激励，而试样内部的缺陷处和非缺陷处会有不同的周期性的响应，进而引发温度场的变化，造成相位的不同。然后运用数字锁相技术提取和记录试样的表面温度，得到对应的相位图，分析相位图和幅值图得到试样缺陷尺寸和缺陷深度等信息。红外锁相法的原理如图1所示。

1.2 缺陷深度检测原理

如图2所示，当缺陷和非缺陷区域没有相位差或者相位差非常小，在此频率下不能检测到缺陷，此时的频率称为盲频率。因为盲频率受涂层热扩散长度的影响，且热扩散长度与缺陷深度存在正比关系，所以在测得盲频率的条件下，得到热扩散长度，然后用热扩散长度计算缺陷深度，最终实现定量化检测缺陷深度。

若已知涂层热扩散系数，盲频率与缺陷深度的关系可表示为：

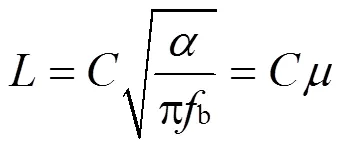
式中：为缺陷深度；b为缺陷深度为时的盲频率；为热扩散长度；为相关系数；为热扩散系数，等于/；其中为导热系数、为密度、为比热容。

2 多层热传导模型一维分析

W. Bai[6]提出的对流条件下有限厚度的多层介质的一维热波传导模型，使用热传导模型可得到正弦调制热波激励下试件的纵向温度分布，通过表面温度情况可计算得到表面相位角。

在每一层中，温度分布服从公式(2)：

式中：Ti为介质i层内的温度。

对于试件的前表面，主要考虑受到正弦变化的热流和与空气的对流，其边界条件可表示为：

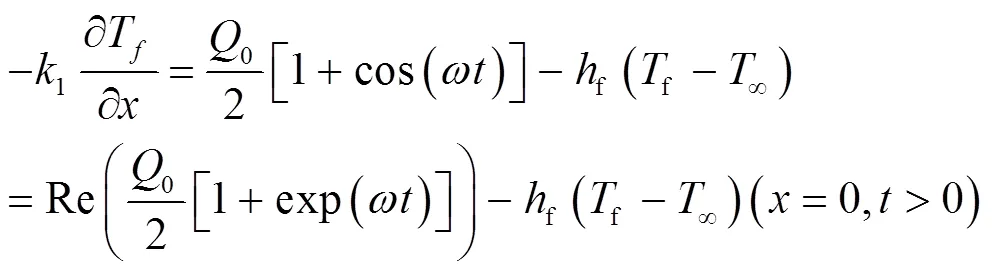
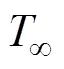
对于试件的后表面，主要考虑受到与空气的对流作用，其边界条件可表示为：

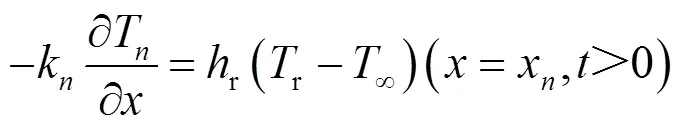
当温度达到稳定状态时，多层模型中每层温度分布由直流和交流分量组成，其表达式为：

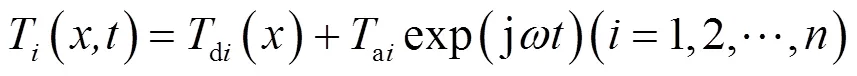
式中：di()为第层温度分布的直流分量；ai()exp(j)为第层温度分布的交流分量。

由于温度的直流分量不随时间的变化而变化，相位差的产生依赖于交流分量，因此主要考虑交流分量。故可得到：

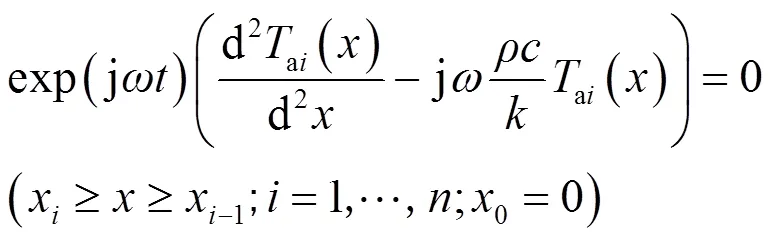
对应的边界条件为：

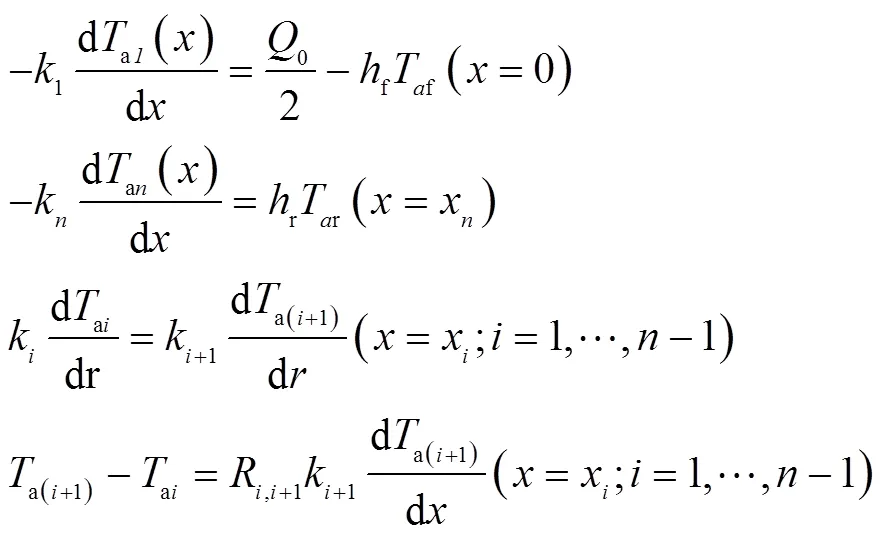
式中：r为介质下表面的换热系数；R,i+1为两层介质之间的接触热阻。

交流温度分量的一般解可写为：

试件表面的反射波与入射波之间的相位角为：

＝Arg(1＋1) (9)

有缺陷的试件可以近似看作为多层一维结构，其中间层是粘合剂，但粘合剂内部存在脱粘缺陷。用公式(9)可以计算出相应的相位角defect，normal。有缺陷和无缺陷区域的相位差为：

D＝normal－defect(10)

W. Bai提出的模型考虑到热对流对表面相位变化的影响，提高了大型平板的计算精度，特别适用于层状或近似层状的缺陷结构，其它缺陷结构使用时虽会有一定误差，但仍有一定的参考价值。

3 建立模型

W. Bai[6]通过建立对流条件下，有限厚度均匀板的单层和多层介质的一维热传导模型，并利用该热传导模型探究和预测研究样品表面缺陷产生的盲频率。在一维热传导模型里，试件设置为均匀无限大并且有一定厚度的平板。对于试件内部的热传导，只考虑纵向热传导，未考虑横向热扩散对盲频率的影响。为了研究实际过程中横向热扩散对盲频率的影响，建立如图4所示的二维模型。其中激励热源为200W/m2，环境温度为300K，自然对流为2～25W/(m2∙K)，对流换热系数取15W/(m2∙K)，并使用加载方波进行激励。在热源激励下，物体表面温度升高，由于空气的导热系数比胶水的导热系数小得多，导致热量积聚在缺陷区域，所以缺陷位置的温度要高于非缺陷区域温度。缺陷是含有气泡造成的，因此可假设缺陷为空气。

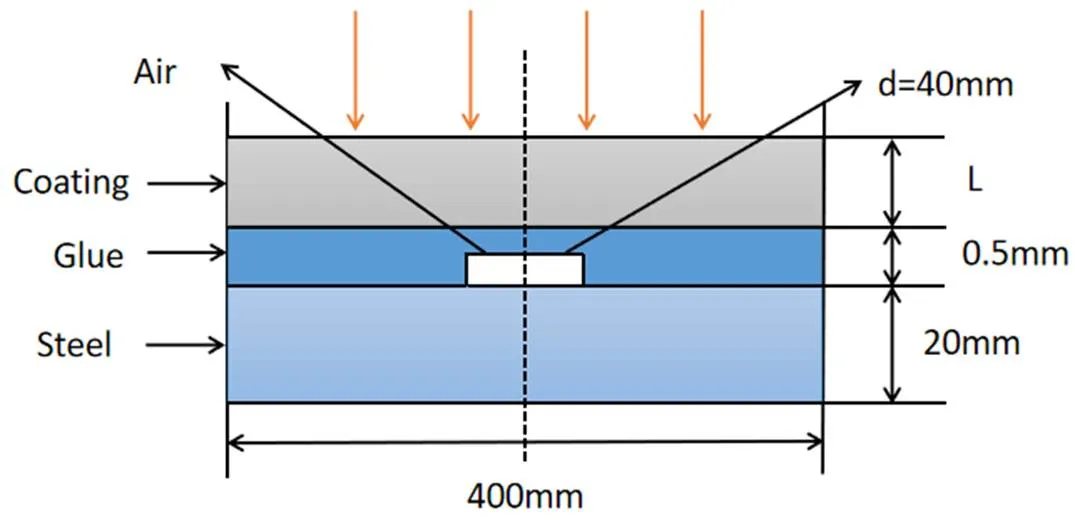
图4 含有粘贴缺陷的二维模型示意图

利用CFD流体分析软件，建立如图5所示的粘贴缺陷二维轴对称模型。在涂层表面分别设置监测点1和2，分别用来提取缺陷区域和非缺陷区域的温度场数据。

假设基体材料使用钢，其厚度为20mm；涂层与基体之间使用胶水（主要成分是聚乙烯醇）粘贴，胶水的厚度为0.5mm，几种材料的热物理特性[16]，如表1所示。

为研究缺陷深度、涂层热扩散系数对盲频率的影响，本文中二维模拟缺陷深度与涂层热扩散系数设置表2所示的计算工况，缺陷深度分别设置3mm，…，10mm等8组数据；涂层热扩散系数分别取5×10-7m2/s，…，5×10-5m2/s等5组数据。缺陷深度与涂层热扩散系数两两组合，共计40个计算工况。

以热扩散系数5×10-7m2/s，缺陷深度6mm，加载频率0.001Hz为例。如图6所示，可以看出缺陷区域有热量聚集的现象。如图7所示，分别提取达到稳态阶段后的2～5个周期的温度场数据，利用快速傅里叶变换计算在频率为0.001Hz时缺陷区域和无缺陷区域的相位角。

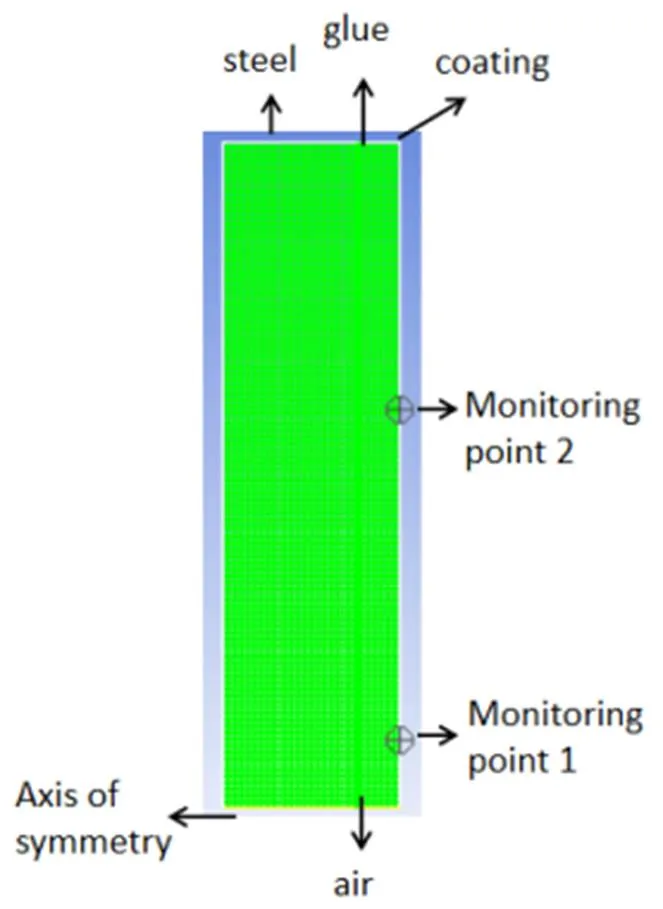
图5 粘贴缺陷的二维轴对称模型示意图

表1 材料热物性参数

表2 缺陷深度与涂层热扩散系数的计算工况

图6 二维仿真模拟计算结果

图7 缺陷区域和无缺陷区域表面温度随时间的变化

4 仿真模拟结果及分析

4.1 缺陷深度对盲频率的影响

利用W. Bai创建的一维无限大的热传导模型可以计算出粘贴结构不同缺陷深度条件下的盲频率。如图8所示，在同一涂层热扩散系数工况中，盲频率随着缺陷深度的增加不断减小，较小缺陷相较于较大缺陷对盲频率的影响也较大；同一缺陷深度工况中，热扩散系数越大，盲频率越大。并且盲频率的斜率也随着缺陷深度的增加不断减小，最终盲频率和盲频率的斜率随着缺陷深度的增加而不断趋近于零，盲频率与缺陷深度存在负指数幂函数关系。

对粘贴结构模型进行二维模拟，可以得出不同缺陷深度下的盲频率。如图9所示，与图8理论分析得到的盲频率折线走向趋势基本一致。理论分析与二维模拟进行对比，结果显示：缺陷深度较小时，模拟和理论分析的误差相对较大，而缺陷深度较大时，模拟和理论分析的误差相对较小。

图9 理论分析和仿真模拟不同缺陷深度的盲频率对比

对于理论分析与二维仿真模拟不同的缺陷深度条件下的盲频率对比的误差，主要是因为：①理论分析没有考虑缺陷尺寸和形状对盲频率的影响，而仿真模拟中，缺陷尺寸和形状对盲频率存在一定程度的影响；②当缺陷面积不变时，缺陷深度越大，缺陷周围的热波横向扩散较高，导致热波衰减较快。③缺陷深度较小时，检测频率范围较大，盲频率较难检测，缺陷深度较大时，检测频率范围较小，盲频率较容易检测。

4.2 涂层热扩散系数对盲频率的影响

利用W. Bai创建的一维无限大的热传导模型可以计算出粘贴结构不同涂层热扩散系数条件下的盲频率。如图10所示，在同一缺陷深度工况中，盲频率随着热扩散系数的增加而不断增加；同一热扩散系数工况中，缺陷深度越大，盲频率越小。并且盲频率和涂层热扩散系数呈线性增加的趋势，即盲频率与涂层热扩散系数存在线性关系。

对粘贴结构二维粘贴结构模型进行二维模拟，可以得出不同涂层热扩散系数条件下的盲频率。如图11所示盲频率增长趋势与图10理论分析基本相同。理论分析与二维模拟进行对比，结果显示：在低热扩散系数时，二维模拟与理论分析的误差相对较小，而在高热扩散系数时，二维模拟与理论分析的误差相对较大，但二维模拟的结果与理论分析的趋势基本保持一致。

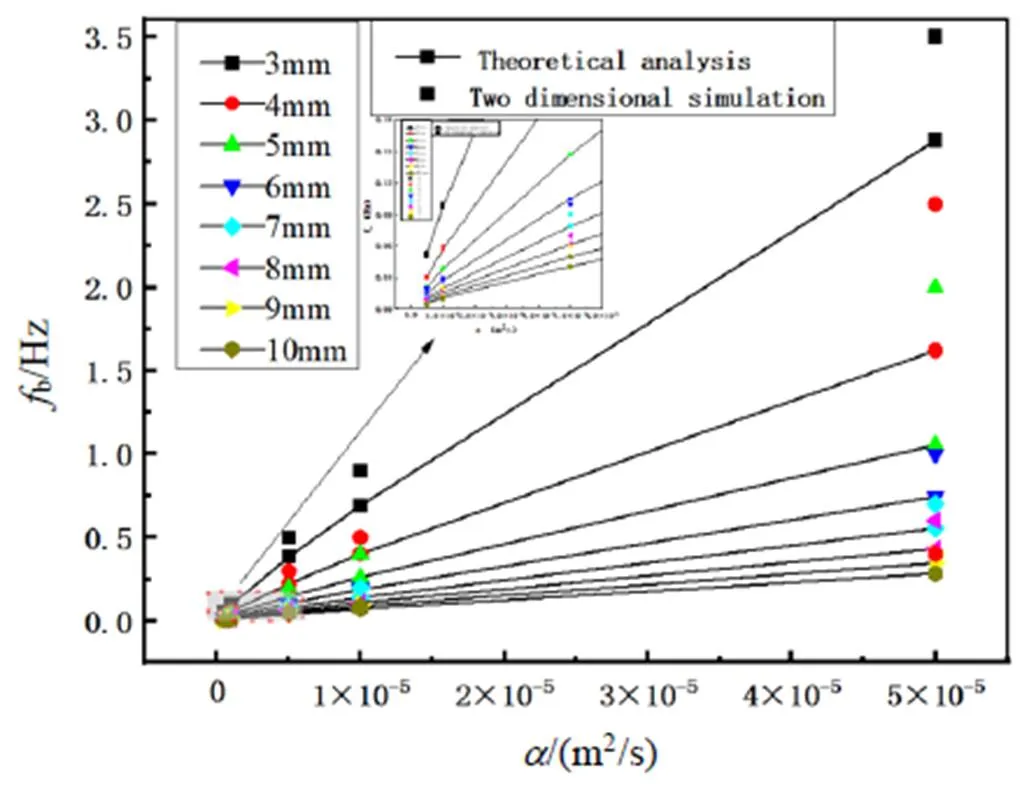
图11 理论分析和仿真模拟不同的涂层热扩散系数的盲频率对比

对于理论分析与二维仿真模拟不同涂层热扩散系数条件下盲频率对比的误差，主要是因为：①理论分析为一维，未考虑横向热扩散，但实际上，激励热波传播遵循三维热波。②受横向热扩撒的影响导致加热周期减小，检测频率增大。③二维模拟中，高频情况下每个周期加热事件较短，试件表面温度变化快，计算步长对结果的影响相对低频时较大。

4.3 基于盲频对缺陷深度的定量预测

运用红外锁相法获得粘贴试件的盲频率，当缺陷深度未知时，由公式(1)可知，缺陷深度与涂层热扩散系数和盲频率之比的平方根存在线性关系。如图12所示，在同一涂层热扩散系数工况中，缺陷深度与热扩散长度呈线性关系，其斜率大小受涂层热扩散长度与缺陷深度共同的影响。

图12 缺陷深度与热扩散长度的关系

为了进一步研究影响缺陷深度与热扩散长度之间系数大小的因素，设置了同样的工况。如图13(a)所示，在同一缺陷深度工况中，/比值与热扩散系数成反比关系，与缺陷深度成正比关系。因为保温材料一般被用做涂层，而保温材料的热扩散系数一般为10－6～10－8，如图13(b)所示，/比值应在1.5～2区间内。

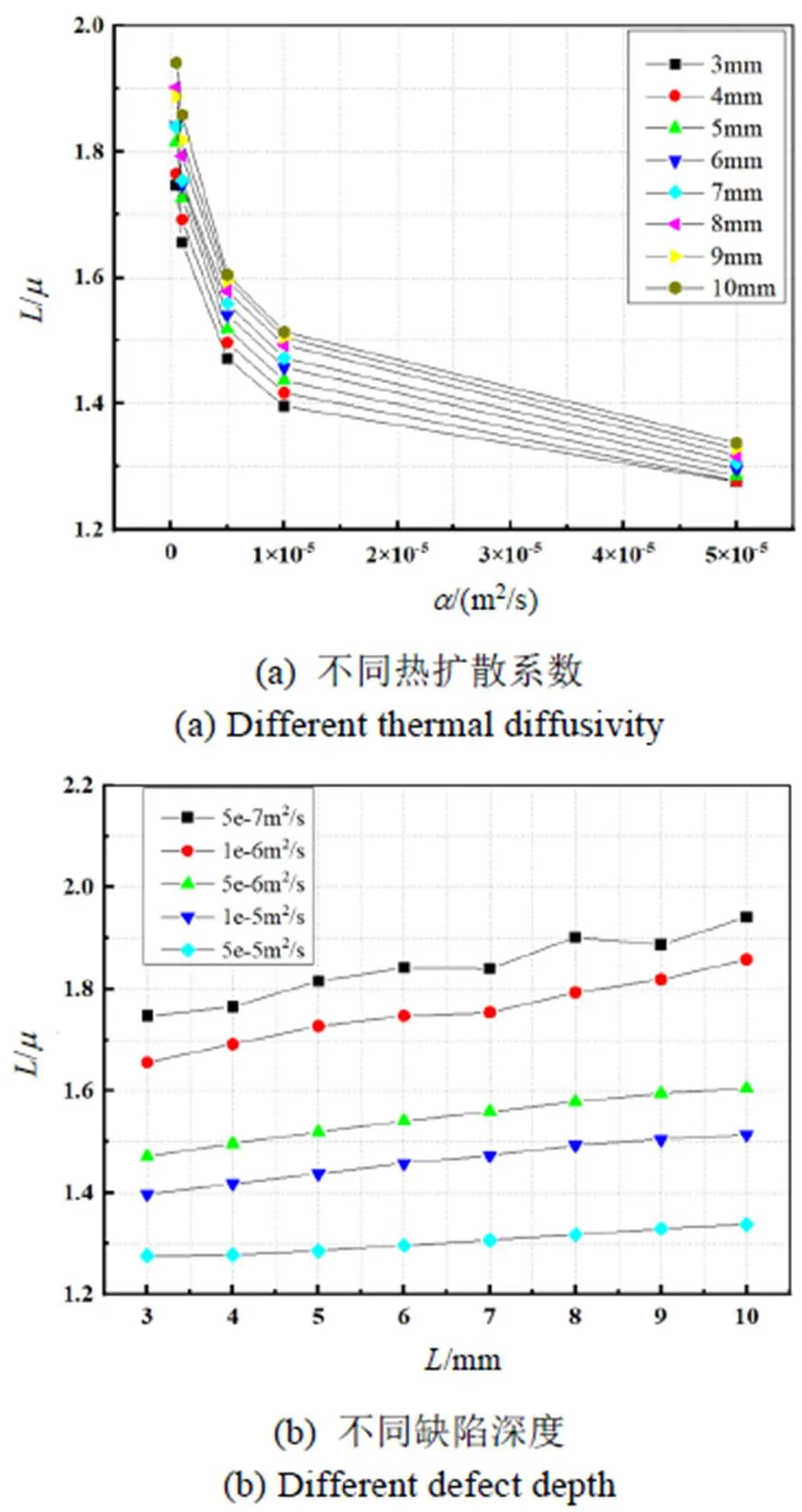
图13 不同工况下的缺陷深度与热扩散长度的比值

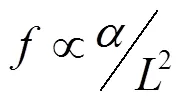
由图14可看出，理论分析和仿真模拟的盲频与涂层热扩散系数和缺陷深度平方之比呈线性关系，经回归分析得到理论分析1＝1.65，二维模拟2＝1.70，所以可基于盲频对缺陷深度进行定量预测。

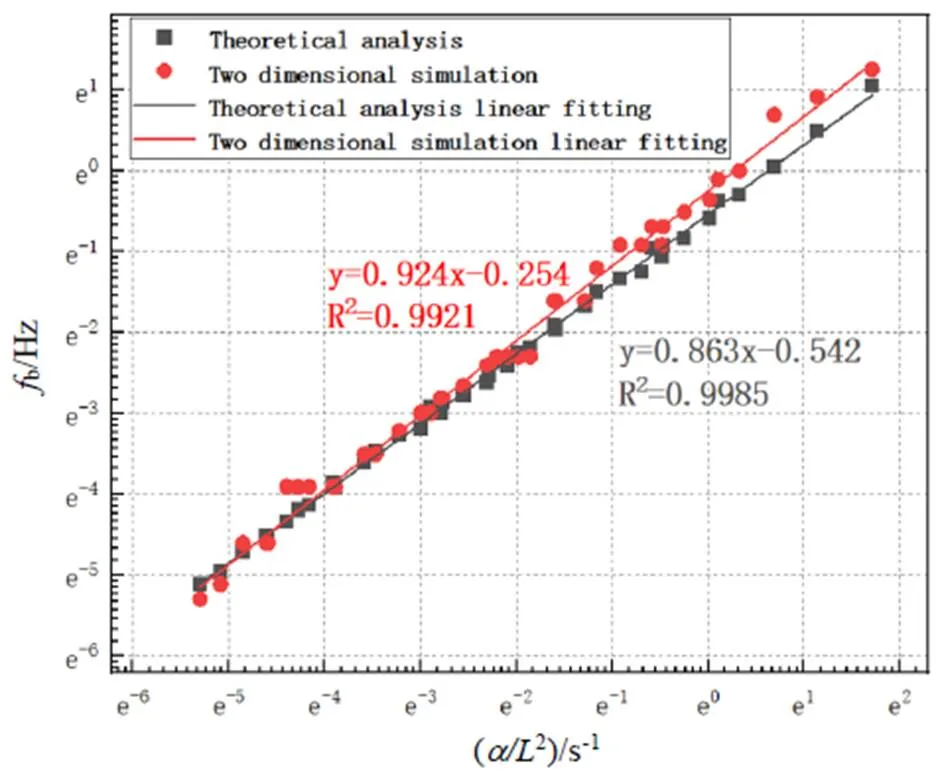
图14 盲频率与涂层热扩散系数和缺陷深度的平方之比拟合

5 结论

本文基于红外锁相法实现对粘贴缺陷的仿真模拟，分析了缺陷深度和涂层热扩散系数对盲频率的影响，提出确定缺陷深度的方法。主要的结论如下：

1）对粘贴缺陷进行定量分析，盲频率与缺陷深度以及涂层热扩散系数可做拟合关系，并且该拟合关系可通过预测的盲频率对试件加热检验涂层厚度。

2）缺陷深度与热扩散长度呈正比关系，其斜率大小受涂层热扩散系数与缺陷深度的大小影响。缺陷深度与热扩散长度的比值与涂层热扩散系数成反比，与缺陷深度成正比。

3）确定了缺陷深度等于1.5～2个热扩散长度的定量关系。利用盲频率得到热扩散长度，进而计算出缺陷深度是可行的。

[1] Baldan A. Adhesively-bonded joints in metallic alloys, polymers and composite materials: mechanical and environmental durability performance[J]., 2004, 39(15): 4729-4797.

[2] 沈功田, 王尊祥. 红外检测技术的研究与发展现状[J]. 无损检测, 2020, 42(4): 1-9, 14.

SHEN Gongtian, WANG Zunxiang Research and development status of infrared detection technology[J]., 2020, 42(4): 1-9, 14.

[3] 樊丹丹. 基于红外热波的界面脱粘无损检测技术研究[D]. 太原: 中北大学, 2011.

FAN Dandan. Research on Interface Debonding Nondestructive Testing Technology Based on Infrared Thermal Wave[D]. Taiyuan: Zhongbei University, 2011

[4] 李浩然, 朱玉玉, 武丽. 红外热成像无损检测系统锁相热激励源的研制[J]. 自动化仪表, 2017, 38(10): 91-99.

LI Haoran, ZHU Yuyu, WU Li Development of phase locked thermal excitation source for infrared thermal imaging nondestructive testing system[J]., 2017, 38(10): 91-99.

[5] Kim Won Tae, Choi Man-Yon. NDT analysis of metal materials with internal defects using active infrared thermography method[J]., 2006, 3(21): 835-840.

[6] BAI W, Wong B S. Evaluation of defects in composite plates under convective environments using lock-in thermography[J]., 2001, 12(2): 142.

[7] TANG Qingju, LIU Junyan, WANG Yang, et al. Subsurface interfacial defects of metal materials testing using ultrasound infrared lock-in thermography[J]., 2011, 16(3): 499-505

[8] 张金玉, 马永超. 基于红外锁相法的涂层脱粘缺陷检测与识别[J]. 红外技术, 2016, 38(10): 894-898.

ZHANG Jinyu, MA Yongchao. Detection and identification of coating debonding defects based on infrared phase-locked method[J]., 2016, 38(10): 894-898.

[9] 刘俊岩, 戴景民, 王扬. 红外图像序列处理的锁相热成像理论与试验[J]. 红外与激光工程, 2009, 38(2): 346-351.

LIU Junyan, DAI Jingmin, WANG Yang. Theory and experiment of phase locked thermal imaging for infrared image sequence processing[J]., 2009, 38(2): 346-351.

[10] 陈林, 杨立, 范春利, 等. 红外锁相无损检测及其数值模拟[J]. 红外技术, 2013, 35(2): 119-122.

CHEN Lin, YANG Li, FAN Chunli, et al. Infrared phase locked nondestructive testing and its numerical simulation[J]., 2013, 35(2): 119-122.

[11] 杨如意. 红外成像无损检测的缺陷定量化分析与应用研究[D]. 南京: 南京航空航天大学, 2009.

YANG Ruyi. Quantitative Analysis and Application of Defects in Infrared Imaging Nondestructive Testing[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.

[12] 田裕鹏. 红外辐射成像无损检测关键技术研究[D]. 南京: 南京航空航天大学, 2009.

TIAN Yupeng. Research on Key Technologies of Infrared Radiation Imaging Nondestructive Testing[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.

[13] 沈剑峰, 施柏煊. 激光诱导热波差分法分层检测金属次表面缺陷[J]. 光电子×激光, 2005(9): 1085-1088.

SHEN Jianfeng, SHI Baixuan. Layered detection of metal subsurface defects by laser induced thermal wave difference method[J]., 2005(9): 1085-1088.

[14] 钱鹏, 陆金桂. 基于PSO-BP神经网络的红外无损检测缺陷定量识别[J]. 南京工业大学学报: 自然科学版, 2019, 41(4): 501-507.

QIAN Peng, LU Jingui. Quantitative identification of defects in infrared nondestructive testing based on PSO-BP neural network[J].(NATURAL SCIENCE EDITION), 2019, 41(4): 501-507.

[15] 郭兴旺, 董淑琴. 基于小波变换的红外热波无损检测融合算法[J].光学技术, 2008(5): 659-663.

GUO Xingwang, DONG Shuqin. Fusion algorithm of infrared thermal wave nondestructive testing based on wavelet transform[J]., 2008(5): 659-663.

[16] 周辉, 钱美丽, 冯金秋, 等. 建筑材料热物理性能与数据手册[M]. 北京: 中国建筑工业出版社, 2010.

ZHOU Hui, QIAN Meili, FENG Jinqiu, et al.[M]. Beijing: China Building Industry Press, 2010.

Simulation of Defect Depth Detection Based on Infrared Phase Locking

NIU Yi1，WU Xi1，GAN Lingtong1，ZHOU Dechuang2

(1.,,430070,;2.,,230026,)

Defects in the paste structure inside a workpiece act as a crucial factor affecting production quality and operational safety, and infrared non-destructive testing can be used to detect and evaluate defects. In this study, the blind frequency of the paste structure at different defect depths and thermal diffusivity of the coating were measured through simulations, and the influence of the defect depth and thermal diffusivity of the coating on the blind frequency was studied. Relationship between the defect depth and thermal diffusivity of the coatings. The simulation results show that the thermal diffusion length can be obtained using the blind frequency, and a quantitative detection method for the defect depth can be obtained.

infrared nondestructive testing, paste defect, defect depth detection, lock-in thermograph

TP274.52

A

1001-8891(2023)10-1059-08

2022-05-06；

2022-05-25.

牛奕（1986-），男，博士，副教授，主要从事热安全科学机理，安全仿真与模拟的研究工作。E-mail：niuyi@whut.edu.cn。

周德闯（1980-），男，博士，高级工程师。主要从事低压火灾动力学，热安全仿真模拟等工作。E-mail：zhoudc@ustc.edu.cn。

国家重点研发计划（2017YFF0209704）；国家自然科学基金（51706164）；武汉理工大学自主创新研究基金（2018IVB056）。