磁悬浮轴承刚度、阻尼特性研究
李 雪 李峰岩 赵 聪 胡叨福
(珠海格力电器股份有限公司 珠海 519070)
引言
磁悬浮轴承通过电磁铁,电涡流位移传感器和功率放大器等环节,在反馈控制的作用下实现转子的稳定悬浮,具有无机械磨损、不需要润滑、噪声低的技术优势,在现代工业被广泛应用[1-3]。相比于传统机械轴承,磁悬浮轴承的刚度、阻尼具有在线校正控制的特点,可在线控制也是磁悬浮轴承的另一个技术优势。在磁悬浮轴承控制系统中,不确定的干扰力或冲击力会对整个系统的运行稳定性、动态响应、转子悬浮精度等产生非常大的影响,控制系统需要提供不同的刚度、阻尼去应对不同的外界扰动,而控制器不同,系统的等效刚度、等效阻尼将大不相同。因此,在磁悬浮系统中,探究控制系统中各控制环节对磁悬浮轴承刚度、阻尼的变化趋势的影响至关重要。
汪希平[4]以单自由度磁悬浮轴承角度分析了系统的刚度、阻尼系数与轴承结构参数、控制器响应之间的关系,并提出了复阻尼的概念。赵雷[5]基于独立PID 控制的磁悬浮转子系统,提出磁悬浮轴承的刚度、阻尼与所使用的校正控制器形式有关,并对各控制环节对刚度、阻尼的影响进行了分析。蒋科坚[6]提出一种不依赖于控制系统闭环传递函数的刚度、阻尼在线测量方法,通过闭环测试,反向推算开环特性,实现磁悬浮系统等效刚度、等效阻尼的辨识。吴华春[7]分别对控制器、传感器滞后、功率放大器衰减等因素进行了分析,基于频域等效法对磁悬浮轴承的支承特性进行了深入研究。而通过工程实验可知,电流环带宽是磁悬浮轴承控制系统中非常重要的因素,但目前对磁悬浮轴承等效刚度和阻比特性研究的文献多未考虑电流环带宽对其的影响,因此需要开展进一步的研究。
1 磁悬浮轴承数学模型
磁悬浮轴承本质上是一个非线性被控对象,电磁力是关于电磁间隙与轴承线圈电流的二次方函数,即非线性关系表示为:
式中:
k—力系数;
i—线圈电流;
x—电磁间隙。
磁悬浮轴承控制系统中,以主动式径向磁悬浮轴承为例进行分析,每个自由度均采用差动励磁方式,偏置电流与控制器输出的控制电流共同作用于轴承线圈,轴承线圈1 和轴承线圈2 产生的电磁力分别作用于转子,于是转子受到的总电磁力为:
式中:
I0—偏置电流;
ic—控制电流;
x0—额定间隙;
x—转子位移;
μ0—真空中的磁导率;
A0—电磁铁的磁极面积;
N—线圈匝数。
数学建模与仿真分析过程中,线性运算分析是控制系统的首选。当转子悬浮精度较好时,可将非线性模型等效成线性模型,这样可以更加方便的对转子受力进行分析。通常将方程(2)在平衡点处附近作泰勒展开并略去高阶无穷小量,得到平衡工作点下的磁轴承电磁力线性化方程,表达式如下:
式中:
ki—电流刚度系数;
kx—位移刚度系数。
方程(3)为受控对象的数学模型,在此基础上,加入磁悬浮轴承系统的控制器设计,便形成整个闭环控制系统。磁悬浮控制系统由外环位移控制和内环电流控制构成,其中,外环进行转子参考位移的跟踪,内环电流控制是系统动态响应性能的重要因素,其带宽直接决定了轴承线圈电流的跟踪与抗扰动能力。因此,有必要对磁悬浮轴承电流内环控制进行研究分析,将电流环带宽与磁悬浮轴承的等效刚度、等效阻尼建立关联,从更多的维度进行磁轴承的刚度阻尼特性分析。
电流环控制环路框图如图1 所示,参考电流为外环位置环的输出,轴承线圈等效为一阶惯性环节,电流调节器采用PI 控制器,参考电流与反馈电流之间的幅值和相位误差决定了电流环的跟踪性能。
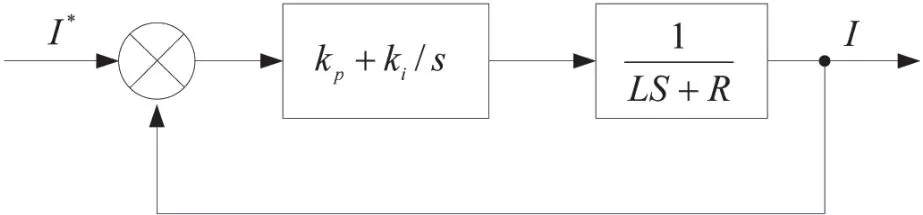
图1 电流环控制环路
由图1,电流环开环传递函数为:
式中:
kp—比例系数;
ki—积分系数;
L—线圈电感;
R—线圈电阻。
根据方程(4),可得电流环闭环传递函数为:
考虑到磁悬浮系统的动态响应,电流环的响应速度要足够快,因此,将电流环闭环二阶系统进行零极点对消,将电流环降阶成一个一阶惯性环节。将方程(5)进行变形整理,可得到:
式中:
令p1=1z,p1p2=Kz1,则此时电流环的闭环传递函数为:
式中:
ωb=p2—带宽。
此外,由p1=1z,可得:
由ωb=p2,联立方程(8),可得:
由方程(8)、(9)可知,电流环带宽与PI 参数和电感有直接的关系,电感不变的情况下提高电流环kp可有效拓展电流环带宽。
2 等效刚度和阻尼理论表达式
忽略高转速下的陀螺效应,磁悬浮轴承五自由度控制均采用分散控制,因此,以单自由度磁悬浮转子运动方程进行分析磁悬浮系统的等效刚度、等效阻尼,扰动力作用下,根据牛顿第二定律对转子运动方程进行拉式变换,可得:
式中:
m—转子质量;
Fd—扰动力。
控制过程中,电涡流位移传感器实时采集转子位置信息,在控制器和功率放大器等环节的作用下产生转子控制电流,因此,转子控制电流与位移关系可以表示为:
式中:
Gs(s)—传感器;
G(s)—控制器;
X(s)—振动位移;
Gp(s)—功率放大器。
不失一般性,将传感器Gs、控制器G 和功率放大器Gp均表示为复数形式,则控制电流与位移关系的频率特性函数可表示为:
M(ω)、N(ω)分别为等效传递函数Go的实部与虚部,将方程(12)代入方程(10),并将方程(10)表示为频率特性函数,可得:
相比于二阶力学系统中外力与弹簧刚度、阻尼的频率特性函数:
式中:
k—弹簧刚度;
c—弹簧阻尼;
F—外力。
通过类比,对应k 的是电磁轴承系统的等效刚度系数,记作Ke;对应c 的是电磁轴承系统的等效阻尼系数,记作Ce。即:
由方程(15)可知,磁悬浮轴承的等效刚度和等效阻尼并不是一个常量。在某一转速下,Gs、G 和Gp等环节的控制结构形式及参数直接影响磁悬浮系统的刚度与阻尼特性响应。
为了抑制转子位移误差突变产生的高频信号扰动及系统中的高频噪声,控制器环节采用不完全微分PID 控制器,表达式为:
式中:
Td—微分时间系数;
Tf—滤波时间系数。
功率放大器环节根据电流环等效传递函数可以表示为一阶惯性环节,表达式为:
在小量程位移变化范围内,传感器输出电压与位移变化成线性关系,因此,可将传感器环节等效为比例环节,用常系数进行表示,表达式为:
因此,将方程(16)、(17)、(18)分别表示为频率特性函数,并代入方程方程(15),得到磁悬浮系统的等效刚度、等效阻尼,表达式如下:
3 各参数对系统等效刚度和阻尼的影响分析
根据方程(19)、(20)中各参数变化对系统的等效刚度、等效阻尼的影响趋势进行分析,解析计算得到数据进行绘图处理,见图2。

图2 各参数对系统等效刚度、等效阻尼的影响
从图2 可以看出,不完全微分PID 控制器中kp、Td对轴承系统等效刚度、等效阻尼影响较大,可以明显看出变化趋势,变kp、Td参数控制便是基于此原理。而同一频率下,不同Ti几乎对等效刚度、等效阻尼无影响,所以实际调试过程中,找到一个合适的Ti后便不再发生改变。同时可以看出电流环bω对系统的等效刚度、等效阻尼影响也很明显,带宽为中高频时,系统的等效刚度、等效阻尼数值比较大,高刚度,大阻尼有利于磁悬浮系统的抗冲击控制,因此,控制系统中在不加强噪声影响的前提下尽量提高电流环带宽。
4 实验验证
在磁悬浮压缩机平台上验证了控制参数对磁悬浮轴承等效刚度、等效阻尼的影响。实验过程中,已将电流环带宽调整到最优值。图3 中,上面两条曲线依次转子前径向、后径向转子悬浮位移,升频过程转子悬浮精度比较差,为了保证系统的稳定运行,需要进行磁悬浮轴承的变刚度、阻尼控制,通过切换控制参数kp、Td,转子悬浮精度大幅提高,特别是后径向转子悬浮位移由793 mV 降低到333 mV,位移精度提高了约58 %。因此,在PID 控制框架下,通过调节控制参数的变等效刚度、等效阻尼控制可有效提高转子支承能力,改善转子悬浮精度,提高系统的运行稳定性。
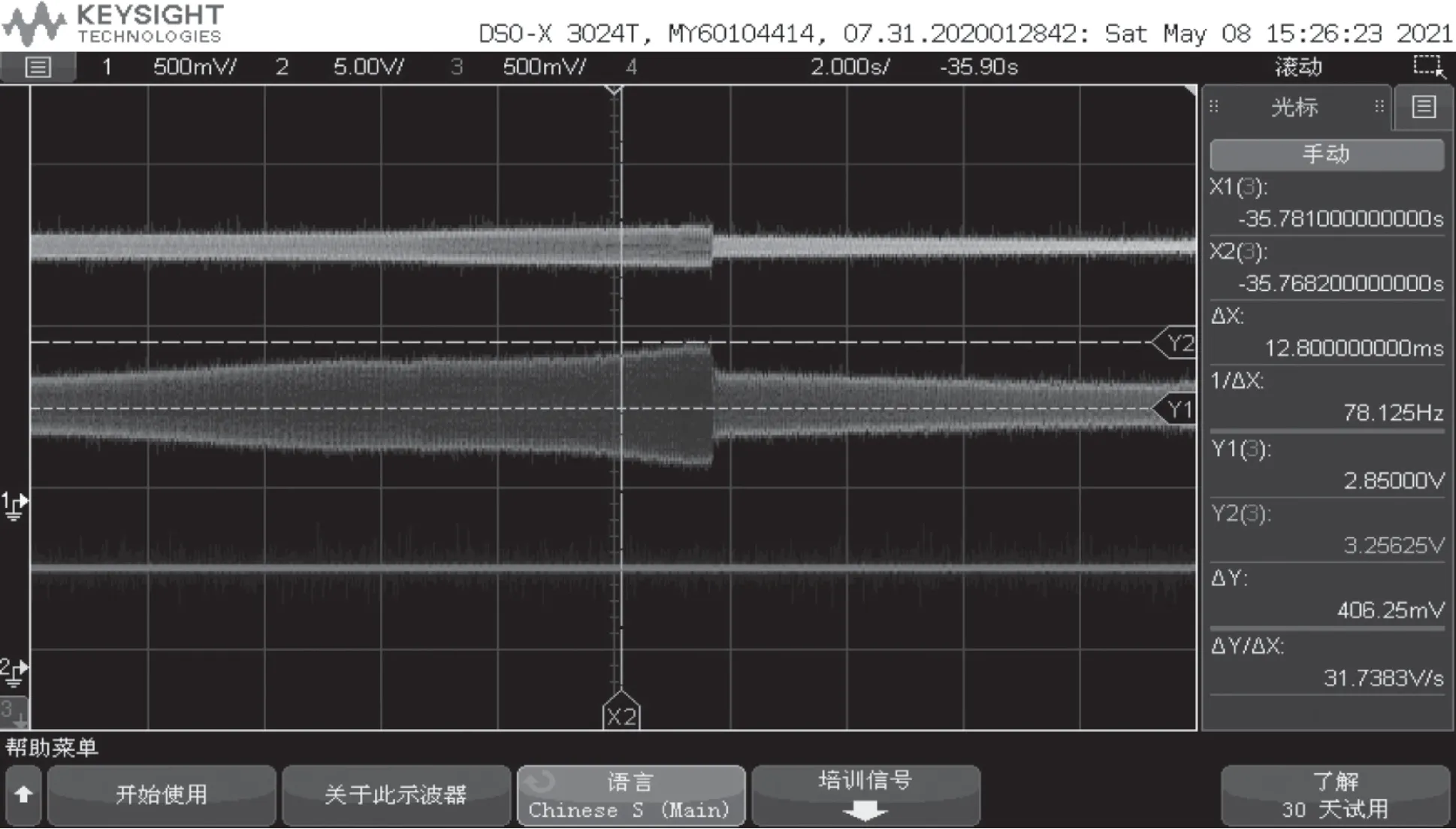
图3 磁悬浮轴承变刚度、阻尼实验
5 结论
本文分别对磁悬浮系统中的各控制环节进行数学建模,以不完全微分PID 控制为基础从理论上分析了控制参数、激振频率、电流环带宽对磁悬浮轴承等效刚度和等效阻尼的影响,同时结合实验证明了不同参数下的磁悬浮轴承支承能力不同,具有较强的工程实用意义。

