基于机器学习方法对台风浪短期预报应用

罗 锋,张 杰,全秀峰,汪 忆

(1.河海大学 港口海岸与近海工程学院,江苏 南京 210098;2.南通河海大学海洋与近海工程研究院,江苏 南通 226000;3.海岸灾害及防护教育部重点实验室,江苏 南京 210098)

引 言

台风是一种具有极强破坏性的气候现象,往往会对建筑物,沿海生态系统等造成较大危害。从台风发生的空间分布来看,西北太平洋是台风发生频率最高的区域,平均每年经过西北太平洋的台风数量约25.7个[1],占全球总数量的1/3[2]。我国濒临西北太平洋,是全球范围内受台风影响最大的国家之一,年平均有9.3个台风影响我国,位居世界之首[3]。台风在过境期间经常会形成风暴潮和大浪,造成海面水位上升,导致海堤溃坝,阻碍航行,危害港口码头及海上建筑的安全。因此,了解台风浪的规律,并进行准确预报尤为重要。当前有关台风浪预报的方法主要是借助数值理论模型,通过求解计算方程来模拟海浪,较为流行的主要有WaveWatchIII和SWAN,上述两种模型已被广泛应用于后报和预测的研究中[4-5]。虽然数值模型预报结果相对准确,但是具有计算时间慢,范围广,实时性不足的问题。

随着海洋监测站、浮标、观测船、遥感和再分析数据集的发展,每天能够收集到超过TB大小的海洋数据[6]。丰富的数据推动人工智能方法广泛应用于工程、水文和地球科学领域[7]。Yang等[8]使用支持向量回归的方法预测气候变化下水文变量规律。Deo等[9]使用人工神经网络技术成功预测印度东西海岸不同站点的潮汐。Asefa等[10]利用SVM方法实现对复杂海域的实际海流预测。王燕等[11]基于支持向量回归算法建立波浪短期预报模型,结果表明此方法更适用于小数据集并且可以有效解决预报中非线性问题,短期预报效果较好,长期预报准确性略低。王华等[12]基于BP神经网络建立波浪长期预报数值模型,预报准确率达到85%以上。Xi等[13]基于SWAN模型输出结果,通过使用多层感知机算法成功预测有效波高和波浪周期,并发现机器学习模型速度比物理模型快4 000倍以上[14]。Ma等[15]采用LSSVM方法对真实海浪进行模拟,并实现波浪数据的准确预报。金权等[16]利用支持向量回归算法对台湾岛东部海区进行海浪预报,结果表明对于随机性海浪要素预报精度比数值模拟更高。

机器学习方法已被广泛应用于波浪预报中,但目前结合机器学习的预报方法以常风浪最为普遍,对于台风浪的预报少有涉及。输入特征主要以风速分量和水深为主,结合空间性的研究少之又少。本研究将基于SWAN模拟结果和ERA-5再分析数据集,对比多层感知机、随机森林、支持向量回归三种典型机器学习算法的精度和效率,并探讨空间性特征对预报精度的影响,为机器学习在台风过境期间近海波浪预报的应用提供支撑。

1 数据与方法

1.1 数值模型

1.1.1 数据

地形资料来源分为两部分,深海区地形水深数据来源于Etopo1(www.ngdc.noaa.gov)全球地形数据集[17],近岸海域地形水深数据来源于海图水深资料。风场资料来源于ECMWF(www.ecmwf.int)的ERA-5再分析数据集[22],空间分辨率为0.25°,数据频次为1 h/次。李新文等[20]的研究表明,以再分析数据集作为SWAN的驱动风场进行模拟,模拟值与实测值误差较小,再分析数据集能够为SWAN提供驱动风场。台风资料由中国台风网[18-19](www.typhoon.org.cn)提供。考虑如下因素来选取模拟使用台风:1)台风路径经过中国东海;2)为了体现方法的普适性,所选台风要包含不同的路径,不同的等级;3)结合目前收集到的实测资料[20-21]。最后选取1509号“灿鸿”台风,1909号“利奇马”台风和2106号“烟花”台风。

1.1.2 SWAN模型

为保证后续机器学习算法的充足数据源,基于第三代海浪数值模型SWAN来模拟台风过境期间海浪的传播运动。SWAN由荷兰代尔夫特理工大学研发并维护[23],在模拟实际海域风浪时,模型以风场作为驱动,同时考虑了风能输入,白冠耗散,底部摩擦,水深导致的波浪破碎,非线性波相互作用,波浪绕射,波浪反射等多方面物理过程。适用于从数值水槽到大洋尺度的波浪或者风浪模拟。此外,SWAN模式针对模型结果输出提供了多种方法,其中包括点输出,面输出,曲线输出等,能够为后续构建机器学习模型提供充足数据。

由于水流影响下波作用密度守恒但波能密度不守恒,因此SWAN模式以动量谱平衡方程描述波浪运动,公式如下所示:

(1)

(2)

式中,N为动量谱密度;E为能量谱密度;cx和cy表示动量谱在几何空间的传播速度;cθ和cσ表示动量谱在频率空间和方向空间的传播速度;σ代表波浪相对频率;公式第4和第5项表示波浪受地形及水流影响在频率空间和方向空间的传播。Stot代表控制物理过程的源项,公式如(3)所示:

Stot=Sin+Snl3+Snl4+Sds,b+Sds,w+Sds,br

(3)

式中,Sin表示风输入项,Snl3表示三阶波-波相互作用,Snl4表示四阶波-波相互作用,Sds,w表示白冠耗散作用,Sds,b表示底摩擦作用,Sds,br代表由深度变化导致的波浪破碎。

1.1.3 模型设置与验证

中国东海波浪数值模型计算区域为25.4° ～ 36.8° N,118.7°～132.4°E,模型计算区域采用非结构化三角形网格进行剖分,模型网格尺度从远海60 km到近岸2 km,网格单元数为100 279,网格节点数为52 183,包括水上和陆上网格点,时间步长为3 600 s。本文收集到了台风过境期间近海浮标站实测波高数据[20-21],分别是舟山外海站(29.5° N,123.9° E),温州外海站(27.5° N,122.5° E),台州外海站(28.5° N,123.2° E)。

共设计三组试验方案如表1所示,为验证数值模型的准确性,选取验证站点对模拟结果进行验证,如图1所示,从图中可以看出,SWAN模型计算的各站点有效波高与实际情况吻合较好,并且能较好的模拟有效波高的极值和变化趋势,均方根误差在0.5～0.75之间。结果表明SWAN可以较好的模拟台风过境期间有效波高变化。

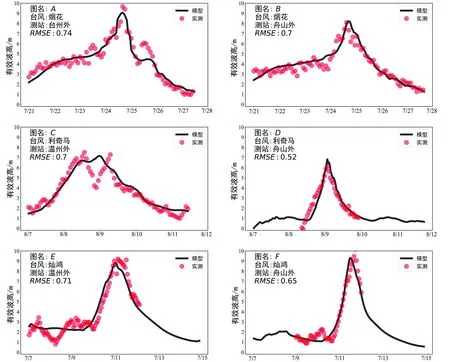
图1 烟花(上),利奇马(中),灿鸿(下)台风实测有效波高与SWAN模式结果对比[20-21]Fig.1 Comparison of Measured Significant Wave Heights and SWAN Model Results for Typhoons In-Fa(Top), Lekima(Middle), and Chan-hom(Bottom) [20-21]

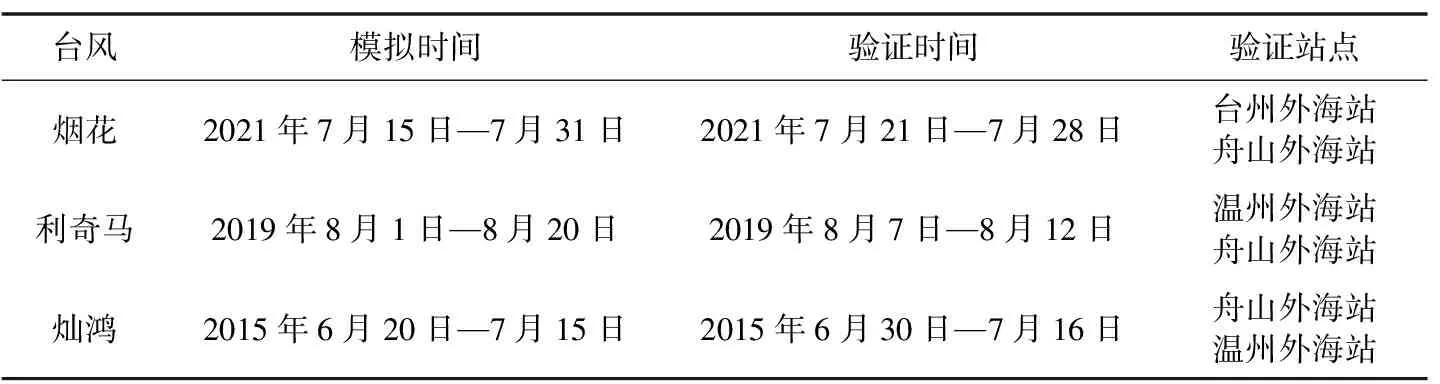
表1 模拟验证时间及验证站点

1.2 机器学习模型

1.2.1 数据集构建及预处理

原始数据集由SWAN模型的计算结果及ERA-5再分析数据组成,图2A为研究区域及台风路径,图2B为台风过境下输出区域及网格划分,在经度和纬度方向按照十六等分,网格节点为模型输出点,数据集的内容包括经度,纬度,水深,风速水平、垂直分量,平均波向,波峰周期,平均绝对波周期,有效波高。基于SWAN模型输出结果,构建训练集和测试集,按照时间进行划分,结果如表2所示。

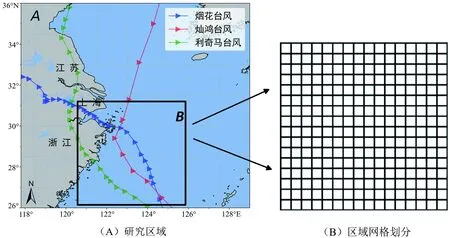
图2 台风路径及训练站点

表2 数据集划分

数据质量的好坏决定最后的预报效果,因此在训练前需要进行数据预处理。原始数据集中的参数数量级和单位相差较大,如果直接进行训练,则会导致训练模型偏向数值较大的特征,然而实际上这种特征与有效波高关联性较小,此外数量级差异过大会导致训练模型收敛速度变慢,预测准确度变低等问题。基于此将对原始数据集进行标准化,规范化操作,即Z-score标准化,计算公式如下:

(4)

式中,E(X)为数据平均值;D(X)为数据方差。在进行标准化后,处于同一数量级的输入数据能使预报模型训练效率更快,降低误差。

1.2.2 相关性分析

海洋数据特征具有复杂性和不确定性,此外海浪通常可分为风浪和涌浪,风浪是受局地风影响的海浪,随着海浪的传播远离产生地区,或者当传播的速度超过风速,则为涌浪。实际海洋环境中除了风浪还伴随着涌浪的作用。因此如果在预报模型中仅仅考虑风速,水深等特征,则无法取得较高的预报精度。

相关性分析是将所有特征与预测目标即有效波高之间进行分析,衡量两个要素之间的关联程度。统计学中常用的是皮尔逊相关系数和斯皮尔曼相关系数。皮尔逊相关系数主要用于呈正态分布的连续线性数据,而海洋环境数据虽然有规律,但不符合正态分布,不适用此方法;斯皮尔曼相关系数基于原始数据的排序位置进行求解,比较适用于分析海浪预报这种非线性数据。其计算公式如(5)所示:

(5)

式中,di表示两个数据次序的差值;n表示观测数据样本的量。斯皮尔曼系数范围是-1到1之间,大于0则正相关,小于0则负相关,绝对值越大,则表明观测值Y受到特征X影响越大。图3为有效波高与海洋各特征之间斯皮尔曼相关系数图,从图中可以看出,波峰周期相关系数小于0.05,可以认为其与有效波高之间关联程度很小,而风速分量、周期、水深和纬度与有效波高相关系数达到0.6以上,可以认为其与有效波高关联程度很大,这也符合上述提到的海浪实际物理背景。最终将波峰周期从数据集中剔除。

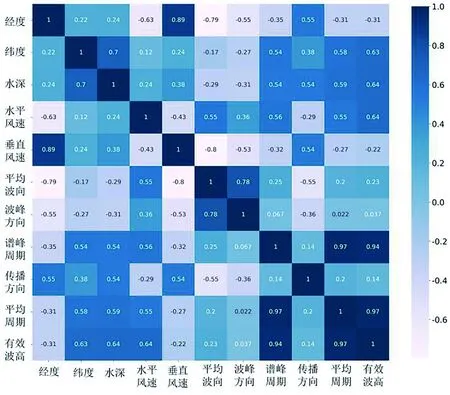
图3 波浪各特征之间斯皮尔曼相关系数

1.2.3 多层感知机预报模型

本文构建多层感知机模型,主要包括一个输入层,一个输出层和两个隐藏层,输入层通过输入风速、风向、水深和有效波高等参数,输入层的每个节点均对应着一组参数,并以一定的权重连接到隐藏层中的每个节点,隐藏层后会连接激活函数,其作用是将输入参数转换为输出的可微运算,保证没有负输出,本实验选取激活函数为“relu”,其公式为ReLU(x)=max(x,0)。MLP的训练方法是根据输出中的误差与损失函数(Loss function)中封装的预期结果相比调整连接权重和偏差,训练中通过正向和反向传播更新参数,并采用“Adam”优化器求解,“Adam”是由JAIS等[24]于2014年提出的随机目标函数优化算法。该方法易于实现,计算效率高,内存要求低,适合用于台风浪预报。

构建的多层感知机预报有效波高模型结构如图4所示,主要基于Python中的Sklearn开源包,每轮模型进行1 000次训练,并进行K=5折的交叉验证,避免模型出现过拟合和欠拟合,最终所采用的模型结构及超参数为:Adam优化器,(300,300)隐藏层,Relu激活函数,学习率采用“adaptive”,训练选取样本数为200。

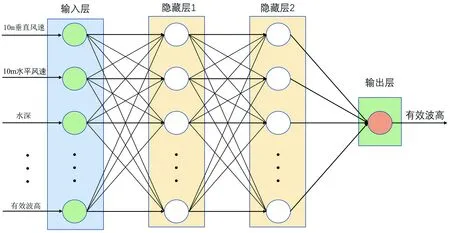
图4 多层感知机结构图

1.2.4 随机森林预报模型

随机森林算法是用于预测回归和分类目的最有效的机器学习算法之一。它是Breiman[25]提出的一种集成机器学习算法,使用多个并行决策树模型来训练和预测样本数据。不同决策树之间没有关联,回归的每个决策树都是一个非参数化的监督学习模型,它指出了一组分层结构的规则,以分支的形式做出决策,并从每个节点以叶子的形式获得真正的结果。随机森林的核心是装袋和特征采样两种随机化机制,确保树之间是独立并且彼此之间相关性较低。随机森林的最终预测是在回归的基础上对所有独立的决策树的结果求平均值。本文基于SWAN模拟结果构建随机森林预报波浪结构如图5所示。

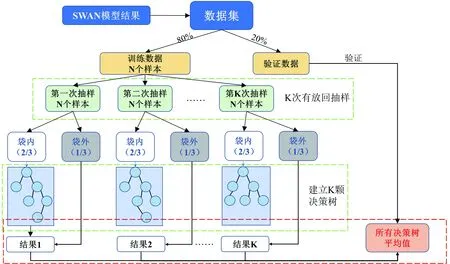
图5 随机森林海浪预报流程图

在构建每个决策树之前,从训练数据集中进行有放回随机抽样和替换迭代。过程中将每个样本组拆分为用于训练的数据,称为“袋内”,而训练树中未包含的数据称为“袋外”,用于评估,每颗树的目标是使袋外样本的平均误差(MSE)最小。由于每棵树都是独立且分布相同的,因此回归结果是K棵树的平均值。每轮模型训练1 000次,并行数量为4,避免模型出现过拟合和欠拟合,同时进行与多层感知机相同的交叉验证。

1.2.5 支持向量回归预报模型

支持向量回归(SVR)是支持向量机中最常见的应用形式,通过引入一个容忍偏差,最小化误差边界,以提高模型的泛化性。SVR的优点之一是可以避免在高维特征空间中使用线性函数的困难,并将优化问题转化为双凸二次规划。SVR生成的模型仅依赖于训练数据的子集,因为用于构建模型的成本函数会忽略任何接近模型预测的训练数据(在阈值内)。SVM 回归函数为f(x)=[wφ(x)]+b。模型参数如表3所示。

表3 RMSE误差分析结果表

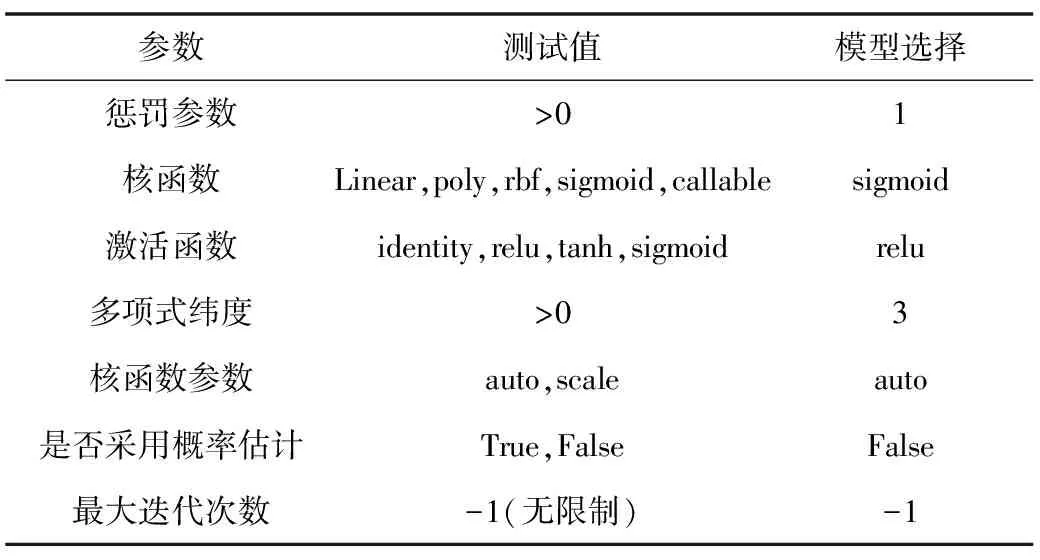
表3 支持向量回归结构及参数

2 评估指标及结果分析

2.1 评估指标

为定量分析预报结果的误差,引入决定系数(R2)和均方根误差(RMSE)进行预报结果精度分析,计算公式分别如(6)和(7)所示:

(6)

式中,R2为拟合优度,表示有效波高能够被“特征”解释的比例,取值范围为0≤R2≤1,R2越接近1,说明机器学习预报模型所建立的“特征”与有效波高关系越强。

(7)

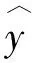
2.2 结果分析

通过SWAN模拟“灿鸿”,“利奇马”和“烟花”台风过境期间中国东海波浪场,并基于模拟输出结果分别构建多层感知机,随机森林,支持向量回归预报模型。同时对比加入空间性特征前后有效波高的预报精度,预报结果如图6所示,图中每一排表示基于三种机器学习算法对同一台风过境下的波浪预报结果;每一列则表示同一机器学习算法对不同台风过境下的波浪预报结果。红色和绿色折线分别代表未加入空间性特征和加入空间性特征的波浪预报结果。蓝色点表示SWAN模拟输出结果。

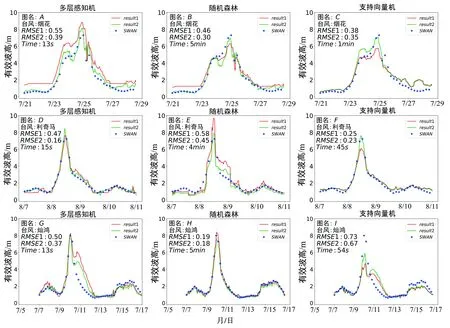
图6 站点有效波高预报精度

从图中可以看出,当加入空间性特征后,预报模型均方根误差降低,模型精度得到提高,其中多层感知机拟合优度平均提高18%,均方根误差平均降低40.4%;随机森林拟合优度平均提高6%,均方根误差降低20.8%;支持向量回归拟合优度平均提高7%,均方根误差降低8.7%。表明空间性特征在构建机器学习预报波浪模型中起着重要作用。通过纵向对比,同一种方法在预报不同台风过境期间的有效波高误差相差较小,能有效的预报波高变化趋势,并且对于极端值的灵敏度基本一致(即是否能够有效预报出极值),这表明机器学习算法能够在台风过境期间对有效波高进行预报。通过横向对比,可以发现,随机森林在预报中的误差普遍低于另外两种方法。此外,从图中可以看出,多层感知机预报速度最快,其次是支持向量机,最后是随机森林,这可能是因为构建的多层感知机模型只包含一个隐藏层,所以训练速度较快,当隐藏层的数量增加时,模型可以学习更加复杂的情况,但训练速度会降低,容易发生过拟合。随机森林训练时间主要受到决策树的数量影响,当决策树的个数较多时,训练所需的时间就越长。支持向量回归训练时间主要受到迭代次数的影响,迭代次数越多,训练时间越长。

3 结论

基于第三代海浪模型SWAN的模拟结果,通过多层感知机,随机森林,支持向量回归三种机器学习方法,构建“灿鸿”,“利奇马”和“烟花”极端天气下波浪预报模型,并对三种机器学习方法在引入空间性特征前后的预报精度和预报模型所需时间进行了系统分析,误差分析如表3所示,并结合图6可得到:

(1)在时间耗费上,多层感知机由于其结构简单训练速度较快,不超过15 s;而支持向量回归和随机森林由于其结构复杂性训练时间达到几分钟。

(2)在预报精度上,当三个模型中加入空间性特征后,模型预报精度明显提升,其中多层感知机均方根误差平均降低40.4%,随机森林均方根误差平均降低20.8%,支持向量回归均方根误差降低8.7%,表明在构建机器学习预报波浪模型中,需要考虑空间性这一特征。

(3)从所有预报结果来看,随机森林预报精度较高,并且能有效的预报波高极大值和变化趋势。主要原因是随机森林是一种集成学习,内部由多个决策树构成,当决策树的数量和深度增加并趋向于无穷时,模型的误差会趋向收敛值。

在未来进行波高预报时,多层感知机和支持向量回归训练速度快于随机森林,但精度不如后者,三种方法都能提供相对较为可靠的预报结果,在以后基于机器学习的台风浪预报中,要根据具体情况进行模型的选择。本文工作中,模型输入除了传统的风速特征等,还首次引入了空间性特征,通过对比三种方法的预报精度,结果表明空间特征对有效波高的预测有着重要作用,在以后的研究中不能忽视。