基于应力波卷积神经网络的齿轮故障诊断方法

花海波，于洪亮，闫 锦，廖建彬

(集美大学轮机工程学院，福建 厦门 361021)

0 引言

齿轮箱作为机械设备中的一种必不可少的连接和传递动力的通用零部件，在农业机械、运输机械、冶金机械等现代化工业设备中得到了广泛的应用[1]。在船舶制造领域，船用齿轮箱是船舶的核心部件，目前研究的重点主要集中在船用齿轮箱的非线性振动特性、动力学分析等[2]，关于船用齿轮箱故障机理方面的研究较少。齿轮的不同类型及不同程度的齿轮故障远超轴承故障[3]，研究齿轮故障诊断技术，分析齿轮故障机理，可以更加及时准确地判断齿轮的运转状态，并以此为依据对设备进行保养和维修，这对保障机械设备平稳运行，避免因齿轮故障而造成重大事故等具有重要的意义。

传统的齿轮故障诊断方法包括倒谱法和Hilbert解调法[4]，这两种方法分别针对齿轮运行过程中由故障冲击引起的频谱边带及共振调制现象。从本质上来说，由于齿轮的故障而导致运行过程中产生额外力载荷，加速度传感器在采集振动信号时会影响旋转机械的正常振动信号，这种影响在使用传统诊断方式时，对正常信号的畸变只占其比例的5%～10%[5]。当齿轮处于初始故障时，其影响甚至更低，因此，对于齿轮的故障诊断方式也一直在不断改进。近年来，深度学习成为机械智能故障诊断的一种主流趋势[6]。为了克服BP神经网络学习效率低、收敛速度慢的缺陷，陈立爱等[7]将SOM神经网络与BP结合，构成复合神经网络，其实时性与自主学习性均得到较大提升。薛萍等[8]针对BRF神经网络在非平稳工况下齿轮故障诊断检测困难的问题，引入了CEEMDAN算法，提高了故障诊断的有效性和准确性。上述几种方式均是针对某一类信号的故障诊断算法，在诊断算法效率一致的状况下，其诊断准确性非常依赖于原始信号。目前有两种方式可以弥补单一信号在故障诊断上容错能力不佳，故障信息有限的缺点[9]。1)提高信号的信噪比，使信号的有效分量提升，凸显故障特征，包括诊断分析[10]、声发射分析[11]、热成像技术[12]等。胡茑庆等[13]通过经验模态分解对采集到的信号进行提取，结合深度卷积神经网络进行特征融合，实现对齿轮箱的故障诊断。Zhang等[14]提出改进的复合多尺度模糊熵，并将其应用于故障特征提取。2)使用信息融合的方式可以较为全面、准确地反映设备运行状态，从而提高故障诊断精度[15]。王伟源[16]为了对齿轮箱故障做出准确的判断，测试数据不仅包含振动信号，还包括油液中磨粒含量数据，这使得诊断算法具备更多维的判断依据。以上算法均是在基于信号本身，而不考虑故障的应力传播特征情况下进行的，或者是采用特殊传感器或多传感器进行协同诊断，在实际故障诊断环境中实施难度大。本文采用最常见的加速度信号传感器，使用应力波信号提取算法对故障特征进行提取，并结合小波变换及卷积神经网络以达到对齿轮故障进行诊断的目的。

1 基本理论

1.1 故障齿轮运转过程中应力波现象

因此在激励点之外应力波会随着距离增加而产生衰减，而持续时间会增加。当故障发生时，机器表面产生应力波，由此对运动传感器波产生一个输入信号，传感器收到应力波信号后随之产生一个对应的响应。应力波现象是一种短时瞬态事件，其分布频带宽，频率范围1～15 kHz，甚至可以扩展到50 kHz。一般来说，在采集的信号中，正常的振动信号其倍频分量分布位于比应力波分量更低的频带中。为了将应力波信号分离，需要将信号通过高通高阶滤波器进行滤波。经过滤波后，应力波信号比重增大，为了确定故障的特征与类型，需要量化该应力波信号的一些特征，主要包括应力波的幅值，故障激励特征信号的持续时间以及应力波冲击信号的周期性(与部件转速及机器转速有相关性)。

抽取高频应力波分量后还需要对信号进行峰值抽取，而峰值则是滤波信号中一段固定时间间隔中的值。一般情况下，时间间隔的选取是根据分析频率带宽而定的，选取原则需保证在最高的故障频率周围也能够得到足够的采样点数。

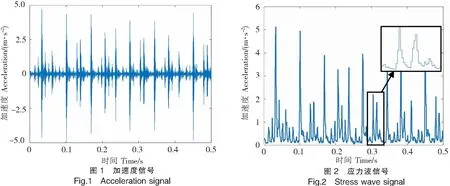
峰值数据块的长度取决于轴转速和原始数据时间间隔。图1中的原始加速度信号在经过高通滤波(截止频率为1～2 kHz)包络检波后可初步将低频干扰信号从振动信号中剔除，之后再对信号进行等间隔重采样，以匹配应力波冲击特征(一般重采样频率为2.56fmax，fmax为分析频率)，为了保持应力波信号的强度，在重采样区间内对每个区块进行峰值提取，以提升应力波信号的频谱峰值占比。经过上述处理后即可得图2所示的应力波信号。可以看出，经过以上的预处理，应力波的幅值和频率得到了较好的保持。

1.2 卷积神经网络

卷积神经网络(CNN)作为一种前馈神经网络，具有强大的特征提取能力，可以将输入层原始数据逐层转化为更易于识别的特征[18]。CNN通过设定卷积核，对图像特征进行提取，有效地从大量样本中学习特征表达，模型泛化能力更强。

在使用CNN算法对应力波信号进行处理前，为了使数据更加符合卷积神经网络的处理需要，使用连续小波变换(continuous wavelet transform，CWT)对应力波信息进行前处理。经过小波变换可以将一维时域信号转换为在时域和频域两个维度上能量强度的时频图谱。另外为了充分利用二维卷积神经网络在图像特征提取方面的优势，采用morlet小波作为小波基函数对应力波信号进行连续小波变换，改变morlet小波基函数的尺度与平移，应力波在时域上与信号的相关性以积分运算的形式体现，通过积分运算可以获得数据片段的频率特征。

应力波信号经过CWT处理后，一维应力波信号转换为二维时频信号，在反映应力波信号频率的同时，还可以反映变化趋势，为卷积神经网络识别信号特征提供更多判断依据。

经过上述步骤处理所得的二维时频应力波信号即构成了CNN算法的输入层，除输入层外，CNN主要组成部分还包括卷积层、池化层和全连接层，CNN算法的整体结构如图3所示。

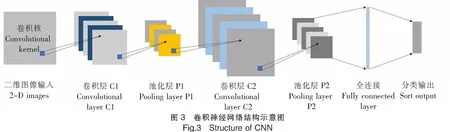
一个卷积层一般包含一个或多个不同的卷积核，卷积核以指定步长进行滑动卷积，提取输入数据的图形特征。卷积层的数学模型为

(1)

池化层用于压缩数据和参数的量，增强数据特征的不变性。池化层的数学模型为

(2)

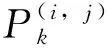
卷积神经网络的目标损失函数为

(3)

式中：xi为样本数据；yi为样本数据的标签值；n为样本集容量，f(xi)为经过卷积神经网络处理的预测结果。

1.3 应力波特征提取及故障诊断算法流程

相比于原振动加速度信号，应力波信号与故障特征的相关性更强，在使用卷积神经网络对故障进行诊断前，采用应力波特征提取算法对振动加速度信号进行预处理，可以提升神经网络算法的收敛速率及诊断准确率。基于应力波特征提取的卷积神经网络故障诊断算法的具体步骤如图4所示。

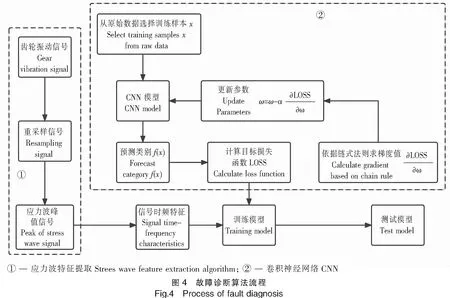
为了使卷积神经网络模型更加完善，预处理信号先按比例划分训练集、验证集、测试集。在对划分好的数据集进行的应力波特征信号提取之后，为了获取卷积神经网络所需的输入集，将应力波特征信号进行小波变换，其变换结果作为输入量参与模型的建立，并以验证集对该模型进行完善，最终以测试集作为检测数据获得模型精度及诊断误差等结果。以美国凯斯西储大学轴承数据集为基础，使用采样率为12 kHz下的原始驱动端轴承振动数据，在模型学习率设置为0.5‰以及迭代20轮的条件下，验证无负载时内圈故障、外圈故障、滚珠故障、正常轴承分别在1797，1772，1750 r/min工况下的诊断结果，其输出特征降维图如图5所示。

图5表明四种轴承在三种工况下的故障特征聚集性均较好，对诊断结果进行统计可发现，若使用原始信号二维时频谱作为输入集，在1797，1772，1750 r/min转速下对故障轴承进行诊断的故障误判率分别为1.4%、1.1%、1.3%，而在对信号进行应力波特征提取后，其诊断误判率分别降低至0.9%、0.5%、0.8%，初步验证了该算法的有效性。

2 试验方法与算法验证

针对基于应力波卷积神经网络的齿轮故障诊断算法，设计齿轮故障检测及诊断实验，实验采用旋转机械故障模拟试验台，如图6所示。

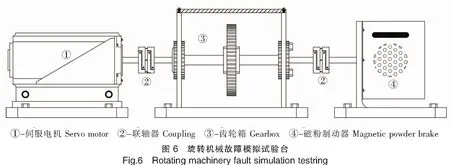
伺服电机与齿轮箱以及齿轮箱与负载轴均采用联轴器连接，齿轮箱包括两个齿轮，小齿轮为主动轮，齿数为27，大齿轮为副齿轮，齿数为73。

实验中设置采样频率为51.2 kHz，采样时间为21 s，转速为1500 r/min。两种模拟故障分别设置为大齿轮断齿和大齿轮点蚀。

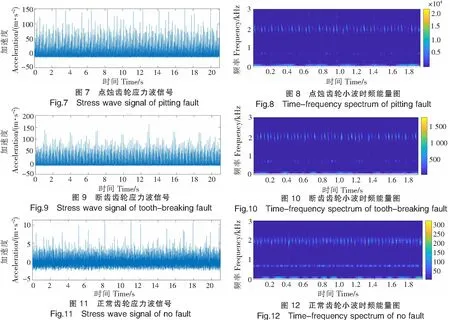
实验采集得点蚀、断齿和正常齿轮的振动加速度信号，使用Morlet小波为小波基函数对所采集的齿轮振动信号进行分析。将原始振动信号进行应力波信号提取后的波形以及对应的小波变换时频图如图7～图12所示。

合适的卷积神经网络对模型收敛速度及诊断正确率有明显的影响。第一层卷积主要对二维时频图像进行局部特征的提取，池化层对所提取的特征进行降重采样，去除冗余特征提取，减少模型多余的特征参数；第二层和第三层卷积层以及池化层进行重复的卷积运算，进一步提取与故障类型相关程度较高的特征参量，降低输入特征的模糊性；然后在全连接层的作用下将二维特征展开成一维向量，并将一维向量映射至样本空间；最后经过式(3)交叉熵损失函数实现齿轮故障类型的划分。

卷积神经网络的结构参数如表1所示。

表1 卷积神经网络结构参数表Tab.1 The Parameter of CNN

模型采取前3/4的数据作为训练集，后1/4的数据作为模型准确度验证集，将三种状态的小波时频能量图以二维向量的形式作为CNN网络的输入集进行模型训练，其最终可得模型误差矩阵，如图13所示。

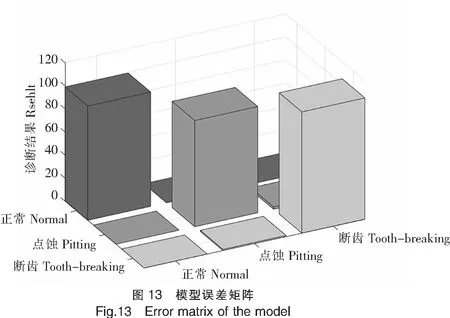
从图13所示的模型误差矩阵可以发现，经过训练产生的故障诊断模型进行检验后，正常齿轮信号与点蚀、断齿的故障特征没有误诊断，但点蚀故障和断齿故障之间会产生一定的混淆。其中点蚀故障有2.17%的概率可能会被误诊断为断齿故障，断齿故障有0.95%的概率被误诊断为点蚀故障。从图8，图10和图12来看，无论是点蚀还是断齿，其应力波能量相较于正常齿轮要更为集中，但在时域上并不十分稳定，这可能是导致点蚀和断齿故障存在相互误判的原因之一。另外，受限于模型初始化参数以及模型误差与迭代后的模型精度等因素，也可能导致一定的诊断误差。从总体来说模型在不同故障样本上的分类具有较好的效果，说明该方法是有效性的。

在应力波信号与原始信号两种输入集下，模型迭代的准确率变化曲线如图14所示，模型损失值变化趋势如图15所示。

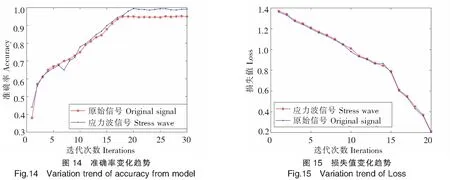
由图14可见，在多次迭代中，随着横轴迭代次数增加，纵轴原始数据集及应力波信号数据集准确率前期上升速度明显，平稳收敛至最大值，但两者仍有差异。依据原始振动加速度信号的诊断模型最终收敛接近于95%，而依据应力波信号的模型最终准确率近99.5%，模型准确度提升4.74%，效果明显。然而损失值变化趋势差异不明显，以相似速率收敛，未产生过大偏差，说明模型在训练中未发生过拟合现象，所使用的训练集训练所得模型在模型测试集上泛化性较优。

3 结论

本文提出了一种齿轮故障特征提取及故障诊断算法，给出了基于振动加速度信号的应力波特征提取方法及应用卷积神经网络对齿轮箱故障进行诊断的方法。基于西储大学轴承数据集进行算法验证，无负载，在转速分别为1 797，1 772，1 750 r/min时对四种轴承状态(内圈故障、外圈故障、滚珠故障、无故障)的诊断正确率分别达到35.7%，54.5%，38.5%，证明了该算法在轴承故障诊断中的有效性。

从故障诊断算法对实验原始数据及应力波特征信号的诊断结果来看，在迭代步数相近的情况下，模型诊断精度由95%提升至99.5%，诊断性能提升明显，说明该算法对于齿轮故障诊断也同样有效。后续可将该算法应用于其他传动结构或旋转部件的故障诊断。