Douglas-Peukcer抽稀算法在水文中的应用及编程实现与优化
代 斌,施 艺
(四川省成都水文水资源勘测中心,成都 611130)
0 引言
水文学是研究水资源、水循环和水环境的科学,涉及大量的水文数据。随着信息技术的快速发展和数据采集技术的成熟,水文学领域也迎来了大数据时代。在目前的大数据环境下,水文数据的数据量呈现爆炸式增长,传统的数据处理方式已经无法满足需求,数据抽稀成为了处理数据的一种关键技术,也是现在水文数据管理和分析的必要手段。
水文数据抽稀是指在保持水文数据重要特征的同时,从原始水文数据中有选择地减少数据点的数量,以达到减少数据量、提高计算效率、降低存储成本和提高数据质量的目的。
1 抽稀算法的选择
1.1 常用算法
目前来说抽稀较为常用的算法有:等步长法、线段过滤法、垂距限值法及Douglas-Peuker算法。
水文数据是按时间顺序排列的数据点集合。等步长法是按照一定的间隔距离对点集进行抽取,其余点全部压缩掉,在相邻抽取点间用直线连续;线段过滤法是从点集的第一点开始,若连续两个点组成的线段长度比给定的阈值小时,删除这两点,并将这两点的中点插入两点原来的位置;垂距限值法是从点集的第一点开始,根据中间点到前、后两个相邻点连线的距离,来确定是否保留该点的一种抽稀算法,当距离大于给定的阈值时保留该点,否则删除该点;Douglas-Peukcer算法是计算点集中除头尾两个端点外的每个点与头尾两点直线之间的垂直距离,若这些距离的最大值小于给定的阈值就删除这一组点,若大于给定的阈值,则从最大距离处将点集分为两部分,继续以上步骤,该算法以递归方式应用于这两个部分,直到达到所需的简化级别[1]。
1.2 算法选择
将水文数据的点集看作是以时间为x轴、数据值为y轴的一条连续曲线,在以上四种抽稀方法中,等步长法在这四种方法中显然是相对较差的一种方法,因为它完全不关心原始曲线的数据是什么,只是按照给定的步长去抽取数据。若步长较小,抽稀效果不明显;若步长较大,则原始曲线严重失真[1]。
另外三种方法与等步长法有明显的不同,因为它们的抽稀都会关系原始曲线中数据之间的联系。而从它们观察的对象来看,线段过滤法观察的是两个点之间的距离,垂距限值法观察的是三个点之间的关系,而Douglas-Peukcer算法观察的是整条曲线中各个点的关系。从设计思路上来看,Douglas-Peukcer算法的抽稀效果是相对较好的,线段过滤法的抽稀效果是相对较差的[1]。
垂距法较等步长法与线段过滤法精度更高,同样具有算法简单和易于实现等优点,但它是一个局部的算法,无法从整体上考虑线要素的变化形态。因此,当各相邻点起伏变化不大时,即使给定的阈值较小,也可能会删除掉构成大弯曲形态上的所有中间点,造成线要素形态失真[2]。
Douglas-Peukcer算法的优点是它是一个整体算法,能做到在删除与保留之间达到较好的平衡,即能充分减少点的数量,又能尽量保留特征点[2]。但Douglas-Peukcer算法较其余算法更复杂,实现时需要采用递归方法,有一定的难度。本文选取Douglas-Peukcer算法进行水文数据的抽稀,并对其在编程中的实现进行了分析探讨。
2 在编程中的实现与优化
2.1 算法实现
目前遥测技术已经得到广泛应用和普及,动辄5 min甚至1 min一个的数据虽然可以帮助我们更及时地掌握水文信息以及更精细化地进行水资源管理,但在数据存储的成本、数据的分析整编、计算所需的时间和资源、数据可视化效果上都带来了不少的麻烦,需要先对数据进行抽稀处理后再进行应用。因此,本文以遥测水位数据为例,对Douglas-Peukcer抽稀算法的实现进行分析探讨。
为方便普通职工在EXCEL中调用该过程,本文采用VBA语言进行编译,实现代码如下:
Function Compr_DP(Arr_COMPR, Arr_TEMP, Start_Index, End_Index)
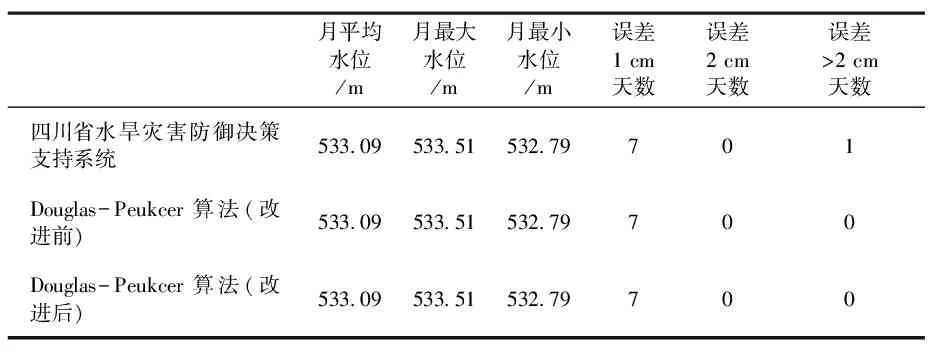
If Start_Index Dim Start_X#, Start_Y@, End_X#, End_Y@ Start_X = Arr_COMPR(Start_Index, 1): Start_Y = Arr_COMPR(Start_Index, 2) End_X = Arr_COMPR(End_Index, 1): End_Y = Arr_COMPR(End_Index, 2) Dim i&, Index&, Dist@, Max_Dist@, Point_X#, Point_Y@ For i = Start_Index + 1 To End_Index - 1 Point_X = Arr_COMPR(i, 1): Point_Y = Arr_COMPR(i, 2) Dist = Calc_DIST (Start_X, Start_Y, End_X, End_Y, Point_X, Point_Y) If Dist >Max_Dist Then Index = i: Max_Dist = Dist Next i If Max_Dist >3 Then Arr_TEMP(Index, 1) = Arr_COMPR(Index, 1) Arr_TEMP(Index, 2) = Arr_COMPR(Index, 2) Call Compr_DP(Arr_COMPR, Arr_TEMP, Start_Index, Index) Call Compr_DP(Arr_COMPR, Arr_TEMP, Index, End_Index) End If End If End Function Function Calc_DIST#(Start_X, Start_Y, End_X, End_Y, Point_X, Point_Y) Dim a, b, c, p, S a = Abs(Sqr((Abs(Start_X - End_X) ^ 2) + (Abs(Start_Y - End_Y) ^ 2))) b = Abs(Sqr((Abs(Start_X - Point_X) ^ 2) + (Abs(Start_Y - Point_Y) ^ 2))) c = Abs(Sqr((Abs(Point_X - End_X) ^ 2) + (Abs(Point_Y - End_Y) ^ 2))) p = (a + b + c) / 2 S = Sqr(Abs(p * (p - a) * (p - b) * (p - c))) Calc_DIST = S * 2 / a End Function 其中Function Compr_DP是主过程,阈值设定为3(cm),根据曲线上所有点的坐标依次计算各点到Start、End两点所在直线的垂直距离(通过调用Function Calc_DIST),得到最大距离Max_Dist,若Max_Dist小于阈值3,则将这条曲线上的中间点全部舍去,以直线段作为曲线的近似,该段曲线处理完毕,若Max_Dist小于阈值3,保留Max_Dist对应的坐标点,并以该点为界,把曲线分为两部分,对这两部分重复使用该方法,直到所有Max_Dist均小于阈值3,即完成对曲线的抽稀;Function Calc_DIST是子过程,通过3个点的坐标求得各点到Start、End两点所在直线的垂直距离。 图1 Douglas-Peukcer算法示意 上一章节中,我们计算得到的距离是各目标点到Start、End两点所在直线的垂直距离,即目标点与Start、End两点形成的三角形的高,而与大部分其他类型的数据集是以空间为坐标进行分布不同,水文数据基本上都是以时间为序列进行分布,我们可以将各目标点到Start、End两点所在直线在同一坐标轴(即以同一时间为参考)的距离代替垂直距离,这样既能减轻计算量(将三角运算变为加减乘除),又更符合水文数据以时间为序列进行分布的特征。由于在VBA中默认的时间运算以d为单位,而水文计算中水位默认以m为单位,我们以更精细的刻度来保证计算的准确性,以 min为时间单位、以cm为水位单位。通过修改子过程Function Calc_DIST的代码完成以上内容,实现代码如下: Function Calc_DIST@(Start_X, Start_Y, End_X, End_Y, Point_X, Point_Y) Dim a1&, a2&, b1&, b2& a1 = (End_X - Start_X) * 1440 If a1 = 0 Then Calc_DIST = 0: Exit Function a2 = (Point_X - Start_X) * 1440 b1 = (End_Y - Start_Y) * 100 b2 = (Point_Y - Start_Y) * 100 Calc_DIST = Abs(b2 - b1 * a2 / a1) End Function 图2 Douglas-Peukcer算法(改进后)示意 为验证以上代码的实际运行效果,本次分析以石堤堰水文站实测水位资料为实例样本,对Douglas-Peukcer算法改进前后的效果,以及跟四川省水旱灾害防御决策支持系统的抽稀处理进行对比(阈值均设置为3 cm)。 抽稀算法的优劣,一般通过数据处理时间、数据抽稀率、数据偏差来评价。数据处理的速度(时间复杂度)主要以运行时间来评价;数据抽稀率(空间复杂度)是抽稀掉的数据点数与原始数据点数之比。数据偏差依据《水文资料整编规范》(SL/T 247-2020)要求,处理后的水位变化过程完整,经处理以后计算的日平均水位与采用所有数据计算的日平均水位相差不宜超过2 cm[3]。我们分别对抽稀前后的水位数据进行整编,通过对比抽稀前后得到的日平均水位及月最大、最小、平均水位进行数据偏差评价。 对石堤堰水文站2022年全年共98 488个水位数据进行抽稀处理(见表1),四川省水旱灾害防御决策支持系统的抽稀用时14.9 s,抽稀数据81927条,抽稀率83.2 %;Douglas-Peukcer算法(改进前)用时12.7 s,抽稀数据87108条,抽稀率88.4 %;Douglas-Peukcer算法(改进后)用时3.47 s,抽稀数据86707条,抽稀率88.0 %。通过对比,四川省水旱灾害防御决策支持系统抽稀用时最长,抽稀率最低,改进前的Douglas-Peukcer算法抽稀率最高,但数据处理的用时较长,改进后的Douglas-Peukcer算法数据处理的速度明显更快,且抽稀率与改进前相差不大,在时间复杂度与空间复杂度上均能达到比较满意的效果,效率最佳。 表1 抽稀算法实际运行效率比较 由于全年遥测数据量较为庞大,对未抽稀的原始数据进行整编难度较大,因此本文采用单月数据进行数据偏差比较,以石堤堰水文站2023年5月水位资料为样本,各算法与未抽稀前的整编成果对比见表2。 表2 抽稀算法实测数据偏差比较 通过与原始数据的整编成果进行对比,各算法的成果均能满足《水文资料整编规范》(SL/T 247-2020)要求,Douglas-Peukcer算法较四川省水旱灾害防御决策支持系统稍好,算法改进后效果与改进前基本一致。 将抽稀前后的水位过程线进行对比,选取5月1日8时至5月2日8时的时间段,可以看出,在大部分时间,Douglas-Peukcer算法的水位变化过程都更贴合原始数据,算法改进后效果与改进前基本一致。 图3 水位过程线对比 本文对Douglas-Peukcer抽稀算法及其与其他抽稀算法的优劣进行了简要的分析,通过编程实现了Douglas-Peukcer抽稀算法在水文中的应用,并根据水文数据的特性对算法进行了优化。本文根据石堤堰水文站实测资料为实例样本对算法进行了运行效率测试与数据偏差分析,Douglas-Peukcer抽稀算法在各方面均领先于四川省水旱灾害防御决策支持系统的抽稀处理算法,改进后的Douglas-Peukcer抽稀算法在处理效果上与改进前基本一致,但在运行效率上较改进前有较大提升,实现了高效率、高抽稀率与保真效果之间的平衡。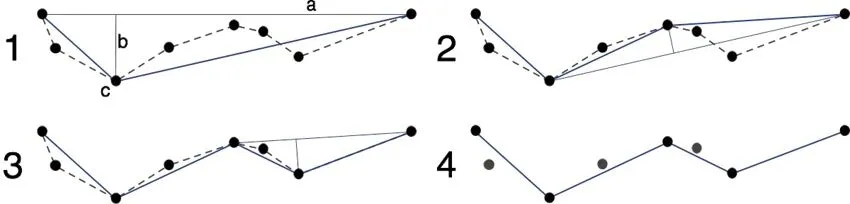
2.2 算法优化

2.3 实例计算与分析


3 结语

