基于海底电缆抢修的可重构式履带机设计与分析

张维佳, 蔡 驰, 郭 强, 王思宇, 王亚东, 陈泳伽, 王士喜, 谭绩臻

(1.中国南方电网有限责任公司 超高压输电公司广州局，广东 广州 510663；2.中国电力工程顾问集团 中南电力设计院有限公司，湖北 武汉 430071；3.大连理工大学 海洋科学与技术学院，辽宁 盘锦 124221)

0 引 言

海底电缆是将海上风机发电、海洋潮汐能等海上新能源运输至陆地使用的唯一通道，其重要作用不可替代。由于海床的土壤特质不均匀，加上海浪的长期洗刷、渔船作业误捞、生物侵袭以及电缆自身老化等原因易造成海底电缆的破损甚至失效。通常情况下，水深30 m以内发生海底电缆故障时，施工方常采用潜水员下潜抢修的方法。但其缺点十分明显，当水深超过50 m时，潜水员无法正常作业。在这种情况下，水下机器人可代替人工，携带多种设备下潜至海床进行工作。由于海底地面是非结构化环境，不仅有大量的松软区域，而且有很多海底障碍，因此机器人需具备较好的运动性能和较强的环境适应能力。海床和滩涂的土壤较稀软，其抗压强度和抗剪强度较低，导致海底作业装备在海床和滩涂上行走时的沉陷量增大、滑移量增大。

目前在解决通过提高接地面积来提高机器人作业能力的研究尚少，大多数对于改变履带机接地面积的研究可以总结为两个接地面积模式。通过结构变化使接地面积发生改变，这种变化方式单一，只能适应两种作业力工况。为了实现履带机的全工况适应性，针对接地面积的实时变化进行研究，设计一种可以实时改变接地面积的履带作业机器人，并分析实时改变接地面积是否对履带机的作业力有所提升，并通过合适的方式保证履带机的履带长度在结构变化过程中保持不变，以保证设计的合理性。

1 国内外研究现状

可重构履带结构是指根据不同的应用需求，改变自身的体系结构，以使每个特定的应用需求提供与之相匹配的体系结构，即可重构的体系结构。

1.1 国内研究现状

通常可重构式履带机可分为轮履结合式、连杆式等。轮履式结构较多，文献[1]提到某高校于 2018 年设计一种多运动态可重构轮履复合式机器人，该机器人的履带底盘机构具有轮式、履带式和翻转式等 3 种运动模式，可根据不同的作业需求转换工作模式。LUO等[2]与RAJA等[3]设计的轮履结合式履带机器人以及张硕等[4]研究的轮履结合式机器人，通过连杆加轮系结合方式，使其能够同时切换轮子和履带的不同工作模式，满足在不同环境下作业的能力。刘肖雅[5]和张明路等[6]在轮履结合上提出新的设想，与之前通行轮的内部结构变化不同，通过设计改变整车的结构变化实现轮履工作模式的切换，可提高履带车辆的通行性，以避免轮和轮之间的空隙卡住异物。

刘万聪[7]设计一种使用铰链六杆机构达到自适应变形能力的履带式机器人，可重构式变形机构通过改变机器人前导轮的角度和高度增加履带机的越障能力以及对全地形的适应能力，该机器人后端的摆臂模块使用差动齿轮装置与其主履带进行连接，可起到调整质心位置、辅助支撑、越障的作用。这种移动变形机构不仅降低对驱动的性能需求，而且简化机器人的控制难度，使履带机能够以最优的结构穿过复杂路面。国防科技大学基于四连杆机构设计一种新型可重构式履带机器人 RTMbot。该履带机器人四连杆机构由悬架、驱动曲柄、从动曲柄和连杆组成可重构履带模块机器人，具有良好的灵活性。在其结构变化过程中，对电机的需求数量较多，导致控制难度增加，而接地面积的改变取决于曲柄的长度，曲柄过长易致结构的不稳定性增加，在解决接地面积的结构选择上并不是最优解。

1.2 国外研究现状

国外对于海底可重构式履带机器人的研究多集中在摆臂机器人的结构设计及分析上。日本 JAMSTEC 的团队设计一种四摆臂式履带式底盘遥控无人潜水器(Remote Operated Vehicle，ROV)[8]，该样机的摆臂可以围绕轴旋转，有效提高其全地形通过能力，同时也可调整ROV的行走和作业姿态。在浅海中，摆臂履带式 ROV 可在 30°倾角的斜坡上稳定行走。类似的设计还有美国 iRobot 公司设计的一种摆臂机器人[9]，摆臂结构解决的问题主要在越障方面，由于浅海海底较为平坦，越障并不作为考虑重点，以摆臂式为核心设计一种机器人，可以即时改变接地面积增大牵引力，以满足履带机在不同工作环境下的工作需求。

2 机构设计

可重构式履带机包括作业机主体舱、可重构式履带底盘机构和相关电子设备等3个部分。可重构式机构主要由履带底盘中的变形机构、补偿机构及基于椭圆原理设计的轮系机构共同组成，通过机构之间的变化达到能够适应不同土壤环境的目的。

2.1 基于椭圆原理设计的轮系机构

该机构的原理是指随摆臂摆动的同时，构成以驱动轮、从动轮的中心为焦点，转动轴为椭圆长轴时刻转动的椭圆。保证椭圆原理时刻存在于结构变化中。基于上述原理对履带机进行的轮系设计能够始终使摆臂轮的中心位于以驱动轮、从动轮的中心为焦点的椭圆轨迹上，确保履带始终处于张紧状态，如图1所示，保证可重构式履带机正常运行。

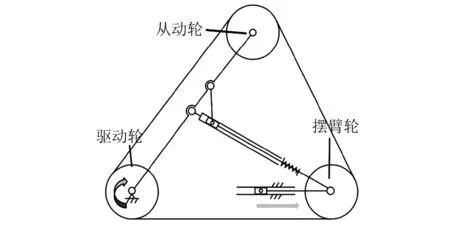
图1 可重构式履带机简图

2.2 变形机构设计

变形机构主要由电动推杆和摆臂轮组成。变形机构的变形原理是指可通过导轨中的电动推杆使底部摆臂轮外推实现其内部结构的变化，实现可重构式履带机的接地面积变化。可以根据不同土壤的性质，改变履带机的底部履带长度，确定最适合的履带接地面积，避免沉陷量过大，保证履带机最大牵引力运动[10-11]。其结构变化的驱动方式由转动变为移动，降低控制难度，满足驱动的性能需求。

2.3 补偿机构设计

补偿机构主要由补偿杆、弹簧组成，使摆臂在摆动过程中摆臂的长度有所增加，实现对理论摆臂长度的增加。对于弹簧杆部分，需改变其长度进而降低对此部分的依附性，增加履带机变形过程中的稳定性。

弹簧的作用：可通过张紧作用使滑动连杆的实际长度与理论长度相同，弥补补偿机构造成的滑动连杆长度逐渐变大的影响。补偿机构增加整个机构的稳定性，便于履带机在海底更稳定地工作。

3 力学分析

3.1 力学模型分析

对履带机进行受力分析，建立装备在运动状态下沿竖直和法向两个方向的二自由度力学模型，分析装备在作业状态下法向产生的沉陷量和水平方向的牵引力变化。通过受力分析对装备整体结构参数进行设计。由于法向和竖直方向的受力变化是耦合的，无法通过单独分析进行求解，需要充分找到各参量之间的变化关系，才能使装备设计更加合理。

3.1.1 竖直方向力学模型分析

履带机在海底工作时需通过浮力模块改变对海底土壤产生的接地比压。相比于陆地而言，水下装备在竖直方向上需考虑其浮力对法向载荷的影响。如图2和图3所示，在海底工作时由于履带机排开水的体积较大，会导致其受到较大的浮力，在海底受到的纵向合力会远小于其在陆地所受的纵向合力。图2和图3中：F支为陆地或海床对履带机的支持力；G为履带机所受重力；F浮为履带机在海底所受到的浮力。

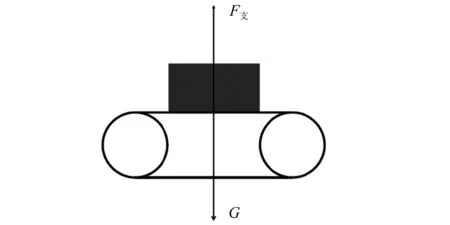
图2 履带机在陆地上的纵向力分析

图3 履带机在海床上的纵向力分析

履带在陆地上所受的力可表示为

F支=G

(1)

履带在海底所受的力可表示为

F支+F浮=G

(2)

(3)

式(3)中：P为接地比压；B为履带宽度；L为履带接地长度。

履带的驱动力由剪切地面而产生，其最大驱动力由地面的剪切强度和接地面积确定：

Fmax=Ac+Wtanφ

(4)

式中：A为履带的接地面积；c为地面的表现内聚力；W为法向压力；φ为内剪切阻力角。

履带机纵向的合力对履带机的牵引力有所影响，在研究中设定履带机在海底工作时的纵向合力为5 kN。

3.1.2 水平方向力学模型分析

与竖直方向相比，履带机水平方向受力复杂，包括牵引力、作业力、推土阻力、压土阻力、海水阻力、坡度阻力、加速度阻力、摩擦阻力等。为简化分析过程，仅考虑履带机的牵引力、作业力和土壤阻力。履带机水平方向受力分析如图4所示。

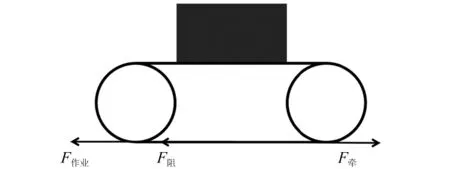
图4 履带机水平方向受力分析

F作业+F阻=F牵

(5)

式中：F牵为履带机的牵引力；F作业为履带机在工作时产生的拉力；F阻为履带机在工作时所受到的阻力，其中包括推土阻力及压土阻力。

推土阻力Rc计算如下：

(6)

式中：kc为沉积物黏聚力变形模量；b为履带板宽度；kφ为沉积物内摩擦角变形模量；n为沉积物变形系数；z为沉陷量。

压土阻力Rp计算如下：

Rp=pcosθ

(7)

式中：p为海底土壤所受压强；θ为履带车与地面夹角。

基于莫尔-库伦(Mohr-Coulomb)剪切理论和Rankine被动土压力理论，建立履带单板与土壤之间的作用关系。牵引力主要依靠履带板与土壤之间的相互摩擦影响，考虑在进行作业过程中滑移率的影响，计算牵引力的公式为

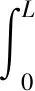
(8)

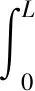
(9)

式(8)和式(9)中：F1为履带板部分剪切土壤产生的推力；C为土壤黏聚力；φ为土壤内摩擦角；j为滑转率；k为土体剪切模量。

3.2 接地面积理论分析

3.2.1 贝克模型理论

贝克模型理论[12-13]是贝克借鉴土木工程学科的公式推导在承载面最小宽度下的垂直载荷-土壤沉陷量的关系式。为了测定土壤参数，贝克研制相应的贝氏仪。贝氏仪如图5所示。

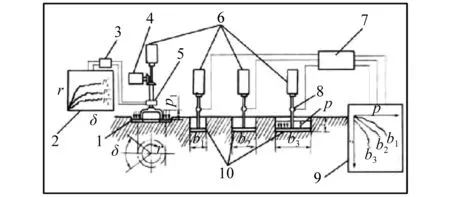
注：1.剪切环；2.记录带Ι；3.放大器Ι；4.转矩电机；5.转矩及角运动传感器；6.加载缸筒；7.放大器Ⅱ；8.压力表；9.记录带Ⅱ；10.穿入平板

贝克模型的原理是对车辆与土壤的相互作用进行力学分析，通过试验测定适当的土壤性质推导车辆和土壤参数的简化方程式。贝克进行大量的平板压力沉陷试验后得出土壤表层的压力沉陷关系为

(10)

3.2.2 接地面积理论设计

通过之前的研究可以得到作业力为

(11)

(12)

通过表1内数据可以确定辽东湾北部浅海地区土壤的含水量取值范围，根据该范围选取两种典型土壤作为研究对象，其中Hanamoto的含水量为32%。

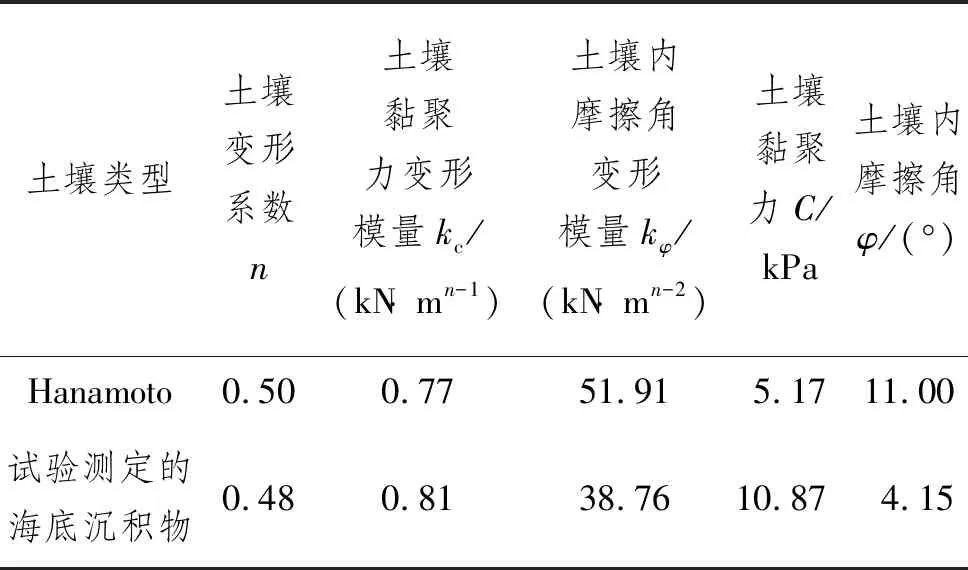
表1 辽东湾北部浅海地区土壤地质特征

根据之前总结的作业力与沉陷量之间的关系式，采用MATLAB分析该函数关系，得到接地面积与作业力分别与沉陷量之间的关系，如图6和图7所示。

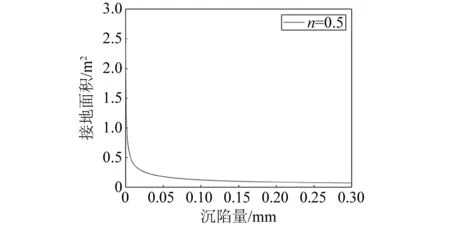
图6 Hanamoto接地面积与沉陷量关系

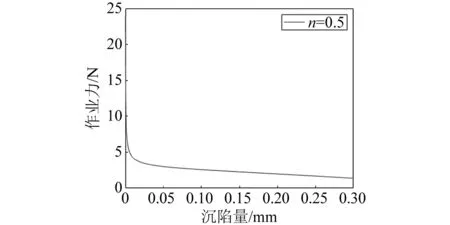
图7 Hanamoto作业力与沉陷量关系

通过图6可以选定土壤下履带接地长度，该长度确定为所设计的可重构式履带底盘机构的初始接地长度。确定最小接地面积之后，在预期设计的接地面积增大60%的情况下，可以确定作业力理论上增加约1.1 kN，作业力增加约44%。使用相同方法对上海交通大学试验测定的海底沉积物进行分析，如图8所示。

图8 上海交通大学试验测定的海底沉积物作业力与沉陷量关系

由图8可知：在履带接地面积增大60%的过程中，其作业力增加2.561 kN，增加约55%。对履带机建立履带-土壤力学模型，并通过MATLAB对履带机的最佳接地面积范围进行分析设计，得到履带机设计中的履带最小接地长度为0.9 m。

4 建模与仿真分析

4.1 整车模型建立

通过SolidWorks2020建立履带机整车模型。在建模过程中，考虑在一个装配图中过多的零件会导致软件发生卡顿，因此将履带机整机拆分，分别建模并装配到一起。履带机建模分为两个部分：履带机主体舱和履带底盘机构。建模的重点在于履带底盘机构，其建模思路如图9所示。

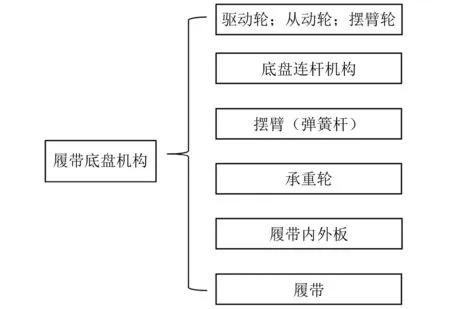
图9 履带底盘机构建模思路

通过 SolidWorks 对重要零件进行建模。图10为履带机的驱动轮、从动轮。图11为履带机的摆臂弹簧杆。

图10 履带机驱动轮与从动轮模型

图11 摆臂弹簧杆模型

通过 SolidWorks 建模后可以得到履带机的三维模型，如图12所示。履带机的内部组成包括电机、电动推杆以及电池等，如图13所示。

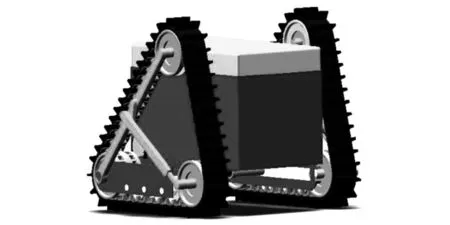
图12 履带机整机模型

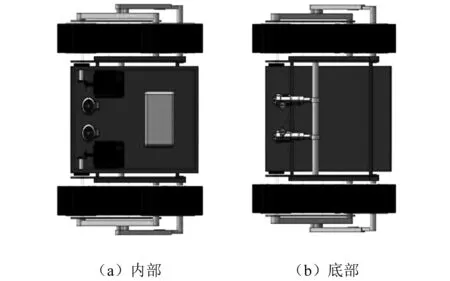
图13 履带机内部配置及底部配置

4.2 运动学仿真分析

通过 ADAMS与SolidWorks对机构进行运动学分析，设定电动推杆的进给速度为10 mm/s，可以确定固定杆、补偿杆和摆动导轨的角速度，以及弹簧杆在摆臂导轨内的线性位移随时间的关系，如图14～图18所示。

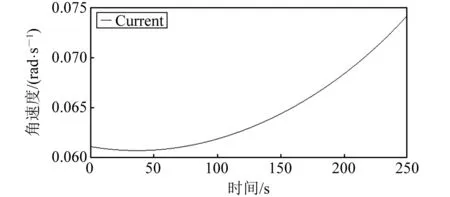
图14 固定杆角速度

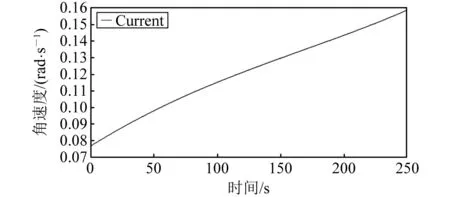
图15 补偿杆角速度

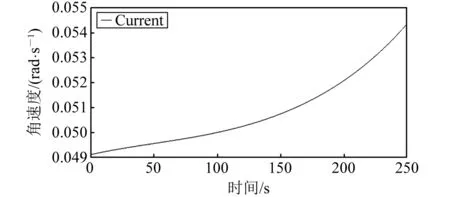
图16 摆动导轨角速度

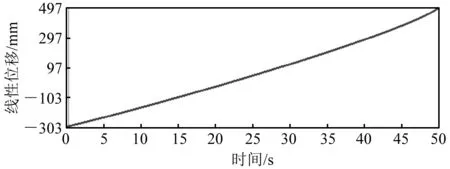
图17 弹簧杆在摆臂导轨内的线性位移

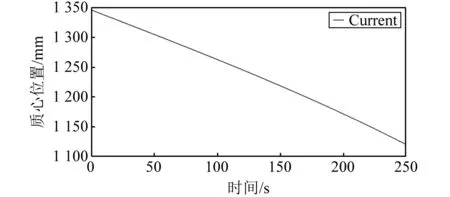
图18 从动轮的质心位置变化

由上述模拟运动仿真结果可知：在电动推杆的进给速度不变的情况下，履带机发生可重构变形的过程中，固定杆、补偿杆和摆动导轨的角速度变化平缓，弹簧杆的线性位移随时间线性变化，从动轮的质心缓慢下降。履带机的整体及各结构运行稳定，设计方案具有一定的实际意义和实用性。

5 结 论

(1)通过增大履带的接地面积，可重构式履带机能够更好地适应各种土壤环境；补偿杆及弹簧的补偿作用使履带机在运行过程中保证稳定性。

(2)分析可重构式履带机的所受作业力，利用贝克模型等理论分析其沉陷量、接地面积及所受力的关系，得到合适的履带接触面积。

(3)利用 SolidWorks 软件对可重构力履带机进行运动学仿真，分析在电动推杆进给速度不变的情况下电动推杆的推程与机构内部杆件的摆动角速度及位移的关系。

(4)利用ADAMS软件对所建的可重构式履带机模型建立虚拟样机，对履带机构内部进行动力学分析。所设计的可重构式履带机可以实现不同土壤环境下的相同作业力需求以及相同土壤环境下的不同作业力需求。