船舶肋骨线型高精度拟合方法

王 旭, 顾 胜, 张丽妮, 巫江祥, 何志伟, 刘 营, 芦 帅, 钱 华

(1.上海船舶工艺研究所，上 海200032；2.大连船舶重工集团设计研究院有限公司，辽宁 大连 116005；3.上海中船临港船舶装备有限公司，上海201306；4.上海外高桥造船海洋工程有限公司，上海201306)

0 引 言

船体、甲板所受的弯曲力会传递至肋骨上，承载能力取决于肋骨和船体之间的焊接情况，这就要求肋骨的线型需尽可能贴合船体外形。在数控肋骨冷弯机的帮助下，能够按照船厂要求的肋骨线型弯制高精度的肋骨[1]。肋骨冷弯工艺一般分为4步：①船厂提供肋骨线型数据文本，其中包含肋骨需要经过的点以及各点的曲率半径，每根肋骨的点数一般在十多个或者数十个；②将肋骨线型数据文本输入前处理软件中，拟合一条完整的肋骨线型；③根据检测距离S0、甩头(荒料)长度以及分割数n，利用弦线法[2]求解该肋骨的理论加工控制量L与θ(L为肋骨弯制点的弦长，θ为角度)；④将L与θ输入上位机，作为传感器的参考量，进行肋骨自动冷弯工作[3]。其中，第2步的线型拟合工作至关重要，高精度的拟合结果会产生高精度的L与θ，从而提高肋骨数控冷弯的精度。

传统的线型拟合方法：假设整根肋骨线型是一条三次曲线Y=aX3+bX2+cX+d，其中，a、b、c、d是待求解的参数；根据船厂给出的点，利用最小二乘法求解a、b、c、d的最优值。该方法的主要缺陷：①已知条件的数量(十多个或者数十个)远大于待求解参数的数量(4个)，因此最终拟合的三次曲线无法严格经过全部的给定点；②由于①的缘故，需要额外的误差分析，但误差的许可范围一直没有理论依据；③在拟合过程中，未考虑船厂给定的曲率半径，这会降低拟合结果的可靠性。

提出一种新型的肋骨线型拟合方法：将整根肋骨线型看成多段的分段三次函数，每一段肋骨的已知条件数目为4个(两端点的位置和两端点的曲率半径)，正好等于三次曲线的系数数量，使参数解静定。由于考虑曲率半径，因此会使方程组非线性，提出将参数降维以及坐标系局部化，可解决非线性方程的高精度求解问题。

1 船舶肋骨线型拟合数学模型

1.1 已知条件

由厂方提供肋骨线型数据的ASCII文本文件和与之对应的肋骨加工参数的ASCII文本文件，后者包含该肋骨的关键数据，其构成如图1所示，其中，点数为该肋骨上给定点的数量。由图1可知：数据文本不仅给出每个点需要经过的坐标X和Y，而且给出每个点对应的曲率半径。

图1 肋骨线型数据文本内容构成

1.2 任务分析

根据已知条件，船舶肋骨线型拟合需解决的基本问题：已知平面内点Pi(Xi，Yi，R)和与其相邻的点Pi+1(Xi+1，Yi+1，Ri+1)，其中，i=1，2，…，N-1；拟合一条平面曲线Y=fi(X)，其中，fi的下标“i”表示该曲线在Pi与Pi+1之间。该曲线需满足下式：

(1)

式中：ri为fi的曲率半径。

ri表达式[4]为

(2)

式中：d和d2分别为对fi的一次微分和二次微分。

1.3 求解模型

由式(1)可知：Pi与Pi+1总共提供4个已知条件，因此fi中待求解的参数也设置为4个，这样可使方程组的解静定。为使fi可二次微分(如此，曲率半径才有意义)，指定fi为三次曲线，即fi满足下式的形式：

fi(X)=aiX3+biX2+ciX+di

(3)

一般来说，数值优化均需要事先指定初始搜索值，如果指定的初值不合适，则易陷入局部最优解[5]，甚至错误最优解。对于设计人员来说，ai、bi、ci和di的取值范围过于宽泛，均在(-∞，+∞)之间，如何指定合适的初值没有准则，因此不建议直接对ai、bi、ci和di进行求解，可利用坐标系转换进行降维处理。

1.4 降维处理

肋骨曲线数值拟合模型如图2所示，其中，Pi、Pi+1和Pi+2均为已知条件中的给定点，其坐标值均在全局坐标系OXY下表示。如果直接在OXY下进行曲线fi的拟合，缺点如下：①如第1.3节所述，无法指定合适的ai、bi、ci和di的初值，优化结果不可靠，甚至错误；②在OXY下，Pi、Pi+1和Pi+2的坐标值一般均较大，数量级一般为“千”或者“万”，影响求解精度。

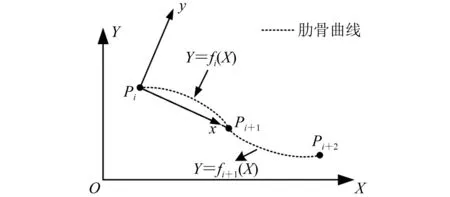
图2 肋骨曲线数值拟合模型

基于上述缺点，建立以Pi为原点、PiPi+1为x方向的局部坐标系Pixy，其中，y方向是x绕着Pi旋转90°所得(旋转方向为纸面向外)。在Pixy下，Pi坐标为(0，0)，Pi+1坐标为(L，0)，其中，Li为Pi与Pi+1之间的距离，一般数量级为“百”。在Pixy下，肋骨曲线不再是Y=fi(X)，而是y=gi(x)，如图3所示。只要求解出g，肋骨曲线即可确定。

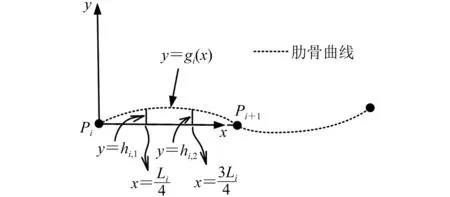
图3 在局部坐标系下拟合肋骨曲线

曲线gi是三次曲线，按下式计算：

gi(x)=pix3+qix2+six+ti

(4)

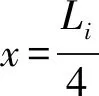
(5)

当hi，1和hi，2确定之后，代入式(5)可解出pi、qi、si和ti，曲线gi可确定[6]，即可计算gi在Pi与Pi+1处的曲率半径。对于同一条曲线，曲率半径的值与坐标系无关[7](曲率半径的几何性质)，因此，在OXY下，Y=fi(X)在Pi与Pi+1处的曲率半径即可求得，将结果与要求的曲率半径Ri、Ri+1计算差值，作为优化的目标函数。

综上所述，将肋骨线型的优化问题从优化ai、bi、ci和di这4个参数转换为优化hi，1和hi，2这2个参数，实现降维。接下来的关键问题在于hi，1和hi，2的初值如何选取，需要结合船舶肋骨曲线曲率半径大的特点。

1.5 初值选取

由图3可知：当hi，1和hi，2均为0时，gi为一条直线，曲率半径为无穷大；当hi，1和hi，2逐渐从0变大时(+y方向变大或者-y方向变大)，gi为一条有弯度的曲线，此时gi在Pi与Pi+1处的曲率半径逐渐由大变小。考虑船舶肋骨曲线曲率半径大的特点，可将hi，1和hi，2的初值定义为±0.01，具体的正负号根据表1确定，其中，Ri与Ri+1的正负号符合右手螺旋定则(绕着纸面向外)。

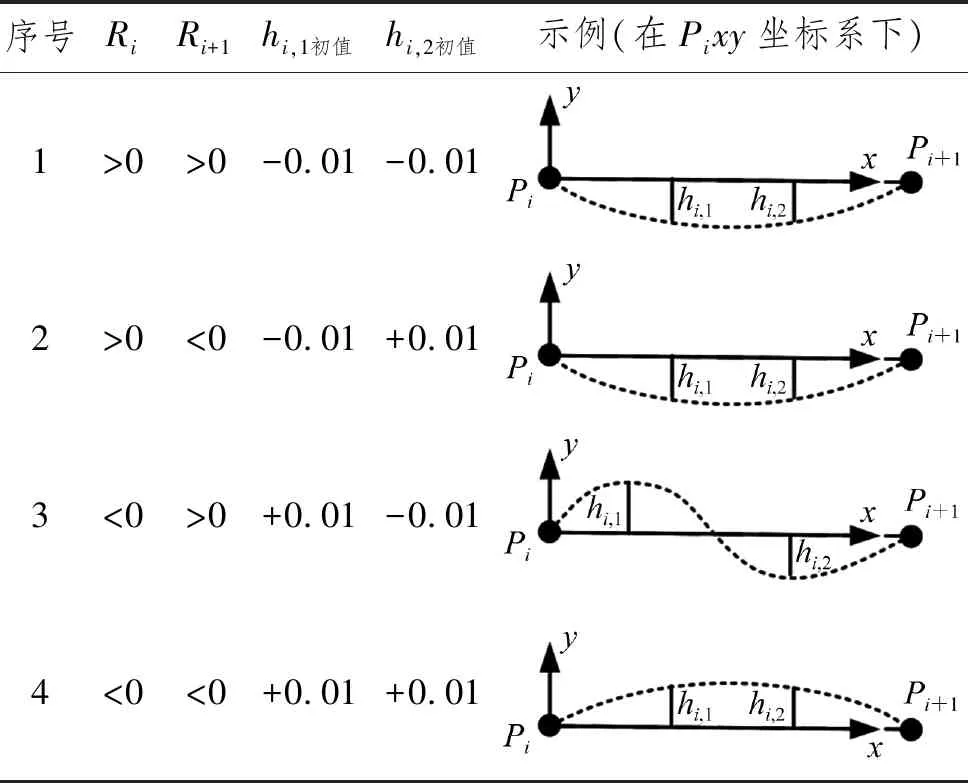
表1 hi，1和hi，2的初值定义

根据表1，可总结hi，1和hi，2的初值选取公式：

(6)

式中：sign为求正负号。以此初值，代入相关优化算法，求出符合要求的hi，1和hi，2，即可求出肋骨曲线在局部坐标系Pixy下的表达式。

下一步需要将坐标系Pixy下的表达式转换回原始坐标系下，即全局坐标系OXY下。

2 坐标转换

坐标转换如图4所示。

图4 坐标转换示例

假设在经过第1节的操作之后，获取坐标系

Pixy下Pi与Pi+1之间的曲线方程gi，则在gi上任取一点(xm，ym)∈g，则该点在全局坐标系OXY下的坐标值(Xm，Ym)计算公式[8]为

(7)

式中：Rθi，z为绕z轴(即纸面向外)旋转θi角度对应的旋转矩阵是2×2维。

(8)

式中：θi为X绕z轴(即纸面向外)旋转θi角度后到达x。

θi的表达式为

(9)

式中：X=[1，0]；x=[Xi+1-Xi，Yi+1-Yi]；“·”为向量内积；“‖‖”为向量模长。

3 整体算法

将第1节与第2节的算法整合，可得到Pi与Pi+1之间的肋骨曲线拟合算法，流程如图5所示，其中，优化算法一般分为置信域方法[9](Trust-region Methods)和最小二乘(Levenberg-Marquardt)法[10]。该流程最终输出的是在全局坐标系OXY下拟合的Pi与Pi+1之间的肋骨曲线离散点数据(Xm，Ym)∈fi。

图5 肋骨曲线拟合算法流程

以此类推，其余相邻点之间的肋骨曲线的离散点数据均可获得，最后得到的肋骨曲线满足两个条件：①严格经过已知条件中给定的所有X、Y值；②曲率半径以高精度逼近已知条件中给定的所有R值。

4 数值实例

4.1 相邻点之间的曲线拟合算例

指定4个点P1、P2、P3和P4，具体数值如表2所示。根据所提出的算法，可解出相邻两点之间的肋骨曲线的参数hi，1和hi，2，并求出P1、P2、P3和P4处的实际曲率半径及其误差。由表2可知：曲率半径误差数量级为10-5，精度较高。

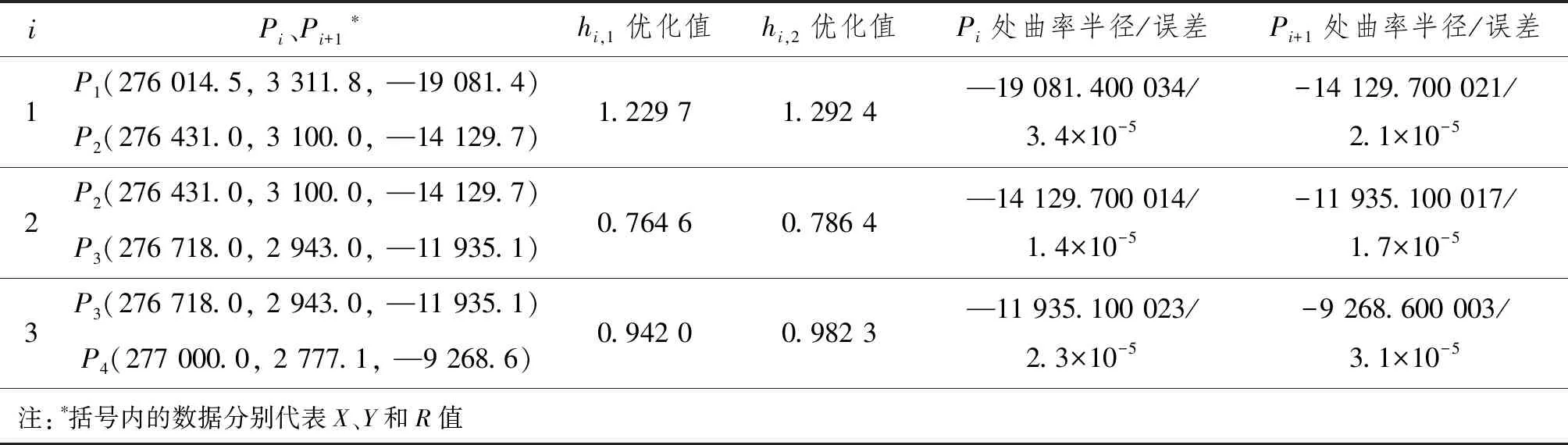
表2 相邻点之间的曲线拟合算例结果汇总

在全局坐标系OXY下，用拟合后的离散点数据绘制P1、P2、P3和P4之间的肋骨曲线，如图6所示。由图6可知：共3段肋骨曲线，每段肋骨均平滑，且段与段之间衔接处也光滑。整条曲线看似直线，原因在于X、Y轴是等比例绘制，且曲率半径较大。

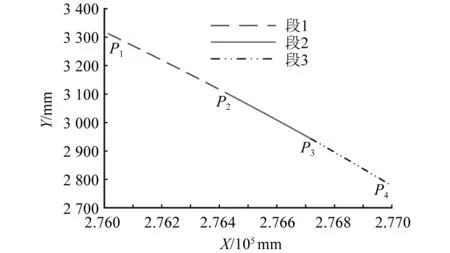
图6 拟合后的P1、P2、P3和P4之间的肋骨曲线

4.2 整根肋骨曲线拟合算例

通常在厂方提供的肋骨线型数据文本中点数均为十多个甚至数十个，为显示所提出算法的有效性，选取4根肋骨的线型数据文本，分别拟合，得到在全局坐标系下的曲线结果，如图7～图10所示。所提出的算法可以处理各种类型的肋骨数据，包括单向曲率和双向曲率(即S型)，且拟合后的曲线处平滑，曲率半径误差较小(数量级为10-5)，接近零值。

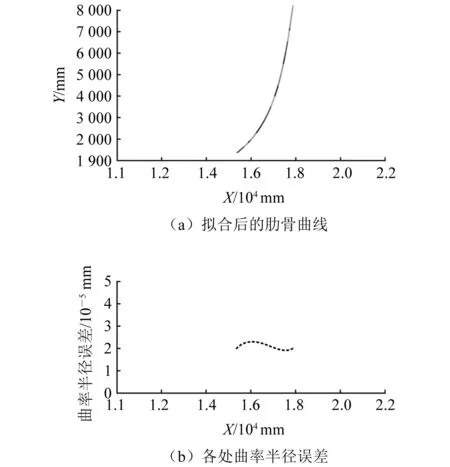
图7 右舷朝艏(单向曲率)肋骨拟合结果

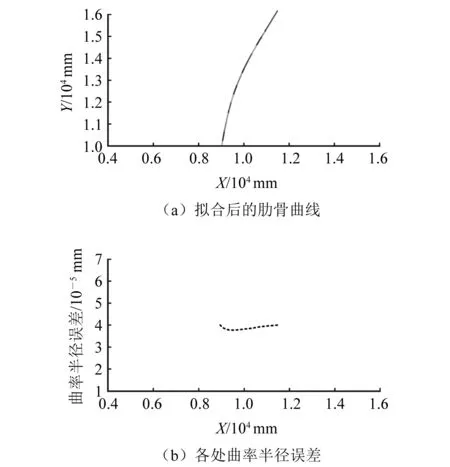
图8 右舷朝艉(单向曲率)肋骨拟合结果

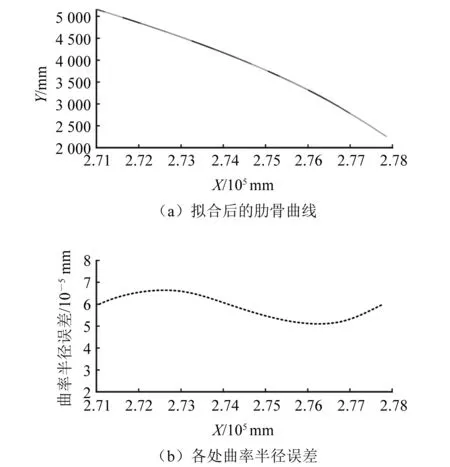
图9 右舷朝上(单向曲率)肋骨拟合结果

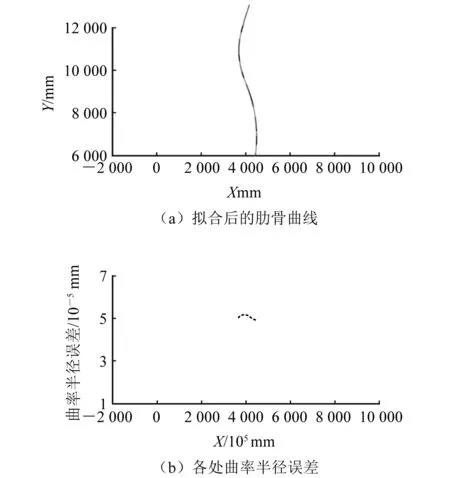
图10 右舷朝艏(双向曲率S型)肋骨拟合结果

5 结 语

随着船舶行业的结构调整转型，造船技术向自动化、智能化水平发展，目前各大船厂现存的程控肋骨冷弯机迫切需要升级改造成数控肋骨冷弯机，而目前数控肋骨冷弯机上位机程序匹配的硬件已停产，因此开发新的数控系统可以为扩大数控冷弯机市场并持续发展提供支撑。在数控系统中，针对船舶肋骨线型的高精度拟合是关键步骤。对旧的拟合算法进行改进，使数控系统获得更高精度的输入(即理论加工控制量L与θ)，以期提高肋骨自动冷弯的质量。主要研究工作如下：

(1)将整根船舶肋骨看成多个分段，每个分段是独立的三次曲线。

(2)在每个分段建立局部坐标系，在局部坐标系下，将三次曲线需要求解的4个参数减少为2个。

(3)在局部坐标系下，根据肋骨曲率半径大的特点，给出参数初始解选取方法。

(4)利用置信域方法或最小二乘法求解参数，使曲率半径的误差数量级达10-5。

(5)利用坐标变换将局部坐标系下的结果转换回全局坐标系，获得最终的高精度拟合曲线。