基于高比例电力电子的海上风电多端柔直系统的频率振荡抑制

李 欣，林继灿，王 红

(1.河北民族师范学院，河北 承德 067000；2.华南理工大学电力学院，广东 广州 510640)

0 引 言

风能是一种典型的可再生能源，其发电组合每年都在持续增长[1]。其中大型海上风电场(Offshore wind farms，OWF)具有占地面积小、风速高和年利用小时数高等优点，是可再生能源的关注领域。OWF与陆上电网的距离长，并且需要大量电力传输，因此，电压源转换器的多端高压直流(Voltage source converter-based multi-terminal high-voltage direct current，VSC-MTDC)成为海上风电场大规模集成输电的高效技术[2-3]。

高压直流输电对孤岛电网和主电网之间具有解耦效果，减弱两端系统的相互作用。但是，端口间缺乏相互支撑的能力，在发生扰动的时候，容易造成系统频率的振荡[4-8]。VSC-MTDC中电力电子换流器的渗透率高，跟网型的控制策略无法使电压源转换器(Voltage source converter，VSC)获得频率支撑，同时将交流电网分割成惯性较低的区域电网，进一步加剧了系统在发生扰动时的频率抖动[6-7]。因此，许多增加高压直流输电系统惯性和阻尼的方法被提出，为系统提供频率支撑。

文献[8-9]中提出了交互通讯的风力涡轮机的辅助频率控制回路，辅助控制器将电网频率信号转换为电压下垂控制的附加直流电压信号。当风电场侧VSC(Wind farm side VSC，WFVSC)检测到直流电压偏差，OWF将通过控制变桨和风力涡轮机中存储的动能来调整输出功率[10]。文献[11]提出了集成风电场的无通信惯性响应方案，但是它忽略了VSC站和直流网络功率损耗对系统惯性的影响，同时，随着VSC数量和传输距离的增加，将导致惯性策略作用效果变差的现象。文献[12]使用惯性仿真控制方案(Inertia emulation control scheme，INEC)为系统附加惯性功率，其惯性功率利用直流电容的吸收和释放能量的能力，改变直流线路电压。文献[13]提出了双边惯量和阻尼的方法，为两端口的直流输电系统提供快速惯性和阻尼响应。然而，上述研究关注双端柔性直流输电系统，多端高压直流输电系统中VSC之间的耦合更加复杂。

VSC-MTDC中考虑到多VSC与其他无源设备(如滤波器、变压器、线路等)之间的复杂耦合，给系统的协调控制与频率振荡抑制带来了极大的困难。为了提高VSC-MTDC的频率稳定性，许多频率支撑的方法被提出。文献[7]提出利用阻尼因子改进VSC-MTDC的惯量阻尼模拟控制方法。但是该方法无法对异步交流的互联系统实现惯量和阻尼支撑。文献[14]使用自适应下垂系数提高VSC-MTDC的动态稳定性和实现有功的分配。文献[15-16]对虚拟同步机(Virtual synchronous generator，VSG)的VSC控制方案进行了研究，使VSC具有电网支撑能力，同时具有惯性和阻尼特性。文献[4]在文献[12]的基础上，改进INEC方案，通过控制直流电压和交流电网频率来利用高压直流系统直流链路电容器中存储的电磁能量。但是，INEC方案并未模拟出[15-16]中设计的同步发电机的阻尼特性，而阻尼特性对于系统在振荡收敛中具有重要的作用。文献[17]使用有功功率/直流电压下垂控制为VSC-MTDC提供频率支撑，但是无法为系统提供惯量和阻尼响应。

在多端口直流输电区域中，海上风场区域主要由高比例电力电子接口组成，其所表现出的弱电网特性会使其在捕获的风能扰动时，容易发生较大的系统区域频率波动[18]。因此，为抑制VSC-MTDC中弱电网特性的区域发生频率波动，本文提出了一种基于VSC-MTDC的附加惯量阻尼的控制方法。利用网侧VSC(Grid side VSC，GSVSC)直流电压控制调节直流电压参考值，进而对惯性功率进行模拟，以提高系统间的惯量。同时利用系统中的频率信息构造阻尼项。有效抑制风电场侧VSC系统在发生功率扰动时引起的频率波动，加快了频率的收敛速度。最后利用电磁暂态仿真验证了方法的有效性。

1 VSC-MTDC系统结构和传统控制策略

VSC-MTDC系统的典型径向拓扑[19]如图1所示，其中，R为直流侧线路电阻，X为直流侧线路电抗。OWF的发电功率由WFVSC收集并注入VSC-MTDC系统。长海底电缆将电力传输到公共耦合点(Point of common coupling，PCC)。然后根据控制策略将功率分配给每个GSVSC。图1中，左侧OWF区域和孤岛区域为弱电网，陆上交流电网为强电网。电网强度依据其短路比(Short-circuit ratio，SCR)大小进行定义[20]，本文弱电网SCR=3，强电网SCR=10。

图1 VSC-MTDC系统

在VSC-MTDC中，WFVSC和GSVSC的控制策略如图2所示。OWF被认为是一个弱交流电网，需要WFVSC提供的电压和频率支持。通常需要锁相环进行功率控制[14]。

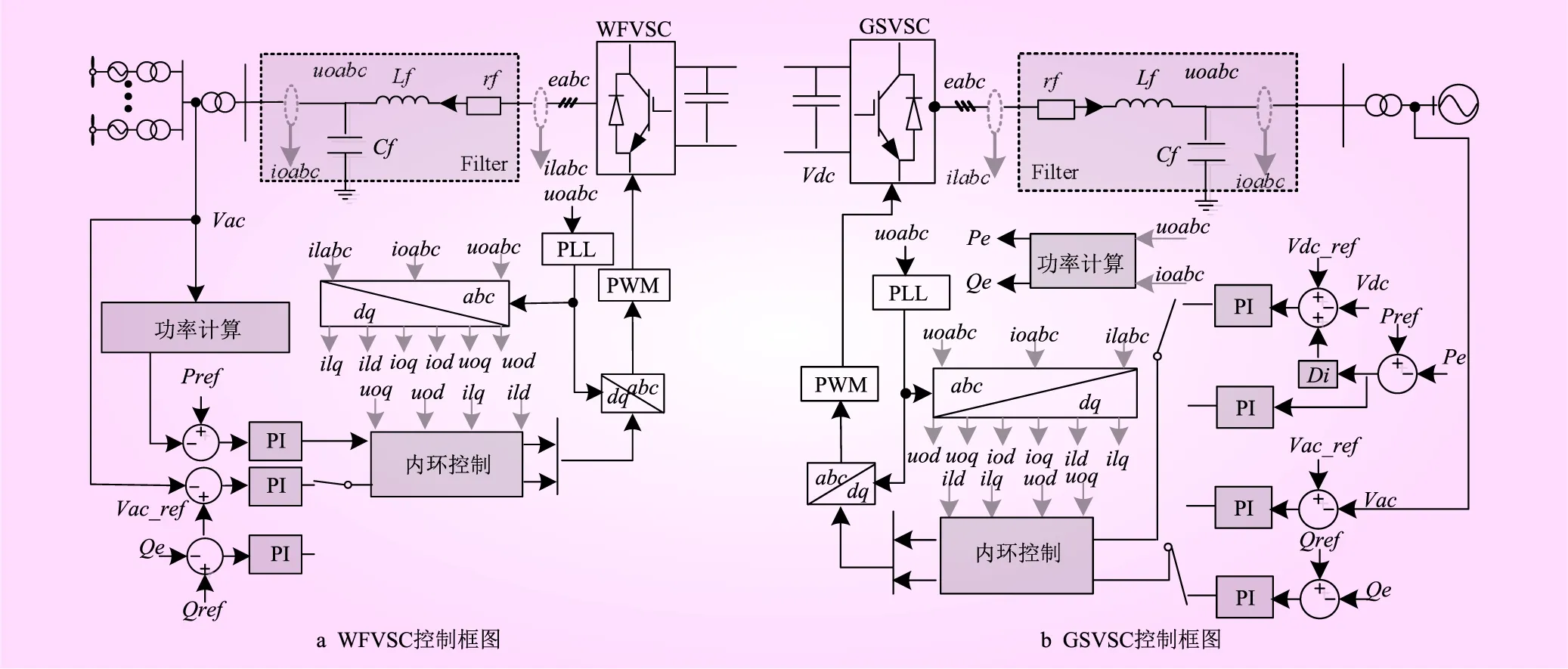
图2 VSC-MTDC控制框图

对于GSVSC，目前的研究控制中主要是使用功率控制或者功率-直流电压(Power vs. DC Voltage，P-V)下垂控制作为基本控制器[21]。

2 基于同步电机的惯量阻尼模拟

本文所提出的交互惯量阻尼方案基于同步发电机的转子运动方程，为VSC-MTDC提供惯性功率和阻尼功率，具体包括惯量模拟控制方案和阻尼模拟控制方案。

同步发电机的转子运动方程为

(1)

式中，J和D分别为转子转动惯量系数和阻尼系数；ω和ω0分别为电网角频率和额定角频率；Pm和Pe分别为同步电机输入机械功率和输出电功率。

根据功率流向，直流电容充放电控制直流侧电压值，可得

(2)

(3)

进一步积分可得

(4)

则惯量模拟方法获得的Vdc_refi可以表示为

(5)

结合式(1)和式(5)可知，模拟的惯性功率根据频率变化进行调整，同时直流侧电压具有调节功能。因此，调整直流线路中的直流侧电压，用来跟随频率的变化，向两侧提供具有转动惯量Ji的惯性功率。

由式(5)可知，直流电容的选取对于直流电压的稳定具有重要作用。因此，需要选取合理的直流电容，才能有效提供稳定的惯量功率。式(5)可以被重新表示为[7]

(6)

对其进行泰勒公式展开，忽略高阶项后可得

(7)

(8)

由式(8)可知，电容与频率和直流侧电压的变化速率有关，结合系统频率和直流侧电压变化的幅度，定义上限为

(9)

式中，右下角的min和max分别代表最大和最小偏移值。因此，直流电容的参考值可以计算为

(10)

WFVSC中，采用了功率-电压控制，因此，直流电容提供的惯性功率可以利用有功控制模拟到WFVSC中

(11)

式中，P0i为有功功率的参考值。通过式(11)可知，当OWF发生功率扰动时，WFVSC 通过改变注入有功功率进行二次调节，此部分为向WFVSC注入的惯性功率，从而使系统获得根据频率变化而模拟的惯量。结合式(5)可知，模拟的惯性功率由GSVSC 通过直流侧电压控制改变电容的电磁能，进行电压参考值的调整而获得。同样根据等式(1)可知，阻尼功率可以描述为D(ω-ω0)，只要存在角频率偏移(ω-ω0)，就会存在阻尼功率。因此，WFVSC侧模拟阻尼功率后可以描述为

(12)

由式(12)可知，在系统频率发生波动时，通过改变WFVSC的功率给定值Prefi，使其附加阻尼功率。当系统稳定时，附加的阻尼功率为0，不影响系统的稳定运行的。

3 参数稳定性分析

为了更好分析模拟的转动惯量系数和阻尼系数，利用小信号分析方法进行参数分析。具体建模过程可以参考文献[22]。线性化后的系统小信号模型可以表示为

(13)

式中，u为控制器输入；y为VSC-MTDC系统的输出量。结合图2可知，VSC1-VSC3同样为控制直流侧电压的并网模块，采用基于功率下垂的直流电压外环控制策略，VSC4和VSC5为海上风电侧模块，与VSC3同样为弱电网侧，采用功率-电压外环控制。因此，不失一般性的对(J1，D1)、(J3，D3)和(J4，D4)进行分析。增大参数，范围从0到50，其根轨迹变化如图3～5所示。

图3 J1和D1变化时根轨迹

由于系统整体阶数较高，相应的特征根也较多，因此图3～5展示了变化较为明显的部分主特征根。

由图3a、5a可知，Ji增大的时候，主特征向左边偏移幅度较大，有利于系统的稳定性；但是小部分向右偏移，因此过大的Ji值不利于系统的稳定性，同时大部分特征值变化趋势较小。其中图4a、5a中，参数变化对系统特征值变化影响更大，这是由于弱电网下，系统对于参数变化的灵敏性较高；而图3a中特征值变化趋势小，是由于强电网下，系统韧性强度高，稳定性较好。

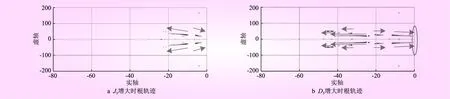
图4 J3和D3变化时根轨迹

由图3b、4b、5b可知，随着Di的增大，系统大部分主特征值向左边偏移，系统的阻尼增大，能有效抑制系统的振荡。由图4b可以看出，过大的阻尼容易使得系统在稳定附近点波动，从而导致失稳定[23]。同样，图4b和图5b中，系统主特征值变化幅度较大，这是由于弱电网侧引起整体系统的波动较为明显，因此，模拟的惯量功率和阻尼功率对系统的影响较为明显。

4 算例分析

为了验证所提出方法的有效性，使用MATLAB/Simulink软件模拟如图1所示的五端口VSC-MTDC模型，包含2个非同步陆上电网和2个OWF的网络。系统参数参考文献[14]，同时，直流侧电容的选取满足式(10)的要求。每个OWF的总风力为240 MW，GSVSC的初始功率分配比为3∶1∶2，如表1所示。

表1 MTDC的初始参数

4.1 传统控制策略

在t=4 s时，WTVSC1风能捕获功率发生扰动，此时系统功率输出以及频率输出如图6所示。

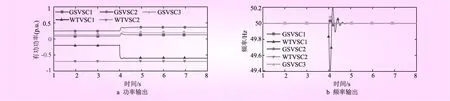
图6 传统控制策略系统输出波形

由图6可知，仅采用传统控制策略时，当WTVSC1侧发生扰动时，弱电网侧的输出频率波动比较明显。其中，由于弱电网特性，在发生扰动时，WTVSC1输出的频率振荡较大，其次是GSVSC3。当频率动态性能较差时，将严重影响系统整体稳定运行。

4.2 附加惯量和阻尼模拟控制

结合图3～5的分析，本文选取惯量系数和阻尼系数为J1=J2=J3=J4=J5=2；D1=D2=D3=D4=D5=2。

增加惯量功率和阻尼功率后的输出如图7所示。与图6相比，当VSC-MTDC采用所提出的惯量阻尼模拟方法时，GSVSC3和WTVSC1的频率波动明显减小，说明功率振荡已被深度抑制。图8为GSVSC1附加的惯性功率，图9为WTVSC1所附加的阻尼功率和惯性功率。由图8、9可知，惯性功率和阻尼功率可以根据角频率的变化而进行调整，为系统提供惯量和阻尼。

图7 附加惯量和阻尼控制策略系统输出波形

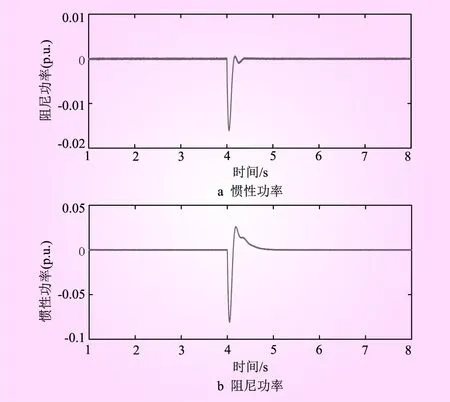
图9 WTVSC1的惯性功率和阻尼功率

4.3 考虑通讯延迟分析

由于所提的方法需要利用各端口的频率进行交互模拟惯量功率和阻尼功率，同时海上输电与陆上电网具有较长的距离，因此，需要考虑通讯延迟的工况下，算法的有效性。根据文献[24]可知，通讯延迟大约在20 ms之间。定义通讯延迟为Tc，延迟由10～1 000 ms对系统主特征根的影响如图10所示。由图10可知，随着通讯延迟的增加，主特征根往右边移动，说明系统的稳定性减低。当系统通讯在1 000 ms时，主特征根接近虚轴，系统的稳定性受到较大的影响；但是特征根同样在左半轴，证明系统在较大的通讯延迟下，系统的稳定裕度较高。

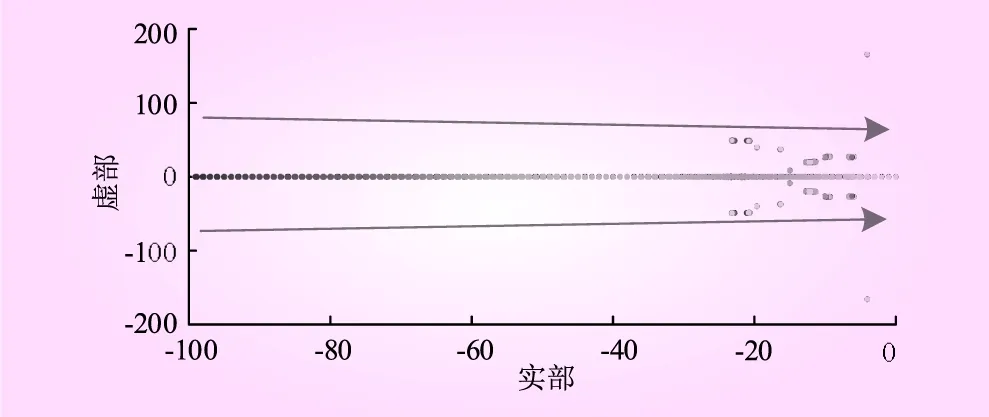
图10 Tc变化下系统主特征根变化曲线

图11为Tc=100 ms时系统输出。从图11可知，在较大的延迟环境下，算法同样有效，说明了所提方法具有较高的延迟裕度。

图11 通讯延迟下系统输出波形

5 结 论

本文研究了VSC-MTDC的惯量和阻尼模拟控制，为系统整体提供惯性功率和阻尼功率，抑制系统发生扰动时的振荡。所提的惯量和阻尼模拟方法，利用直流电容充放电能力，在弱电网区域发生功率扰动而引起频率波动时，为系统补偿惯性功率，进行多端口的频率支撑。其次，在系统频率调节期间，根据频率的变化，进行阻尼功率的模拟。所得结论如下：

(1)模拟的惯性功率和阻尼功率只需对端口的频率进行测量即可。在使用较少的频率信息交互下，所模拟的惯性功率和阻尼功率方案具有较高的延迟裕度。同时，由于所模拟的惯性功率需要利用直流侧电容的充放电能力，因此，直流侧电容的选取需参考电压和频率变化的范围进行筛选。

(2)弱电网侧系统对扰动的抑制能力较低，同时对参数的灵敏性较高，因此，所增加的策略在弱电网侧附加惯性功率和阻尼功率时，参数调整范围不宜过大。

(3)通过仿真和实验可知，与传统控制策略相比，所增加的惯量和阻尼模拟方法能有效的提高系统的动态性能，保证了风电区域交流网在受到功率波动下的系统稳定，避免了因高比例电力电子设备接入所带来功率振荡问题。