含分布式电源的配电网优化运行
彭文强
(国网湘潭供电公司,湖南 湘潭 411100)
0 引 言
配电网络重构指在满足系统约束的条件下,通过控制配电网中联络及分段开关的开、合状态,从而改变配网供电结构,达到均衡负荷、消除过载、降低网损的目的。国内外学者对此进行大量的研究,提出许多行之有效的方法[1]。
近年来,随着分布式电源(Distributed Generation,DG)的发展,越来越多DG 应用于配电网并网。大量DG 并网对线路的潮流、节点电压、网络损耗等都将产生重大影响,使配电网的运行、控制变得更加复杂,给配电网重构带来新的挑战。
为使配电网达到最佳运行状态,需依据配电网网络结构对DG 的出力进行优化控制,配电网的网络结构与DG 的出力互相关联。采用先进行配电网重构后进行DG 出力优化或先进行DG 出力优化后进行配电网重构的方式均不能使配电网运行在最优状态,需对二者同步进行优化才能达到最优状态[2]。
目前,国内外学者对含DG 的配电网优化运行研究已有一些成果。文献[3]通过分析DG 并网对配网优化运行产生的影响,对含DG 的配电网进行重构求解。文献[4]建立以网损、电压偏差以及负荷均衡协调最优的含DG 的配电网络重构模型,并提出相应求解算法。上述研究均将DG 视为恒定功率模型,未考虑DG 出力在配电网重构时的优化问题,并不能使配电系统运行在最优状况。
基于此,将DG 视为可调度设备,采用DG 出力优化调度与配电网重构相结合的二层优化模型,来处理DG 出力与网络重构之间的关系。该模型将DG 出力优化调度与配电网重构分层考虑,通过上、下层之间的信息传递与反馈,实现层与层之间的相互作用。在求解过程中,通过上下层之间的协同迭代,同步优化上下层的决策变量,逐次逼近最优解,最终实现配电网的整体优化运行。
1 配电网优化运行数学模型
1.1 优化运行目标
配电网优化运行的目标有很多,以常见的网络损耗最小为目标进行优化,表达式为
式中:i为支路编号;n为总支路数;ki表示开关分、合状态,0 代表断开,1 代表闭合;ri为支路i的电阻值;Ii为支路i的电流值。
1.2 需满足的约束条件
电压约束条件为
式中:Ui为节点i的电压;Uimin、Uimax分别为配网节点i允许的电压上下限。
支路传输功率的约束条件为
式中:Si为流过支路i上的功率;Simax为支路i允许传输的最大功率。
DG 出力约束条件为
式中:PDGi、QDGi为第i个分布式电源有功和无功出力大小;PDGimax、PDGimin为第i个分布式电源的有功出力最大、最少值;QDGimax、QDGimin分别为其无功出力上、下限。
1.3 DG 的数学模型
随着储能技术的发展,分布式电源的可调度性得到进一步增强,而传统化石能源发电及水力发电本身就具有良好的功率可调节性,调度员可对其功率进行控制。文章将可调度的分布式电源作为研究对象,视为PQ 模型。
2 二层优化模型在配网重构中的应用
分布式电源出力的配电网优化问题是一个多变量非线性组合优化问题,既需要考虑配电网结构变化,还需要考虑各分布式电源的出力情况,二者间互相影响,相互制约。这使得传统求解配电网重构的方法难以有效解决问题。
2.1 二层优化模型简介
二层优化模型是具有两层递进结构的系统优化模型,寻优的基本原理如下:首先,由上层给定下层一定的信息条件,下层按照给定的信息,根据自己的偏好或目标寻找出最佳的对策方案;其次,由下层将其对策方案信息反馈给上层,上层则依据下层反馈信息做出符合全局利益的新决策,再将新的决策信息传递给下层;最后,反复循环,直至寻找到全局最优决策[5]。在优化过程中,上层的优化决策作用于下层的约束条件,下层的优化结果以最优值的形式反馈给上层,实现层与层之间的相互作用。一般情况下,二层优化的数学模型可表示为
式(6)为上层优化模型的目标表函数,x为其决策变量;式(7)为上层优化模型的约束条件;式(8)为下层优化模型的目标函数,y为其决策变量;式(9)为下层优化模型的约束条件。上层的决策变量x作用于下层的约束条件,下层的优化结果v反过来影响着上层的目标函数。
2.2 在配电网优化运行中的具体运用
在含分布式电源的配电网优化中,为使配电网的网损最小,需要同时确定最佳的配电网网络结构和最优的分布式电源出力情况。配电网供电结构变化时,分布式电源的最佳出力方式也会发生改变。同理,当分布式电源的出力产生变化时,最佳的网络结构也在变化,二者相互制约、相互影响。为得出配网的最优运行方式,需要二者间相互递进、迭代求解。
因此,文章将配电网络结构设为上层的决策变量,将各分布式电源的出力情况设为下层的决策变量,以网损最小作为目标。采用二层优化模型对含DG 的配电网优化运行进行求解,上层决策变量给定下层确定的配电网结构,下层依据上层的网络结果,求出配网网损最小时的分布式电源的出力组合,下层再将分布式电源的出力组合反馈给上层。上层则根据反馈情况再次进行网络重构优化,产生新的上层决策变量。反复循环,直至满足终止条件。
3 模型求解
采用粒子群算法求解文章所提出的二层优化问题。上层依据网络结构特点采用二进制的粒子群算法求解,下层分布式电源出力特点采用十进制的粒子群算法进行计算。通过上下两层之间的协同迭代,同步优化二层模型中的上、下两层决策变量,求得二层优化模型的全局最优解。
4 仿真算例
为验证文章所提出方法的实用、可行性,采用常用的IEEE 33 节点配电网系统进行仿真,仿真结果如图1 所示[6]。

图1 IEEE 33 节点系统
文献[2]和文献[7]采用综合优化方法对含分布式电源的配电网进行优化分析,但都没有考虑DG在配电网中的最大接入容量。文献[2]所采用方案的DG 注入功率占总负荷的68.9%,文献[7]的DG 注入功率占比为53.2%,均不满足分布式电源总接入功率不得超过25%的规定,虽然理论上达到最优,但是缺乏实用价值[8]。基于以上问题,文章采用文献[9]的DG 接入方案,在14、18、30、33 处接入4 个DG,其中32 节点处DG 不可调,它的有功出力及无功出力分别为240 kW 和120 kvar,其余DG 的最大无功出力与无功出力分别为320 kW 和320 kvar,并设定分布式电源总输出功率小于配电网络总负荷的25%。采用不同方案对算例进行仿真,结果如表1 所示。
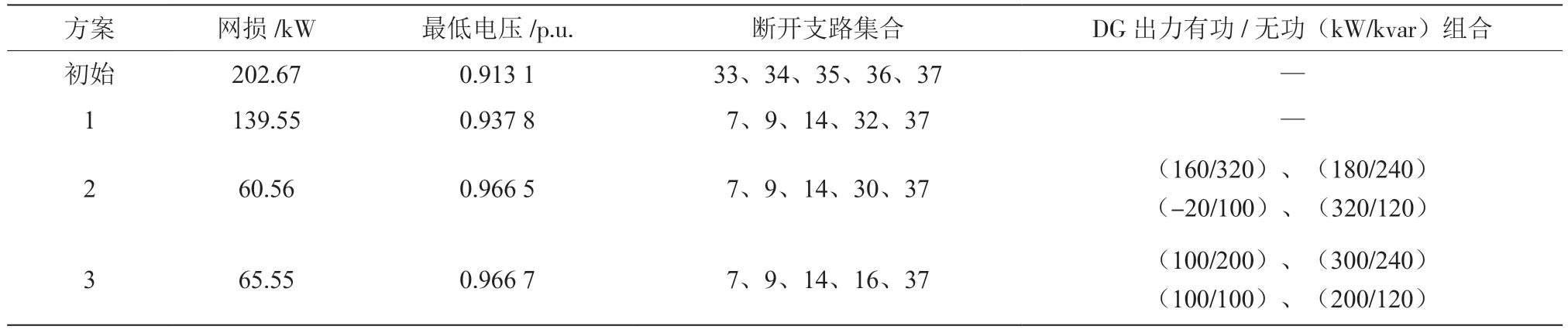
表1 重构优化结果
表1 中方案1 为不含DG 的配电网重构方案,方案2 为采用本文方法的含DG 的配电网络方案,方案3 为采用传统方法将DG 视为恒定功率模型的重构方案。
分析表1 中各方案与网络初始状况可知,通过配电网重构能大幅度降低网络损耗,提高节点供电电压,在有DG 加入的情况下,效果更加明显。表中方案2 的网损为60.56 kW,比方案3的网损65.55 kW降低了7.6%,降损幅度最大、效果最佳。由此可见,文章所采用的将DG 视为可调设备,同步优化DG 出力及配网结构的方案能使网络运行在更优的状态,相比传统的含DG 的配电网重构方法在降损方面具有明显优势。
5 结 论
为充分发挥DG 并网的作用,使配电网运行在更优状态,以含DG 的配电网作为研究对象,建立能够同时优化DG 出力及配电网网络结构的二层配电网优化模型。通过优化模型中上下两层之间的相互作用,妥善处理求解算法中DG 出力及配电网网络结构之间的关系。仿真算例结果表明,文章所提方法能够有效提高节点电压,最大限度地降低网损,在处理含DG的配电网络优化方面更符合实际且优于传统方法,对今后优化配电网络运行具有实际指导意义。

