具有遗忘个体的社会网络多维观点动力学分析与应用

刘青松 李明鹏 柴 利

近年来,社会网络分析成为网络科学研究的热点之一,吸引了来自控制科学、社会心理学和经济学等多个领域研究者的广泛关注[1-3].随着对多智能体系统[4-6]和复杂网络[7-10]研究的深入,观点动力学中观点的形成和演化引起了学者们极大的关注,产生了许多重要的结果,促进了观点动力学相关方向的发展[11-12].观点动力学的研究,不仅仅关注观点的一致现象[1],而且还关注观点的极化现象[13]和观点的分簇现象[14].例如,采用仿真分析方法,Zhang 等[15]研究了连续时间有界置信模型的观点演化问题;通过引入个人决策树和社会网络,Friedkin 等[12]分析了耦合矩阵对信念系统动力学的影响;Parsegov 等[16]在静态社会网络中,提出了一个新的观点动力学模型,并分析了观点的稳定性和收敛性.此外,Li 等[17]提出了一种新的快速、准确检测集群结构的动态方法,并且研究了电子商务系统中的动态聚类问题.

一直以来,学者们希望提出的观点动力学模型既简单又便于严格的数学分析,与此同时,又可以捕捉到丰富的社会性质.故研究者从建立优异的数学模型模拟现实世界中个体的观点演变这一根本问题出发,提出了许多经典的观点动力学模型.例如,1974 年DeGroot[1]提出了基于智能体的观点演化模型(DeGroot 模型).在DeGroot 模型中,个体通过吸收上一时刻邻居的观点形成当前时刻的观点,使得社会群体观点达成一致.然而,DeGroot 模型无法解释在良好的通讯条件下,个体观点极化的现象.为此,Friedkin 等[2]通过引入持续的外部输入(外部环境因素),提出了Friedkin-Johnsen 模型.考虑个体间相互信任的情况,Hegselmann 和Krause提出一个新的具有有界置信区间的观点动力学模型(Hegselmann-Krause (H-K)模型)[14],仿真结果表明在不同的置信区间内,观点产生一致、极化和分簇的现象[14].后来,学者们对DeGroot 模型和HK 模型等进行改进并做了较为深入的研究[18-19].

从社会心理学的角度完善观点动力学模型,以增强模型的泛化能力和应用范围,是一个值得研究的问题.1951 年Asch[20]做了一个关于因从众压力而产生观点扭曲的著名实验.基于Asch 的实验,许多学者建立了相关的观点动力学模型,并给出了严格的数学分析.例如,Javarone[21]在全连通的网络条件下,分析了从众压力对观点演化的影响,Cheng等[22]考虑了同时具有有界置信和个体压力的观点动力学模型.最近,Shang[23]研究了表达观点和私人观点的一致性问题;Ye 等[24]在社交网络是强连通的条件下,提出了具有表达观点和私人观点的社会网络模型,并分析了其收敛性.基于合作与竞争的社交网络,Lin 等[25]分析了观点的传播现象.Su 等[26]研究了噪声导致H-K 观点动力学模型拟一致性问题.

受Ye 等[24]研究强连通社会网络中观点演化问题的启发,本文研究具有遗忘个体的拟强连通社会网络中观点演化问题,并分析了观点动力学的收敛性和表达观点与私人观点之间的差异.本文主要贡献如下:

1)提出了新的具有遗忘个体的多维观点动力学模型,刻画出了不同话题之间表达/私人观点的相互影响 (详见第3 节);

2)不同于Ye 等[24]所研究的社会网络是强连通的和非周期的,且不含有遗忘个体,本文研究的社会网络是拟强连通的且含有遗忘个体;

3)应用本文提出的多维观点动力学模型,复现了“多元无知”这一经典的社会现象;

4)给出了从众压力的恢复力越小,表达观点与私人观点的差异越大这一重要结论,并且分析了逻辑矩阵对表达观点和私人观点演化的影响.

1 问题描述

本节首先介绍图论中的一些基本概念[27].设G=(V,ε,W)是一个具有加权邻接矩阵的有向图,其中,V={1,2,···,n}和ε ⊆V×V分别表示节点的集合和边的集合,非负矩阵W=[wij]∈Rn×n为加权邻接矩阵.如果存在从节点j到节点i的边,则wij＞0.如果节点i能够到达任意剩下的节点,则节点i称为根节点.如果所有节点都是根节点,则图G(W)是强连通的.如果至少存在一个根节点,则图G(W)是拟强连通的.Ni表示所有能够影响个体i的个体集合.如果则称矩阵W是行随机的(行次随机的).

定义 1[16]. 如果λi＜1,则称个体i是固执的.如果个体既不是固执的也不受任何固执个体的影响,则称为遗忘个体.

定义 2[16]. 对于矩阵A∈Rn×n,如果极限A*=limk→∞Ak存在,则称矩阵A是正则的.如果A*=1nvT,v∈Rn,则正则行随机矩阵A称为完全正则的.

本文将研究具有遗忘个体的拟强连通社会网络G(W)上观点演化问题,具体的观点动力学模型描述如下:

其中,yi(k)∈R和分别表示个体i在k时刻的私人观点和表达观点,i∈I[1,n]={1,2,···,n}.注意到,在Ye 等[24]的工作中,社会网络G(W)是强连通的和非周期的,且不含有遗忘个体.与Friedkin-Johnsen 模型[16]的本质区别是在观点动力学模型(1)中,每个个体都包含私人观点和表达观点.

在观点动力学模型(1)中,λi∈[0,1]表示个体i的私人观点受人际关系影响的敏感程度,ϕi∈[0,1]表示个体i对于从众压力的恢复程度.ϕi的值越大,则个体i所承受到的从众压力就越小,意味着个体i的表达观点和私人观点之间的差异越小.实际上,私人观点是个体的主观观点,个体根据上一时刻私人观点和上一时刻邻居的表达观点来更新当前时刻的私人观点.然而,表达观点会进行修正以符合邻居表达观点的加权平均.表示个体i分配给个体j的表达观点权重且∀i,wii≥0表示个体i对自身私人观点的自信程度.设λi∈[0,1]表示个体i对人际交互影响(邻居的表达观点)的敏感程度,1-λi则反映对于本身初始观点yi(0)的固执程度.类似于Friedkin-Johnsen 模型的“耦合关系”,令λi=1-wii.模型(1)第2 个子式的右侧表示个体i对于“本地舆论”的从众压力.假设φij≥0,且.矩阵Ψ=[φij]∈Rn×n是行随机的,“本地舆论”对于个体的影响可以通过图G(Ψ)的连通性来描述.

从众压力的形成过程并非恒定不变的,根据通讯方式的不同,个体承受从众压力的情况就会不同.例如,在较小的会议室中,无论是否存在私下交流,个体都可了解其余所有个体的表达观点.在这种情况下,所有个体的表达观点所分配的影响权重是相同的,即

然而,如果个体很多,通讯条件实际上会影响个体i对“本地舆论”的认知.例如,个体在大规模的网络空间里通过网络交流时,由于距离和通讯方式的限制,个体实际上也许无法获知部分个体的表达观点.在这种情况下,个体只能通过给定的通讯方式获取外部信息.换言之,个体通过人际影响网络认知“本地舆论”,即

注意到模型(1)的第1 个子式可写成

根据式(1)和式(2),可得

其中,矩阵Λ=diag{λ1,λ2,···,λn}和Φ=diag{ϕ1,ϕ2,···,ϕn}分别表示个体的固执程度和对从众压力的弹性恢复能力,人际网络影响矩阵,为初始的表达观点和私人观点,y(1)=(ΛW+In-Λ)y(0).

本文将研究具有遗忘个体的拟强连通社会网络G(W)中表达观点和私人观点的收敛问题 (详见第2 节).另一方面,为了描述多个相互依赖话题上表达观点和私人观点演化问题,建立了多维的观点动力学模型(详见第3 节).本文主要的研究框架如图1所示.

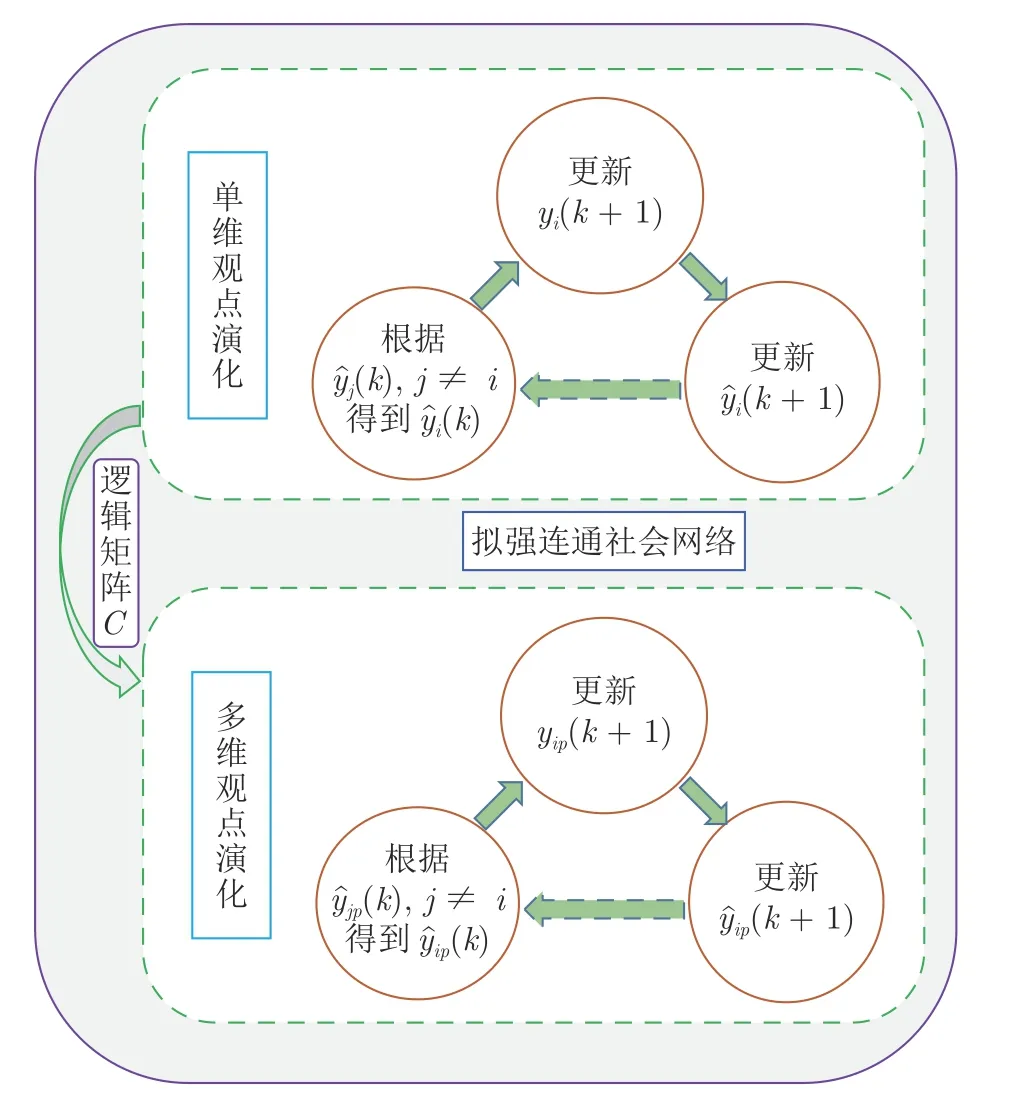
图1 本文研究框架Fig.1 The research framework of this paper

2 收敛性分析

本节将分析拟强连通社会网络G(W)中观点动力学模型(1)的收敛性.为了便于分析,将固执个体和受固执个体影响的个体编号为1 到n1(n1≤n),遗忘个体的编号则为n1+1 到n.根据定义1,易知所有遗忘个体只受邻居观点的影响(λi=1,∀i∈I[n1+1,n]).故可分解为

其中,m=n-n1为遗忘个体量,y(1)(k)∈Rn1和分别表示固执个体的私人观点和表达观点,分别表示遗忘个体的私人观点和表达观点.

不同于Ye 等[24]所提出的观点动力学模型,本文推广的观点动力学模型包含遗忘个体.显然,式(3)可改写为

显然,如果n1=n,则式(5)退化成Ye 等[24]所建立的观点动力学模型.此外,如果Ψ=W,则基于遗忘个体私人观点的观点动力学模型类似于De-Groot 动力学模型[1].

假设 1.矩阵Ψ和W是行随机的,网络G(W11)是强连通且非周期的.此外,ϕi∈(0,1),∀i∈I[1,n]和λi∈(0,1),∀i∈I[1,n1].

引理 1[24]. 对于矩阵A∈Rn×n,如果A是行次随机且不可约的,则谱半径ρ(A)＜1.

引理 2.在假设1 满足的条件下,如果社会网络G(W)中不含有遗忘个体(即n1=n),则观点动力学模型(1)是收敛的.

证明.根据Ye 等[24]的证明易知,如果社会网络G(W)中不含有遗忘个体,则易得私人观点yi(k)和表达观点都是收敛的.

定理 1.在假设1 满足的条件下,如果矩阵W22是正则的,则具有遗忘个体的社会网络G(W)中表达观点和私人观点是收敛的.

证明.首先证明具有遗忘个体且Ψ=W的观点动力学模型(1)的收敛性.

易知式(5)可写成

注意到遗忘个体的观点演化不受初始的表达观点和私人观点的影响,其演化过程类似于DeGroot 模型,即

注意到式(8)可写成

根据式(9)和式(10),可得

另一方面,由Ψ=W,可得,Ψ22=W22=.进一步地,由式(11)可得

将式(12)代入式(8)中,可得

故遗忘个体的私人观点y(2)(k)和表达观点都收敛到.注意到

由式(14)和式(15)可知,如果ρ(B)＜1,则式(16)是收敛的.

下面只需证明ρ(B)＜1.设标记从1 到n1的节点属于集合V1,剩下的节点都属于集合V2.根据网络G(W11)的连通性可知,网络G(B11)和G(B22)都是强连通的.进一步地,由于矩阵B21和B12都存在大于0 的元素,故在节点集合V1和节点集合V2中,节点之间存在双向路径.因此,网络G(B)是强连通的.

根据矩阵Λ11,,Φ11,(In1-Φ11),Ψ11都是非负矩阵,可得B≥0.由于W11和Ψ11都是行次随机矩阵,故

是行次随机矩阵,1n=[1,1,···,1]T.

根据引理1 可知,ρ(B)＜1.因此,

由Ravazzi 等[28]的命题1 可得

其中,Ω1=(I2n-P)-1.故具有遗忘个体且Ψ=的社会网络中观点是收敛的.

将定理1 与Ye 等[24]的结论比较,本文研究的社会网络G(W)是拟强连通的且含有遗忘个体,意味着观点动力学模型(1)更加符合现实情况且不需严格的通讯方式.

3 多维观点动力学分析

为了描述具有遗忘个体的社会网络中不同话题之间表达观点和私人观点的相互影响,建立如下多维观点动力学模型:

其中,yi(k)∈Rd,,i∈I[1,n],逻辑矩阵C∈Rd用于描述不同话题之间表达观点和私人观点的相互关系.yip(k)＞0.5 表示个体i的私人观点是支持话题p,yip(k)＜0.5 表示个体i的私人观点是反对话题p,yip(k)=0.5 表示个体i的私人观点是中立的,表示个体i的表达观点是支持话题p,表示个体i的表达观点是反对话题p,表示个体i的表达观点是中立的.

注意到将观点动力学模型(17)的第2 个子式代入其第1 个子式可得

类似于单维情形下的式(3),由式(18)和式(17)的第2 个子式可得

定理 2.在假设1 满足的条件下,如果逻辑矩阵C是行随机的,则不含有遗忘个体的社会网络G(W)上观点动力学模型(17)是收敛的,且收敛值为

证明.注意到

其中,⊗表示Kronecker 积.由C是行随机矩阵可得,ρ(C)=1.根据定理1 易知,当时,不含遗忘个体的观点动力学模型(17)是收敛的.设y*=limk→∞y(k)且由式(19)易知

由上式可得观点的收敛值.

当拟强连通社会网络G(W)含有遗忘个体时,在单维观点情形时,式(5)可写成式(7).类似地,在多维观点情形下有

定理 3.在假设1 满足的条件下,如果矩阵W22和C都是正则的,则具有遗忘个体的社会网络G(W)上观点动力学模型(17)是收敛的.

证明.类似于定理1 的证明,根据矩阵Ψ的结构将证明过程分为两个部分.

1)当Ψ=W时.注意到

意味着遗忘个体的私人观点和表达观点不受其余固执个体的影响.因此,由式(20)可得

由于矩阵W22和C都是正则的,可得遗忘个体的观点是收敛的,即

类似于定理1 的证明,由Ravazzi 等[28]的命题1 可知,和y(1)(k)是收敛的,故观点动力学模型(17)是收敛的.

易知,

根据Ravazzi 等[28]的命题1 可知,观点动力学模型(17)是收敛的,即由式(20)可知

其中,Ω3=(I2dn-P ⊗C)-1.

综上所述,具有遗忘个体的社会网络G(W)观点动力学模型(17)是收敛的.

本节在拟强连通社会网络中,提出新的具有遗忘个体的多维(表达和私人)观点动力学模型,刻画出不同话题之间表达/私人观点的相互影响;另一方面,本文仅需社会网络是拟强连通,意味着个体之间无需严格的通讯方式,更加符合现实社会的情景,故应用范畴取得突破.

4 仿真实验

4.1 应用于多元无知个体

应用本文所提出的多维观点动力学模型重现“多元无知”这一经典的社会现象[29].“多元无知”是指在一个个体中,只要反对意见不以明确、强烈的形式表现出来,一般成员就会产生一种错觉,以为大家的意见都是一致的.在现实中,不充分的信息交流(网络是拟强连通的)是导致“多元无知”社会现象的主要原因之一,与本文社会网络是拟强连通的条件相吻合.考虑由7 个个体组成的社会群体,其中,含有3 个遗忘个体(蓝色).网络结构如图2所示(未画出自环),其所对应的网络影响矩阵为

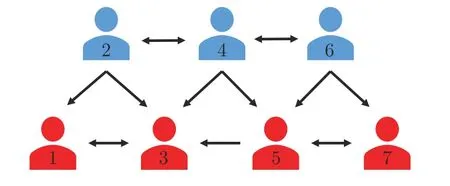
图2 具有遗忘个体的社会网络Fig.2 Social networks with oblivion individuals

以及敏感度矩阵为Λ=In-diag{wii}.设个体的初始观点为

个体恢复力参数矩阵为

易知,个体2,4 和6 是不受外界因素影响的遗忘个体,且持反对观点.根据图3 可得,个体1,3,5 和7 的表达观点从开始持支持态度演化到持反对态度,其私人观念和表达观念产生显著的差异.这是因为从众压力的影响,个体1,3,5 和7 不断修改已形成的表达观点来适应持反对态度的“本地舆论”.图3中,不同颜色的线型表示不同个体的表达/私人观点.

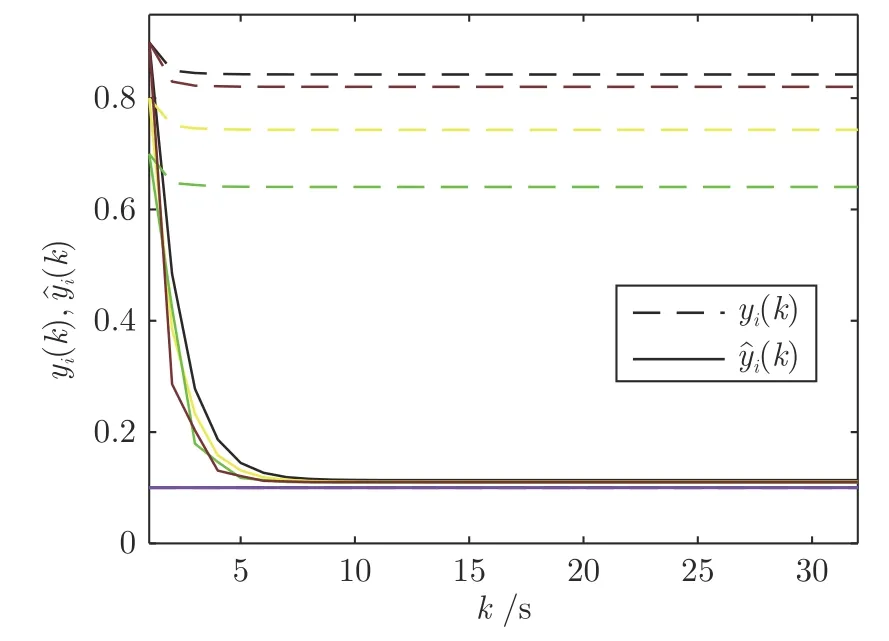
图3 多元无知Fig.3 Pluralistic ignorance

4.2 仿真分析

本节将分析逻辑矩阵C和恢复力参数ϕi对个体私人观点与表达观点之间(差异)的影响.考虑由7 个个体组成的一个网络G(W),其中,含有3 个遗忘个体(蓝色).人际影响网络结构如图4 所示(未画出自环),所对应的网络影响矩阵为

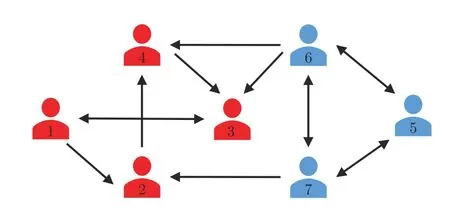
图4 具有遗忘个体的社会网络Fig.4 Social networks with oblivion individuals

以及敏感度矩阵为Λ=In-diag{wii}.根据个体数量,设定“本地舆论”包含所有个体的表达观点,即,,且

设ϕi=0.1,分别设逻辑矩阵C为

由图5～11 可知,当不同话题的观点互不影响(C=C1)时,社会网络G(W)中所有个体的私人观点和表达观点都是支持话题1,反对话题2.当C=C2时,所有个体的私人观点和表达观点都还支持话题1,但支持的态度有所减弱.所有个体的表达观点却由之前都是反对话题2 变成了支持话题2,个体1～4 的私人观点仍然反对话题2,但反对的态度有所减弱,遗忘个体5～7 的私人观点由之前都是反对话题2 演化成了支持话题2.

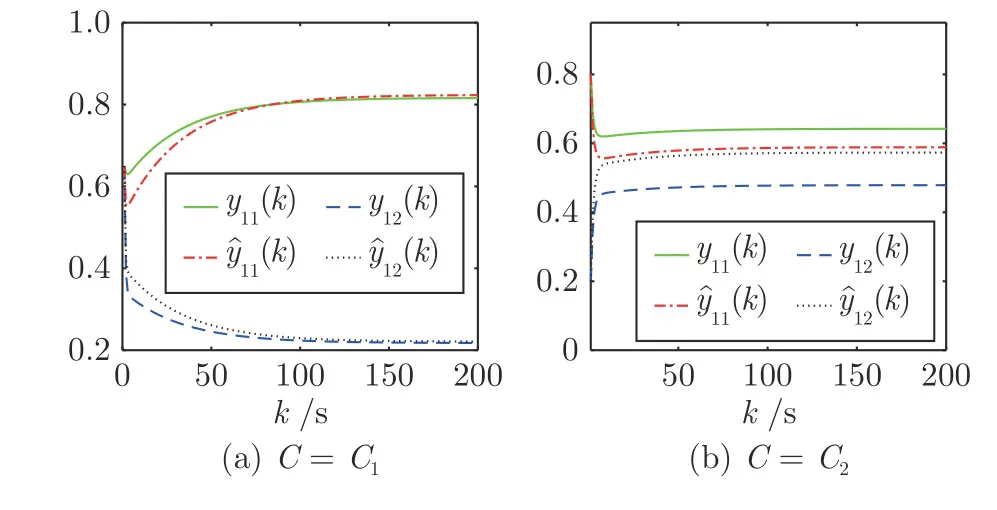
图5 个体1 的观点Fig.5 Opinions of individual 1

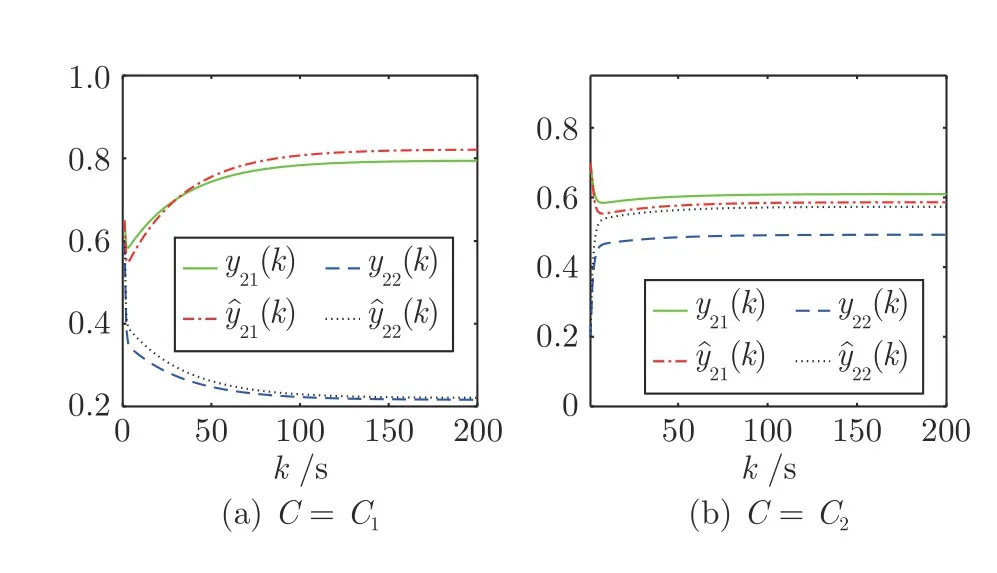
图6 个体2 的观点Fig.6 Opinions of individual 2

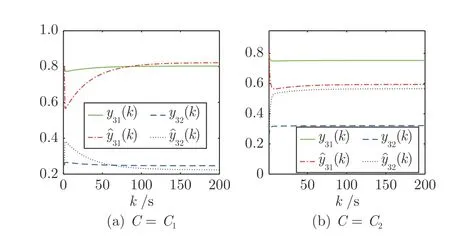
图7 个体3 的观点Fig.7 Opinions of individual 3

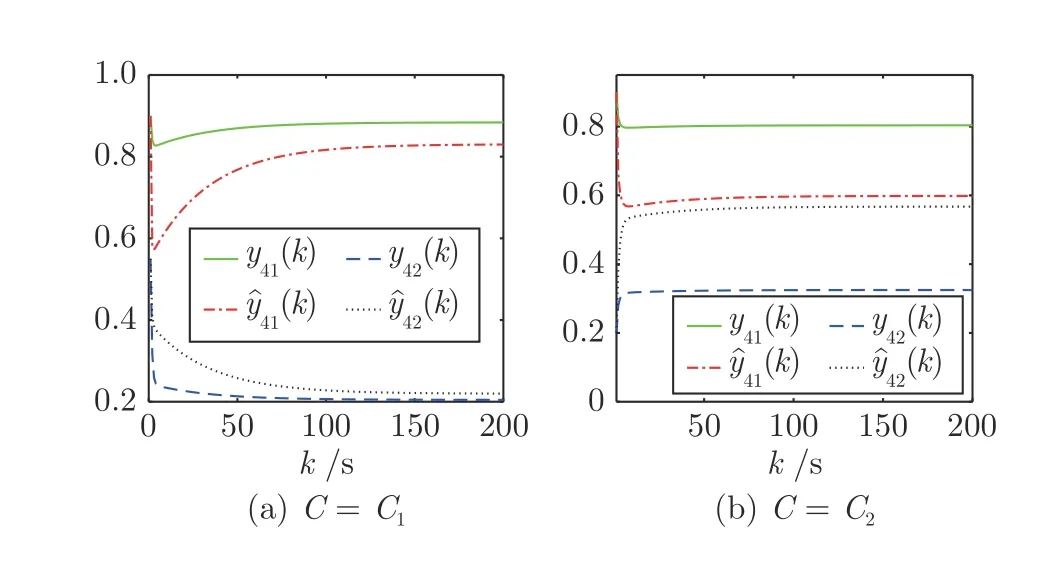
图8 个体4 的观点Fig.8 Opinions of individual 4

进一步地,由图9～11 可知,当C=C1时,遗忘个体5～7 分别对于话题1 和话题2 的私人观点与表达观点非常相近,相对于话题1 和话题2,产生观点两极分化的现象.当C=C2时,针对话题1 和话题2,遗忘个体5～7 的私人观点与表达观点都非常相近,产生观点一致的现象.

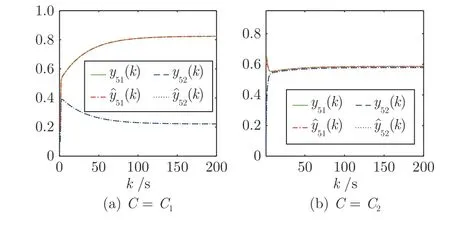
图9 个体5 的观点Fig.9 Opinions of individual 5

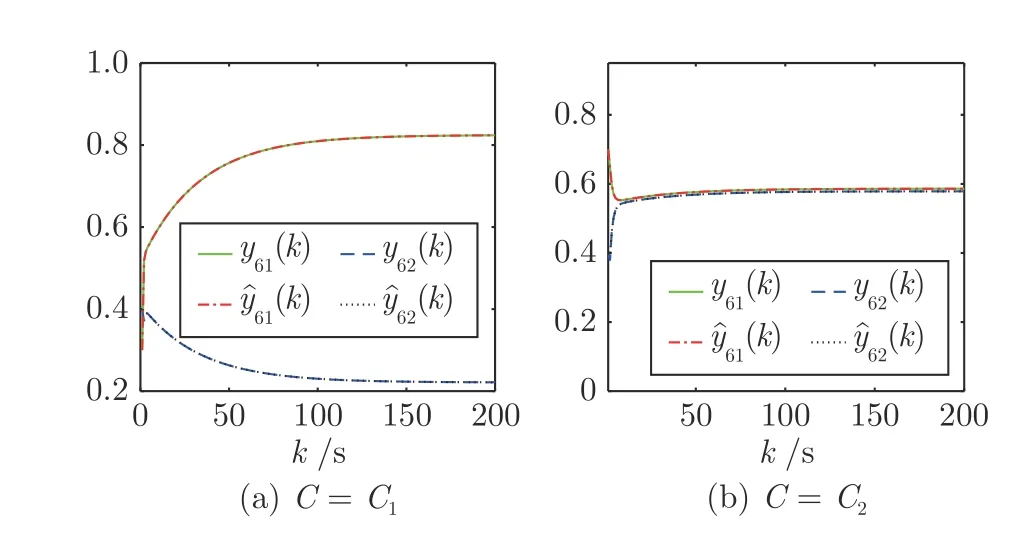
图10 个体6 的观点Fig.10 Opinions of individual 6

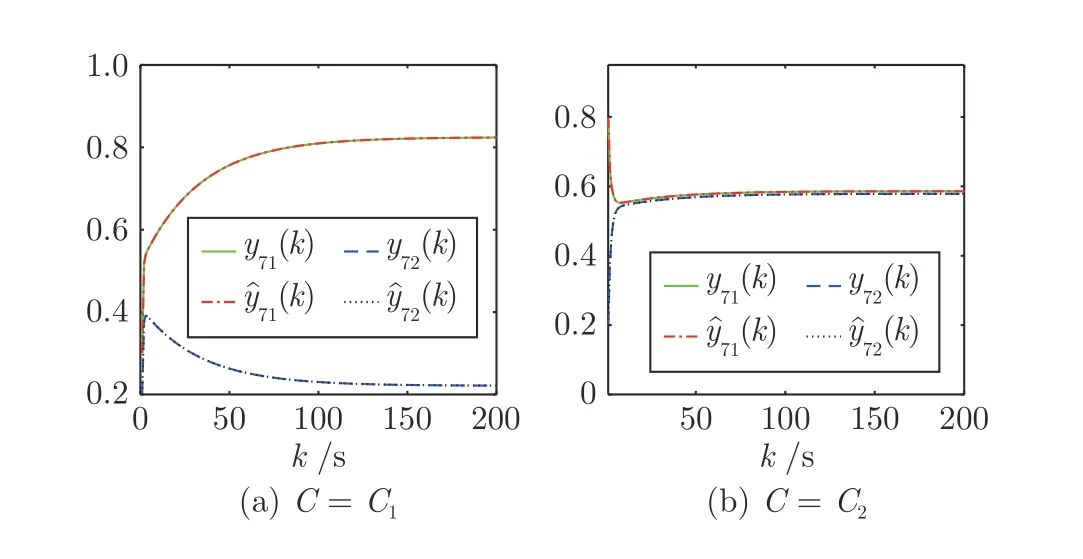
图11 个体7 的观点Fig.11 Opinions of individual 7

为了分析从众压力对于个体表达观点和私人观点差异的影响,设ϕi=0.1,ϕi=0.3,ϕi=0.6,ϕi=0.9 和C=C1.由图12 可知,恢复力参数ϕi越大,个体的私人观点与表达观点越接近.换言之,从众压力越大,个体私人观点与表达观点的差异越大.这与现实世界的经验一致,即个体会因外部环境的影响而适当地改变自己的主观观点.图12 中,不同颜色的线型表示不同个体的表达/私人观点.

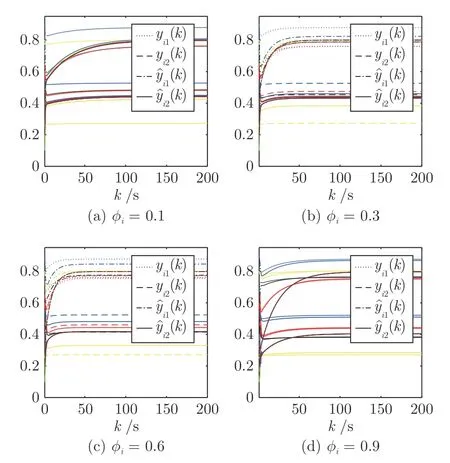
图12 观点动力学模型(17):C=C1Fig.12 Opinion dynamics model (17)withC=C1

5 结束语

本文提出了一个新的具有遗忘个体的多维观点动力学模型,刻画出了不同话题之间表达/私人观点的互相影响.在社会网络是拟强连通的条件下,根据逻辑矩阵和网络影响子矩阵的正则性,给出了表达观点和私人观点收敛的充分条件.应用本文所提出的观点动力学模型,复现了“多元无知”的社会现象.仿真分析表明从众压力的恢复力越小,表达观点与私人观点的差异越大.另外,进一步讨论了逻辑矩阵对表达观点和私人观点演化的影响.

在现实社会中,个体的表达观点在传播和演变过程中,观点传播的速度可能受个体自由意志或者社交媒体的影响.因此,针对观点传播速度的研究是一个值得考虑的问题.这是本文的不足之处.在未来的工作中,一方面,在考虑时间复杂度的基础上,建立连续型的观点动力学社会模型,深入研究观点传播或者演化的速度;另一方面,借鉴探究Bass模型在新领域扩展应用的思想[30]和利用DEA 模型评价优势的思想[31],从一个全新的角度拓展社会网络的应用及说明观点动力学模型具有的优势.