PLVO:基于平面和直线融合的RGB-D 视觉里程计

孙沁璇 苑 晶 张雪波 高远兮

视觉里程计(Visual odometry,VO)在移动机器人定位和导航等任务中发挥着越来越重要的作用[1-4].近年来,高层几何特征,如平面、直线、边缘等,在视觉里程计以及同步定位与建图(Simultaneous localization and mapping,SLAM)中得到了越来越多的关注[5-7].室内环境是移动机器人的重要作业环境之一,由于室内场景属于典型的人造环境,其中存在大量平面、直线等几何结构,能够为机器人定位与建图提供重要的高层环境特征[8-10].与目前最常用的点特征相比[11],高层几何特征对环境纹理缺失以及光照变化有更强的鲁棒性[12-13].另外,几何特征是对原始传感数据的高层参数化表示,能够在尽可能减小数据存储量的前提下保留环境的结构信息,为机器人的自主导航[14]及场景理解[15]提供导航地图和语义描述.

在众多高层几何特征(平面、直线、线段、边缘、轮廓等)中,平面特征具有鲁棒性强、易稳定提取和表示简便等优势,因而在VO 和SLAM 领域得到了较好的应用[16-18].然而,在使用平面参数计算视觉里程计时,常常面临因约束不足而导致的相机位姿求解退化问题[5,19-20].Taguchi 等[19]同时使用点特征和平面特征,给出了可以完全约束相机位姿的特征组合方式,但并没有对只使用平面特征时的退化情况进行具体的分析.Cupec 等[20]在基于平面和线段特征的场景识别中,假设环境包含至少两个非平行平面,此时平面特征对相机位姿估计提供至少5 自由度(Five degree of freedom,5 DoF)约束,使用扩展卡尔曼滤波(Extended Kalman filter,EKF)对该5 DoF 位姿进行估计,之后再利用平面与线段的投票机制对剩余的一个自由度进行计算.然而,由于RGB-D 相机视野范围以及观测距离的限制,会出现难以满足环境包含至少两个非平行平面的假设,如只能观测到平行的桌面和地面的情况.Sun等[5]根据平面特征在三维空间的分布情况,检测出用平面计算位姿时的退化情况,并提出基于STING(Statistical information grid)的扫描匹配方法,对无法被平面约束的位姿自由度进行计算.

除了平面特征外,直线特征也广泛应用于移动机器人室内环境VO 和SLAM[21-24].与平面特征相比,直线特征在室内场景中的数量更多,也更不容易出现退化情况(只要存在两条非平行直线即可完全约束位姿的计算).同时,相比于点特征,直线特征对低纹理环境具有更强的鲁棒性[22-23].然而,通常情况下直线都分布于物体的边缘区域,导致其深度值与RGB 值存在很大的观测噪声[25],因此,直线参数估计的准确性和稳定性不及平面特征.

鉴于上述问题以及平面和直线特征在机器人位姿估计方面的互补性,本文提出基于平面和直线融合的RGB-D 视觉里程计(Plane-line-based RGBD visual odometry,PLVO).首先,针对多几何特征的关联问题,本文对Sun 等[5]提出的平面关联图(Plane association graph,PAG)进行扩展,提出平面-直线混合关联图(Plane-line hybrid association graph,PLHAG),在PAG 的基础上,加入对平面与直线之间几何关系的考虑,实现对两类不同几何特征的统一关联.其次,提出基于平面和直线融合的RGB-D 相机位姿估计方法,在用平面计算位姿出现退化情况时,引入直线特征作为平面特征的补充,通过二者的自适应融合,完成6 DoF 位姿的计算.值得说明的是,由于平面特征参数的准确性和稳定性均优于直线特征,故本文根据平面特征对位姿的约束情况来控制直线特征对位姿求解的贡献,使得直线特征只对平面特征无法约束的自由度进行约束,因此,即使在用平面特征求解时出现退化的情况,也尽可能保证平面特征占主导作用,充分利用平面特征良好的准确性和稳定性,提升位姿估计的效果.

1 PLVO 系统框架

PLVO 系统框架如图1 所示.首先,平面特征提取模块[5]从RGB-D 相机采集的深度图像中提取平面特征,而直线特征提取模块[26]从RGB 图像中检测二维直线,并利用深度信息将其投影到相机坐标系得到三维直线特征.其次,将平面和直线特征输入到平面与直线特征匹配模块中,其中包含两个子模块:PLHAG 构建和PLHAG 匹配.在PLHAG 构建子模块中,对相邻两帧提取的特征分别构建PLHAG,并将其传入PLHAG 匹配子模块完成特征的关联.然后,将具有关联关系的平面和直线特征输入RGB-D 相机位姿估计模块,优先基于平面特征对相机位姿进行计算,当出现退化情况时,用直线特征对平面无法约束的位姿自由度进行计算,最终得到6 DoF 相机位姿的估计结果.

2 特征提取与关联

2.1 平面与直线特征提取

使用基于STING 的平面提取算法[5]对深度图像中的平面特征进行提取,并将提取出的平面的参数表示为π=[nT,d]T,其中,n∈S2表示平面的单位法向量(S2表示三维欧氏空间R3中的单位球面),d∈R表示相机坐标系原点到平面的垂直距离.平面π上的点对应的图像RGB 值的均值和协方差分别表示为rπ和Sπ.

使用LSD (Line segment detector)算法[26]检测RGB 图像中的直线,并将其投影到三维相机坐标系下,得到的三维空间直线参数表示为L=[uT,vT]T,其中,v∈S2表示直线的单位方向向量,而u∈R3的方向为直线与相机坐标系原点构成平面的法向量方向,u的长度为原点到直线的垂直距离.

2.2 平面-直线混合关联图(PLHAG)构建

文献[5]提出了基于PAG 的平面特征关联方法.PAG 是一种全连接图结构,其节点表示平面特征,节点之间的边则代表平面之间的几何关系.相邻帧之间的平面特征匹配是通过比较每帧构建的PAG 之间的节点相似度完成的.本文对PAG 进行扩展,针对多几何特征的关联问题,提出基于PLHAG 的平面和直线混合关联方法.在PLHAG 中,不仅考虑平面之间的几何关系,另外加入了直线与平面之间的几何关系,同时建立平面与平面、直线与直线之间的关联关系.

对于某一帧中提取出的平面集合{πi},i∈{1,···,Nπ}与直线集合{Lj},j∈{1,···,NL},构建的PLHAG 表示为G=(V,E).V表示节点集合,其中包含两类节点类型,即平面节点vπ,i=πi与直线节点vL,j=Lj.相应地,边的集合E也包含两种类型,即平面节点之间的边(Plane-plane edge,PPE)eπ,ik,以及连接直线节点与平面节点的边(Line-plane edge,LPE)eLπ,jk.与PAG 不同的是,PLHAG 不是全连接图结构.考虑到两类几何特征之间的差异,直线节点与直线节点之间不进行连接,具体原因将在第2.3 节中详细说明.

平面节点之间的边eπ,ik定义为

类似地,直线节点与平面节点之间的边eLπ,jk定义为

其中,枚举量ωπ,ik和ωLπ,jk分别表示平面与平面以及直线与平面之间的几何关系类型,即平行关系(parallel)与非平行关系(non-parallel),如式(2)和式(6)所示,在本文实验中阈值δrad取值为10°.由式(3)和式(7)可知,απ,ik为ni与nk之间的夹角,αLπ,jk为vj与nk之间的夹角.根据式(4)和式(8)可知,当两个平面(或直线和平面)之间为平行关系时,dπ,ik(dLπ,jk)的值为两个平行平面(或平行直线与平面)之间的垂直距离.至此,完成PLHAG 的构建,下面将分别使用相邻两帧特征构建的PLHAG 完成平面特征与直线特征的匹配.

2.3 基于PLHAG 的特征匹配

对于从相邻两帧提取的特征集合{πci,Lcj},i∈{1,···,Nπc},j∈{1,···,NLc}和{πrm,Lrp},m∈{1,···,Nπr},p∈{1,···,NLr},其中,下标c与r分别代表当前帧与参考帧,使用第2.2 节提出的方法分别构建PLHAGGc=(Vc,Ec)和Gr=(Vr,Er).在本节中,通过计算Gc中节点与Gr中节点之间的相似度,建立两帧特征之间的匹配关系.

首先,在计算节点相似度之前,分别定义两个PPE 之间和两个LPE 之间的关系,如式(9)和式(10)所示,其中阈值δdist在实验中取值为0.06 m.

满足eπc,ik=eπr,ml关系的两个PPE (满足eLπc,jk=eLπr,pl关系的两个LPE)称为相似边,相似边代表其所连接的两个平面节点(直线节点与平面节点)之间相似的几何关系,用于后文中对节点几何相似度的定义.

接着,对平面和直线节点分别定义节点之间的相似度.两个平面节点vπc,i∈Vc和vπr,m∈Vr之间的相似度sπ(vπc,i,vπr,m)由两部分组成,即颜色相似度sπ,col(vπc,i,vπr,m)与几何相似度sπ,geo(vπc,i,vπr,m).

颜色相似度sπ,col(vπc,i,vπr,m)∈[0,1]为

其中,Sπ=(Sπc,i+Sπr,m)/2.因为具有关联关系的平面特征与其所在扫描帧中其他关联特征之间应具有相同的几何关系.所以,通过以相似边连接的平面节点的颜色相似度计算节点之间的几何相似度sπ,geo(vπc,i,vπr,m),即

其中,Iim为索引对的集合,索引到Vc和Vr中分别与vπc,i和vπr,m以相似边(式(9))连接的平面节点.

而|Iim|则代表集合Iim中元素的个数.

与平面特征不同,直线特征多数分布在几何物体的边缘以及图像中RGB 值变化剧烈的区域,故直线上的点对应像素的颜色信息受观测噪声影响较大,不适合用于对直线特征的描述.因此,本文不计算两个直线节点之间的颜色相似度,只计算其几何相似度,因而在第2.2 节构建的PLHAG 中,直线节点和直线节点之间也不进行连接.

对于两个直线节点vLc,j∈Vc和vLr,p∈Vr,二者之间的相似度sL(vLc,j,vLr,p)定义为

其中,sL,geo(vLc,j,vLr,p)表示直线节点的几何相似度,由以相似边连接的平面节点的颜色相似度计算:

其中,|Ijp|为集合Ijp中元素的个数.

在使用PLHAG 进行特征关联时,根据式(11)和式(16)分别对来自当前帧与参考帧的每一对平面节点之间以及直线节点之间的节点相似度进行计算,通过比较节点相似度的大小来寻找最佳匹配关系,具体算法流程如算法1 所示.

算法 1.基于PLHAG 的特征关联算法

需要说明的是,算法第4 行和第10 行中阈值δs的作用是对不正确的匹配关系进行排除,如对于当前帧中新观测到的特征,参考帧中不存在任何特征与其匹配,这种情况就需要通过对节点相似度数值的限制进行排除.由于关联特征与非关联特征所对应节点的相似度数值的差异比较大,因此,阈值δs的选择对算法结果的影响非常小.本文实验中δs取值为0.99.在图2 中,针对场景中某种具体的特征分布情况,给出了PLHAG 结构的示意图,其中,图2(b)中实线和虚线分别标识了平面和直线节点.对于图2(a)中平面,假设有

其中,η接近1,ε充分小.以节点vLc,1和vLr,1为例,从图2(a)中特征之间位置关系可以看出

则vLc,1和vLr,1所对应的索引集合为I11={(1,1),(2,2),(3,3)},根据式(15)可知

同理可知

根据算法1 可知,{Lc1,Lr1}为一对匹配的直线特征.基于PLHAG 的多特征关联方法利用图结构充分考虑特征之间的几何关系,提高了特征关联的鲁棒性.与PAG 相比,PLHAG 对原单一节点类型进行拓展,将平面和直线特征纳入统一框架,同时考虑了不同特征之间的约束关系,提升了算法的鲁棒性和适用性.

3 RGB-D 相机位姿估计

对于RGB-D 相机,平面特征比直线特征具有更强的稳定性和鲁棒性,因为平面特征多提取于规则几何物体表面,如地面、墙面、桌面等,而直线特征多分布于物体边缘,对应的点云观测噪声显著高于来自规则物体表面的点云观测噪声[25,27].为此,本文主要使用平面特征计算相机位姿.然而,由于RGB-D 相机的观测视野较小,且观测距离有限,导致能够提取出的平面特征数量不够充足,因此,经常出现平面特征无法完全约束6 DoF 相机位姿计算的情况,产生位姿求解的退化问题.针对此问题,本文提出基于平面和直线自适应融合的RGB-D 相机6 DoF 位姿估计方法,在平面特征无法完全提供全部约束时,使用直线特征作为平面特征的补充,完成6 DoF 位姿的计算.

使用第2.2 节中的方法进行特征关联,得到具有关联关系的平面特征集合Π={πci,πri},i∈{1,···,Nπ}以及直线特征集合L={Lcj,Lrj},j∈{1,···,NL}.首先,计算RGB-D 相机的三维空间旋转变换R∈SO(3)和平移变换t∈R3,使得平面特征的匹配误差最小,即目标函数(24)和(25)达到最小.

为了检测是否出现退化解,构造矩阵H=,并计算其奇异值分解 (Singular value decomposition,SVD).

其中,Qr=[qr1,qr2,qr3]和Qc=[qc1,qc2,qc3]为正交单位矩阵,而Λ=diag{λ1,λ2,λ3},λ1≥λ2≥λ3为对角矩阵.根据矩阵H的奇异值,可以判断平面特征是否能够完全约束6 DoF 位姿的计算,具体分为3 种情况,即6 DoF 约束情况、5 DoF 约束情况和3 DoF 约束情况,其中后两种为退化情况.下面分别对这3 种情况给出详细的分析和具体的位姿计算方法.

3.1 6 DoF 约束情况

如果H为非奇异矩阵,即λ1≥λ2≥λ3＞0,则使式(24)和式(25)达到最小值的解分别由式(27)和式(28)得到.

3.2 5 DoF 约束情况

如果H为奇异矩阵,且λ1≥λ2＞λ3=0,此时平面特征的法向量{nci}({nri}),i∈{1,···,Nπ}在空间中是共面关系,且垂直于向量qc3(qr3).在这种情况下,旋转变换为

由此可知,沿着向量qc3方向的平移变换无法被关联的平面特征约束.因此,在计算平移变换的误差函数中加入直线特征的匹配误差,即

其中

此时,使得式(32)最小化的平移最优解为

其中

其中,In为n维单位矩阵.

由式(32)和式(33)可知,直线特征{Lcj,Lrj}对误差函数(32)的贡献量由权值wj进行控制.由式(34)可见,对于t∈/null(Aπ),即在平面特征能提供较强约束的平移方向上,直线特征的权值较小,则其对平移变换求解的贡献也较小;而对于t∈null(Aπ),即在平面特征无法提供约束的平移方向上,直线特征的权值较大,则其对平移变换求解的贡献也较大;当直线方向与qc3垂直时,wj=1,此时直线对平移变换求解的贡献达到最大.图3 给出了一些典型室内场景中平面与直线特征的空间分布,并通过灰度映射的方式反映出每条直线特征的权值大小.从图中可以看出,对qc3方向的平移约束最强的直线,也就是垂直于该方向的直线,其权值最大(图中黑色直线);而对于平行于该方向的直线,其权值最小(图中浅灰色直线).

图3 5 DoF 约束情况下直线权值Fig.3 The weights of lines in 5 DoF constraint cases

总体来说,在平面特征对平移求解约束较强的方向上,尽量使用准确性和稳定性更强的平面参数进行求解,而当产生退化时,再使用直线特征对平面特征无法约束的位姿方向的求解进行补充,实现了两类特征的自适应融合.这样既确保了算法的准确性,同时也有效地解决了使用平面特征求解位姿时出现的退化问题.

3.3 3 DoF 约束情况

如果H为奇异矩阵,且λ1＞λ2=λ3=0,此时平面特征的法向量{nci}({nri}),i∈{1,···,Nπ}在空间中是共线关系,且都沿着向量qc1(qr1)的方向分布.在这种情况下,以qc1为旋转轴的旋转变换无法被平面特征所约束,即在最小化式(24)时存在退化情况.

假设存在旋转变换R1使得两帧平面特征的法向量对齐,即nci=R1nri,∀i∈{1,···,Nπ},而R1与相机真正的旋转变换R之间还相差一个1 DoF旋转,即以qc1为旋转轴的旋转变换R2.在本文方法中,R2是通过直线特征计算的,下文分析直线特征的姿态对计算R2准确性的影响,并基于此给出求解相机旋转变换时,平面与直线特征的自适应融合方法.

考虑任意一对具有匹配关系的直线特征vcj和vrj,假设vrj经过R1变换后为,则由vcj和可以计算R2,即

其中

令ϕ=[0,min{2ϕ,2(π-ϕ)}](〈·,·〉表示向量之间的夹角),如图4 所示,则式(40)可以化简为

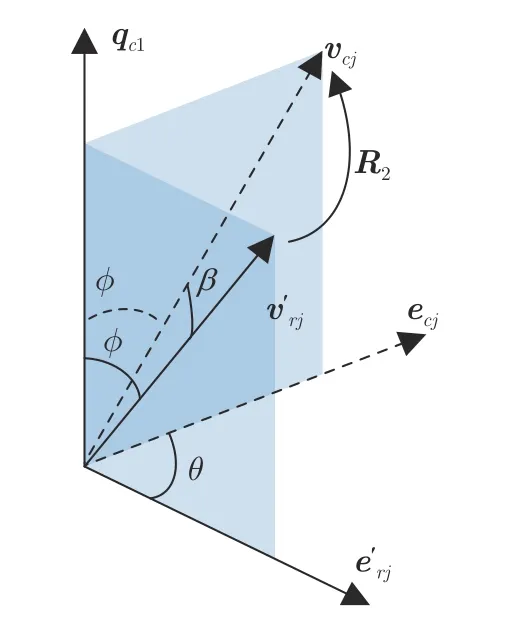
图4 角度θ,β与ϕ示意图Fig.4 Illustration of anglesθ,βandϕ

计算旋转角θ对β的偏导数,可得

图5 给出了在ϕ取不同值的时候,偏导数的曲线.从图5 和式(41)均可以看出,当ϕ=0.5π,即与旋转轴qc1垂直时,θ与β呈线性关系;而ϕ接近0 或π,即与qc1之间接近共线时,β的微小扰动会使得θ剧烈变化,大幅降低旋转角度估计的准确性和稳定性.基于此,在直线特征匹配误差中,通过自适应加权方法调整每个直线特征对求解旋转变换的贡献,即

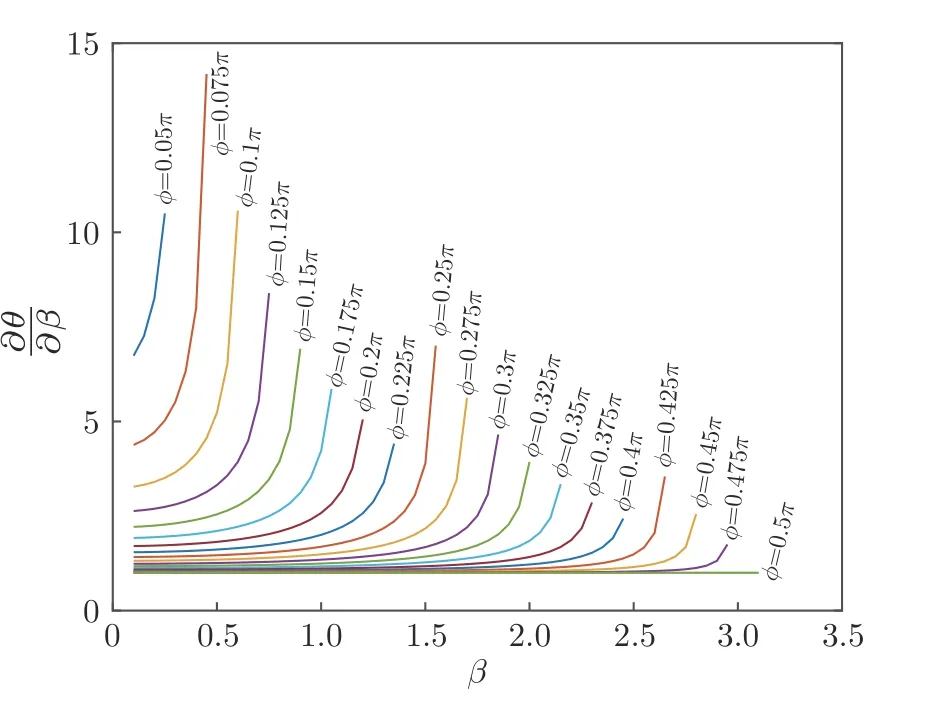
图5 ϕ取不同值时偏导数随β变化曲线Fig.5 Shape of the function w.r.t.βas the value ofϕchanges

其中,权值wRj的计算方法为

其中,QLr=[qLr1,qLr2,qLr3]和QLc=[qLc1,qLc2,qLc3]为正交单位矩阵,而 ΛL=diag{λL1,λL2,λL3},λL1≥λL2≥λL3为对角矩阵.最小化式(43)的最优解可由式(47)进行计算,即

对于平移变换的求解,也无法直接由式(28)得到,而此时矩阵Aπ的零空间为

这种情况下,与5 DoF 约束情况类似,误差函数中加入直线特征的匹配误差,构造为式(32),而平移变换的求解方法也如式(35)所示.与5 DoF约束情况不同的是,权值wj的计算方法由式(34)调整为式(49),即

图6 给出了3 DoF 约束情况的两个场景下平面与直线特征的空间分布,并通过灰度映射的方式反映出每条直线特征的旋转权值wRj以及平移权值wj的大小.从图6(b)可以看出,垂直于qc1方向(即平行于平面)的直线(图中黑色直线)的旋转权值wRj较大,即这些直线对于求解旋转变换的贡献较大;而平行于qc1方向的直线(图中浅灰色直线)的权值wRj较小,即对求解旋转变换的贡献较小.而从图6(c)可以看出,垂直于平面方向的直线(图中黑色直线)的平移权值wj最大,因为这样的直线对于平面特征无法约束的平移自由度,即平行于平面方向的平移的约束是最大的.

图6 3 DoF 约束情况下直线权值Fig.6 The weights of lines in the 3 DoF constraint case

4 实验与分析

本文实验主要分为3 个部分:1)基于PLHAG 的平面-直线特征关联算法验证(第4.1 节);2)不同VO 算法在数据集上的对比实验(第4.2节);3)移动机器人真实环境VO 实验(第4.3 节).实验所用处理器为Intel i7 CPU (1.8 GHz),运行内存8 GB.第4.1 节和第4.2 节实验中所用数据集为TUM RGB-D 公开数据集[28];第4.3 节真实环境实验中所用移动机器人平台为Pioneer 3-DX,传感器为Microsoft Kinect 2.0.

4.1 特征关联实验

为了验证本文提出的基于PLHAG 的平面-直线混合关联算法的有效性,对TUM 数据集中5 个图像序列中的平面与直线特征进行人工标注,并将本文算法与Proença 等[25]提出的视觉里程计(简称为Prob-RGBD-VO)中使用的平面与直线的匹配方法进行比较.本文使用准确率(Precision rate)和召回率(Recall rate)作为特征关联实验的评测指标.其中,准确率定义为被关联算法成功关联并且被人工标注为关联特征的特征数量除以被关联算法成功关联的特征数量.召回率定义为被关联算法成功关联并且被人工标注为关联特征的特征数量除以人工标注为关联特征的特征数量.在实验中,对图像序列中每一帧特征关联结果的准确率和召回率进行计算,并将每个序列上的统计结果以箱线图的形式进行展示,如图7 所示,以此验证特征关联算法的性能.

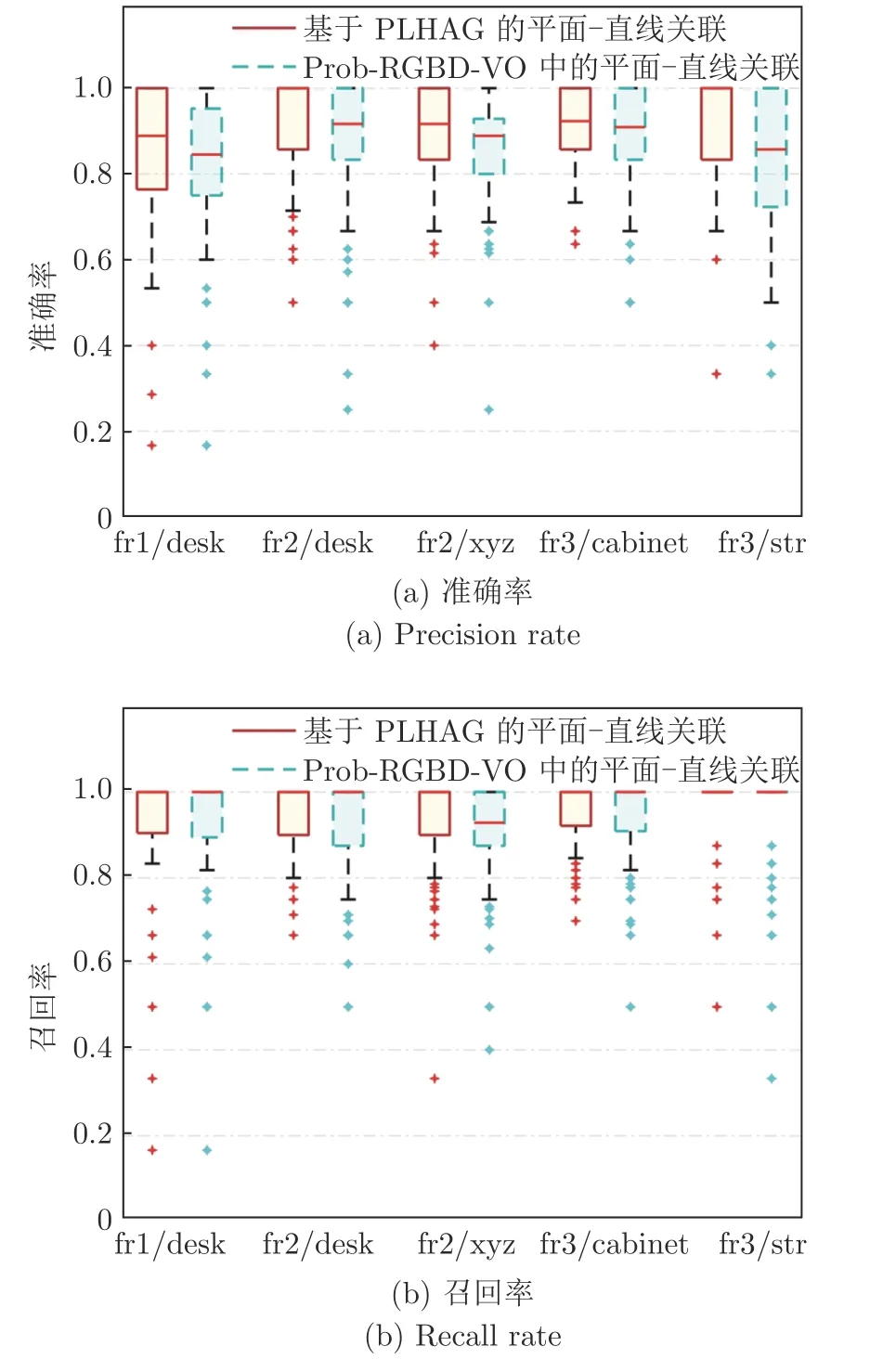
图7 特征关联算法实验结果Fig.7 Comparison of feature association algorithms

在对比算法Prob-RGBD-VO 中,对平面和直线特征分别进行关联.对于平面特征,先利用平面在图像上的重叠区域和几何关系(法向量夹角与截距差)筛选出可能具有匹配关系的候选,接着,对于两个平面π和π′,定义平面到平面的距离为‖dnd′n′‖,然后在匹配候选中选出平面到平面距离最小的匹配对.对于直线特征,首先对图像中提取出的直线特征计算描述子LBD (Line band descriptor)[29],并使用k近邻搜索建立匹配关系,然后保留满足图像2D 直线几何约束(直线方向和截距相似)的匹配对[25].

实验分别使用两种特征关联方法进行相邻帧之间的平面与直线关联,并对其准确率与召回率进行统计.基于PLHAG 的关联方法和Prob-RGBD-VO中所使用的关联方法的平均准确率分别为91.6%和88.9%,平均召回率分别为95.0%和91.7%.由于Prob-RGBD-VO 中关联方法将两类特征分别进行关联,且并未考虑同一扫描帧的特征之间的几何关系,而在PLHAG 中,充分考虑了平面与平面、平面与直线之间的几何关系,进而提高了方法的准确性和鲁棒性.

另外,为了验证算法的时间性能,本文对基于PLHAG 以及PAG 的特征关联算法的对数关联时间分别进行统计,并绘制统计结果的箱线图,如图8(a)所示.需要说明的是,基于PLHAG 的特征关联算法的平均关联时间是0.33 ms,完全满足算法实时性的要求.图8(b)给出的节点数量统计直方图显示了PLHAG 与PAG 中节点数量的差异.可以看到,与基于PAG 的算法相比,PLHAG 由于直线特征的加入使得图结构规模变大,节点数量增加,而在进行特征关联时需要对图结构进行搜索,因此,特征关联过程的运行时间有所增加.尽管如此,从图8(a)可以看出,增加的时间小于1 ms,对VO 系统实时性产生的影响可以忽略不计.

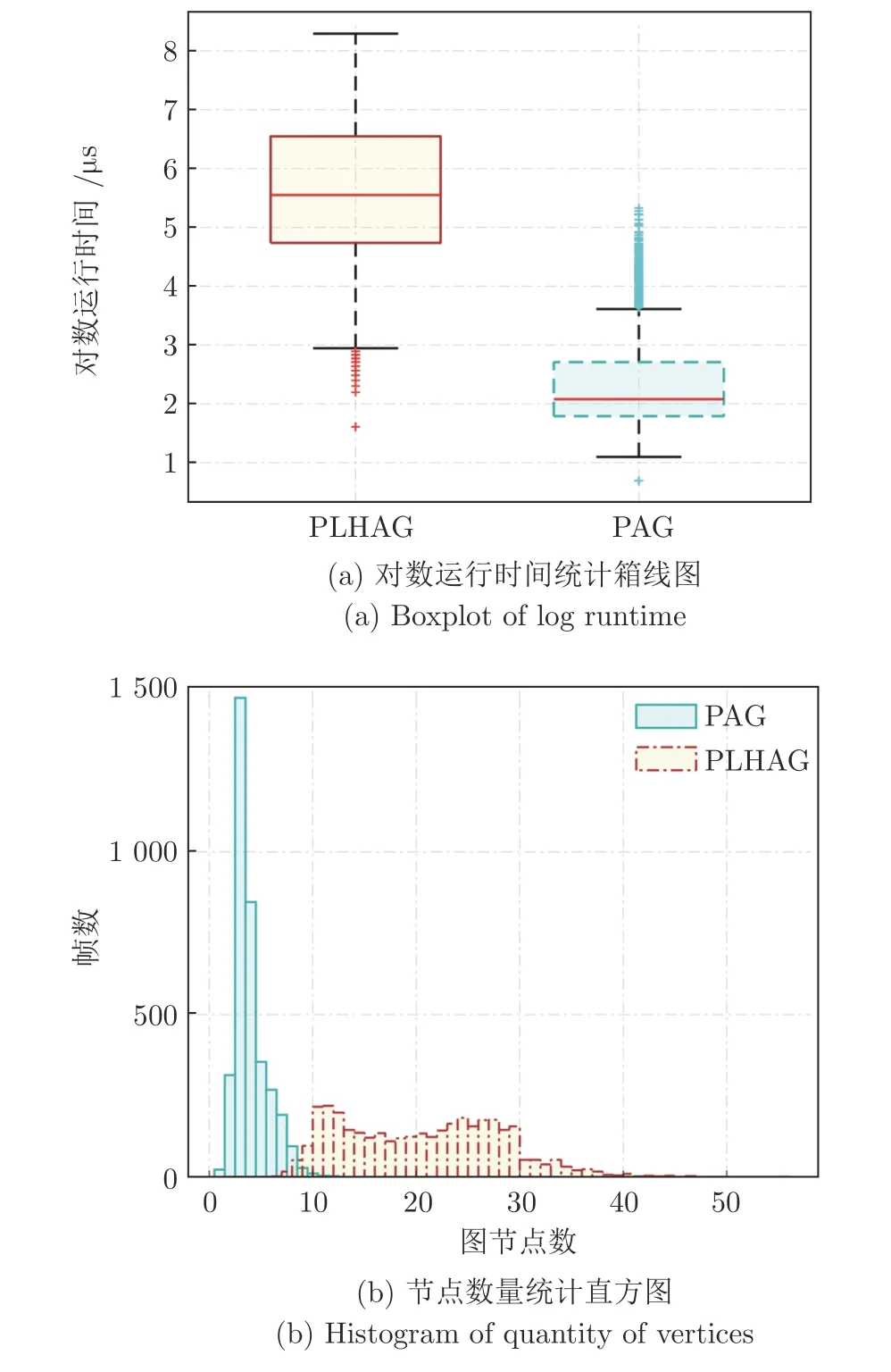
图8 基于PLHAG 与PAG 特征关联方法时间性能对比Fig.8 Comparison of real-time performance for PLHAG and PAG based feature association,respectively

4.2 公开数据集VO 对比实验

在本节实验中,在TUM 数据集5 个场景中运行本文提出的PLVO 算法,并将其结果与4 种VO算法plane-seg-VO[30],Prob-RGBD-VO[25],Canny-VO[31]以及STING-VO[5]进行对比.plane-seg-VO[30]是基于平面与线段特征的RGB-D 视觉里程计,在计算相机位姿时,先利用平面法向量和线段方向向量计算旋转变换,接着通过对齐平面上的点以及线段端点确定平移变换,最后利用迭代最近点(Iterative closest point,ICP)算法对点云进行精确匹配.Prob-RGBD-VO[25]是基于点、直线和平面的RGB-D 视觉里程计,通过3 种特征的联合优化实现对位姿的估计.Canny-VO[31]通过对RGB 图像中提取的Canny 边缘进行扫描匹配,实现视觉里程计的计算.

实验采用的对比性能指标为相对位姿误差(Relative pose error,RPE)和绝对轨迹误差(Absolute trajectory error,ATE),其评测工具分别为TUM 数据集网站提供的python 评测脚本evaluate_ate.py 和evaluate_rpe.py.本文分别对各个算法统计RPE 和ATE 的均方根误差(Root mean square error,RMSE),结果如表1 和表2 所示.为了尽量避免调参不当对4 种对比算法性能的影响,planeseg-VO[30],Prob-RGBD-VO[25]与Canny-VO[31]的结果以及STING-VO[5]在fr2/desk 和fr3/cabinet 上的结果均取自于各自论文公开的实验结果.从表1 和表2 中可以看出,本文提出的PLVO 在绝大多数场景中都能获得最优的准确性,原因在于PLVO利用平面和直线进行位姿估计时,充分利用了两种特征的互补性,即平面特征的准确性和稳定性,以及直线特征克服退化的能力.并且,在PLVO 利用直线特征对平面特征无法约束的位姿自由度进行补充的同时,尽可能地保留平面特征的主导作用,充分发挥平面特征参数提取的准确性和稳定性优势,实现了两类特征的自适应融合.图9 展示了其中三个图像序列的ATE 与RPE 结果评测图,从中可以看出,使用PLVO 计算得到的传感器轨迹与运动捕捉系统获得的真实轨迹有着极高的重合度,RPE 曲线也稳定在较小的范围内,充分证明了本文算法的准确性和鲁棒性.

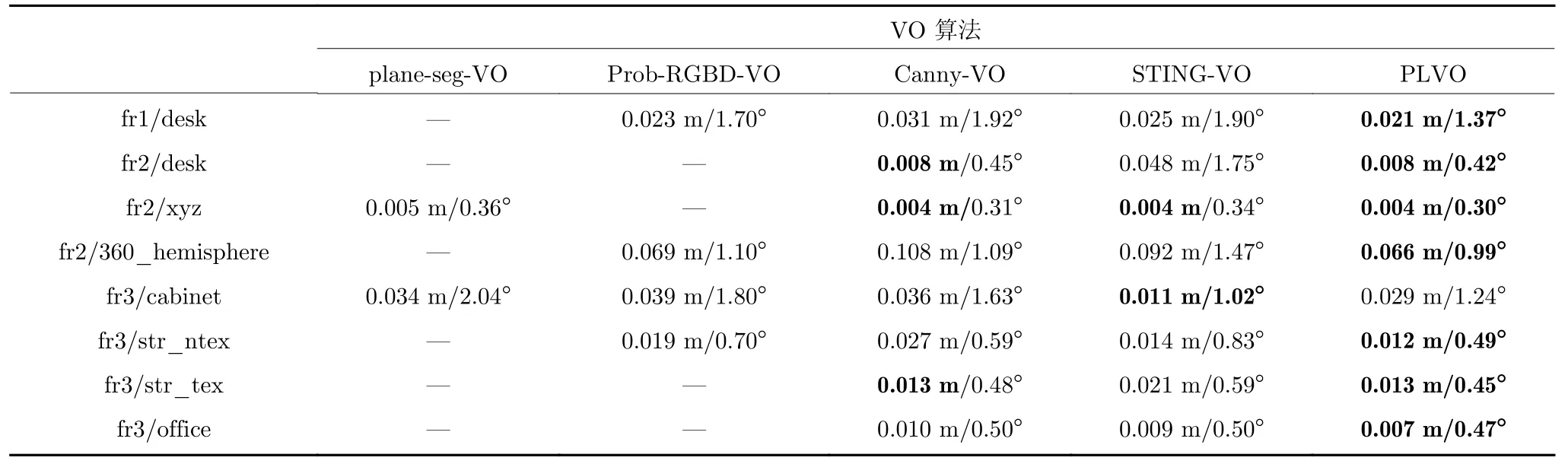
表1 不同VO 算法相对位姿均方根误差对比Table 1 Comparison of RMSE of RPE for different VO methods

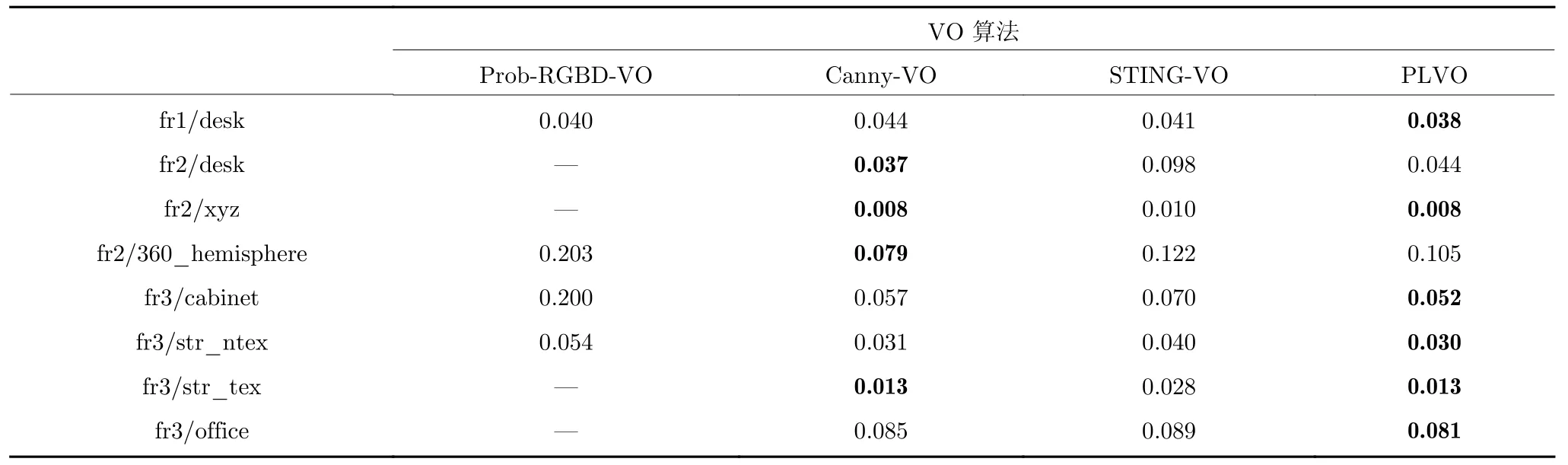
表2 不同VO 算法绝对轨迹均方根误差对比(m)Table 2 Comparison of RMSE of ATE for different VO methods (m)

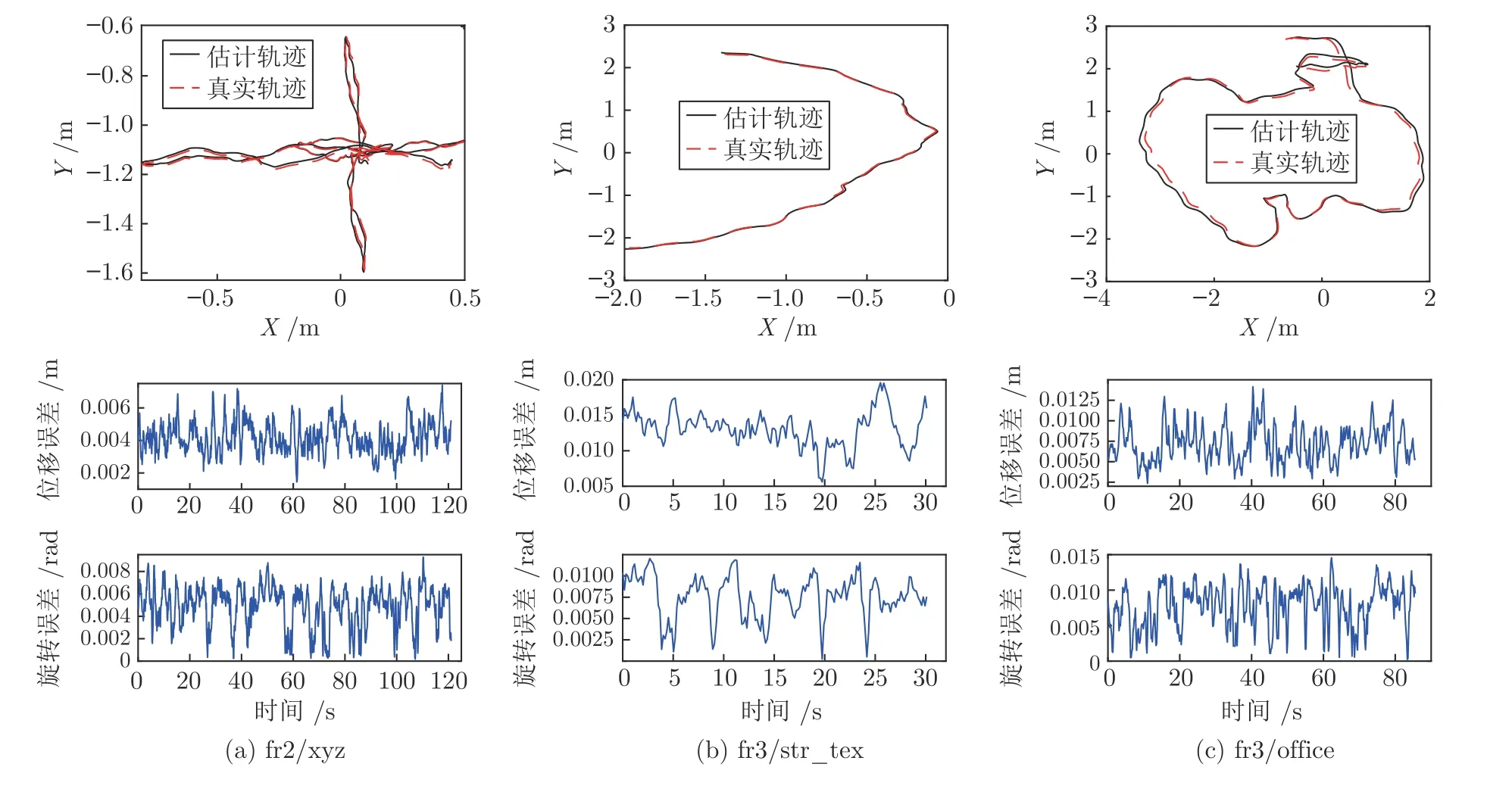
图9 PLVO 算法ATE 和RPE 结果评测图Fig.9 Visualization of ATE and RPE for PLVO

为了更加充分地验证多特征融合在VO 系统中的作用,分别计算基于平面特征的VO (P-VO)、基于直线特征的VO (L-VO)以及基于平面-直线(无自适应加权,即式(33)中wj=1,式(44)中wRj=1 )的VO,统计RPE 指标的RMSE 如表3所示.从表3 中可以明显看出多特征融合以及自适应加权算法对系统准确性的提升作用.需要说明的是,在P-VO 中,会频繁出现位姿求解退化情况,表4 统计了每个图像序列上的求解退化出现次数所占的比例.为了便于对VO 定位精度进行更加客观的比较,在表3 所示的P-VO 的实验结果中,没有统计出现求解退化时的位姿估计结果.而PLVO 中没有出现过退化情况,由此可以看出多特征融合不仅提高了算法的准确性,而且避免了使用单特征的位姿求解算法可能出现的退化问题.

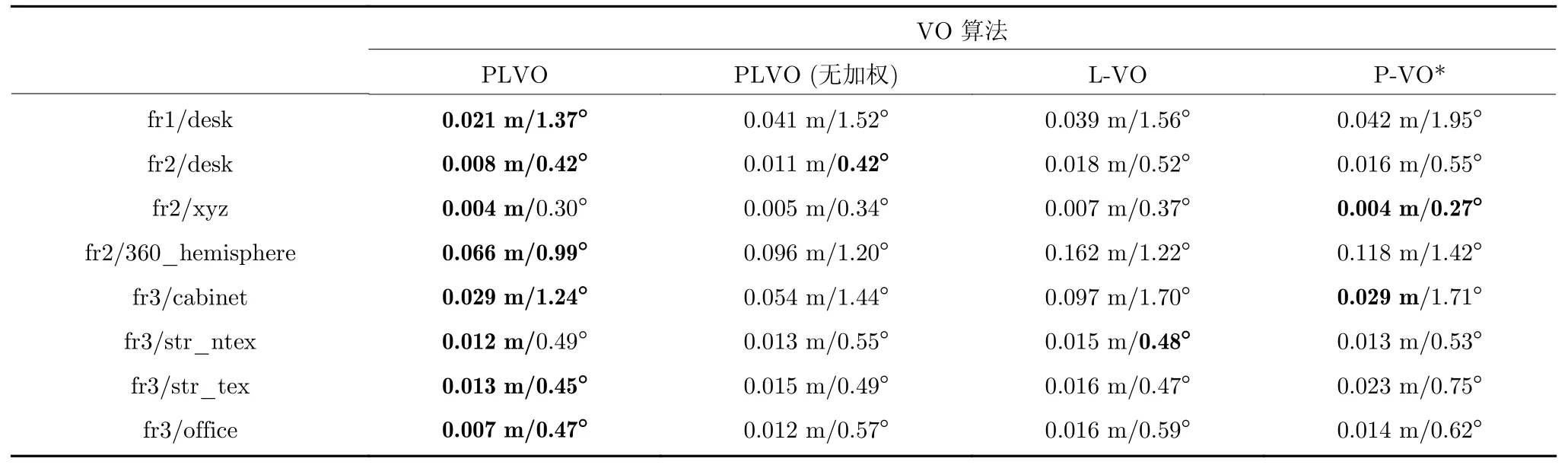
表3 相对位姿均方根误差消融实验结果Table 3 Results of ablation experiment in term of the RMSE of RPE

表4 P-VO 中位姿求解退化情况所占比例Table 4 Ratio of the degenerate cases in P-VO

此外,本文分别对PLVO、P-VO 以及L-VO算法的运行时间进行统计,其箱线图如图10 所示.相比于P-VO 与L-VO 算法,PLVO 算法分别增加了直线提取和平面提取的运行时间,因此实时性略逊于P-VO 与L-VO.尽管如此,PLVO 的帧率仍可达到6～10 Hz,满足系统实时性的要求.

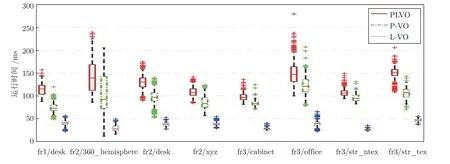
图10 各个图像序列上PLVO、P-VO 以及L-VO 每帧运行时间统计箱线图Fig.10 Boxplot of statistics of the runtime per frame for PLVO,P-VO and L-VO

4.3 室内环境移动机器人VO 实验

为了验证本文算法的有效性,使用PLVO 进行真实环境的移动机器人视觉里程计实验.将Microsoft Kinect 2.0 传感器固定在Pioneer 3-DX 机器人上离地面大约0.34 m 的位置.在实验中,用手柄控制机器人通过一个实验室,环境规模为8.68 m×7.86 m.用PLVO 算法进行机器人的定位与增量式建图,所构建的三维点云地图如图11 所示.图11(a)为俯视全景图,图11(b)和图11(c)给出了在全景图中标注的I,II,III 三处对应的RGB 图像和局部放大的点云地图.从图11 中可以看出,PLVO 在真实室内环境中能够较准确地完成移动机器人的位姿估计.

图11 实验室场景下移动机器人定位与增量式建图结果Fig.11 Real-world experiment in a laboratory using a mobile robot

5 结束语

本文提出了一种基于平面和直线自适应融合的视觉里程计算法.通过对相邻两帧的平面和直线特征统一构建PLHAG,充分考虑了平面与平面、平面与直线之间的几何关系,实现了两类特征的混合关联,提高了多特征关联结果的准确率和召回率.而在估计RGB-D 相机位姿时,充分发挥了平面特征准确、稳定的优点及其在机器人位姿估计中的主导作用.针对平面特征在位姿估计中存在的退化问题,引入直线特征对平面无法约束的自由度进行约束,并设计能够充分体现约束强度的权重,实现了两类特征的主辅相济与自适应融合.多角度的实验验证充分证明了本文提出算法的准确性和有效性.