电梯实验台的陪试电机加载算法研究与仿真

刘成源,韩震宇

(四川大学机械工程学院,四川 成都 610065)

1 引言

直升电梯是一种沿垂直导轨运行的箱体,利用电机进行升降运送人或货物的特种机电设备[1]。由于其密闭的特点,一旦发生事故将会直接对电梯内部人员造成严重伤害。数据调查显示,2020年全国共发生25起电梯事故,因电梯自身故障的7起,共计造成19人伤亡[2],其中大多数事故都是电梯制动器失效而造成的冲顶或蹲底。为了保障使用者的人身安全,对电梯制动器的检测显得尤为重要。

目前对于制动力检测,仍然使用GB 7588—2003《电梯制造与安装安全规范》(下称《规范》)[3]中定义的方法。该方法能够实现对电梯整机制动力的可靠检验,但是对于尚且未安装到电梯井中的制动器无法做出可靠性评价。若使用《规范》中的方法将制动器安装到电梯井中,不仅不便于操作,而且电梯井实验设备造价和维护成本高,不利于整个行业的推广。

由于《规范》中相关标准的缺失,目前对于制动器的独立检测尚且没有形成统一的技术规范。目前赵海宁[4]等提出了对静载荷制动能力性能指标的检测方案与实验设备,该种方案可以实现《规范》中对于静力矩的制动需求,但不能对动态力矩进行检测;而部分商家提供了制动器动态制动实验,可以额外加载惯性力矩,但是测量再控制具有滞后性且力矩的输出存在误差,若根据t0时刻测量结果直接应用到t1而不加以修正,将会带来结果上的偏差;而谢小鹏等[5]和俞声皋[6]等利用制动过程中动能与势能的转化关系,计算需要补偿的能量,填补理论上的缺陷,但在分析过程中直接忽略绳子重量,在面对高层建筑电梯绳子重量占比超过5%时,系统模型出现较大偏差。

为了解决上述文献中存在的问题,本文提出了一种基于能量守恒的陪试电机力矩加载算法,通过分析制动过程的力学规律建立电梯的动力学模型,并利用运行过程中采集的加速度和转矩,计算需要输出的惯性力和额外补偿的转矩,在适当的时候加载到系统中,实现使用电惯量的模拟。仿真表明,相较于现行方法,本算法不仅能够有效模拟真实电梯的运行工况,而且能够在一定范围内缩小力矩的输出误差,具有一定的抗干扰能力。

2 电梯物理学模型建立

常见的曳引式电梯的核心部件由曳引机、轿厢、对重块、导向轮、曳引绳、补偿绳和随行电缆组成[7]。而出于安全性和舒适性的考虑,往往会安装门系统、限位开关和弹簧缓冲器,此类非核心部件并不会显著影响电梯的运行规律,因此在构建物理模型时予以忽略。常见高层居民客用电梯的物理学简化模型如图1所示。

图1 客梯简化模型

3 电梯运行工况分析

电梯完成一次运行任务可简单的使用S型速度曲线进行描述,在启停阶段都可以视为由曳引机控制的加减速运动。根据图1所示的电梯简化模型,假设曳引轮与曳引绳之间不发生相对滑动,对于曳引轮左侧受力情况有

(1)

而曳引轮右侧受力情况有

(2)

式中P为电梯轿厢质量,kg;Q为电梯中的载荷质量,kg;i为曳引比,1;R为曳引轮半径,m;Gw为随行电缆重量,N;Glc为轿厢补偿绳(左补偿绳)重量,N;Gtw为轿顶轮重量,N;Glh为轿厢曳引绳(左曳引绳)重量,N;Grh为对重块曳引绳(右曳引绳)重量,N;Gcwt为对重块重量,N;Grc为对重块补偿绳(右补偿绳)重量,N。其中各部分绳子的重量由式(3)～(7)决定。

Glh=ρ1g(H-x)

(3)

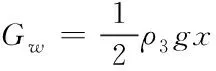
(4)

Glc=ρ2gx

(5)

Grh=ρ1gx

(6)

Grc=ρ2g(H-x)

(7)

其中H为轿厢最大提升高度,m;x为轿厢距地面高度,m;ρi分别为各绳子的线密度,kg·m-1。

当电梯位于不同楼层时,曳引轮两端的偏载力矩由制动器提供的制动力抵消,此时偏载力矩为

M1=(Fl-Fr)R

(8)

代入以上各式有

2iρ1gH-Gcwt-ρ2gH)]R

(9)

当电梯在启停过程中,曳引轮两端会因为系统的加速度而产生额外的惯性力,对于常见的电梯,该部分惯性力是由轿厢、对重、轿厢中的载荷、各绳索的惯性以及各转动部件的转动惯量共同构成。为了方便计算,将惯性折算到某回转体中,由能量守恒定理和刚体转动定理有[8]

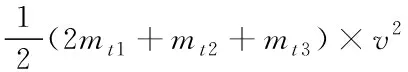
(10)

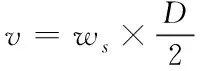
(11)

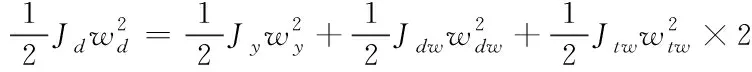
(12)

mt1=ρ1Hi

(13)

mt2=ρ2H

(14)

mt3=ρ3H

(15)

其中Js为直线部分等效后的惯量,kg·m2;mcwt为对重块的质量,kg;ws为等效后飞轮的角速度,rad·s-1;v为电梯轿厢的运行速度,m·s-1;D为曳引轮直径,m;mt1为曳引绳质量,kg;mt2为补偿绳质量,kg;mt3为随行电缆的质量,kg;ρ为绳子线密度,kg·m-1;H为电梯提升高度,m;Jd为回转体的惯量,kg·m-2;wd为回转体的角速度,rad·s-1;Jy、Jdw、Jtw分别为曳引轮、导向轮、轿顶轮的转动惯量,kg·m2;wy、wdw、wtw分别为曳引轮、导向轮、轿顶轮的角速度,rad·s-1。

因此,可得到等效转动惯量为直线部分惯性和转动部分惯量之和,即

(16)

如图1所示的电梯简化模型,对其减速过程进行分析,则惯性力为[8]

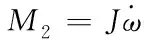
(17)

其中ω为系统曳引轮的角速度,J为系统等效惯量。

那么,对于制动过程中制动力M有

M-M1=M2

(18)

由上述计算可知,制动力矩是以高度x、载重量Q和角速度ω的三元函数。由于补偿绳的存在,使得x前系数接近于0,在电梯系统中可以忽略由于高度不同而产生的力矩变化。考虑到Q和ω为线性叠加关系,对于选取不同常数参数的简化系统,在M1和M2同号取极限时,总力矩可以取得最大值。此时对应着电梯过载下行和空载上行两种极端状态,若制动力不足,电梯极易发生冲顶或墩底,因此需要对两种状态下的制动能力进行判定。

4 制动器制动力检验

4.1 检验设备

如图2所示的是曳引机测试平台的结构示意图,该平台主要由陪试电机、减速器、转矩转速传感器和被测曳引机等构成。使用时由曳引机正常输出转矩,而使用陪试电机模拟输出电梯轿厢、对重和载荷等所带来的偏载转矩和惯性力,在此期间,使用力矩转速传感器实时测量力矩和转速用以反馈[9]。

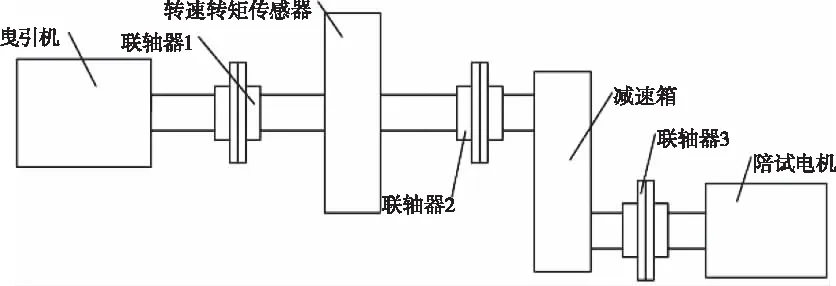
图2 曳引机测试平台

4.2 基于能量守恒的电机驱动方法

根据式(18)可知,减速过程中的制动力由恒定的偏载力矩和与加速度相关的惯性力矩构成,在理论上只需要测量加速度值后,与理论加速度值进行比较便可得到下一时刻陪试电机需要补偿输出的力矩值。但在实际环境中,受制于电压波动、温升和负载波动等影响,偏载力矩的输出无法保持恒定,理论值与实际值也并非相等。因此,需要对两部分转矩之和同时进行修正。

假定在一个电机控制周期内传感器能多次进行采样且控制周期恒定,将整个制动过程划分为n等分且步长为h,那么对于第i个周期的理论转矩Mt(i)有[10]

Mt(i)=M1(i)+M2(i)+T(i)

(19)

其中T(i)为第i个周期内需要补偿的转矩,M2(i)为使用上一个控制周期内角加速度,即

M2(i)=Jαi-1

(20)

若假设第i个周期内实际输出的转矩为Ma(i),则在第i周期内转矩差为

ΔM(i)=Mt(i)-Ma(i)

(21)

可以得到该周期内的能量差为

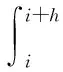
(22)

该能量差需要在下一个周期内进行补偿,为保证总能量守恒有

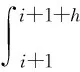
(23)

考虑到在转矩补偿时无法提前获知本周期内的角速度,因此使用上一周期内的角加速度估计本周期内的角速度

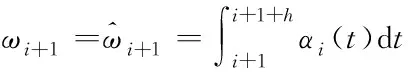
(24)

当控制周期h较小时,可以认为角加速度恒定,使用第i个周期内速度的平均速度替代速度变化,则需要补偿的能量差为

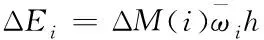
(25)

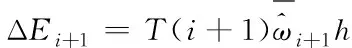
(26)

联立式(25)和(26)则有i+1时刻增加的补偿转矩

(27)

综上,可以得到每个控制周期所需要输出的理论转矩

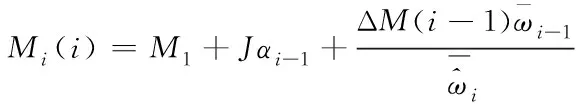
(28)

5 电机加载算法仿真

为了验证该算法的可行性,需要获知电梯在制动过程中的动能变化情况。如图3所示,使用Adams建立电梯物理模型,其中最底端的两轮仅为了方便建立模型且引导补偿绳的走向,并无质量和惯量,而随行电缆质量远小于电梯总质量,在模型中予以忽略。仿真中所使用的电梯模型数据如表1所示。

表1 电梯模型参数

图3 adams仿真模型

使用上述数据模型进行仿真,使载荷为Q的电梯自顶层向下运行,当轿厢运行到额定速度且接近地面时制动器突然抱闸,采集制动过程中各部件的动能,并使用MATLAB处理后可得到系统的总动能如图4所示,系统总动能最大值为4683.05 J。

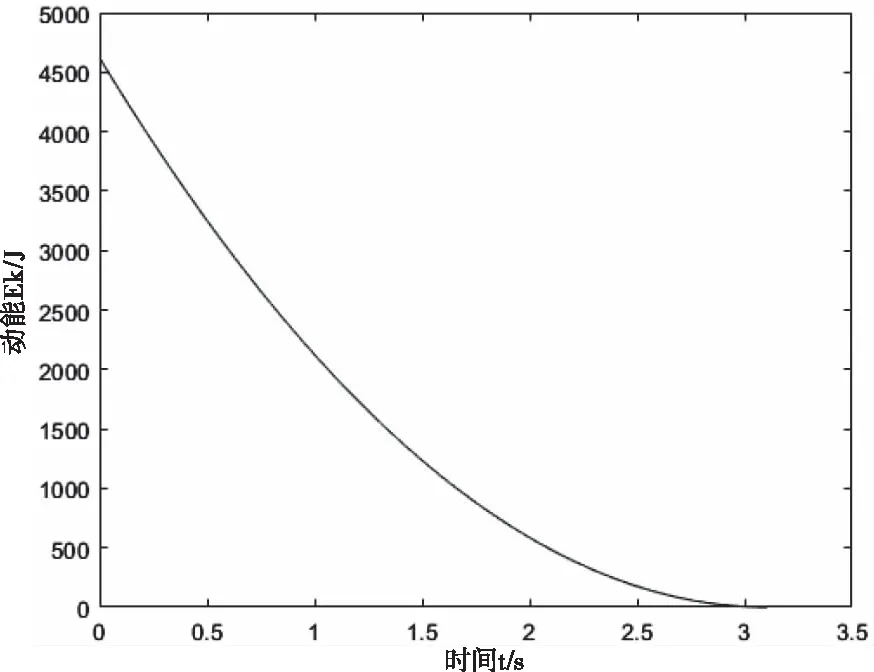
图4 各部件总动能变化情况

基于图2所示的实验台,使用MATLAB模拟制动器减速过程,对整体动能进行仿真检测,验证陪试电机加载算法的可行性。将折算惯量的回转体定为曳引轮(安装到曳引机输出轴上),式(9)和(17)所提到的偏载转矩和惯性力矩由本文提出的电机加载算法控制陪试电机进行输出。假定陪试电机的控制周期为5ms,力矩速度传感器采样频率满足香农采样定理,力矩的实际输出与理论输出存在不超过1%的误差。同时,使用现行商家提供的不补偿的控制方法进行比较,10次仿真结果如表2所示,其中一次的动能变化情况如图5所示。

表2 力矩误差为1%时仿真运行结果

可以看出,使用现行不补偿的方法所输出的能量大小大于理论所需要的动能,最终超出102.64J的能量,而本文的方法超出所需动能84.20J,输出误差为1.80%,力矩模拟的准确性提高17.97%。

将力矩的输出误差增大到5%,进行10次仿真结果如表3所示,其中一次的动能变化如图6所示,现行不补偿的方法超出126.49J,而本方法超出38.09J,输出误差为0.82%,力矩模拟的准确性提高69.88%,本方法依然能够有效的控制输出动能误差。

表3 力矩误差为5%时仿真运行结果

图6 误差为5%时算法动能变化情况

根据两次仿真误差的趋势也可以看出,随着外界干扰的增大,现行检测方法的动能跟随误差在逐渐增大,而本文方法的误差在减小。基于能量守恒方法的陪试电机控制方法在力矩补偿和误差消除方面要优于传统的不补偿方法。

6 结束语

本文通过对电梯的组成结构和运行工况进行分析,得到了制动器在电梯制动过程中所受到的力矩的数学物理模型,针对现行制动力检测方法中存在的力矩输出滞后等问题,提出了一种基于能量守恒的陪试电机力矩补偿算法。在力矩的实际输出环节中加入随机干扰,使用MATLAB对算法进行仿真并与利用Adams得到的电梯运行中的动能变化情况进行对比。仿真表明,与现行不补偿的方法相比,本文提出的加载算法能够有效的降低陪试电机输出能量的误差。但算法在面对较大电机输出误差时,不能完美跟踪理论动能变化,存在制动时间缩短等与实际制动情况不符的现象,需要在未来的研究中不断改进。