基于PLC 技术的家居控制综合系统设计与分析

罗燕杰，柳新枝

（阿克苏地区中等职业技术学校，新疆阿克苏 843000）

0 引言

PLC（Power Line Communication，电力线通信）能够为各种电气设备提供互联网接入[1]，近年来引起了人们的广泛关注，并在智能电网中得到了广泛的应用。随着电力中压通信接入网的飞速发展，宽带PLC 应运而生，现在宽带PLC 的数据速率可以达到约2 Gbps。同时，窄带PLC 被认为是一种很有前途的通信技术的智能家居应用，如电力抄表、电气设备的自动控制以及消费类电器的网络化[2]。

然而，与传统的有线和无线通信相比，由于严重的信号衰落和脉冲噪声，PLC 遇到了更恶劣的环境。通常PLC 信道中的脉冲噪声是随机发生的，持续时间短，功率谱密度高[3]。因此，在脉冲噪声的存在下，PLC 通道的信噪比（Signal to Noise Ratio，SNR）急剧下降。此外，多径效应是导致频率选择性衰落的严重问题，而且PLC 网络是基于分支的拓扑结构[4]。因此，传输的信号在连接的点、电容器组和变压器处反射，从而导致快衰落。在这种情况下对PLC 通道的性能评估，尤其是容量分析，就成为一个至关重要的课题。

本文采用米德尔顿a 类模型对脉冲噪声进行建模，并将PLC 信道建模为记忆信道，利用马尔可夫过程描述带存储器的PLC 通道，推导出可达率、遍历容量和中断概率。

1 PLC 通道及系统模型

1.1 系统通道

本智能家居PLC 基础设施由几个子电路组成，采用单相变压器隔离子电路，具有成本低、体积小的特点，适合智能家居用户使用[5]。这种结构可以为智能家居用户带来安全的用电和方便的维护。系统中有多条平行的电源线用于不同的子电路，因此使用这些电力线同时传输信号，以提高数据速率。此外，由于与变压器的隔离，在不同子电路的电力线上传输的信号不会互相干扰[6]。所以，信号可以通过多个子电路独立地从发射机发送到接收机。本研究设计多样性PLC 子通道对PLC 通道进行建模，发射机和接收机分别使用一个缓冲器来收集发射数据（图1）。

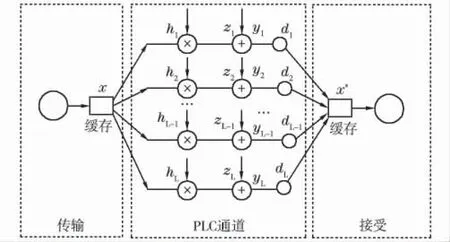
图1 具有L 个分集子信道的PLC 信道模型

此外，采用二进制相移键控（BPSK）来调制通过L 个PLC子信道传输的符号。接收机可以通过从频率、时间和空间组合这些子信道来接收符号。因此，L 个子信道可以被视为一个PLC信道。在PLC 系统中，输入信号通过L 个子信道从发射机传输到接收机。第lth（1≤l≤L）子信道yi为：

其中，xl为通过LTH 子信道传输的信号，zl为子信道的接收噪声，hl为子信道的信道增益。

使用最大比率组合（Maximum Ratio Combining，MRC）将L个子通道组合为一个PLC 通道。从而得到PLC 信道的最优接收信噪比为：

其中，γ 为接收信噪比，wl为第l 个子信道的权值，Ps为发射功率，σ2为信道噪声方差。设wl与第l 个子信道的增益成正比，则接收到的信噪比为：

根据上述方程，组合PLC 信道中的噪声被认为是高斯噪声zg和zw脉冲噪声的组合，即：

1.2 系统模型

PLC 系统目前已广泛应用于建筑物、家庭和企业。在这些地方，电气设备经常打开/关闭，这会产生大量脉冲。此外，变频设备如空调，在转换工作频率时也会产生脉冲。

实际上在PLC 系统中，ION（通电延时定时器）与先前时隙的ION 不独立。以具有恒定数量开关的建筑物为例，当不同数量的这些开关被动态地接通/断开时，会产生不同数量的脉冲。

根据先前时隙中打开/关闭的开关数量，可以预测时隙中开启/关闭的交换机数量。因此，当前时隙的ION 与先前的相关。以图2 中的两个噪声状态作为示例，其中ION 是三次和四次脉冲发生、m 为等于时隙ION 的状态指数。在该系统中，具有非独立离子的脉冲噪声下的PLC 信道可以被视为具有存储器的信道，并且具有有限数量的状态。

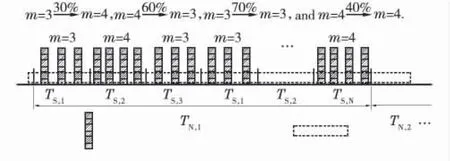
图2 脉冲噪声的发生模式

由于PLC 通道可以被认为是准平稳（或准循环平稳）的，终端节点可以通过使用反馈通道获得CSI（Channel State Information，通道状态信息）。如果一个时隙中的ION 为m（0≤m≤m-1），则使用m 个不同的高斯噪声来近似脉冲噪声。同时将带存储器的PLC 通道建模为具有有限数量状态的非冗余周期性稳定马尔可夫过程（图3）。使用系统状态m 来表示时隙中的ION。

图3 带存储器的PLC 通道的传输信噪比可达率

在马尔可夫过程中，状态集被定义为：

其中，sm表示处于第m 状态的系统，Γ 是换位算子。

在系统中，马尔可夫链是正递归和遍历的。设Un为时隙n处的系统状态，P 为转移概率矩阵。则：

其中，si和sj分别为U 和Pi，j中的状态；0≤i，j≤M-1，表示系统从时隙n 处的第i 状态转移到时隙n+1 处的第j 状态的状态转移概率。

将βm定义为第m 状态的发生概率。用M 状态马尔可夫过程建模的具有存储器的PLC 信道中脉冲噪声的PDF（Probability Density Function，概率密度函数）可以给出为：

其中σ2是第m 状态下噪声的方差。

2 遍历容量和中断概率

为了分析PLC 通道的遍历容量，假定信道增益随所传输符号的不同而不同，并且假定通信时间的持续时间足够长，使信道能够经历所有状态。

根据式（3）和式（4），图2 中PLC 子通道的增益hl服从对数正态分布，其中PDF fhl（x）为：

其中，lnx 是高斯随机变量，μ 和σ2为lnx 的均值和方差。

定义μγ=2μ 和σγ=2σ。那么PDF 可以定义为：

通过式（9），可以将接收SNR 的PDF 近似为：

其中，a0、a1和a2为常数。利用式（10），可以获得接收SNR的CDF：

上述公式给出了带存储器的PLC 信道的遍历容量（以比特/秒/赫兹为单位）的闭合表达式。为了推导带存储器的可编程逻辑控制器信道的遍经容量，假设TN（即N 个输入和输出的持续时间）足够大，以确保能够经历所有系统状态。

式（11）给定具有有限状态数的脉冲噪声下具有存储器的PLC信道，如果CSI 和噪声状态对接收器开放，则遍历容量Cmry为：

停机概率定义为数据速率下降到可接受阈值TR以下的概率，它可作为PLC 系统服务质量的关键度量。具有存储器Pmry的PLC 通道的中断概率为：

其中TD是带存储器的PLC 通道的数据速率阈值。那么式（13）可以写成：

3 数值结果

本文使用MATLAB 获得数值结果，并与解析结果比较，以验证推导过程（表1）。发射信噪比定义为Ps/σ2=10lg（Ps/σ2）。为了模拟PLC 通道，针对不同的槽位产生不同离子的脉冲噪声。为了便于比较，考虑了与不同平均离子相关的3 种情况，分别为A=0.01、A=0.1 和A=0.5。图2 中，PLC 子通道L 的数量为10。此外，通过调整脉冲宽度将Γ 设置为0.01、0.1、0.5 和10。PLC 通道衰落a0、a1、a2的参数分别设置为8.21、12.37、0.02。脉冲噪声和高斯噪声的功率分别设置为-15 dB 和2.5 dB。

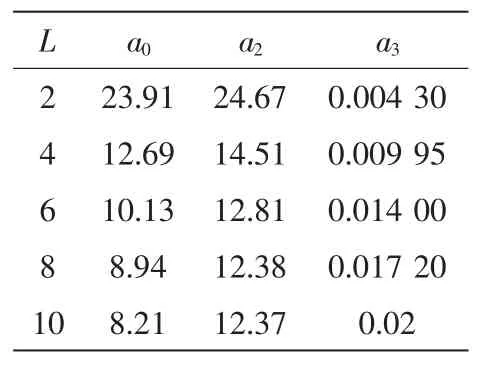
表1 近似参数值推导结果

为了建立仿真环境，使用一个具有3 种噪声状态的PLC 通道。设定ION 分别等于2、6 和10。然后，将这3 种脉冲噪声随机混合，构建轻、中、重3 种脉冲噪声测试环境。在光脉冲噪声环境下，将ION 为2、6、10 的3 种脉冲噪声的比例分别设为94%、5%、1%。在中等脉冲噪声环境下，比例设置为30%、50%、20%。在强脉冲噪声环境下，比例分别设置为1%、5%、94%。最后，3 种环境中的A 分别在0.5、0.1 和0.01 左右。作为基准，同时还考虑了无记忆PLC 信道，其中脉冲噪声的发生遵循泊松分布。为了将所提出的带记忆的PLC 通道与无记忆的PLC 通道进行比较，在光脉冲噪声环境下，将无记忆的PLC 通道的ION、A、L 等参数设置为与带记忆的PLC 通道相同。

根据图3，在给定的3 种测试环境情况下构造一个三态马尔可夫系统，并根据式（6）计算转移概率矩阵。此外，分别推导了ζ 和ρ 值。在有存储器的PLC 通道的输入为高斯信号。然后，使用式（10）得到3 种测试环境下带内存的PLC 通道的可达率（图3）。在光脉冲噪声环境下，存储器PLC 通道的最高可达率。可以观察到在光脉冲噪声环境下，无记忆的PLC 信道的可达率要高于有记忆的PLC 信道。其原因是无记忆PLC 通道的输入输出信号之间的熵比有记忆的PLC 通道的熵大。

为了验证遍历容量，设置参数ωi和qi的值。此外，式（12）计算结果的准确性取决于J。较大的J 可以帮助获得更精确的近似，同时也会导致复杂性的显著增加。因此设定J=10。

图4 为3 种测试环境中带存储器的PLC 通道的遍历容量与发射信噪比的关系。由式（12）得到的分析结果与Monte-Carlo 的结果一致。A 的减小导致遍历容量曲线的差距增大，这是因为轻脉冲噪声状态发生概率的增加导致系统停留在光脉冲噪声状态的时间变长。同样，存在记忆的PLC 通道的遍历容量要比无记忆的PLC 通道大。

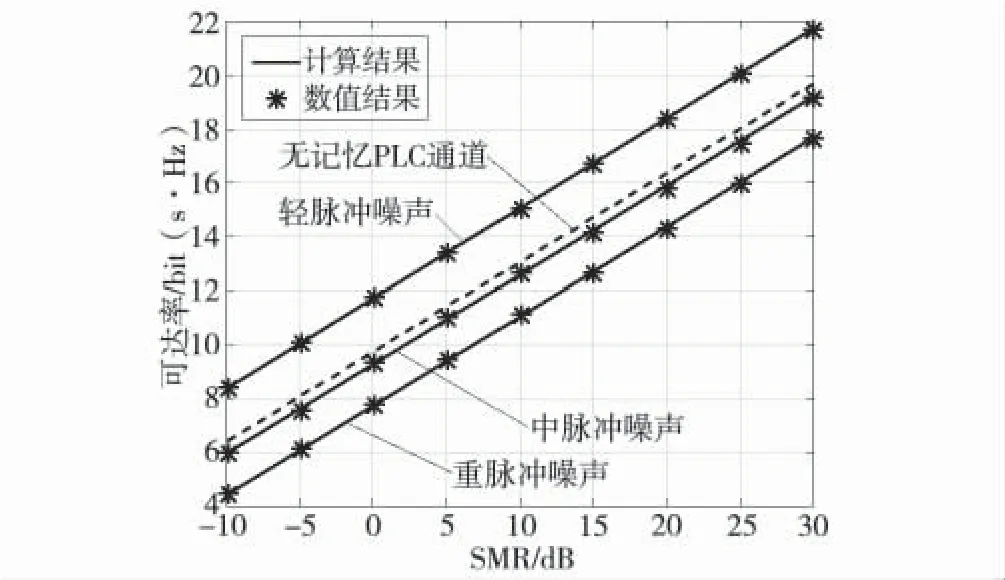
图4 3 种测试环境中带存储器的PLC 通道的遍历容量

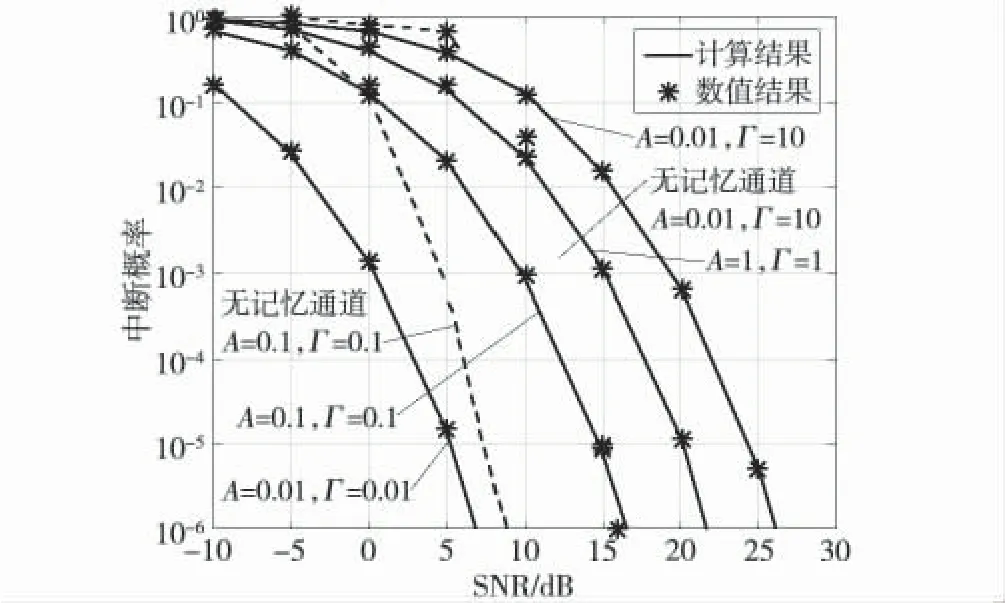
图5 具有不同参数的存储器的PLC 通道的中断概率

图4 为PLC 通道的中断概率与发射信噪比的关系，可以看出分析结果与模拟结果是一致的。随着A 或Γ 的增加，中断概率变得更低。但是，由于Γ 的增加可以显著降低接收信噪比，因此减小Γ 时PLC 系统的中断概率要高得多。同时，即使A 和Γ 相同，无记忆PLC 通道的接收信噪比也要大于有记忆的PLC 通道，因此无记忆PLC 通道的中断概率要优于有记忆的PLC 通道，特别是当Γ 变得非常大（即Γ=10）时，中断概率迅速增加。这是因为较大的Γ 表示脉冲持续时间非常长，导致接收到的信噪比显著降低。

4 结论

本文分析了PLC 系统在脉冲噪声下的性能，将带存储器的PLC 通道建模为马尔可夫过程，通过计算条件状态概率和各状态的可达率，推导出其可达率。通过对对数正态和函数的精确逼近，可以得到接收信噪比的CDF。在CDF 的基础上，给出带存储器的PLC 通道的遍历容量和中断概率的表达式，并用数值结果验证了分析的准确性和正确性。