初中几何运动类题目解题实践

王国鹤

【摘要】几何运动类题目是初中数学的一种常见题目，在中考数学中也常常作为压轴题出现.该类题目有一定的难度，主要考查学生对知识的综合运用能力和逻辑推理能力.学生常常缺乏解题思路，甚至经过一些习题训练后还是无法找到解题的技巧.基于此，文章对几何运动类题目的解题的方法进行归纳和总结，以期帮助学生掌握这类题目的解题方法.

【关键词】几何；运动；作图；技巧；解题实践；初中数学

一、题干中特殊限定条件的标记

几何运动类题目的题干一般较长，问题较多，学生在读题时就应对一些特殊的条件做好标记，避免重复读题或因遗漏一些重要条件导致思考方向不对.

例1 （2019·长春中考）如图1，在Rt△ABC中，∠C=90°，AC=20，BC=15.点P从点A出发，沿AC向终点C运动，同时点Q从点C出发，沿射线CB运动，它们的速度均为每秒5个单位长度，点P到达终点时，P，Q同时停止运动.当点P不与点A，C重合时，过点P作PN⊥AB于点N，连接PQ，以PN，PQ为邻边作？PQMN.设？PQMN与△ABC重叠部分图形的面积为S，点P的运动时间为t秒.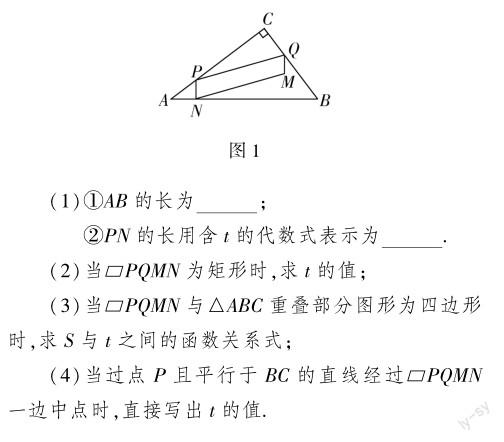

分析 1.这道题目中有两个主动点，其中一个主动点的运动轨迹是较为常见的线段，而另一个主动点Q，它的轨迹是一条“射线”.这里射线的条件就需要做好标记，否则会影响后续的解题.

2.题干中对动点运动开始和结束的限定也要做好标记，这样才能从宏观上了解运动什么时候开始到什么时候结束，时间的取值是否包括运动轨迹的端点及清楚动点结束的位置在哪儿.

3.对于第（3）问中独有的限定的条件：“四边形”同样需要做好标记，这样会时刻提醒学生不要多解.

笔者在这里只对一些特殊的限定条件进行标记，其他的条件学生要学会根据自己的情况，酌情标记.

二、画图的技巧

几何运动类题目的第（1）问常常容易解决，从第（2）问开始就需要学生画图来分析和解答问题，所以学会画图对于解决这类问题是至關重要的.

（一）根据题干中动图的构成方式，再结合主动点及每一问特殊的限定条件进行画图

如例1第二问：这里的？PQMN为动点所形成的动图，它的形成有一定的顺序，首先需要找到主动点P，Q的位置：过点P作PN⊥AB，以PN和PQ为临边做？PQMN.在画图时一定要遵循这样的顺序，这样才可以画出能够用来解题的图.

此题的第二问的特殊限定条件为：？PQMN为矩形.若？PQMN为矩形，那么∠PNM必为90°.此时由∠ANP=90°，得A，N，M三点必然共线，故而可知直线AB和直线MN重合.又因为MN∥PQ，所以此时PQ∥AB.结合上述，便可以按顺序作出第二问的答图（图2）.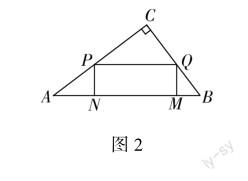

（二）构图时需考虑线段的长短比例关系

在作第二问答图时，应考虑△ABC三边长度为3∶4∶5的直角三角形.而P，Q位置确定有一个重要的条件需要考虑，就是无论运动过程中的何时，AP永远等于CQ.

根据上述的方法以及结合条件的要求，就可以把第三问的二种不同情况的图画出来（图3、图4）.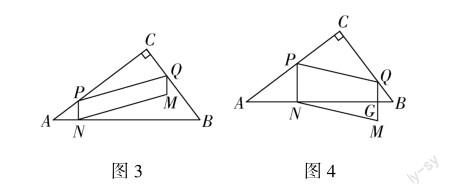

对于第三种重叠方式并不符合第三问“重叠部分为四边形”的要求（图5）.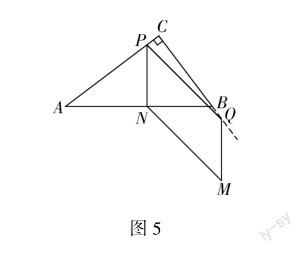

（三）画运动过程中的特定图形时，可用其他问题的图形进行分析，不要过分追求一步成图

根据例1第四问的条件，可得过P点且平行于BC的直线应先过MN的中点，再通过特殊位置图（图2）可以判断当过P点且平行于BC的直线经过MN中点时，点M必在直线AB的下方.故而根据图4，把P点向上、Q点对应的向下移动一点即可出第四问的第一种答图（图6）.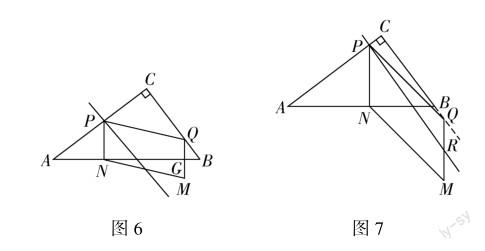

根据图5继续分析可知过P点且平行于BC的直线下一次将经过QM的中点，此时点Q必在B点的下方.故而可画出第四问的第二种答图（图7）.

（四）从动点运动轨迹的重要性

1.如果题干当中出现了“对称点”的条件，我们需考虑从动点的运动轨迹可能是个“圆”.

例2 （2021·长春中考）如图8，在△ABC中，∠C=90°，AB=5，BC=3，点D为AC的中点.动点P从点A出发，沿折线AB-BC以每秒1个单位长度的速度向点C运动，当点P不与点A，C重合时，连接PD.作点A关于直线PD的对称点A′，连接A′D，A′A.设点P的运动时间为t秒.

（2）用含t的代数式表示线段BP的长；

（3）当点A′在△ABC内部时，求t的取值范围；

（4）当∠AA′D与∠B相等时，直接写出t的值.

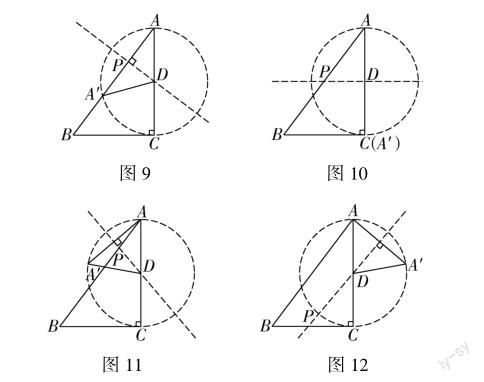
此题中点A′为点P的从动点且是点A关于PD的对称点，根据对称点可知A′D恒等于AD，而点A和点D均为定点，即AD长度在运动过程中为一个定值，所以可以得知A′D长度也为一个定值.依据圆的定义，可以得出A′点的轨迹就是以D为圆心AD的长度为半径的一个圆.画出这道题的第三问和第四问的图就比较简单了（图9、图10、图11、图12）.

三、解題的技巧

几何运动类问题主要考查学生综合知识的运用能力、作图能力、计算能力以及逻辑思维能力.上文提到了审题和作图的一些技巧，接下来，总结归纳一些解题时的技巧.

（一）分析问题用相似的知识，作答时用三角函数的知识

在解几何运动类问题时，可以利用三角形相似来分析问题.用相似三角形的知识可以快速找到图中线段之间的关系，但是用相似三角形作答，答案显得较复杂一些，所以可利用三角函数作答就会使答案变得简单一些.

通过上面的分析，已经知道例1第三问有两种情况，这里只应用第二种情况.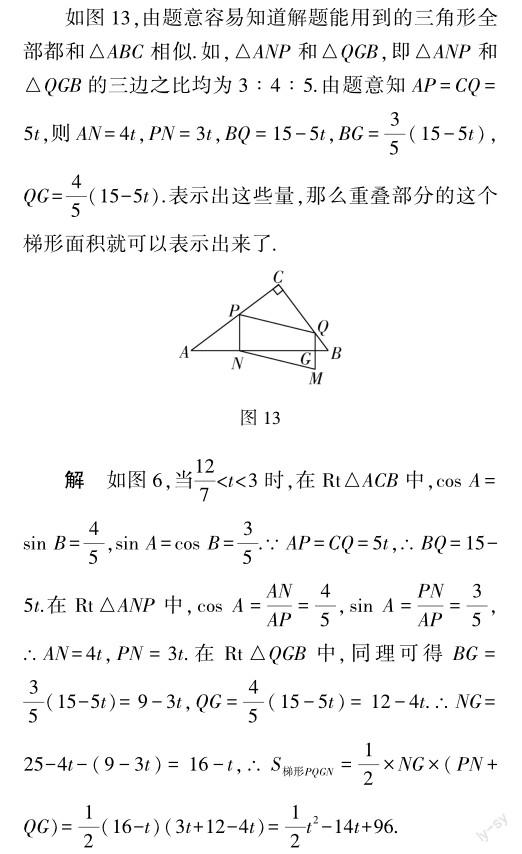

（二）辅助线的构造

辅助线就像桥梁一样，是连接图形与图形，量与量之间的媒介.构造辅助线要依据几何图形的特点，基于作一条线就可以得出很多有用的条件为原则.以例1第四问为例.

这里的中点R是这一问独有的条件，所以中点这一条件必须利用上的.根据几何图形的特点，过R点作RH⊥BN，这样就会出现三角形的中位线（图14）， RH为△NGM的中位线，且△RHK与△ABC相似，从而实现了一线多得的作用.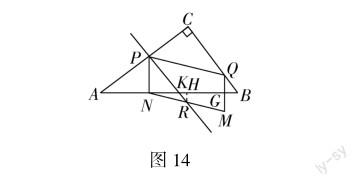

（三）方程思想的应用

方程的发现，是数学的一个历史性飞跃.有许多数学问题很难直接列出算式求解，而方程思想则是用一个未知数来表示问题中的一个量，再通过量与量之间的关系建立一个含有未知数的等式，进而求解.在解决几何运动类问题时，学生经常需要用到方程的思想来求时间t的值.在求解问题时的一条核心思想就是，根据几何关系尽可能多地用含t的代数式去表示一些线段长度，然后再根据线段的和、差、倍、分及比例关系列出含有t的方程，进而求解即可.以例1第四问的一种情况为例.

结 语

几何运动类问题涉及的范围较广，虽然文章提到了一些实用的技巧，但并不代表掌握了这些技巧就可以轻松应对此类题目.学生若想在考场上既快速又准确地做出这类题目，还需要勤加练习，养成逻辑严谨、思维敏捷、计算准确的数学习惯.

【参考文献】

[1]明志芹.方程思想在初中几何中的应用[J].中学生数理化（教与学），2020（08）：85.

[2]黄轶风.运用“中巧说”解决初中几何图形运动问题-以图形的旋转运动为例[J].上海中学数学，2016（04）：20-21，28.

[3]白方.几何变换思想在初中几何教学中渗透与应用研究[D].上海：上海师范大学，2021.